I need your help!

I want your feedback to make the book better for you and other readers. If you find typos, errors, or places where the text may be improved, please let me know. The best ways to provide feedback are by GitHub or hypothes.is annotations.

Opening an issue or submitting a pull request on GitHub: https://github.com/isaactpetersen/Principles-Psychological-Assessment

Adding an annotation using hypothes.is. To add an annotation, select some text and then click the symbol on the pop-up menu. To see the annotations of others, click the symbol in the upper right-hand corner of the page.

Chapter 16 Test Bias

16.1 Overview of Bias

There are multiple definitions of the term “bias” depending on the context. In general, bias is a systematic error (Reynolds & Suzuki, 2012). Mean error is an example of systematic error, and is sometimes called bias. Cognitive biases are systematic errors in thinking, including confirmation bias and hindsight bias. Method biases are a form of systematic error that involve the influence of measurement on a person’s score that is not due to the person’s level on the construct. Method biases include response biases or response styles, including acquiescence and social desirability bias. Attentional bias refers to the tendency to process some types of stimuli more than others.

Sometimes bias is used to refer in particular to systematic error (in measurement, prediction, etc.) as a function of group membership, where test bias refers to the same score having different meaning for different groups. Under this meaning, a test is unbiased if a given test score has the same meaning regardless of group membership. For example, a test is biased if there is differential validity of test scores for groups (e.g., age, education, culture, race, sex). Test bias would exist, for instance, if a test is a less valid predictor for racial minorities or linguistic minorities. Test bias would also exist if scores on the Scholastic Aptitude Test (SAT) under-estimate women’s grades in college, for instance.

There are some known instances of test bias, as described in Section 16.3. Research has not produced much empirical evidence of test bias (Brown et al., 1999; Hall et al., 1999; Jensen, 1980; Kuncel & Hezlett, 2010; Reynolds et al., 2021; Reynolds & Suzuki, 2012; Sackett et al., 2008; Sackett & Wilk, 1994), though some item-level bias is not uncommon. Moreover, where test bias has been observed, it is often small, unclear, and does not always generalize (N. S. Cole, 1981). However, just because there is not much empirical evidence of test bias does not mean that test bias does not exist. Moreover, just because a test does not show bias does not mean that it should be used. Furthermore, just because a test does not show bias does not mean that there are not race-, social class-, and gender-related biases in clinical judgment during the assessment process.

It is also worth pointing out that group differences in scores do not necessarily indicate bias. Group differences in scores could reflect true group differences in the construct. For instance, women have better verbal abilities, on average, compared to men. So, if women’s scores on a verbal ability test are higher on average than men’s scores, this would not be sufficient evidence for bias.

There are two broad categories of test bias:

1. predictive bias
2. test structure bias

Predictive bias refers to differences between groups in the relation between the test and criterion. As with all criterion-related validity tests, the findings depend on the strength and quality of the criterion. Test structure bias refers to differences in the internal test characteristics across groups.

16.2 Ways to Investigate/Detect Test Bias

16.2.1 Predictive Bias

Predictive bias exists when differences emerge between groups in terms of predictive validity to a criterion. It is assessed by using a regression line looking at the association between test score and job performance. For instance, consider a 2x2 confusion matrix used for the standard prediction problem. A confusion matrix for whom to select for a job is depicted in Figure 16.1.

Figure 16.1: 2x2 Confusion Matrix for Job Selection. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

We can also visualize the confusion matrix in terms of a scatterplot of the test scores (i.e., predicted job performance) and the “truth” scores (i.e., actual job performance), as depicted in Figure 16.2. The predictor (test score) is on the x-axis. The criterion (job performance) is on the y-axis. The quadrants reflect the cutoffs (i.e., thresholds) imposed from the 2x2 confusion matrix. The vertical line reflects the cutoff for selecting someone for a job. The horizontal line reflects the cutoff for good job performance (i.e., people who should have been selected for the job).

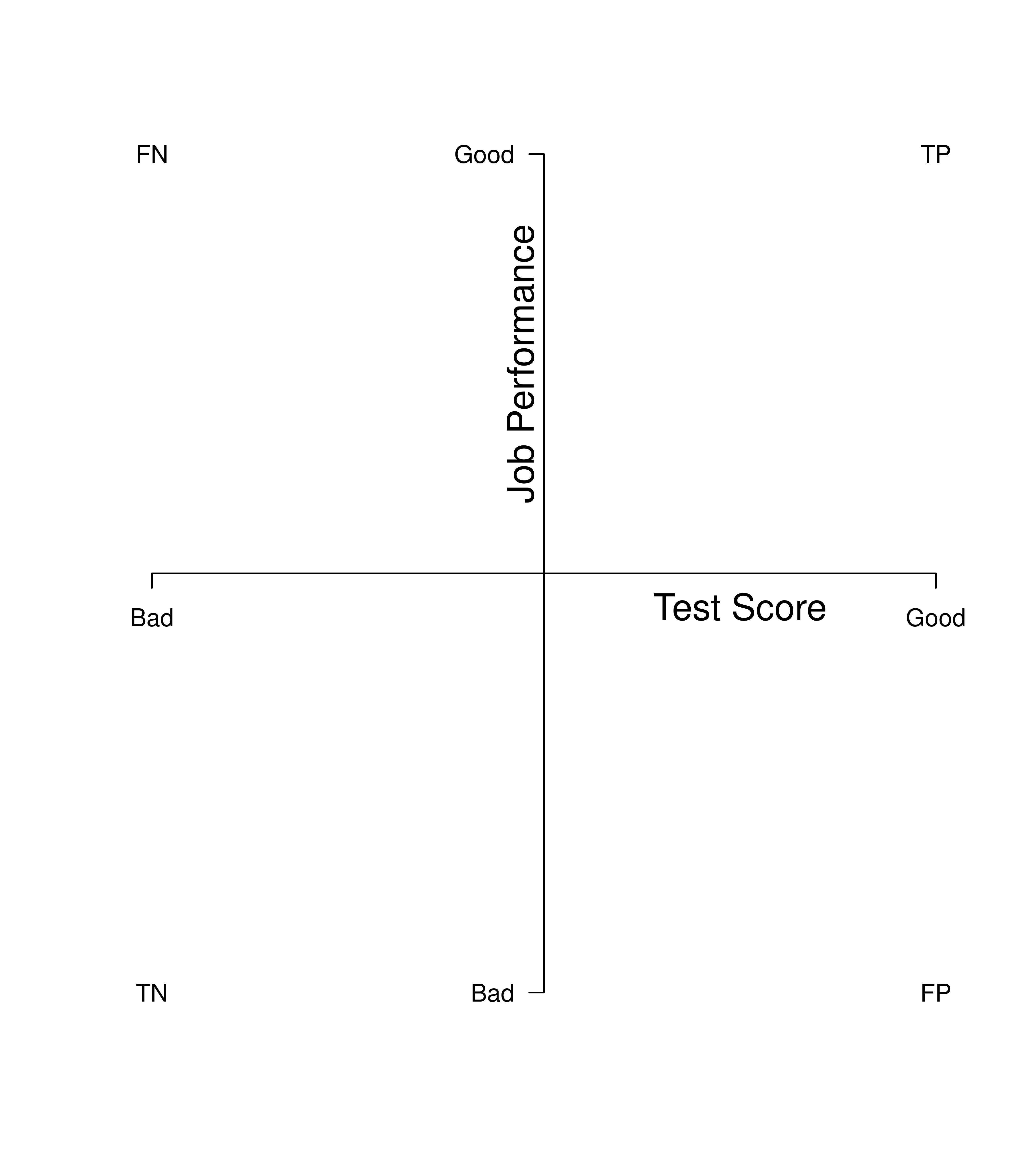
Figure 16.2: 2x2 Confusion Matrix for Job Selection in the Form of a Graph With Predicted Performance on the x-Axis and Actual Job Performance on the y-Axis. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

The data points in the top right quadrant are true positives: people who the test predicted would do a good job and who did a good job. The data points in the bottom left quadrant are true negatives: people who the test predicted would do a poor job and who would have done a poor job. The data points in the bottom right quadrant are false positives: people who the test predicted would do a good job and who did a poor job. The data points in the top left quadrant are false negatives: people who the test predicted would do a poor job and who would have done a good job.

Figure 16.3 depicts a strong predictor. The best-fit regression line has a steep slope where there are lots of data points that are true positives and true negatives, with relatively few false positives and false negatives.

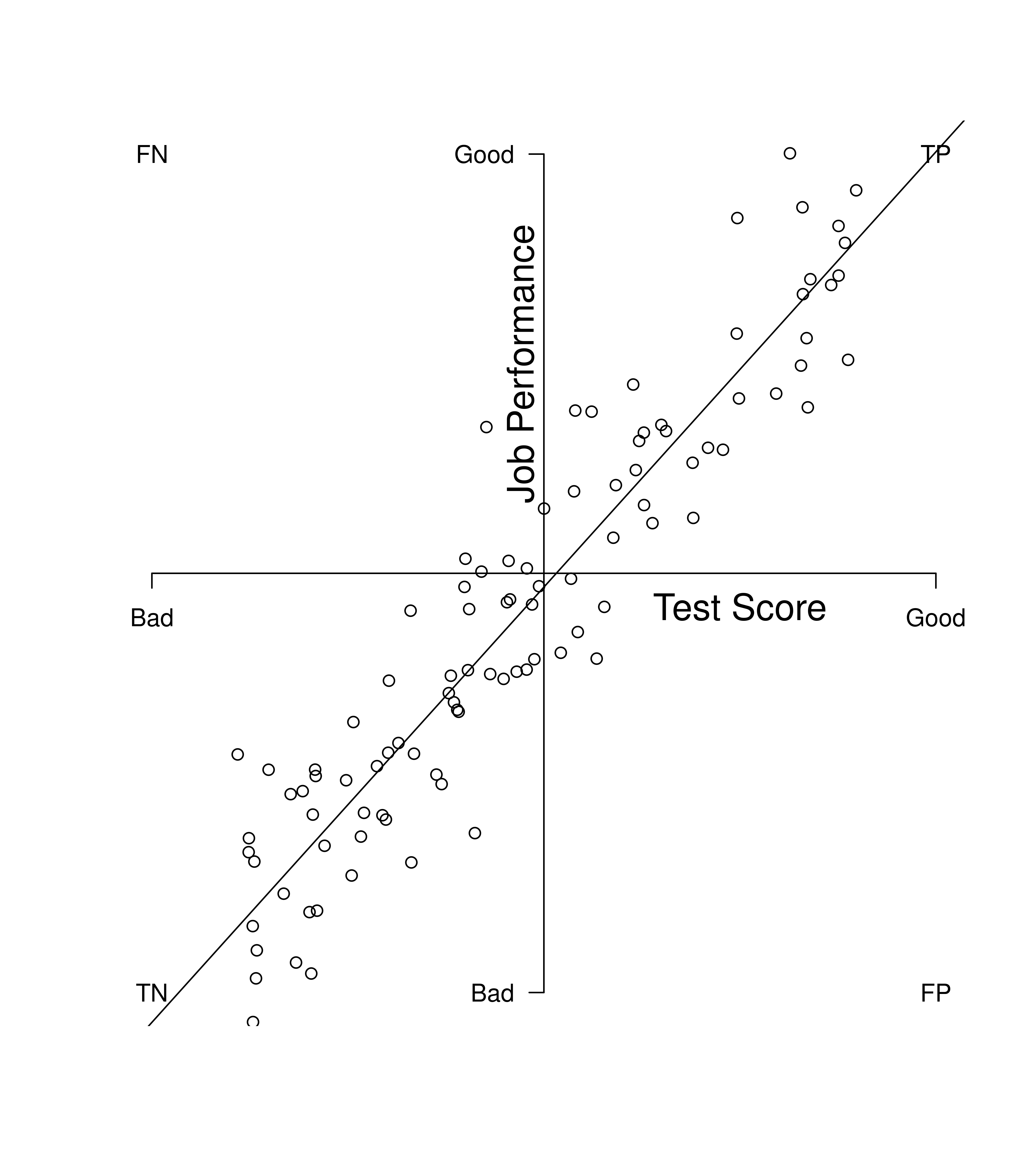
Figure 16.3: Example of a Strong Predictor. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

Figure 16.4 depicts a poor predictor. The best-fit regression line has a shallow slope where there are just as many data points that are in the false cells (false positives and false negatives) as there are in the true cells (true positives and true negatives). In general, the steeper the slope, the better the predictor.

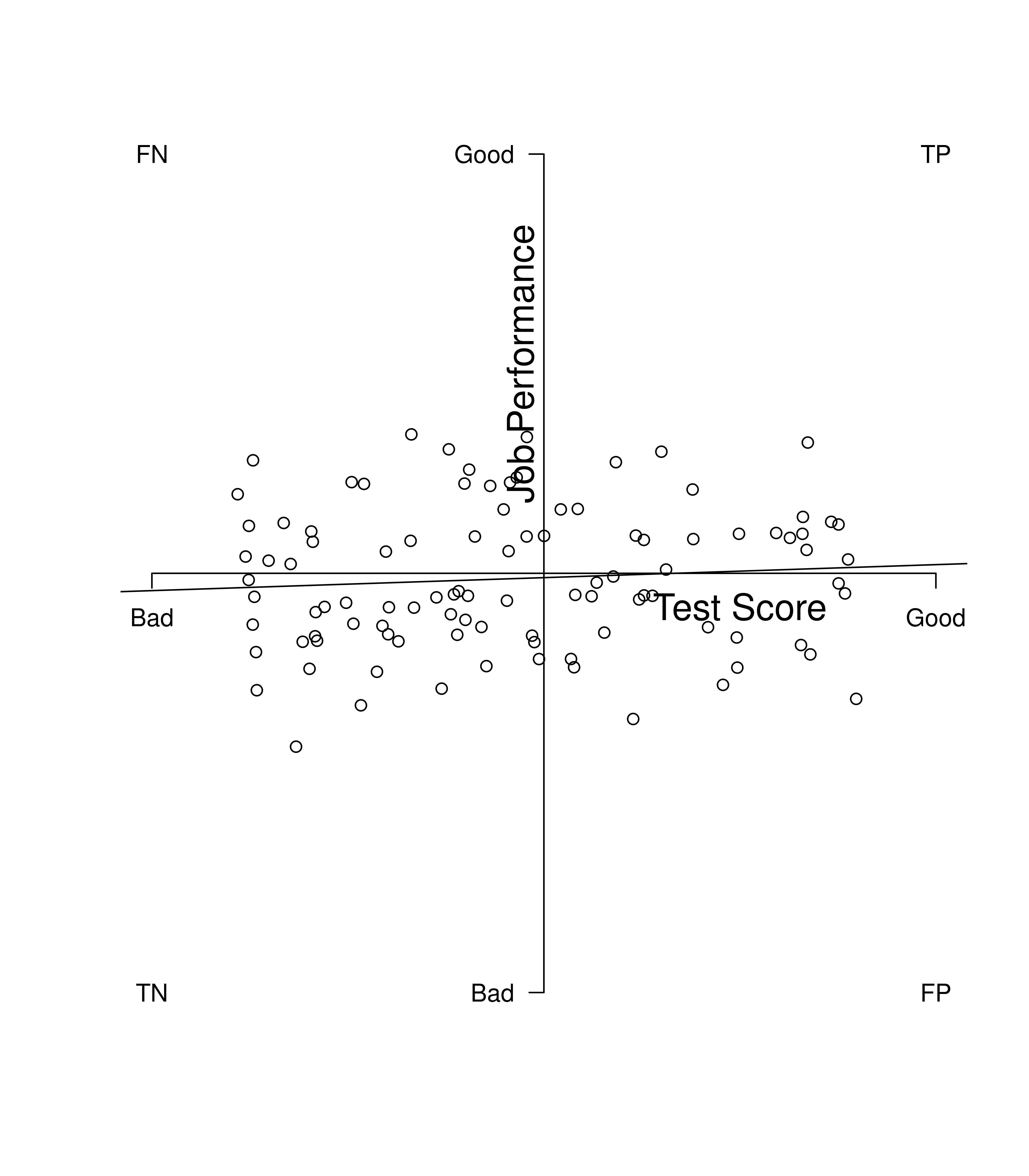
Figure 16.4: Example of a Poor Predictor. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

We can evaluate predictive bias using a best-fit regression line between the predictor and criterion for each group.

16.2.1.1 Types of Predictive Bias

There are three types of predictive bias:

1. Different slopes
2. Different intercepts
3. Different intercepts and slopes

The slope of the regression line is the steepness of the line. The intercept of the regression line is the y-value of the point where the line crosses the y-axis (i.e., when \(x = 0\)). If a measure shows predictive test bias, when looking at the regression line for each group, the groups’ regression lines differ in either slopes and/or intercepts.

16.2.1.1.1 Different Slopes

Predictive bias in terms of different slopes exists when there are differences in the slope of the regression line between minority and majority groups. The slope describes the direction and steepness of the regression line. The slope of a regression line is the amount of change in \(y\) for every unit change in \(x\) (i.e., rise over run). Differing slopes indicate differential predictive validity, in which the test is a more effective predictor of performance in one group over the other. Different slopes predictive bias is depicted in Figure 16.5. In the figure, the predictor performs well in the majority group. However, the slope is close to zero in the minority group, indicating that there is no association between the predictor and the criterion for the minority group.

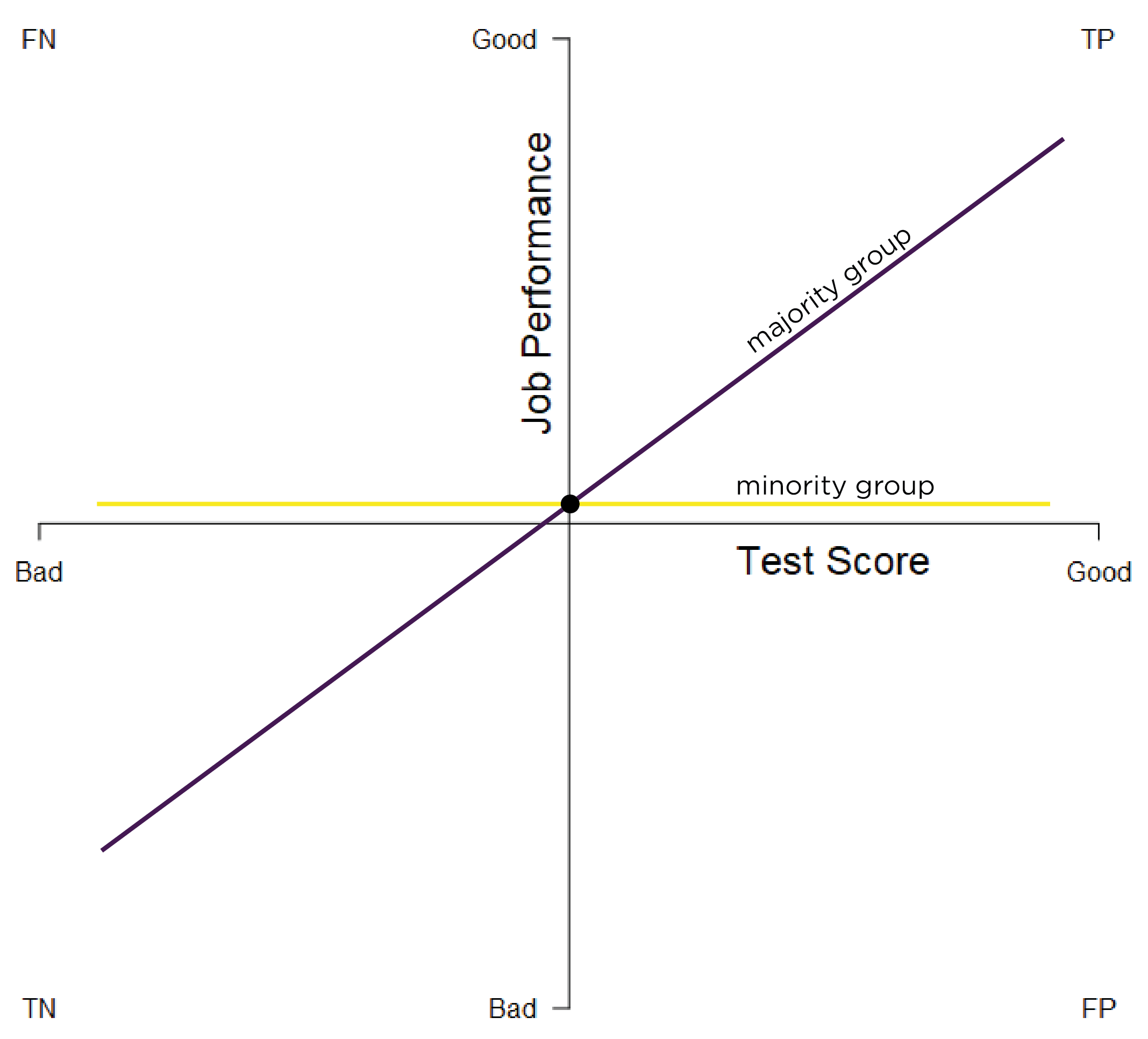
Figure 16.5: Test Bias: Different Slopes. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

Different slopes can especially occur if we develop our measure and criterion based on the normative majority group. Not much evidence has found empirical evidence of different slopes across groups. However, samples often do not have the power to detect differing slopes (Aguinis et al., 2010). Theoretically, to fix biases related to different slopes, you should find another measure that is more predictive for the minority group. If the predictor is a strong predictor in both groups but shows slight differences in the slope, within-group norming could be used.

16.2.1.1.2 Different Intercepts

Predictive bias in terms of different intercepts exists when there are differences in the intercept of the regression line between minority and majority groups. The \(y\)-intercept describes the point on the \(y\)-axis that the line intersects with the \(y\)-axis (when \(x = 0\)). When the distributions have similar slopes, intercept differences suggest that the measure systematically under- or over-estimates group performance relative to the person’s ability. The same test score leads to systematically different predictions for the majority and minority groups. In other words, minority group members get different tests scores than majority group members with the same ability. Different intercepts predictive bias is depicted in Figure 16.6.

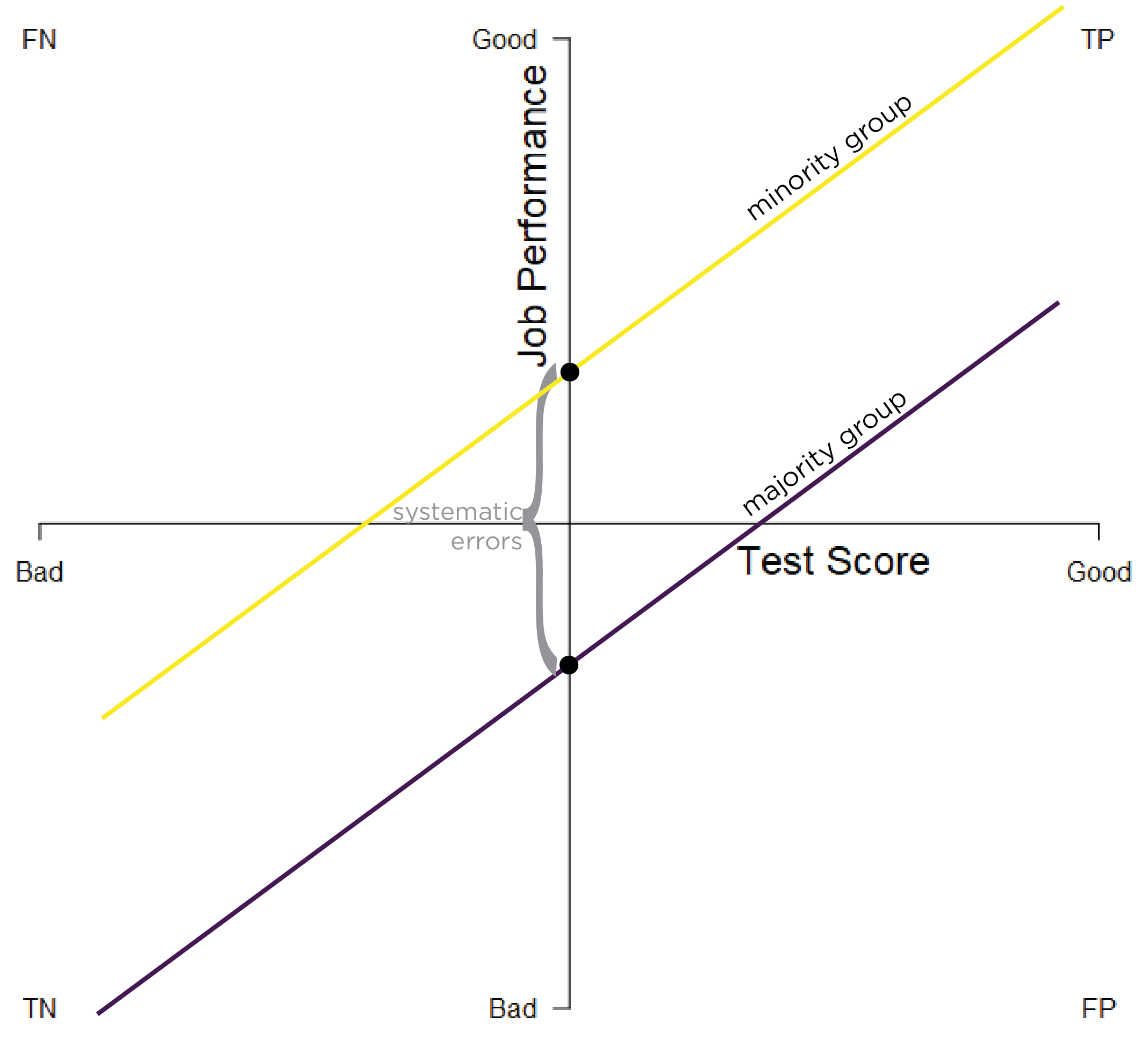
Figure 16.6: Test Bias: Different Intercepts. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

A higher intercept (relative to zero) indicates that the measure under-estimates a person’s ability (at that test score)—i.e., the person’s job performance is better than what the test score would suggest. A lower intercept (relative to zero) indicates that the measure over-estimates a person’s ability (at that test score)—i.e., the person’s job performance is worse than what the test score would suggest. Figure 16.6 indicates that the measure systematically under-estimates the job performance of the minority group.

Performance among members of a minority group could be under- or over-estimated. For example, historically, women’s grades in math and engineering classes tended to be under-estimated by the Scholastic Aptitude Test [SAT; M. J. Clark & Grandy (1984)]. However, where intercept differences have been observed, measures often show small over-estimation of school and job performance among minority groups (Reynolds & Suzuki, 2012). For example, women’s physical strength and endurance is over-estimated based on physical ability tests (Sackett & Wilk, 1994). In addition, over-estimation of African Americans’ and Hispanics’ school and job performance has been observed based on cognitive ability tests (N. S. Cole, 1981; Reynolds & Suzuki, 2012; Sackett et al., 2008; Sackett & Wilk, 1994). At the same time, the Black–White difference in job performance is less than the Black–White difference in test performance.

The over-prediction of lower-scoring groups is likely mostly an artifact of measurement error (L. S. Gottfredson, 1994). The over-estimation of African Americans’ and Hispanics’ school and job performance may be due to measurement error in the tests. Moreover, test scores explain only a portion of the variation in job performance. Black people are far less disadvantaged on the noncognitive determinants of job performance than on the cognitive ones. Nevertheless, the over-estimation that has been often observed is on average—the performance is not over-estimated for all individuals of the groups even if there is an average over-estimation effect. In addition, simulation findings indicate that lower intercepts (i.e., over-estimation) among minority groups compared to majority groups could be observed if there are different slopes but not different intercepts in the population, because different slopes are likely to go undetected due to low power (Aguinis et al., 2010). That is, if a test shows weaker validity for a minority group than the majority group, it could appear as different intercepts that favor the minority group when, in fact, it reflects shallower slopes of the minority group that go undetected.

Predictive biases in intercepts could especially occur if we develop tests that are based on the majority group, and the items assess constructs other than the construct of interest which are systematically biased in favor of the majority group or against the minority group. Arguments about reduced power to detect differences are less relevant for intercepts and means than for slopes.

To correct for a bias in intercepts, we could add bonus points to the scores for the minority group to correct for the amount of the systematic error, and to result in the same regression line. But if the minority group is over-predicted (as has often been the case where intercept differences have been observed), we would not want to use score adjustment to lower the minority group’s scores.

16.2.1.1.3 Different Intercepts and Slopes

Predictive bias in terms of different intercepts and slopes exists when there are differences in the intercept and slope of the regression line between minority and majority groups. In cases of different intercepts and slopes, there is both differential validity (because the regression lines have different slopes), as well as varying under- and over-estimation of groups’ performance at particular scores. Different intercepts and slopes predictive bias is depicted in Figure 16.7.

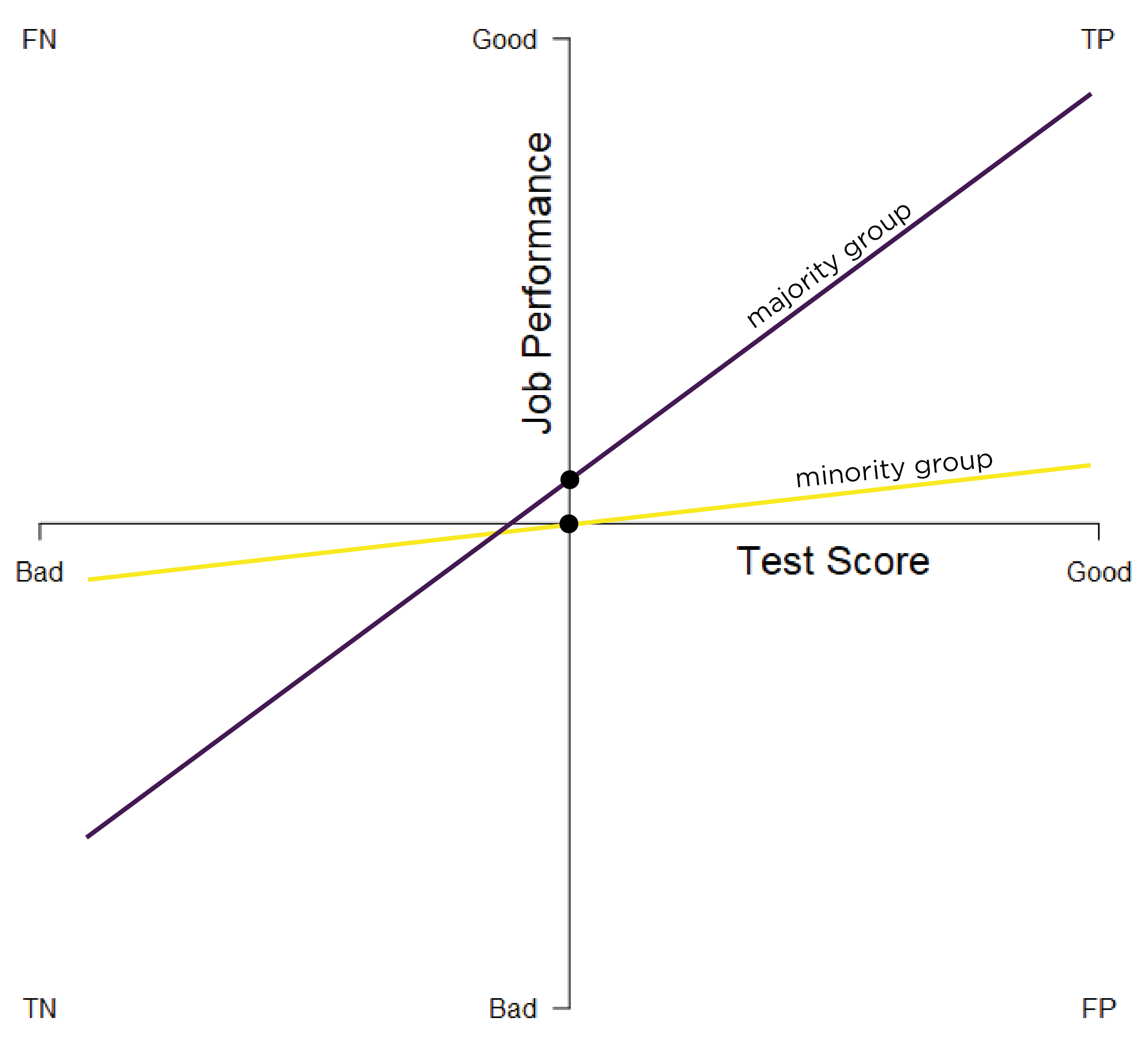
Figure 16.7: Test Bias: Different Intercepts and Slopes. TP = true positive; TN = true negative; FP = false positive; FN = false negative.

In instances of different intercepts and slopes predictive bias, a measure can simultaneously over-estimate and under-estimate a person’s ability at different test scores. For instance, a measure can under-estimate a person’s ability at higher test scores and can over-estimate a person’s ability at lower test scores.

Different intercepts and slopes across groups is possibly more realistic than just different intercepts or just different slopes. However, different intercepts and slopes predictive bias is more complicated to study, represent, and resolve. It is difficult to examine because of complexity, and it is not easy to fix. Currently, we have nothing to address different intercepts and slopes predictive bias. We would need to use a different measure or measures for each group.

16.2.2 Test Structure Bias

In addition to predictive bias, another type of test bias is test structure bias. Test structure bias involves differences in internal test characteristics across groups. Examining test structure bias is different from examining the total score, as is used when examining predictive bias. Test structure bias can be identified empirically or based on theory/judgment.

Empirically, test structure bias can be examined in multiple ways.

16.2.2.1 Empirical Approaches to Identification

16.2.2.1.1 Item \(\times\) Group tests (ANOVA)

Item \(\times\) Group tests in analysis of variance (ANOVA) examine whether the difference between groups on the overall score match comparisons among smaller items sets between groups. Item \(\times\) Group tests are used to rule out that items are operating in different ways in different groups. If the items operate in different ways in different groups, they do not have the same meaning across groups. For example, if we are going to use a measure for multiple groups, we would expect its items to operate similarly across groups. So, if women show higher scores on a depression measure compared to men, would also expect them to show similar elevations on each item (e.g., sleep loss).

16.2.2.1.2 Item Response Theory

Using item response theory, we can examine differential item functioning (DIF). Evidence of DIF, indicates that there are differences between group in terms of discrimination and/or difficulty/severity of items. Differences between groups in terms of the item characteristic curve (which combines the item’s discrimination and severity) would be evidence against construct validity invariance between the groups and would provide evidence of bias. DIF examines stretching and compression of different groups. As an example, consider the item “bites others” in relation to externalizing problems. The item would be expected to show a weaker discrimination and higher severity in adults compared to children. DIF is discussed in Section 16.9.

16.2.2.1.3 Confirmatory Factor Analysis

Confirmatory factor analysis allows tests of measurement invariance (also called factorial invariance). Measurement invariance examines whether the factor structure of the underlying latent variables in the test is consistent across groups. It also examines whether the manifestation of the construct differs between groups. Measurement invariance is discussed in Section 16.10.

Even if you find the same slope and intercepts across groups in a prediction model, the measure would still be assessing different constructs across groups if the measure has a different factor structure between the groups. A different factor structure across groups is depicted in Figure 16.8.

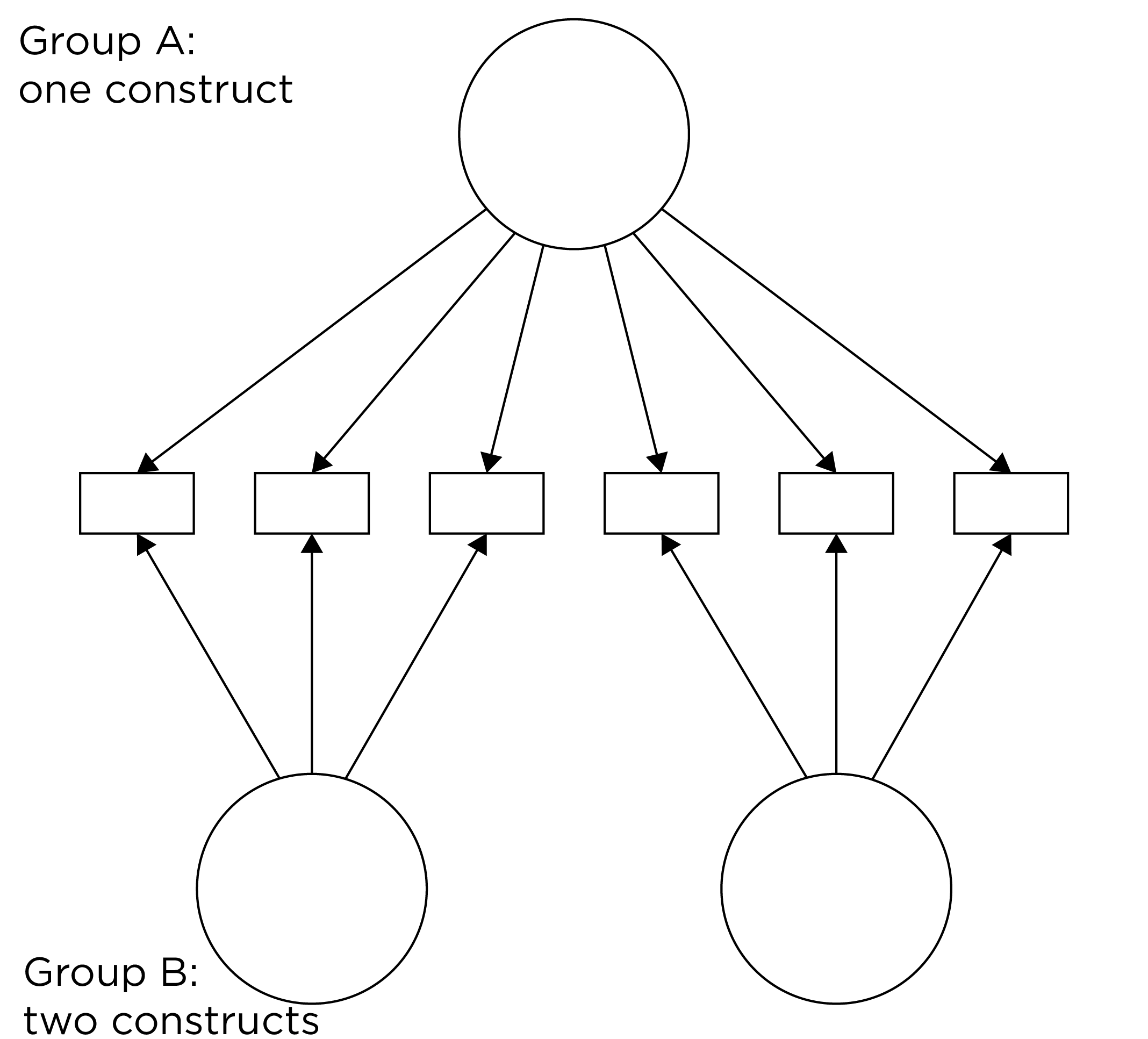
Figure 16.8: Different Factor Structure Across Groups.

An example of a different factor structure across groups is the differentiation of executive functions from two factors to three factors (inhibition, working memory, cognitive flexibility) across childhood (Lee et al., 2013).

There are different degrees of measurement invariance (for a review, see Putnick & Bornstein, 2016):

• Configural invariance: same number of factors in each group, and which indicators load on which factors are the same in each group (i.e., the same pattern of significant loadings in each group).
• Metric (“weak factorial”) invariance: items have the same factor loadings (discrimination) in each group.
• Scalar (“strong factorial”) invariance: items have the same intercepts (difficulty/severity) in each group.
• Residual (“strict factorial”) invariance: items have the same residual/unique variances in each group.

16.2.2.1.4 Structural Equation Modeling

Structural equation modeling is a confirmatory factor analysis (CFA) model that incorporates prediction. Structural equation modeling allows examining differences in the underlying structure with differences in prediction in the same model.

16.2.2.1.5 Signal Detection Theory

Signal detection theory is a dynamic measure of bias. It allows examining the overall bias in selection systems, including both accuracy and errors at various cutoffs (sensitivity, specificity, positive predictive value, and negative predictive value), as well as accuracy across all possible cutoffs (the area under the receiver operating characteristic curve). While there may be similar predictive validity between groups, the type of errors we are making across groups might differ. It is important to decide which types of error to emphasize depending on the fairness goals and examining sensitivity/specificity to adjust cutoffs.

16.2.2.1.6 Empirical Evidence of Test Structure Bias

It is not uncommon to find items that show differences across groups in severity (intercepts) and/or discrimination (factor loadings). However, cross-group differences in item functioning tend to be small and not consistent across studies, suggesting that some of the differences may reflect Type I errors that result from sampling error and multiple testing. That said, some instances of cross-group differences in item parameters could reflect test structure bias that is real and important to address.

16.2.2.2 Theoretical/Judgmental Approaches to Identification

16.2.2.2.1 Facial Validity Bias

Facial validity bias considers the extent to which an average person thinks that an item is biased—i.e., the item has differing validity between minority and majority groups. If so, the item should be reconsidered. Does an item disfavor certain groups? Is the language specific to a particular group? Is it offensive to some people? This type of judgment moves into the realm of whether or not an item should be used.

16.2.2.2.2 Content Validity Bias

Content validity bias is determined by judgments of construct experts who look for items that do not do an adequate job assessing the construct between groups. A construct may include some content facets in one group, but may include different content facets in another group, as depicted in Figure 16.9.

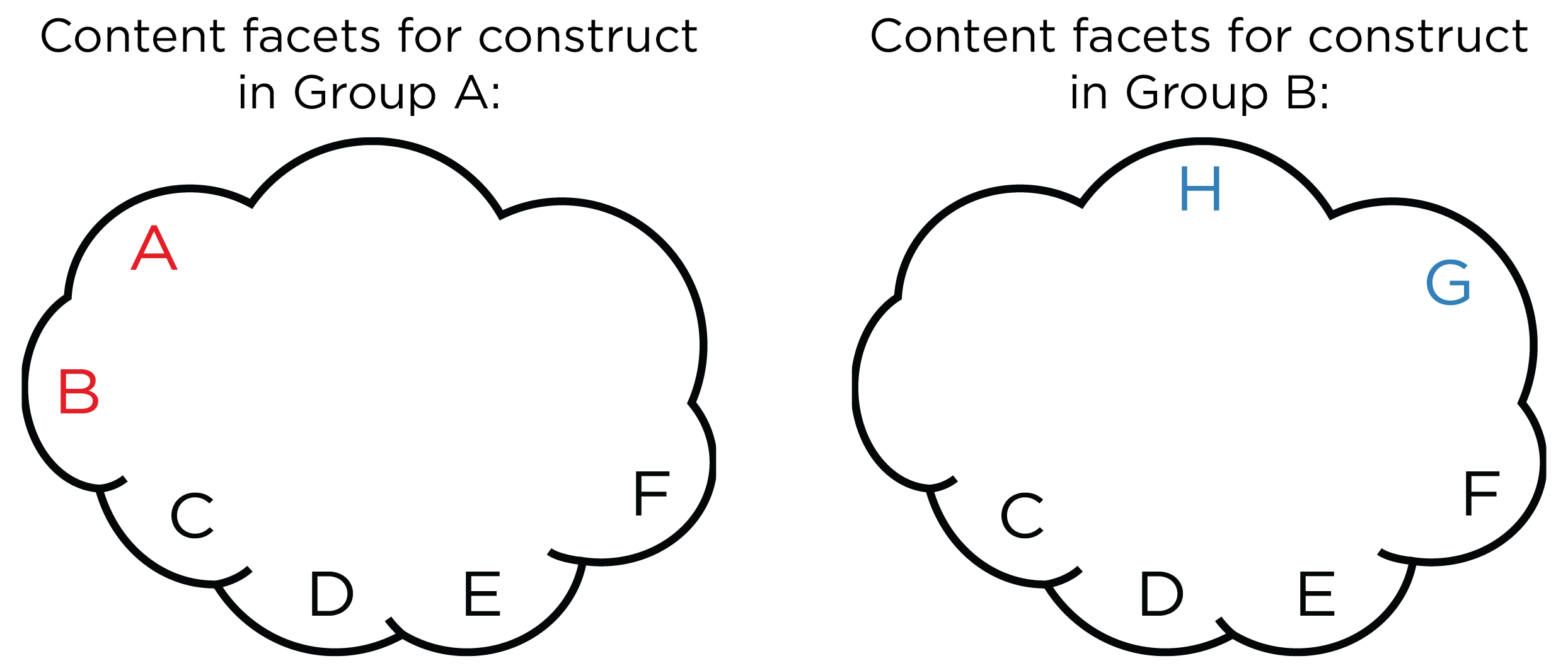
Figure 16.9: Different Content Facets in a Given Construct for Two Groups.

Examples include information questions and vocabulary questions on the Wechsler Adult Intelligence Scale. If an item is linguistically complicated, grammatically complex or convoluted, or a double negative, it may be less valid or predictive for rural populations and those with less education.

Also, stereotype threat may contribute to content validity bias. Stereotype threat occurs when people are or feel at risk of conforming themselves to stereotypes about their social group, thus leading them to show poorer performance in ways that are consistent with the stereotype. Stereotype threat may partially explain why some women may perform more poorly on some math items than some men.

Another example of content validity bias is when the same measure is used to assess a construct across ages even though the construct shows heterotypic continuity. Heterotypic continuity occurs when a construct changes in its behavioral manifestation with development (Petersen et al., 2020). That is, the same construct may look different at different points in development. An example of a construct that shows heterotypic continuity is externalizing problems. In early childhood, externalizing problems often manifest in overt forms, including physical aggression (e.g., biting) and temper tantrums. By contrast, in adolescence and adulthood, externalizing problems more often manifest in covert ways, including relational aggression and substance use. Content validity and facial validity bias judgments are often related, but not always.

16.3 Examples of Bias

As described in the overview in Section 16.1, there is not much empirical evidence of test bias (Brown et al., 1999; Hall et al., 1999; Jensen, 1980; Kuncel & Hezlett, 2010; Reynolds et al., 2021; Reynolds & Suzuki, 2012; Sackett et al., 2008; Sackett & Wilk, 1994). That said, some item-level bias is not uncommon. One instance of test bias is that, historically, women’s grades in math and engineering classes tended to be under-estimated by the Scholastic Aptitude Test [SAT; M. J. Clark & Grandy (1984)]. Fernández & Abe (2018) review the evidence on other instances of test and item bias. For instance, test bias can occur if a subgroup is less familiar with the language, the stimulus material, or the response procedures, or if they have different response styles. In addition to test bias, there are known patterns of bias in clinical judgment, as described in Section 25.3.11.

16.4 Test Fairness

There is interest in examining more than just the accuracy of measures. It is also important to examine the errors being made and differentiate the weight or value of different kinds of errors (and correct decisions). Consider an example of an unbiased test, as depicted in Figure 16.10, adapted from L. S. Gottfredson (1994). Although the example is of a White group and a Black group, we could substitute any two groups into the example (e.g., males versus females).

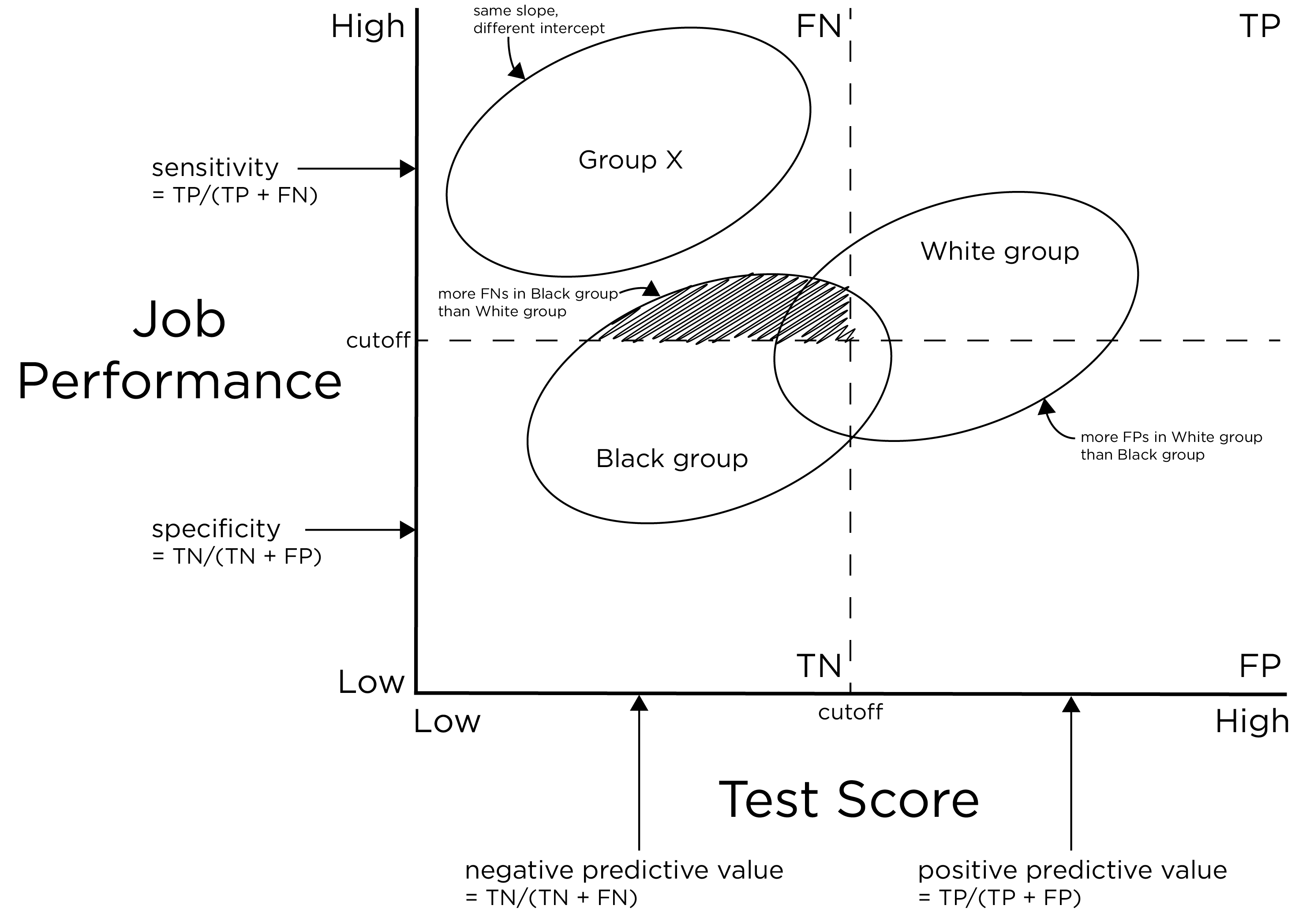
Figure 16.10: Potential Unfairness in Testing. The ovals represent the distributions of individuals’ performance both on a test and a job performance criterion. TP = true positive; TN = true negative; FP = false positive; FN = false negative. (Adapted from L. S. Gottfredson (1994), Figure 1, p. 958. Gottfredson, L. S. (1994). The science and politics of race-norming. American Psychologist, 49(11), 955–963. https://doi.org/10.1037/0003-066X.49.11.955)

The example is of an unbiased test between White and Black job applicants. There are no differences between the two groups in terms of slope. If we drew a regression line, the line would go through the centroid of both ovals. Thus, the measure is equally predictive in both groups even though that the Black group failed the test at a higher rate than the White group. Moreover, there is no difference between the groups in terms of intercept. Thus, the performance of one group is not over-estimated relative to the performance of the other group. To demonstrate what a different intercept would look like, Group X shows a different intercept. In sum, there is no predictive validity bias between the two groups. But just because the test predicts just as well in both groups does not mean that the selection procedures are fair.

Although the test is unbiased, there are differences in the quality of prediction: there are more false negatives in the Black group compared to the White group. This gives the White group an advantage and the Black group additional disadvantages. If the measure showed the same quality of prediction, we would say the test is fair. The point of the example is that just because a test is unbiased does not mean that the test is fair.

There are two kinds of errors: false negatives and false positives. Each error type has very different implications. False negatives would be when the test predicts that an applicant would perform poorly and we do not give them the job even though they would have performed well. False negatives have a negative effect on the applicant. And, in this example, there are more false negatives in the Black group. By contrast, false positives would be when we predict that an applicant would do well, and we give them the job but they perform poorly. False positives are a benefit to the applicant but have a negative effect on the employer. In this example, there are more false positives in the White group, which is an undeserved benefit based on the selection ratio; therefore, the White group benefits.

In sum, equal accuracy of prediction (i.e., equal total number of errors) does not necessarily mean the test is fair; we must examine the types of errors. Merely ensuring accuracy does not ensure fairness!

16.4.1 Adverse Impact

Adverse impact is defined as rejecting members of one group at a higher rate than another group. Adverse impact is different from test validity. According to federal guidelines, adverse impact is present if the selection rate of one group is less than four-fifths (80%) the selection rate of the group with the highest selection rate.

There is much more evidence of adverse impact than test bias. Indeed, disparate impact of tests on personnel selection across groups is the norm rather than the exception, even when using valid tests that are unbiased, which in part reflect group-related differences in job-related skills (L. S. Gottfredson, 1994). Examples of adverse impact include:

• physical ability tests, which produce substantial adverse impact against women (despite over-estimation of women’s performance),
• cognitive ability tests, which produce substantial impact against some ethnic minority groups, especially Black and Hispanic people (despite over-estimation of Black and Hispanic people’s performance), even though cognitive ability tests tend to be among the strongest predictors of job performance (Sackett et al., 2008; Schmidt & Hunter, 1981), and
• personality tests, which produce higher estimates of dominance among men than women; it is unclear whether this has predictive bias.

16.4.2 Bias Versus Fairness

Whether a measure is accurate or shows test bias is a scientific question. By contrast, whether a test is fair and thus should be used for a given purpose is not just a scientific question; it is also an ethical question. It involves the consideration of the potential consequences of testing in terms of social values and consequential validity.

16.4.3 Operationalizing Fairness

There are many perspectives to what should be considered when evaluating test fairness (American Educational Research Association et al., 2014; Camilli, 2013; Committee on the General Aptitude Test Battery et al., 1989; Dorans, 2017; Fletcher et al., 2021; Gipps & Stobart, 2009; Helms, 2006; Jonson & Geisinger, 2022; Melikyan et al., 2019; Sackett et al., 2008; Thorndike, 1971; Zieky, 2006, 2013). As described in Fletcher et al. (2021), there are three primary ways of operationalizing fairness:

1. Equal outcomes: the selection rate is the same across groups.
2. Equal opportunity: the sensitivity (true positive rate; 1 \(-\) false negative rate) is the same across groups.
3. Equal odds: the sensitivity is the same across groups and the specificity (true negative rate; 1 \(-\) false positive rate) is the same across groups.

For example, the job selection procedure shows equal outcomes if the proportion of men selected is equal to the proportion of women selected. The job selection procedure shows equal opportunity if, among those who show strong job performance, the proportion of classification errors (false negatives) is the same for men and women. Receiver operating characteristic (ROC) curves are depicted for two groups in Figure 16.11. A cutoff that represents equal opportunity is depicted with a horizontal line (i.e., the same sensitivity) in Figure 16.11. The job selection procedure shows equal odds if (a), among those who show strong job performance, the proportion of classification errors (false negatives) is the same for men and women, and (b), among those who show poor job performance, the proportion of classification errors (false positives) is the same for men and women. A cutoff that represents equal odds is depicted where the ROC curve for Group A intersects with the ROC curve from Group B in Figure 16.11. The equal odds approach to fairness is consistent with a National Academy of Sciences committee on fairness (Committee on the General Aptitude Test Battery et al., 1989; L. S. Gottfredson, 1994). Approaches to operationalizing fairness in the context of prediction models are described by Paulus & Kent (2020).

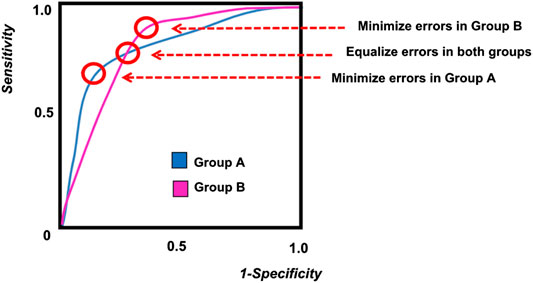
Figure 16.11: Receiver Operating Characteristic (ROC) Curves for Two Groups. (Figure reprinted from Fletcher et al. (2021), Figure 2, p. 3. Fletcher, R. R., Nakeshimana, A., & Olubeko, O. (2021). Addressing fairness, bias, and appropriate use of artificial intelligence and machine learning in global health. Frontiers in Artificial Intelligence, 3(116). https://doi.org/10.3389/frai.2020.561802)

It is not possible to meet all three types of fairness simultaneously (i.e., equal selection rates, sensitivity, and specificity across groups) unless the base rates are the same across groups or the selection is perfectly accurate (Fletcher et al., 2021). In the medical context, equal odds is the most common approach to fairness. However, using the cutoff associated with equal odds typically reduces overall classification accuracy. And, changing the cutoff for specific groups can lead to negative consequences. In the case that equal odds results in a classification accuracy that is too low, it may be worth considering using separate assessment procedures/tests for each group. In general, it is best to follow one of these approaches to fairness. It is difficult to get right, so try to minimize negative impact. Many fairness supporters argue for simpler rules. In the 1991 Civil Rights Act, score adjustments based on race, gender, and ethnicity (e.g., within-race norming or race-conscious score adjustments) were made illegal in personnel selection (L. S. Gottfredson, 1994).

Another perspective to fairness is that selection procedures should predict job performance and if they are correlated with any group membership (e.g., race, socioeconomic status, or gender), the test should not be used (Helms, 2006). That is, according to Helms, we should not use any test that assesses anything other than the construct of interest (job performance). Unfortunately, however, no measures like this exist. Every measure assesses multiple things, and factors such as poverty can have long-lasting impacts across many domains.

Another perspective to fairness is to make the selection procedures equal the number of successes within each group (Thorndike, 1971). According to this perspective, if you want to do selection, you should hire all people, then look at job performance. If among successful employees, 60% are White and 40% are Black, then set this selection rate for each group (i.e., hiring 80% White individuals and 20% Black individuals is not okay). According to this perspective, a selection system is only fair if the majority–minority differences on the selection device used are equal in magnitude to majority–minority differences in job performance. Selection criteria should be made based on prior distributions of success rates. However, you likely will not ever really know the true base rate in these situations. No one uses this approach because you would have a period where you have to accept everyone to find the percent that works. Also, this would only work in a narrow window of time because the selection pool changes over time.

There are lots of groups and subgroups. Ensuring fairness is very complex, and there is no way to accomplish the goal of being equally fair to all people. Therefore, do the best you can and try to minimize negative impact.

16.5 Correcting For Bias

16.5.1 What to Do When Detecting Bias

When examining item bias (using differential item functioning/DIF or measurement non-invariance) with many items (or measures) across many groups, there can be many tests, which will make it likely that DIF/non-invariance will be detected, especially with a large sample. Some detected DIF may be artificial or trivial, but other DIF may be real and important to address. It is important to consider how you will proceed when detecting DIF/non-invariance. Considerations of effect size and theory can be important for evaluating the DIF/non-invariance and whether it is negligible or important to address.

When detecting bias, there are several steps to take. First, consider what the bias indicates. Does the bias present adverse impact for a minority group? For what reasons might the bias exist? Second, examine the effect size of the bias. If the effects are small, if the bias does not present adverse impact for a minority group, and if there is no compelling theoretical reason for the bias, the bias might not be sufficient to scrap the instrument for the population. Some detected bias may be artificial, but other bias may be real. Gender and cultural differences have shown a number of statistically significant effects for a number of different assessment purposes, but many of the observed effects are quite small and likely trivial, and they do not present compelling reasons to change the assessment (Youngstrom & Van Meter, 2016).

However, if you find bias, correct for it! There are a number of score adjustment and non-score adjustment approaches to correct for bias, as described in Sections 16.5.2 and 16.5.3. If the bias occurs at the item level (e.g., test structure bias), it is generally recommended to remove or resolve items that show non-negligible bias. There are three primary options: (1) drop the item for both groups, (2) drop the item for one group but keep it for the other group, or (3) freely estimate the parameters for the item across groups. Addressing items that show larger bias can also reduce artificial bias in other items (Hagquist & Andrich, 2017). Thus, researchers are encouraged to handle item bias sequentially from high to low in magnitude. If the bias occurs at the test score level (e.g., predictive bias), score adjustments may be considered.

If you do not correct for bias, consider the impact of the test, procedure, and selection procedure when interpreting scores. Interpret scores with caution and provide necessary caveats in resulting papers or reports regarding the interpretations in question. In sum, it is important to examine the possibility of bias—it is important to consider how much “erroneous junk” you are introducing into your research.

16.5.2 Score Adjustment to Correct for Bias

Score adjustment involves adjusting scores for a particular group or groups.

16.5.2.1 Why Adjust Scores?

There may be several reasons to adjust scores for various groups in a given situation. First, there may be social goals to adjust scores. For example, we may want our selection device to yield personnel that better represent the nation or region, including diversity of genders, races, majors, social classes, etc. Score adjustments are typically discussed with respect to racial minority differences due to historical and systemic inequities. Our society aims to provide equal opportunity, including the opportunity to gain a fair share (i.e., proportional representation) of jobs. A diversity of perspectives in a job is a strength; a diversity of perspectives can lead to greater creativity and improved problem-solving. A second potential reason that we may want to apply score adjustment is to correct for bias. A third potential reason that we may want to apply score adjustment is to improve the fairness of a test.

16.5.2.2 Types of Score Adjustment

There are a number of potential techniques that have been used in attempts to correct for bias, i.e., to reduce negative impact of the test on an under-represented group. What is considered an under-represented group may depend on the context. For instance, men are under-represented compared to women as nurses, preschool teachers, and college students. However, men may not face the same systemic challenges compared to women, so even though men may show under-representation in some domains, it is arguable whether scores should be adjusted to increase their representation. Techniques for score adjustment include:

• Bonus points
• Within-group norming
• Separate cutoffs
• Top-down selection from different lists
• Banding
• Banding with bonus points
• Sliding band
• Separate tests
• Item elimination based on group differences

16.5.2.2.1 Bonus Points

Providing bonus points involves adding a constant number of points to the scores of all individuals who are members of a particular group with the goal of eliminating or reducing group differences. Bonus points is used to correct for predictive bias differences in intercepts between groups. An example of bonus points is military veterans in placement for civil service jobs—points are added to the initial score for all veterans (e.g., add 5 points to test scores of all veterans). An example of using bonus points as a score adjustment is depicted in Figure 16.12.

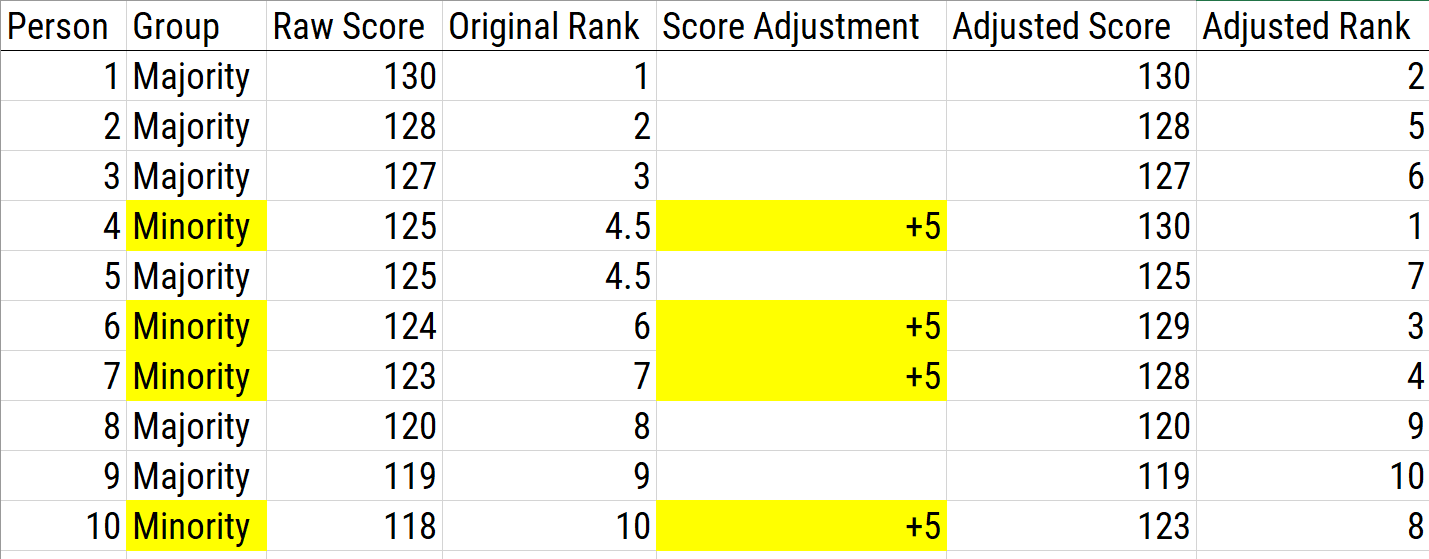
Figure 16.12: Using Bonus Points as a Scoring Adjustment.

There are several pros of bonus points. If the distribution of each group is the same, this will effectively reduce group differences. Moreover, it is a simple way of impacting test selection and procedure without changing the test, which is therefore a great advantage. There are several cons of bonus points. If there are differences in group standard deviations, adding bonus points may not actually correct for bias. The use of bonus points also obscures what is actually being done to scores, so other methods like using separate cutoffs may be more explicit. In addition, the simplicity of bonus points is also a great disadvantage because it is easily understood and often not viewed as “fair” because some people are getting extra points that others do not.

16.5.2.2.2 Within-Group Norming

A norm is the standard of performance that a person’s performance can be compared to. Within-group norming treats the person’s group in the sample as the norm. Within-group norming converts an individual’s score to standardized scores (e.g., T scores) or percentiles within one’s own group. Then, the people are selected based on the highest standard scores across groups. Withing-group norming is used to correct for predictive bias differences in slopes between groups. An example of using within-group norming as a score adjustment is depicted in Figure 16.13.

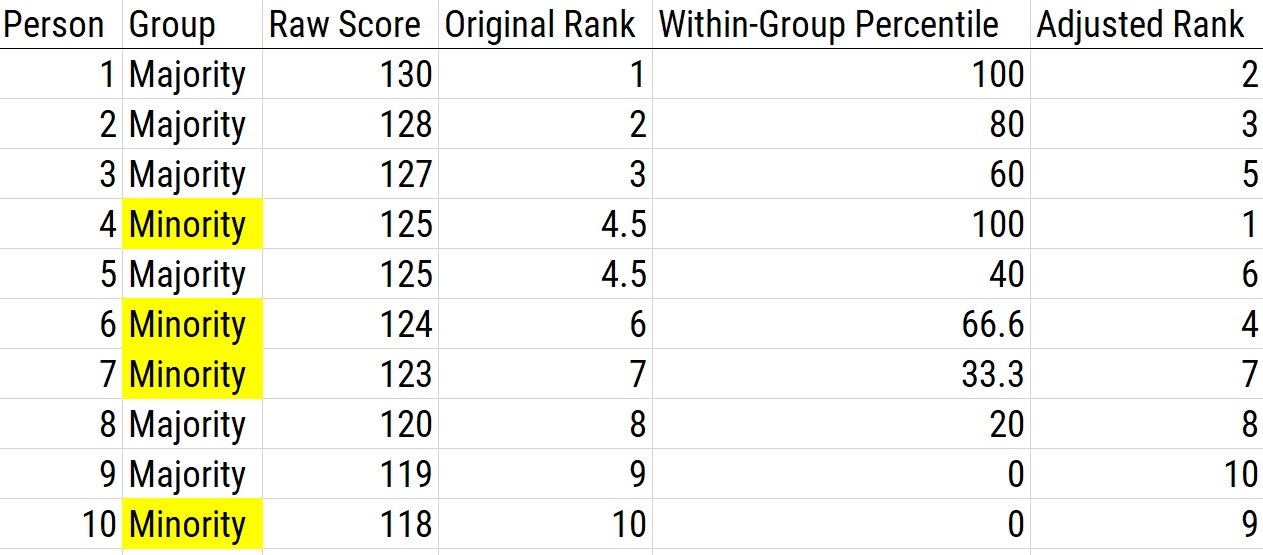
Figure 16.13: Using Within-Group Norming as a Scoring Adjustment.

There are several pros of within-group norming. First, it accounts for differences in group standard deviations and means, so it does not have the same problem as bonus points and is generally more effective at eliminating adverse impact compared to bonus points. Second, some general (non-group-specific) norms are clearly irrelevant for characterizing a person’s functioning. Group-specific norms aim to describe a person’s performance relative to people with a similar background, thus potentially reducing cultural bias. Third, group-specific norms may better reflect cultural, educational, socioeconomic, and other factors that may influence a person’s score (Burlew et al., 2019). Fourth, group-specific norms may increase specificity, and reduce over-pathologizing by preventing giving a diagnosis to people who might not show a condition (Manly & Echemendia, 2007).

There are several cons of within-group norming. First, group differences could be maintained if one decides to norm based on a reference sample or, when scores are skewed, a local sample, especially when using standardized scores. However, percentile scores will consistently eliminate adverse impact. Second, using group-specific norms may obscure background variables that explain underlying reasons for group-related differences in test performance (Manly, 2005; Manly & Echemendia, 2007). Third, group-specific norms do not address the problem if the measure shows test bias (Burlew et al., 2019). Fourth, group-specific norms may reduce sensitivity to detect conditions (Manly & Echemendia, 2007). For instance, they may prevent people from getting treatment who would benefit. It is worth noting that within-group norming on the basis of sex, gender, and ethnicity is illegal for the basis of personnel selection according to the 1991 Civil Rights Act.

As an example of within-group norming, the National Football League used to use race-norming for identification of concussions. The effect of race-norming, however, was that it lowered Black players’ concussion risk scores, which prevented many Black players from being identified as having sustained a concussion and from receiving needed treatment. Race-norming compared the Black football players cognitive test scores to group-specific norms: the cognitive test scores of Black people in the general population (not to common norms). Using Black-specific norms assumed that Black football players showed lower cognitive ability than other groups, so a low cognitive ability score for a Black player was less likely to be flagged as concerning. Thus, the race-specific norms led to lower identified rates of concussions among Black football players compared to White football players. Due to the adverse impact, Black players sued the National Football League, and the league stopped the controversial practice of race-norming for identification of concussion (https://www.washingtonpost.com/sports/2021/06/03/nfl-concussion-settlement-race-norming/; archived at https://perma.cc/KN3L-5Z7R).

A common question is whether to use group-specific norms or common norms. Group-specific norms are a controversial practice, and the answer depends. If you are interested in a person’s absolute functioning (e.g., for determining whether someone is concussed or whether they are suitable to drive), recommendations are to use common norms, not group-specific norms (Barrash et al., 2010; Silverberg & Millis, 2009). If, by contrast, you are interested in a person’s relative functioning compared to a specific group, within-group norming could make sense if there is an appropriate reference group. The question about which norms to use are complex, and psychologists should evaluate the cost and benefit of each norm, and use the norm with the greatest benefit and the least cost for the client (Manly & Echemendia, 2007).

16.5.2.2.3 Separate Cutoffs

Using separate cutoffs involves using a separate cutoff score per group and selecting the top number from each group. That is, using separate cutoffs involves using different criteria for each group. Using separate cutoffs functions the same as adding bonus points, but it has greater transparency—i.e., you are lowering the standard for one group compared to another group. An example of using separate cutoffs as a score adjustment is depicted in Figure 16.14.

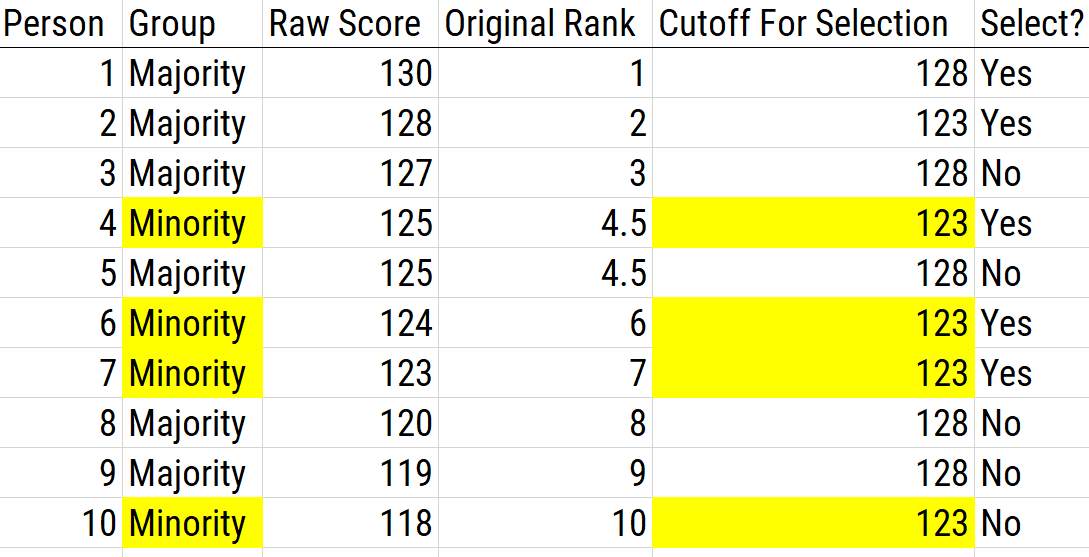
Figure 16.14: Using Separate Cutoffs as a Scoring Adjustment. In this example, the cutoff for the majority group is 128; the cutoff for the minority group is 123.

16.5.2.2.4 Top-Down Selection from Different Lists

Top-down selection from different lists involves taking the best from two different lists according to a preset rule as to how many to select from each group. Top-down selection from different lists functions the same as within-group norming. An example of using top-down selection from different lists as a score adjustment is depicted in Figure 16.15.

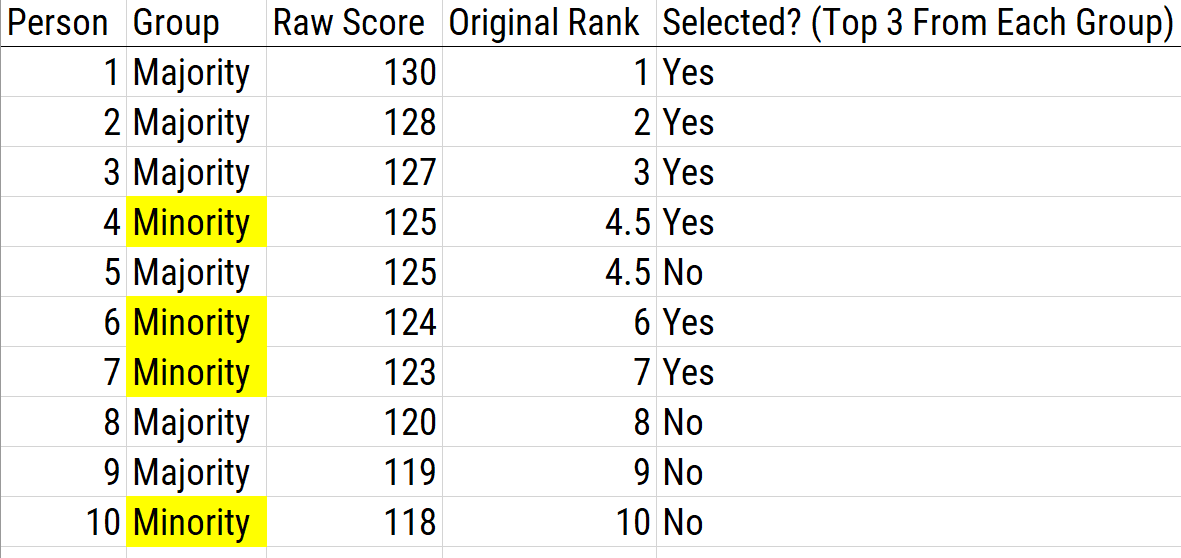
Figure 16.15: Using Top-Down Selection From Different Lists as a Scoring Adjustment. In this example, the top three candidates are selected from each group.

16.5.2.2.5 Banding

Banding uses a tier system that is based on the assumption that individuals within a specific score range are regarded as having equivalent scores. So that we do not over-estimate small score differences, scores within the same band are seen as equivalent—and the order of selection within the band can be modified depending on selection goals. The standard error of measurement (SEM) is used to estimate the precision (reliability) of the test scores, and it is used as the width of the band.

Consider an example: if a person received a score with confidence interval of 18–22, then scores between 18 to 22 are not necessarily different due to random fluctuation (measurement error). Therefore, scores in that range are considered the same, and we take a band of scores. However, banding by itself may not result in increased selection of lower scoring groups. The band provides a subsample of applicants so that we can use other criteria (other than the test) to select a candidate. Giving “minority preference” involves selecting members of minority group in a given band before selecting members of the majority group. An example of using banding as a score adjustment is depicted in Figure 16.16.

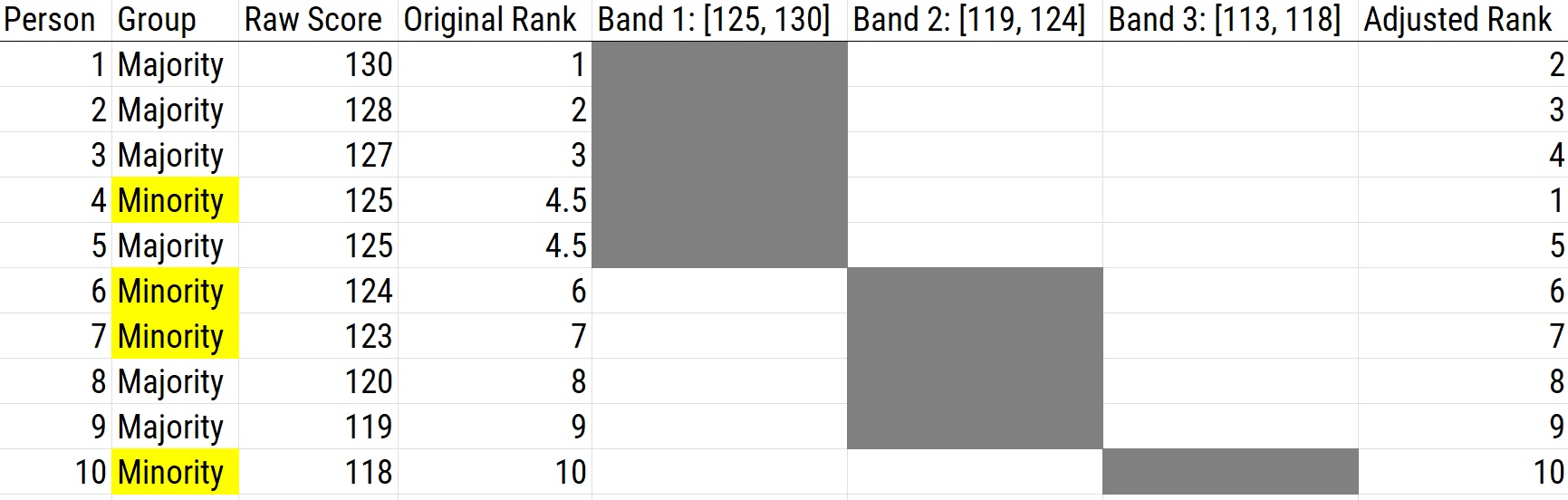
Figure 16.16: Using Banding as a Scoring Adjustment.

The problem with banding is that bands are set by the standard error of measurement: you can select the first group from the first band, but then whom do you select after the first band? There is no rationale where to “stop” the band because there are indistinguishable scores on the edges of each band to the next band. That is, 17 is indistinguishable from 18 (in terms of its confidence interval), 16 is indistinguishable from 17, and so on. Therefore, banding works okay for the top scores, but if you are going to hire a lot of candidates, it is a problem. A solution to this problem with banding is to use a sliding band, as described later.

16.5.2.2.6 Banding with Bonus Points

Banding is often used with bonus points to reduce the negative impact for minority groups. An example of using banding with bonus points as a score adjustment is depicted in Figure 16.17.

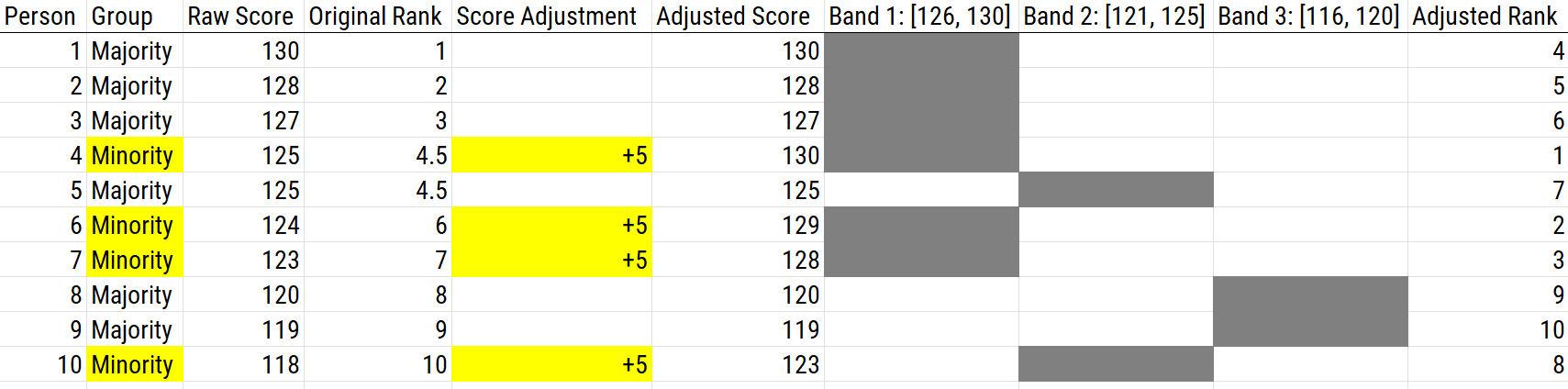
Figure 16.17: Using Banding With Bonus Points as a Scoring Adjustment.

16.5.2.2.7 Sliding Band

Using a sliding band is a solution to the problem of which bands to use when using banding. Using a sliding band can help increase the number of minorities selected. Using the top band, you select all members of a minority group in the top band, then select members of the majority group with the top score of the band, then slide the band down (based on SEM), and repeat. You work your way down with bands though groups that are indistinguishable based on SEM, until getting a cell needed to select a relevant candidate.

For instance, if the top score is 22 and the SEM is 4 points, the first band would be: [18, 22]. Here is how you would proceed:

1. Select the minority group members who have a score between 18 to 22.
2. Select the majority group members who have a score of 22.
3. Slide the band down based on the SEM to the next highest score: [17, 21].
4. Select the minority group members who have a score between 17 to 21.
5. Select the majority group members who have a score of 21.
6. Slide the band down based on the SEM to the next highest score: [16, 20].
7. …
8. And so on

An example of using a sliding band as a score adjustment is depicted in Figure 16.18.

Figure 16.18: Using a Sliding Band as a Scoring Adjustment.

In sum, using a sliding band, scores that are not significantly lower than the highest remaining score should not be treated as different. Using a sliding band has the same effects on decisions as bonus points that are the width of the band. For example, if the SEM is 3, it has the same decisions as bonus points of 3; therefore, any scores within 3 of the highest score are now considered equal.

A sliding band is popular because of its scientific and statistical rationale. Also, it is more confusing and, therefore, preferred by some because it may be less likely to be sued. However, a sliding band may not always eliminate adverse impact. A sliding band has never been overturned in court (or at least, not yet).

16.5.2.2.8 Separate Tests

Using separate tests for each group is another option to reduce bias. For instance, you might use one test for the majority group and a different test for the minority group, making sure that each test is valid for the relevant group. Using separate tests is an extreme version of top-down selection and within-group norming. Using separate tests would be an option if a measure shows different slopes predictive bias.

One way of developing separate tests is to use empirical keying by group: different items for each group are selected based on each item’s association with the criterion in each group. Empirical keying is an example of dustbowl empiricism (i.e., relying on empiricism rather than theory). However, theory can also inform the item selection.

16.5.2.2.9 Item Elimination based on Group Differences

Items that show large group differences in scores can be eliminated from the test. If you remove enough items showing differences between groups, you can get similar scores between groups and can get equal group selection. A problem of item elimination based on group differences is that if you get rid of predictive items, then two goals, equal selection and predictive power, are not met. If you use this method, you often have to be willing for the measure to show decreases in predictive power.

16.5.2.3 Use of Score Adjustment

Score adjustment can be used in a number of different domains, including tests of aptitude and intelligence. Score adjustment also comes up in other areas. For example, the number of drinks it takes to be considered binge drinking differs between men (five) and women (four). Although the list of score adjustment options is long, they all really reduce to two ways:

1. Bonus points
2. Within-group norming

Bonus points and within-group norming are the techniques that are most often used in the real world. These techniques differ in their degree of obscurity—i.e., confusion that is caused not for scientific reasons, but for social, political, and dissemination and implementation reasons. Often procedures that are hard to understand are preferred because it is hard to argue against, critique, or game the system. Basically, you have two options for score adjustment. One option is to adjust scores by raising scores in one group or lowering the criterion in one group. The second primary option is to renorm or change the scores. In sum, you can change the scores, or you can change the decisions you make based on the scores.

16.5.3 Other Ways to Correct for Bias

Because score adjustment is controversial, it is also important to consider other potential ways to correct for bias that do not involve score adjustment. Strategies other than score adjustment to correct for bias are described by Sackett et al. (2001).

16.5.3.1 Use Multiple Predictors

In general, high-stakes decisions should not be made based on the results from one test. So, for instance, do not make hiring decisions based just on aptitude assessments. For example, college admissions decisions are not made just based on SAT scores, but also one’s grades, personal statement, extracurricular activities, letters of recommendation, etc. Using multiple predictors works best when the predictors are not correlated with the assessment that has adverse impact, which is difficult to achieve.

There are larger majority–minority subgroup differences in verbal and cognitive ability tests than in noncognitive skills (e.g., motivation, personality, and interpersonal skills). So, it is important to include assessment of relevant noncognitive skills. Include as many relevant aspects of the construct as possible for content validity. For a job, consider as many factors as possible that are relevant for success, e.g., cognitive and noncognitive abilities.

16.5.3.2 Change the Criterion

Another option is to change the criterion so that the predictive validity of tests is less skewed. It may be that the selection instrument is not biased but the way in which we are thinking about selection procedures is biased. For example, for judging the quality of universities, there are many different criteria we could use. It could be valuable to examine the various criteria, and you might find what is driving adverse effects.

16.5.3.3 Remove Biased Items

Using item response theory or confirmatory factor analysis, you can identify items that function differently across groups (i.e., differential item functioning/DIF or measurement non-invariance). For instance, you can identify items that show different discrimination/factor loadings or difficulty/intercepts by group. You do not just want to remove items that show mean-level differences in scores (or different rates of endorsement) for one group than another, because there may be true group differences in their level on particular items. If an item is clearly invalid in one group but valid in another group, another option is to keep the item in one group, and to remove it in another group.

Be careful when removing items because removing items can lead to poorer content validity—i.e., items may no longer be a representative set of the content of the construct. Removing items also reduces a measure’s reliability and ability to detect individual differences (Hagquist, 2019; Hagquist & Andrich, 2017). DIF effects tend to be small and inconsistent; removing items showing DIF may not have a big impact.

16.5.3.4 Resolve Biased Items

Another option, for items identified that show differential item functioning using IRT or measurement non-invariance using CFA, is to resolve instead of remove items. Resolving items involves allowing an item to have a different discrimination/factor loading and/or difficulty/intercept parameter for each group. Allowing item parameters to differ across groups has a very small effect on reliability and person separation, so it can be preferable to removing items (Hagquist, 2019; Hagquist & Andrich, 2017).

16.5.3.5 Use Alternative Modes of Testing

Another option is to use alternative modes of testing. For example, you could use audio or video to present test items, rather than requiring a person to read the items, or write answers. Typical testing and computerized exams are oriented toward the upper-middle class, which is therefore a procedure problem! McClelland’s (1973) argument is that we need more real-life testing. Real-life testing could help address stereotype threats and the effects of learning disabilities. However, testing in different modalities could change the construct(s) being assessed.

16.5.3.6 Use Work Records

Using work records is based on McClelland’s (1973) argument to use more realistic and authentic assessments of job-relevant abilities. Evidence on the value of work records for personnel selection is mixed. In some cases, use of work records can actually increase adverse impact on under-represented groups because the primary group typically already has an idea of how to get into the relevant job or is already in the relevant job; therefore, they have a leg up. It would be acceptable to use work records if you trained people first and then tested, but no one spends the time to do this.

16.5.3.7 Increase Time Limit

Another option is to allot people more testing time, as long as doing so does not change the construct. Time limits often lead to greater measurement error because scores conflate pace and quality of work. Increasing time limits requires convincing stakeholders that job performance is typically not “how fast you do things” but “how well you do them”—i.e., that time does not correlate with outcome of interest. The utility of increasing time limits depends on the domain. In some domains, efficiency is crucial (e.g., medicine, pilot). Increasing time limits is not that effective in reducing group differences, and it may actually increase group differences.

16.5.3.8 Use Motivation Sets

Using motivation sets involves finding ways to increase testing motivation for minority groups. It is probably an error to think that a test assesses just aptitude; therefore, we should also consider an individual’s motivation to test. Thus, part of the score has to do with ability and some of the score has to do with motivation. You should try to maximize each examinee’s motivation, so that the person’s score on the measure better captures their true ability score. Motivation sets could include, for example, using more realistic test stimuli that are clearly applicable to the school or job requirements (i.e., that have face validity) to motivate all test takers.

16.5.3.9 Use Instructional Sets

Using instructional sets involves coaching and training. For instance, you could inform examinees about the test content, provide study materials, and recommend test-taking strategies. This could narrow the gap between groups because there is an implicit assumption that the primary group already has “light” training. Using instructional sets aims to reduce error variance due to test anxiety, unfamiliar test format, and poor test-taking skills.

Giving minority groups better access to test preparation is based on the assumption that group differences emerge because of different access to test preparation materials. This could theoretically help to systematically reduce test score differences across groups. Standardized tests like the SAT/GRE/LSAT/GMAT/MCAT, etc. embrace coaching/training. For instance, the organization ETS gives training materials for free. After training, scores on standardized tests show some but minimal improvement. In general, training yields some improvement on quantitative subscales but minimal change on verbal subscales. However, the improvements tend to apply across groups, and they do not seem to lessen group differences in scores.

16.6 Getting Started

16.6.1 Load Libraries

Code

library("petersenlab") #to install: install.packages("remotes"); remotes::install_github("DevPsyLab/petersenlab")
library("lavaan")
library("semTools")
library("semPlot")
library("mirt")
library("dmacs") #to install: install.packages("remotes"); remotes::install_github("ddueber/dmacs")
library("strucchange")
library("MOTE")
library("tidyverse")
library("here")
library("tinytex")

16.6.2 Prepare Data

16.6.2.1 Load Data

cnlsy is a subset of a data set from the Children of the National Longitudinal Survey of Youth Survey (CNLSY). The CNLSY is a publicly available longitudinal data set provided by the Bureau of Labor Statistics (https://perma.cc/EH38-HDRN). The CNLSY data file for these examples is located on the book’s page of the Open Science Framework (https://osf.io/3pwza).

Code

cnlsy <- read_csv(here("Data", "cnlsy.csv"))

16.6.2.2 Simulate Data

For reproducibility, I set the seed below. Using the same seed will yield the same answer every time. There is nothing special about this particular seed.

Code

sampleSize <- 4000

set.seed(52242)

mydataBias <- data.frame(
  ID = 1:sampleSize,
  group = factor(c("male","female"),
                 levels = c("male","female")),
  unbiasedPredictor1 = NA,
  unbiasedPredictor2 = NA,
  unbiasedPredictor3 = NA,
  unbiasedCriterion1 = NA,
  unbiasedCriterion2 = NA,
  unbiasedCriterion3 = NA,
  predictor = rnorm(sampleSize, mean = 100, sd = 15),
  criterion1 = NA,
  criterion2 = NA,
  criterion3 = NA,
  criterion4 = NA,
  criterion5 = NA)

mydataBias$unbiasedPredictor1 <- rnorm(sampleSize, mean = 100, sd = 15)
mydataBias$unbiasedPredictor2[which(mydataBias$group == "male")] <- 
  rnorm(length(which(mydataBias$group == "male")), mean = 70, sd = 15)
mydataBias$unbiasedPredictor2[which(mydataBias$group == "female")] <- 
  rnorm(length(which(mydataBias$group == "female")), mean = 130, sd = 15)
mydataBias$unbiasedPredictor3[which(mydataBias$group == "male")] <- 
  rnorm(length(which(mydataBias$group == "male")), mean = 130, sd = 15)
mydataBias$unbiasedPredictor3[which(mydataBias$group == "female")] <- 
  rnorm(length(which(mydataBias$group == "female")), mean = 70, sd = 15)

mydataBias$unbiasedCriterion1 <- 1 * mydataBias$unbiasedPredictor1 + 
  rnorm(sampleSize, mean = 0, sd = 15)
mydataBias$unbiasedCriterion2 <- 1 * mydataBias$unbiasedPredictor2 + 
  rnorm(sampleSize, mean = 0, sd = 15)
mydataBias$unbiasedCriterion3 <- 1 * mydataBias$unbiasedPredictor3 + 
  rnorm(sampleSize, mean = 0, sd = 15)

mydataBias$criterion1[which(mydataBias$group == "male")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "male")] + 
  rnorm(length(which(mydataBias$group == "male")), mean = 0, sd = 5)
mydataBias$criterion1[which(mydataBias$group == "female")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "female")] + 
  rnorm(length(which(mydataBias$group == "female")), mean = 0, sd = 5)
mydataBias$criterion2[which(mydataBias$group == "male")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "male")] + 
  rnorm(length(which(mydataBias$group == "male")), mean = 10, sd = 5)
mydataBias$criterion2[which(mydataBias$group == "female")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "female")] + 
  rnorm(length(which(mydataBias$group == "female")), mean = 0, sd = 5)
mydataBias$criterion3[which(mydataBias$group == "male")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "male")] + 
  rnorm(length(which(mydataBias$group == "male")), mean = 0, sd = 5)
mydataBias$criterion3[which(mydataBias$group == "female")] <- 
  .3 * mydataBias$predictor[which(mydataBias$group == "female")] + 
  rnorm(length(which(mydataBias$group == "female")), mean = 0, sd = 5)
mydataBias$criterion4[which(mydataBias$group == "male")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "male")] + 
  rnorm(length(which(mydataBias$group == "male")), mean = 0, sd = 5)
mydataBias$criterion4[which(mydataBias$group == "female")] <- 
  .3 * mydataBias$predictor[which(mydataBias$group == "female")] + 
  rnorm(length(which(mydataBias$group == "female")), mean = 30, sd = 5)
mydataBias$criterion5[which(mydataBias$group == "male")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "male")] + 
  rnorm(length(which(mydataBias$group == "male")), mean = 0, sd = 30)
mydataBias$criterion5[which(mydataBias$group == "female")] <- 
  .7 * mydataBias$predictor[which(mydataBias$group == "female")] + 
  rnorm(length(which(mydataBias$group == "female")), mean = 0, sd = 5)

16.6.2.3 Add Missing Data

Adding missing data to dataframes helps make examples more realistic to real-life data and helps you get in the habit of programming to account for missing data.

HolzingerSwineford1939 is a data set from the lavaan package (Rosseel et al., 2022) that contains mental ability test scores (x1–x9) for seventh- and eighth-grade children.

Code

varNames <- names(mydataBias)
dimensionsDf <- dim(mydataBias[,-c(1,2)])
unlistedDf <- unlist(mydataBias[,-c(1,2)])
unlistedDf[sample(
  1:length(unlistedDf),
  size = .01 * length(unlistedDf))] <- NA
mydataBias <- cbind(
  mydataBias[,c("ID","group")],
  as.data.frame(
    matrix(
      unlistedDf,
      ncol = dimensionsDf[2])))
names(mydataBias) <- varNames

data("HolzingerSwineford1939")
varNames <- names(HolzingerSwineford1939)
dimensionsDf <- dim(HolzingerSwineford1939[,paste("x", 1:9, sep = "")])
unlistedDf <- unlist(HolzingerSwineford1939[,paste("x", 1:9, sep = "")])
unlistedDf[sample(
  1:length(unlistedDf),
  size = .01 * length(unlistedDf))] <- NA
HolzingerSwineford1939 <- cbind(
  HolzingerSwineford1939[,1:6],
  as.data.frame(matrix(
    unlistedDf,
    ncol = dimensionsDf[2])))
names(HolzingerSwineford1939) <- varNames

16.7 Examples of Unbiased Tests (in Terms of Predictive Bias)

16.7.1 Unbiased test where males and females have equal means on predictor and criterion

Figure 16.19 depicts an example of an unbiased test where males and females have equal means on the predictor and criterion. The test is unbiased because there are no significant differences in the regression lines (of predictor predicting criterion) between males and females.

Code

summary(lm(
  unbiasedCriterion1 ~ unbiasedPredictor1 + group + unbiasedPredictor1:group,
  data = mydataBias))

Call:
lm(formula = unbiasedCriterion1 ~ unbiasedPredictor1 + group + 
    unbiasedPredictor1:group, data = mydataBias)

Residuals:
    Min      1Q  Median      3Q     Max 
-54.623 -10.050  -0.025  10.373  66.811 

Coefficients:
                                Estimate Std. Error t value Pr(>|t|)    
(Intercept)                     0.930697   2.295058   0.406    0.685    
unbiasedPredictor1              0.996976   0.022624  44.066   <2e-16 ***
groupfemale                    -1.165200   3.250481  -0.358    0.720    
unbiasedPredictor1:groupfemale -0.004397   0.032115  -0.137    0.891    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 15.13 on 3913 degrees of freedom
  (83 observations deleted due to missingness)
Multiple R-squared:  0.4963,    Adjusted R-squared:  0.496 
F-statistic:  1285 on 3 and 3913 DF,  p-value: < 2.2e-16

Code

plot(
  unbiasedCriterion1 ~ unbiasedPredictor1,
  data = mydataBias,
  xlim = c(
    0, 
    max(c(
      mydataBias$unbiasedCriterion1,
      mydataBias$unbiasedPredictor1),
      na.rm = TRUE)),
  ylim = c(
    0, 
    max(c(
      mydataBias$criterion1,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$unbiasedPredictor1[which(mydataBias$group == "male")],
  mydataBias$unbiasedCriterion1[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(mydataBias$unbiasedPredictor1[which(mydataBias$group == "female")],
       mydataBias$unbiasedCriterion1[which(mydataBias$group == "female")],
       pch = 1,
       col = "red")
abline(lm(
  unbiasedCriterion1 ~ unbiasedPredictor1,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  unbiasedCriterion1 ~ unbiasedPredictor1,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))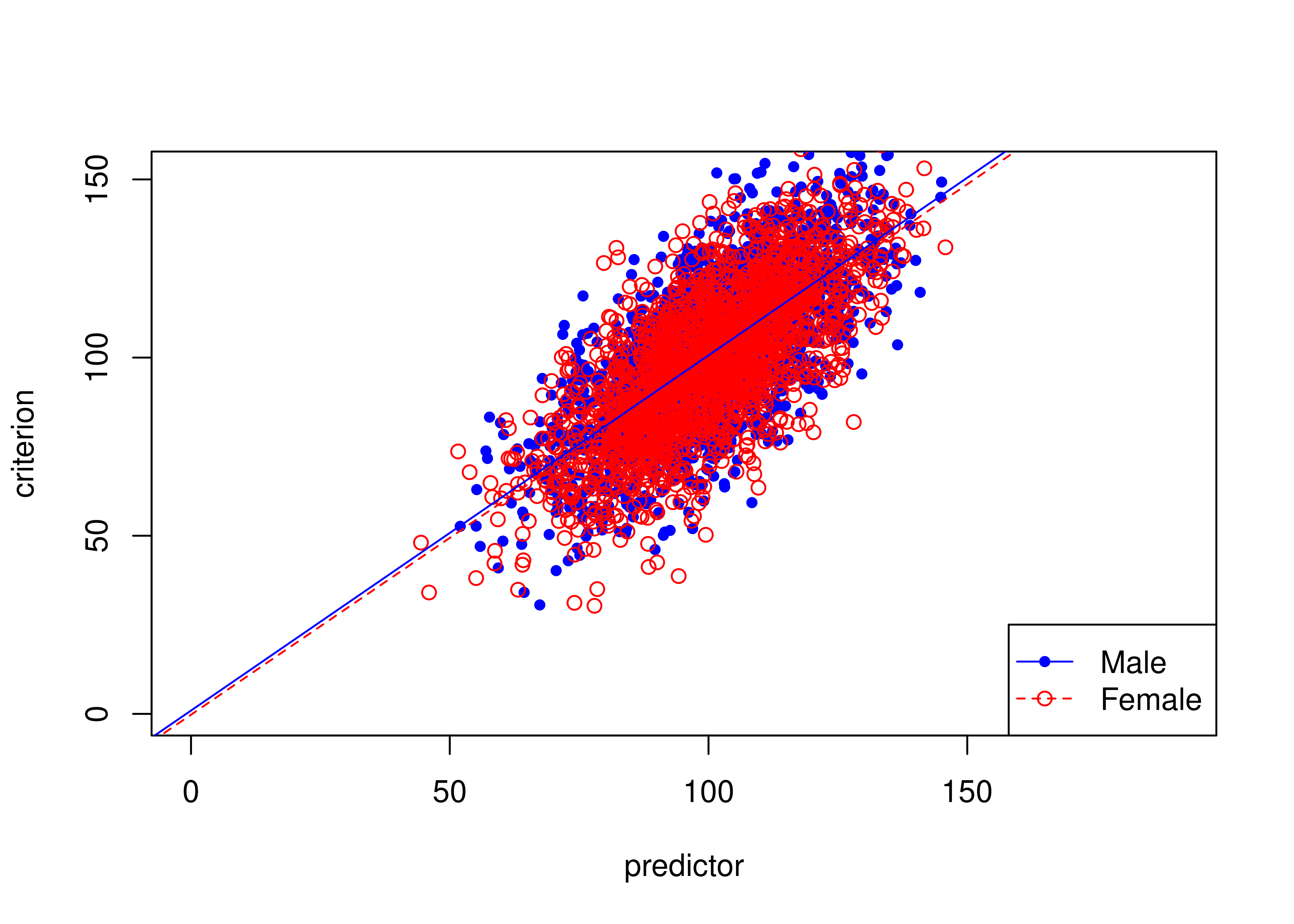

Figure 16.19: Unbiased Test Where Males and Females Have Equal Means on Predictor and Criterion.

16.7.2 Unbiased test where females have higher means than males on predictor and criterion

Figure 16.20 depicts an example of an unbiased test where females have higher means than males on the predictor and criterion. The test is unbiased because there are no differences in the regression lines (of predictor predicting criterion) between males and females.

Code

summary(lm(
  unbiasedCriterion2 ~ unbiasedPredictor2 + group + unbiasedPredictor2:group,
  data = mydataBias))

Call:
lm(formula = unbiasedCriterion2 ~ unbiasedPredictor2 + group + 
    unbiasedPredictor2:group, data = mydataBias)

Residuals:
    Min      1Q  Median      3Q     Max 
-47.302  -9.989   0.010   9.860  53.791 

Coefficients:
                               Estimate Std. Error t value Pr(>|t|)    
(Intercept)                    -1.29332    1.57773  -0.820    0.412    
unbiasedPredictor2              1.02006    0.02218  46.000   <2e-16 ***
groupfemale                     1.21294    3.28319   0.369    0.712    
unbiasedPredictor2:groupfemale -0.01501    0.03125  -0.480    0.631    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 14.81 on 3919 degrees of freedom
  (77 observations deleted due to missingness)
Multiple R-squared:  0.8412,    Adjusted R-squared:  0.8411 
F-statistic:  6921 on 3 and 3919 DF,  p-value: < 2.2e-16

Code

plot(
  unbiasedCriterion2 ~ unbiasedPredictor2,
  data = mydataBias,
  xlim = c(
    0, 
    max(c(
      mydataBias$unbiasedCriterion2,
      mydataBias$unbiasedPredictor2),
      na.rm = TRUE)),
  ylim = c(
    0, 
    max(c(
      mydataBias$criterion1,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$unbiasedPredictor2[which(mydataBias$group == "male")],
  mydataBias$unbiasedCriterion2[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$unbiasedPredictor2[which(mydataBias$group == "female")],
  mydataBias$unbiasedCriterion2[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  unbiasedCriterion2 ~ unbiasedPredictor2,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  unbiasedCriterion2 ~ unbiasedPredictor2,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))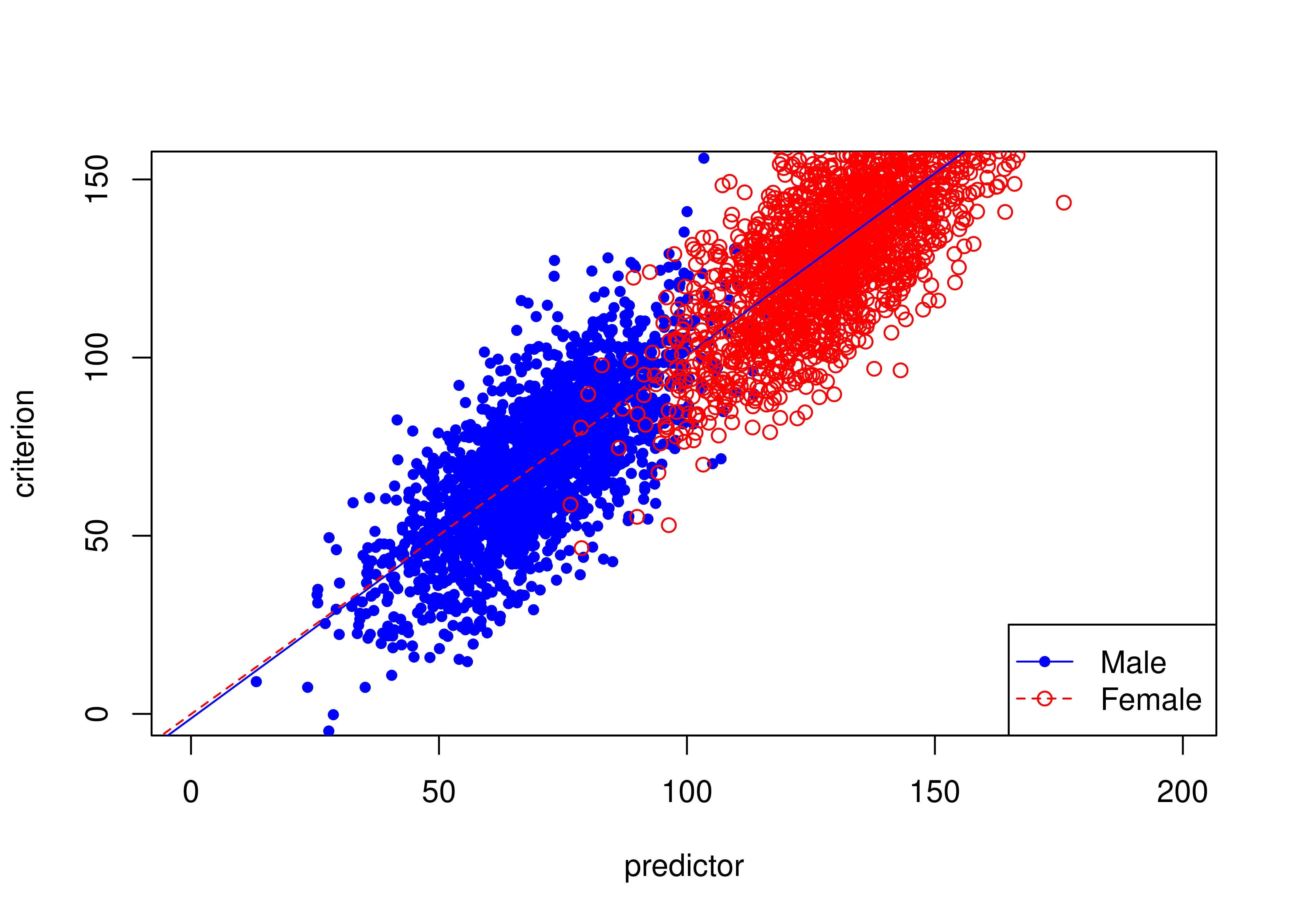

Figure 16.20: Unbiased Test Where Females Have Higher Means Than Males on Predictor and Criterion.

16.7.3 Unbiased test where males have higher means than females on predictor and criterion

Figure 16.21 depicts an example of an unbiased test where males have higher means than females on the predictor and criterion. The test is unbiased because there are no differences in the regression lines (of predictor predicting criterion) between males and females.

Code

summary(lm(
  unbiasedCriterion3 ~ unbiasedPredictor3 + group + unbiasedPredictor3:group,
  data = mydataBias))

Call:
lm(formula = unbiasedCriterion3 ~ unbiasedPredictor3 + group + 
    unbiasedPredictor3:group, data = mydataBias)

Residuals:
    Min      1Q  Median      3Q     Max 
-48.613 -10.115  -0.068   9.598  57.126 

Coefficients:
                               Estimate Std. Error t value Pr(>|t|)    
(Intercept)                    -1.68352    2.84985  -0.591    0.555    
unbiasedPredictor3              1.01072    0.02179  46.375   <2e-16 ***
groupfemale                     1.42842    3.26227   0.438    0.662    
unbiasedPredictor3:groupfemale -0.01187    0.03109  -0.382    0.703    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 14.82 on 3916 degrees of freedom
  (80 observations deleted due to missingness)
Multiple R-squared:  0.8376,    Adjusted R-squared:  0.8375 
F-statistic:  6732 on 3 and 3916 DF,  p-value: < 2.2e-16

Code

plot(
  unbiasedCriterion3 ~ unbiasedPredictor3,
  data = mydataBias,
  xlim = c(
    0,
    max(c(
      mydataBias$unbiasedCriterion3,
      mydataBias$unbiasedPredictor3),
      na.rm = TRUE)),
  ylim = c(0, max(c(
    mydataBias$criterion1,
    mydataBias$predictor),
    na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$unbiasedPredictor3[which(mydataBias$group == "male")],
  mydataBias$unbiasedCriterion3[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$unbiasedPredictor3[which(mydataBias$group == "female")],
  mydataBias$unbiasedCriterion3[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  unbiasedCriterion3 ~ unbiasedPredictor3,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  unbiasedCriterion3 ~ unbiasedPredictor3,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))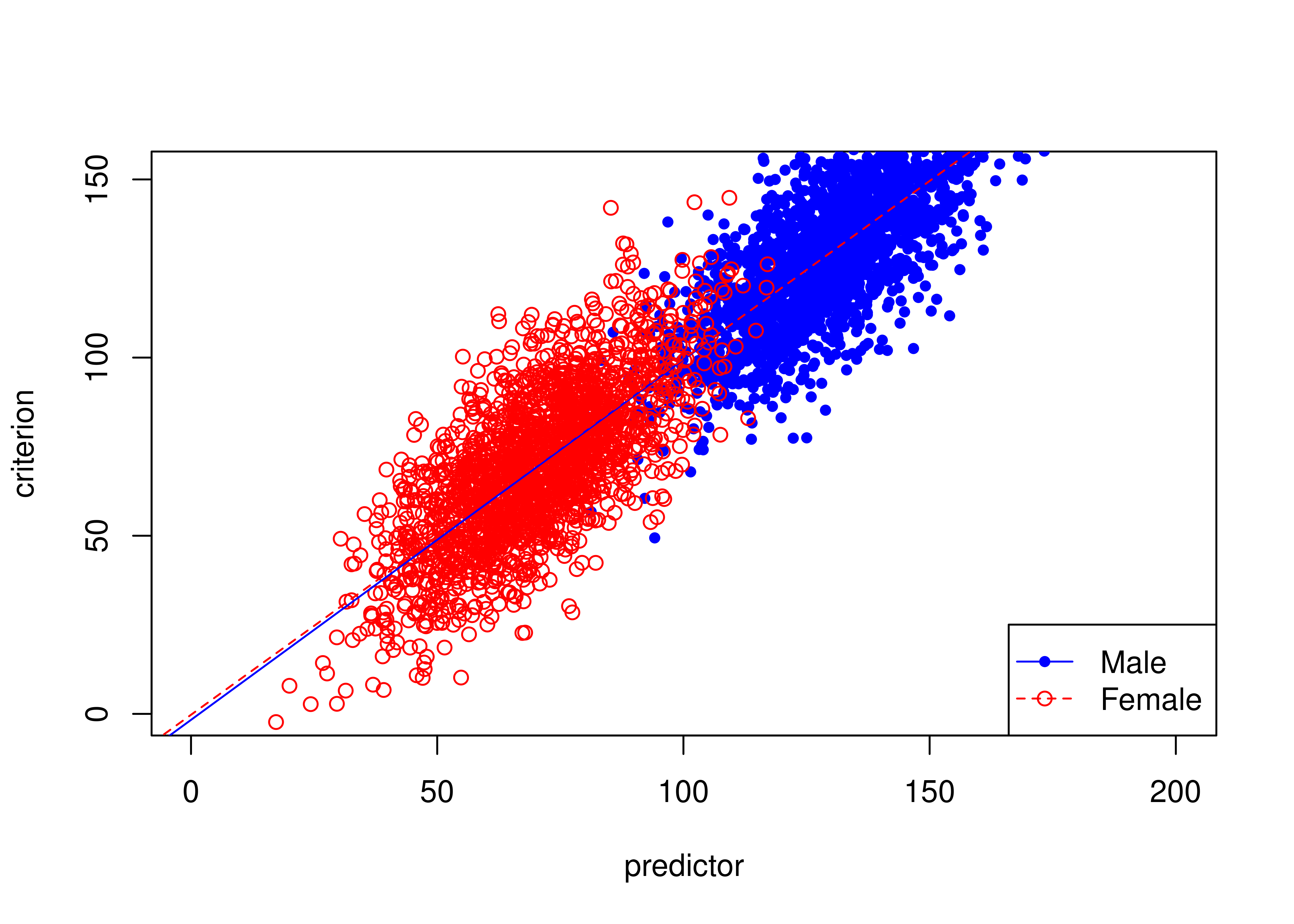

Figure 16.21: Unbiased Test Where Males Have Higher Means Than Females on Predictor and Criterion.

16.8 Predictive Bias: Different Regression Lines

16.8.1 Example of unbiased prediction (no differences in intercepts or slopes)

Figure 16.22 depicts an example of an unbiased test where males and females have equal means on the predictor and criterion. The test is unbiased because there are no differences in the regression lines (of predictor predicting criterion1) between males and females.

Code

summary(lm(
  criterion1 ~ predictor + group + predictor:group,
  data = mydataBias))

Call:
lm(formula = criterion1 ~ predictor + group + predictor:group, 
    data = mydataBias)

Residuals:
    Min      1Q  Median      3Q     Max 
-18.831  -3.338   0.004   3.330  19.335 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -0.264357   0.747269  -0.354    0.724    
predictor              0.701726   0.007370  95.207   <2e-16 ***
groupfemale           -0.515860   1.059267  -0.487    0.626    
predictor:groupfemale  0.006002   0.010476   0.573    0.567    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 4.952 on 3908 degrees of freedom
  (88 observations deleted due to missingness)
Multiple R-squared:  0.8225,    Adjusted R-squared:  0.8223 
F-statistic:  6035 on 3 and 3908 DF,  p-value: < 2.2e-16

Code

plot(
  criterion1 ~ predictor,
  data = mydataBias,
  xlim = c(
    0,
    max(c(
      mydataBias$criterion1,
      mydataBias$predictor),
      na.rm = TRUE)),
  ylim = c(
    0, 
    max(c(
      mydataBias$criterion1,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$predictor[which(mydataBias$group == "male")],
  mydataBias$criterion1[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$predictor[which(mydataBias$group == "female")],
  mydataBias$criterion1[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  criterion1 ~ predictor,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  criterion1 ~ predictor,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))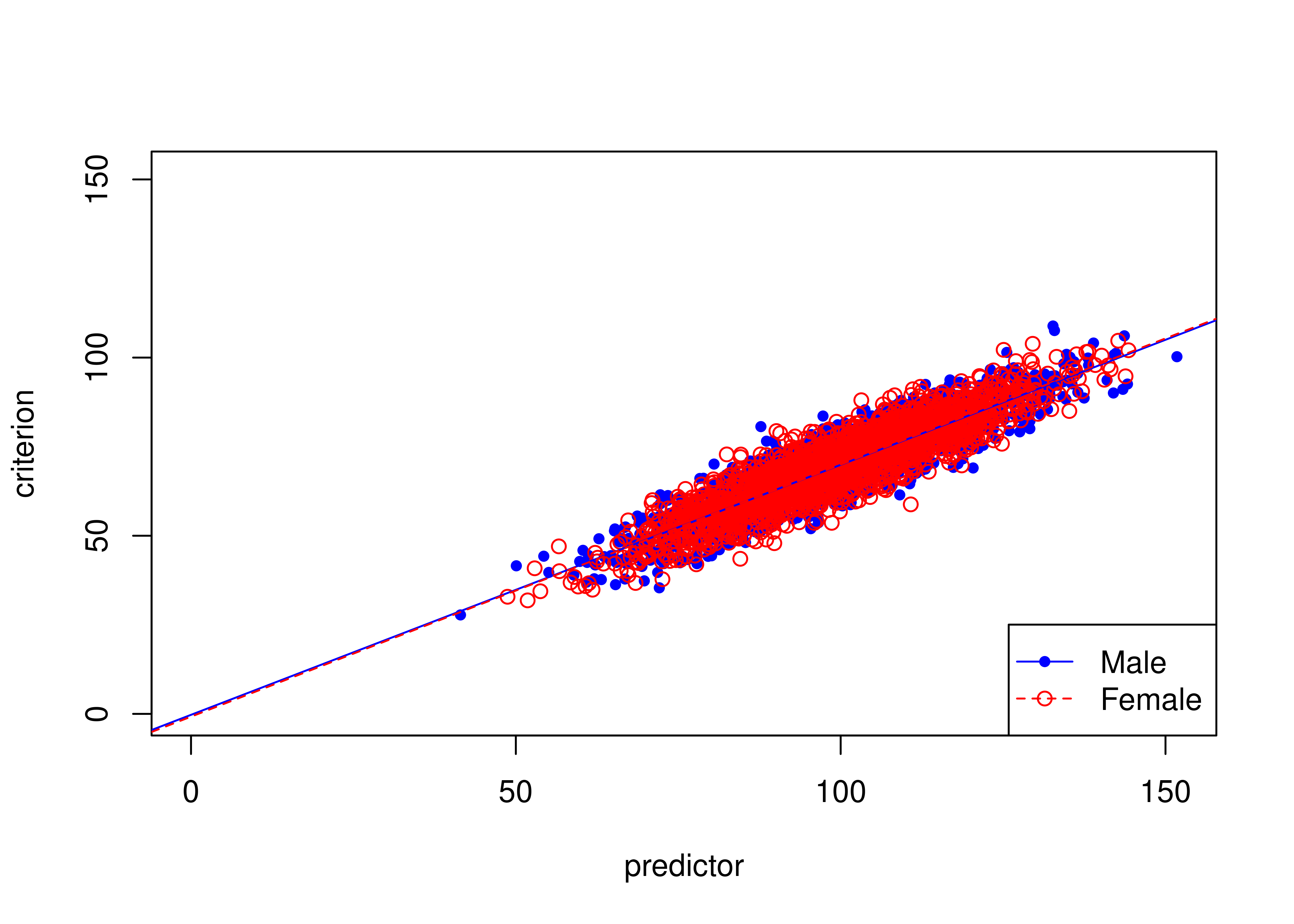

Figure 16.22: Example of Unbiased Prediction (No Differences in Intercepts or Slopes Between Males and Females).

16.8.2 Example of intercept bias

Figure 16.23 depicts an example of a biased test due to intercept bias. There are differences in the intercepts of the regression lines (of predictor predicting criterion2) between males and females: males have a higher intercept than females. That is, the same score on the predictor results in higher predictions for males than females.

Code

summary(lm(
  criterion2 ~ predictor + group + predictor:group,
  data = mydataBias))

Call:
lm(formula = criterion2 ~ predictor + group + predictor:group, 
    data = mydataBias)

Residuals:
     Min       1Q   Median       3Q      Max 
-18.6853  -3.4153  -0.0385   3.3979  18.0864 

Coefficients:
                        Estimate Std. Error t value Pr(>|t|)    
(Intercept)            10.054048   0.760084  13.228   <2e-16 ***
predictor               0.697987   0.007499  93.075   <2e-16 ***
groupfemale           -10.288893   1.074168  -9.578   <2e-16 ***
predictor:groupfemale   0.004748   0.010625   0.447    0.655    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.037 on 3913 degrees of freedom
  (83 observations deleted due to missingness)
Multiple R-squared:  0.8452,    Adjusted R-squared:  0.8451 
F-statistic:  7124 on 3 and 3913 DF,  p-value: < 2.2e-16

Code

plot(
  criterion2 ~ predictor,
  data = mydataBias,
  xlim = c(
    0,
    max(c(
      mydataBias$criterion2,
      mydataBias$predictor), na.rm = TRUE)),
  ylim = c(
    0,
    max(c(
      mydataBias$criterion2,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$predictor[which(mydataBias$group == "male")],
  mydataBias$criterion2[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$predictor[which(mydataBias$group == "female")],
  mydataBias$criterion2[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  criterion2 ~ predictor,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  criterion2 ~ predictor,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))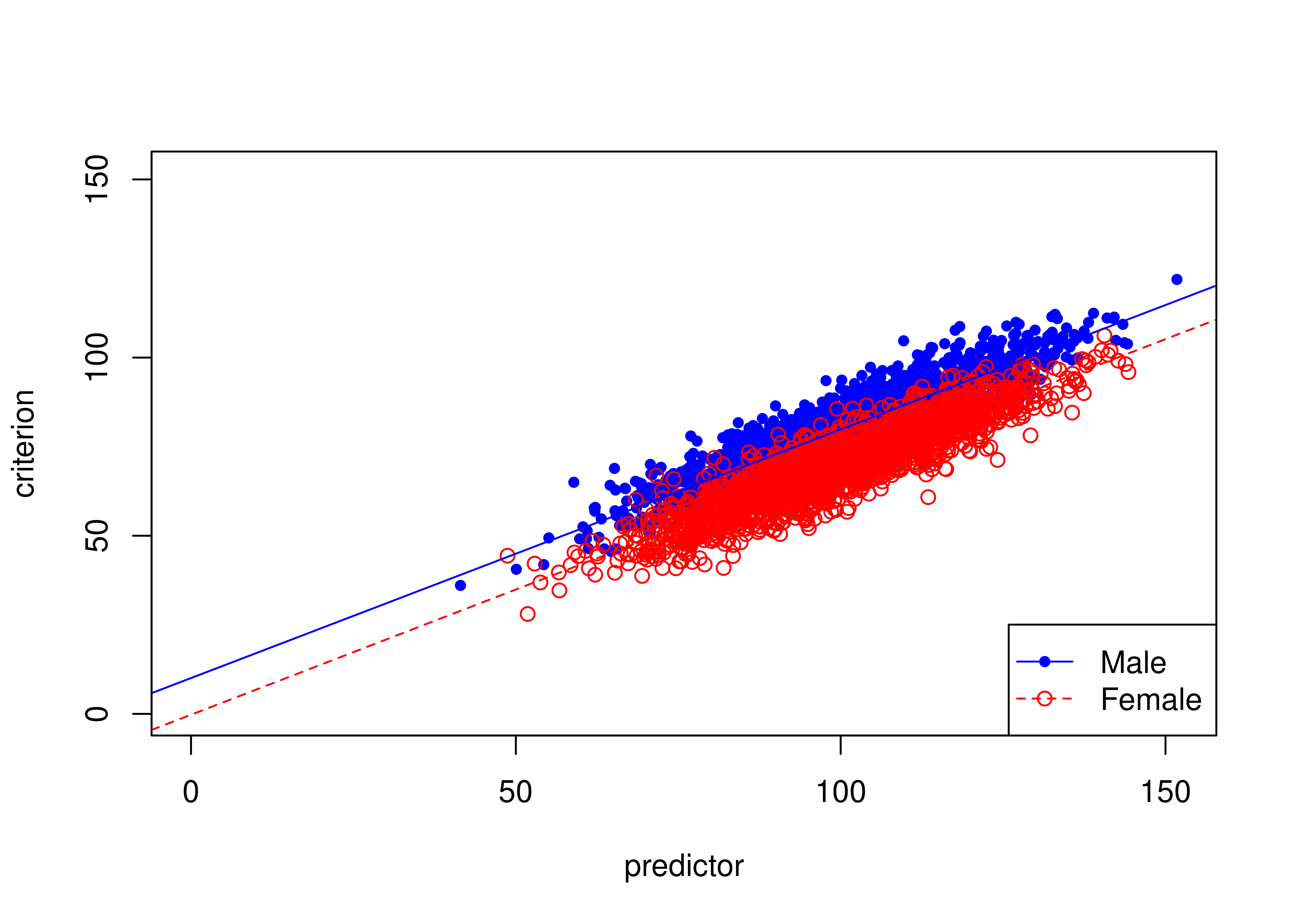

Figure 16.23: Example of Intercept Bias in Prediction (Different Intercepts Between Males and Females).

16.8.3 Example of slope bias

Figure 16.24 depicts an example of a biased test due to slope bias. There are differences in the slopes of the regression lines (of predictor predicting criterion3) between males and females: males have a higher slope than females. That is, scores have stronger predictive validity for males than females.

Code

summary(lm(
  criterion3 ~ predictor + group + predictor:group,
  data = mydataBias))

Call:
lm(formula = criterion3 ~ predictor + group + predictor:group, 
    data = mydataBias)

Residuals:
     Min       1Q   Median       3Q      Max 
-18.3183  -3.3715   0.0256   3.3844  19.3484 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -1.041940   0.757914  -1.375    0.169    
predictor              0.708670   0.007475  94.804   <2e-16 ***
groupfemale            1.478534   1.074064   1.377    0.169    
predictor:groupfemale -0.413233   0.010621 -38.907   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.031 on 3927 degrees of freedom
  (69 observations deleted due to missingness)
Multiple R-squared:  0.9489,    Adjusted R-squared:  0.9489 
F-statistic: 2.432e+04 on 3 and 3927 DF,  p-value: < 2.2e-16

Code

plot(
  criterion3 ~ predictor,
  data = mydataBias,
  xlim = c(
    0,
    max(c(
      mydataBias$criterion3,
      mydataBias$predictor),
      na.rm = TRUE)),
  ylim = c(
    0,
    max(c(
      mydataBias$criterion3,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$predictor[which(mydataBias$group == "male")],
  mydataBias$criterion3[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$predictor[which(mydataBias$group == "female")],
  mydataBias$criterion3[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  criterion3 ~ predictor,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  criterion3 ~ predictor,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))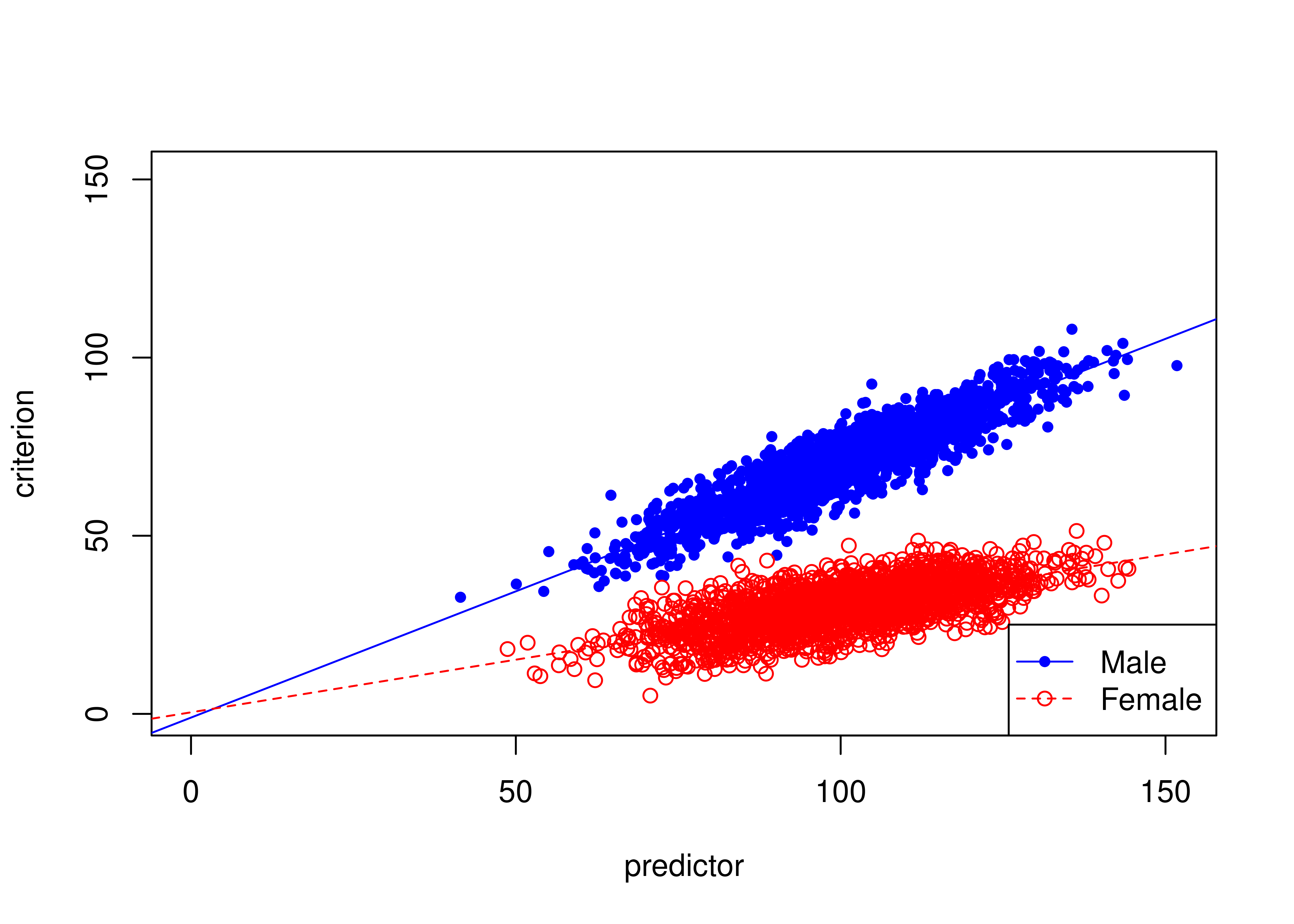

Figure 16.24: Example of Slope Bias in Prediction (Different Slopes Between Males And Females).

16.8.4 Example of intercept and slope bias

Figure 16.25 depicts an example of a biased test due to intercept and slope bias. There are differences in the intercepts and slopes of the regression lines (of predictor predicting criterion4) between males and females: males have a higher slope than females. That is, scores have stronger predictive validity for males than females. Females have a higher intercept than males. That is, at lower scores, the same score on the predictor results in higher predictions for females than males; at higher scores on the predictor, the same score results in higher predictions for males than females.

Code

summary(lm(
  criterion4 ~ predictor + group + predictor:group,
  data = mydataBias))

Call:
lm(formula = criterion4 ~ predictor + group + predictor:group, 
    data = mydataBias)

Residuals:
     Min       1Q   Median       3Q      Max 
-18.2805  -3.4400   0.0269   3.3199  17.8824 

Coefficients:
                       Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -0.276228   0.767080   -0.36    0.719    
predictor              0.702178   0.007565   92.81   <2e-16 ***
groupfemale           29.156167   1.086254   26.84   <2e-16 ***
predictor:groupfemale -0.392016   0.010743  -36.49   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 5.099 on 3930 degrees of freedom
  (66 observations deleted due to missingness)
Multiple R-squared:  0.7843,    Adjusted R-squared:  0.7842 
F-statistic:  4764 on 3 and 3930 DF,  p-value: < 2.2e-16

Code

plot(
  criterion4 ~ predictor,
  data = mydataBias,
  xlim = c(
    0,
    max(c(
      mydataBias$criterion4,
      mydataBias$predictor),
      na.rm = TRUE)),
  ylim = c(
    0,
    max(c(
      mydataBias$criterion4,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$predictor[which(mydataBias$group == "male")],
  mydataBias$criterion4[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(
  mydataBias$predictor[which(mydataBias$group == "female")],
  mydataBias$criterion4[which(mydataBias$group == "female")],
  pch = 1,
  col = "red")
abline(lm(
  criterion4 ~ predictor,
  data = mydataBias[which(mydataBias$group == "male"),]),
  lty = 1,
  col = "blue")
abline(lm(
  criterion4 ~ predictor,
  data = mydataBias[which(mydataBias$group == "female"),]),
  lty = 2,
  col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))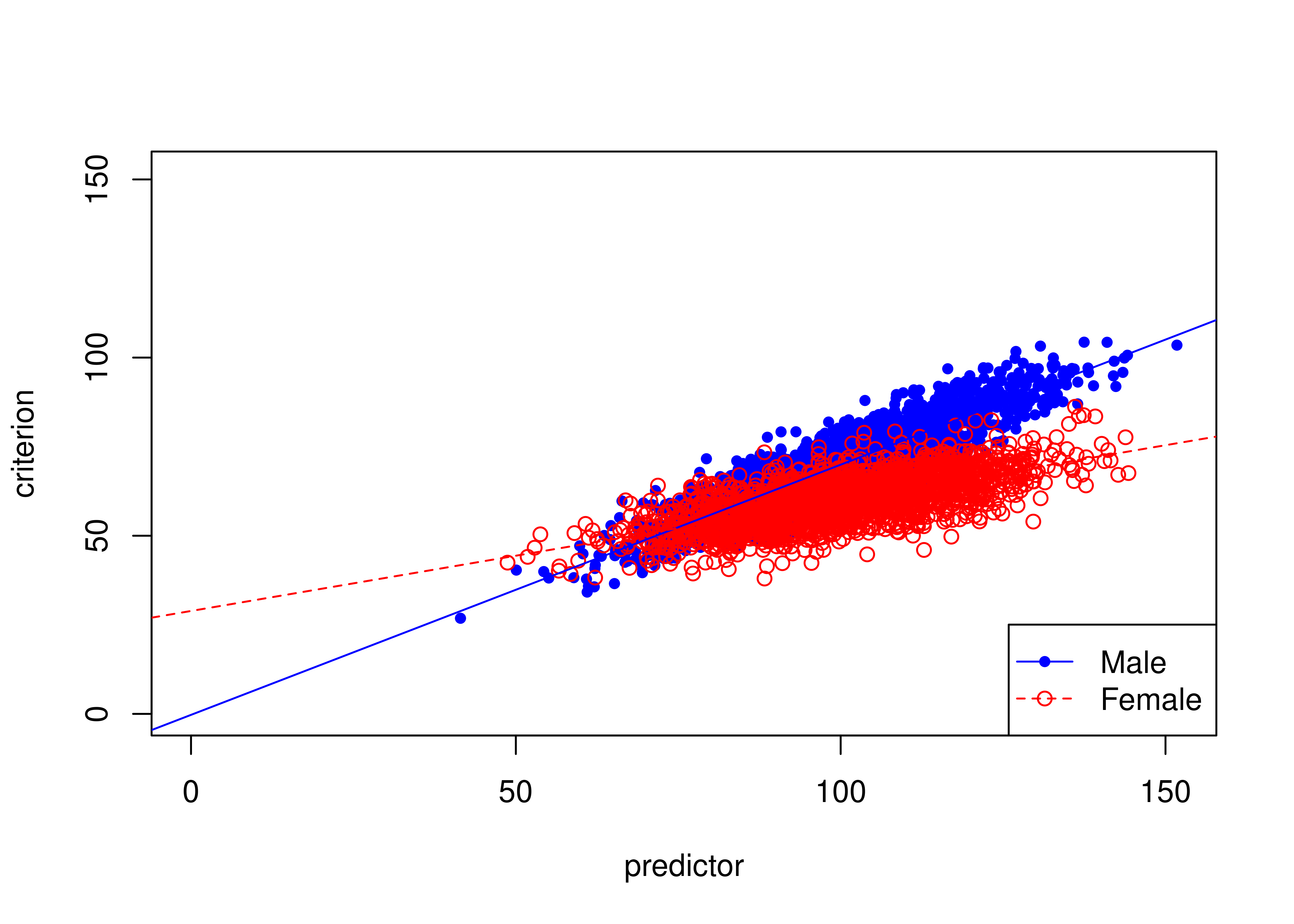

Figure 16.25: Example of Intercept And Slope Bias in Prediction (Different Intercepts and Slopes Between Males and Females).

16.8.5 Example of different measurement reliability/error across groups

In the example depicted in Figure 16.26, there are differences in the measurement reliability/error on the criterion between males and females: males’ scores have a lower reliability (higher measurement error) on the criterion than females’ scores. That is, we are more confident about a female’s level on the criterion given a particular score on the predictor than we are about a male’s level on the criterion given a particular score on the predictor.

Code

summary(lm(
  criterion5 ~ predictor + group + predictor:group,
  data = mydataBias))

Call:
lm(formula = criterion5 ~ predictor + group + predictor:group, 
    data = mydataBias)

Residuals:
     Min       1Q   Median       3Q      Max 
-109.295   -7.065    0.077    6.836  108.428 

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)    
(Intercept)           -9.28386    3.32617  -2.791  0.00528 ** 
predictor              0.79172    0.03280  24.136  < 2e-16 ***
groupfemale            9.12452    4.70470   1.939  0.05252 .  
predictor:groupfemale -0.09083    0.04654  -1.952  0.05102 .  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 22.03 on 3920 degrees of freedom
  (76 observations deleted due to missingness)
Multiple R-squared:  0.2087,    Adjusted R-squared:  0.2081 
F-statistic: 344.6 on 3 and 3920 DF,  p-value: < 2.2e-16

Code

plot(
  criterion5 ~ predictor,
  data = mydataBias,
  xlim = c(
    0,
    max(c(mydataBias$criterion5,
          mydataBias$predictor),
        na.rm = TRUE)),
  ylim = c(
    0, 
    max(c(
      mydataBias$criterion5,
      mydataBias$predictor),
      na.rm = TRUE)),
  type = "n",
  xlab = "predictor",
  ylab = "criterion")
points(
  mydataBias$predictor[which(mydataBias$group == "male")],
  mydataBias$criterion5[which(mydataBias$group == "male")],
  pch = 20,
  col = "blue")
points(mydataBias$predictor[which(mydataBias$group == "female")],
       mydataBias$criterion5[which(mydataBias$group == "female")],
       pch = 1,
       col = "red")
abline(lm(criterion5 ~ predictor,
          data = mydataBias[which(mydataBias$group == "male"),]),
       lty = 1,
       col = "blue")
abline(lm(criterion5 ~ predictor,
          data = mydataBias[which(mydataBias$group == "female"),]),
       lty = 2,
       col = "red")
legend(
  "bottomright",
  c("Male","Female"),
  lty = c(1,2),
  pch = c(20,1),
  col = c("blue","red"))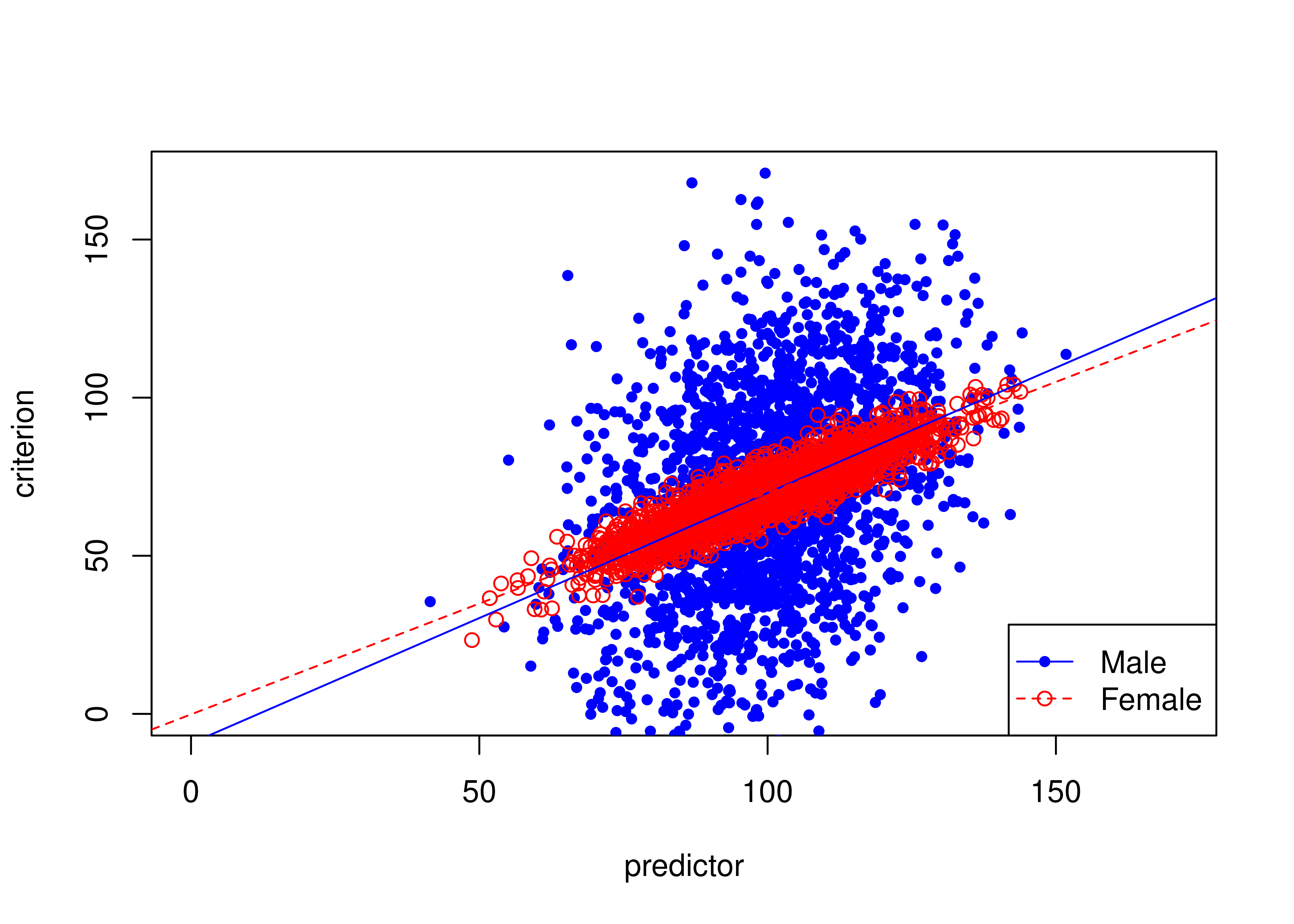

Figure 16.26: Example of Different Measurement Reliability/Error Across Groups.

16.9 Differential Item Functioning (DIF)

Differential item functioning (DIF) indicates that one or more items functions differently across groups. That is, one or more of the item parameters for an item differs across groups. For instance, the severity or discrimination of an item could be higher in one group compared to another group. If an item functions differently across groups, it can lead to biased scores for particular groups. Thus, when observing group differences in level on the measure or group differences in the measure’s association with other measures, it is unclear whether the observed group differences reflect true group differences or differences in the functioning of the measure across groups.

For instance, consider an item such as “disobedience to authority”, which is thought to reflect externalizing behavior in childhood. However, in adulthood, disobedience to authority could reflect prosocial functions, such as protesting against societally unjust actions, and may show weaker construct validity with respect to externalizing problems, as operationalized by a weaker discrimination coefficient in adulthood than in childhood. Tests of differential item functioning are equivalent to tests of measurement invariance.

Approaches to addressing DIF are described in Section 16.5.1. If we identify that an item shows non-negligible DIF, we have three primary options (described above): (1) drop the item for both groups, (2) drop the item for one group but keep it for the other group, or (3) freely estimate the parameters (discrimination and difficulty) for the item across groups.

Tests of DIF were conducted using the mirt package (Chalmers, 2020).

16.9.1 Item Descriptive Statistics

Code

itemstats(
  data = cnlsy[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7")],
  group = cnlsy$sex,
  ts.tables = TRUE)

$female
$female$overall
 N.complete    N mean_total.score sd_total.score ave.r  sd.r alpha SEM.alpha
       1620 5641            2.554          2.132 0.255 0.083 0.681     1.203

$female$itemstats
                      N  mean    sd total.r total.r_if_rm alpha_if_rm
bpi_antisocialT1_1 1928 0.538 0.587   0.662         0.456       0.626
bpi_antisocialT1_2 1925 0.278 0.510   0.648         0.471       0.624
bpi_antisocialT1_3 1925 0.456 0.654   0.625         0.376       0.657
bpi_antisocialT1_4 1933 0.113 0.355   0.523         0.384       0.654
bpi_antisocialT1_5 1649 0.186 0.431   0.594         0.438       0.637
bpi_antisocialT1_6 1658 0.103 0.345   0.572         0.446       0.643
bpi_antisocialT1_7 1944 0.834 0.639   0.553         0.292       0.683

$female$proportions
                       0     1     2    NA
bpi_antisocialT1_1 0.174 0.151 0.016 0.658
bpi_antisocialT1_2 0.257 0.075 0.010 0.659
bpi_antisocialT1_3 0.216 0.094 0.031 0.659
bpi_antisocialT1_4 0.308 0.030 0.004 0.657
bpi_antisocialT1_5 0.243 0.044 0.005 0.708
bpi_antisocialT1_6 0.268 0.023 0.004 0.706
bpi_antisocialT1_7 0.104 0.194 0.046 0.655

$female$total.score_frequency
       0   1   2   3   4  5  6  7  8  9 10 11 12 13
Freq 217 364 349 283 166 91 67 38 12 10 11  4  4  4

$female$total.score_means
                          0        1        2
bpi_antisocialT1_1 1.354919 3.339237 7.216867
bpi_antisocialT1_2 1.846343 4.173789 8.192308
bpi_antisocialT1_3 1.593417 3.846682 5.406667
bpi_antisocialT1_4 2.204952 5.090278 9.045455
bpi_antisocialT1_5 2.010386 4.946721 7.892857
bpi_antisocialT1_6 2.189959 5.701613 9.227273
bpi_antisocialT1_7 1.004357 2.778970 4.746725

$female$total.score_sds
                          0        1        2
bpi_antisocialT1_1 1.262270 1.668474 2.763209
bpi_antisocialT1_2 1.480206 1.809814 2.664498
bpi_antisocialT1_3 1.329902 1.837884 2.783211
bpi_antisocialT1_4 1.743521 2.280698 2.802673
bpi_antisocialT1_5 1.566126 2.196431 3.258485
bpi_antisocialT1_6 1.684322 2.215906 2.844072
bpi_antisocialT1_7 1.232733 1.798814 2.475591


$male
$male$overall
 N.complete    N mean_total.score sd_total.score ave.r  sd.r alpha SEM.alpha
       1645 5891             3.16          2.385 0.266 0.081 0.703       1.3

$male$itemstats
                      N  mean    sd total.r total.r_if_rm alpha_if_rm
bpi_antisocialT1_1 1948 0.615 0.585   0.634         0.449       0.660
bpi_antisocialT1_2 1947 0.372 0.559   0.655         0.485       0.650
bpi_antisocialT1_3 1949 0.520 0.668   0.582         0.346       0.692
bpi_antisocialT1_4 1948 0.233 0.486   0.596         0.441       0.666
bpi_antisocialT1_5 1676 0.367 0.547   0.627         0.454       0.662
bpi_antisocialT1_6 1688 0.177 0.446   0.556         0.406       0.675
bpi_antisocialT1_7 1962 0.834 0.646   0.582         0.357       0.687

$male$proportions
                       0     1     2    NA
bpi_antisocialT1_1 0.145 0.168 0.017 0.669
bpi_antisocialT1_2 0.220 0.097 0.013 0.669
bpi_antisocialT1_3 0.191 0.107 0.033 0.669
bpi_antisocialT1_4 0.263 0.058 0.010 0.669
bpi_antisocialT1_5 0.190 0.085 0.010 0.715
bpi_antisocialT1_6 0.243 0.035 0.008 0.713
bpi_antisocialT1_7 0.102 0.185 0.046 0.667

$male$total.score_frequency
       0   1   2   3   4   5   6  7  8  9 10 11 12 13 14
Freq 163 294 310 259 208 144 104 74 40 25  9  7  5  1  2

$male$total.score_means
                          0        1        2
bpi_antisocialT1_1 1.622478 3.944056 7.397849
bpi_antisocialT1_2 2.134191 4.767821 8.106061
bpi_antisocialT1_3 2.016754 4.400763 5.819277
bpi_antisocialT1_4 2.484091 5.539286 8.177778
bpi_antisocialT1_5 2.174111 4.817073 7.910714
bpi_antisocialT1_6 2.616762 5.810680 8.093023
bpi_antisocialT1_7 1.412500 3.375679 5.782787

$male$total.score_sds
                          0        1        2
bpi_antisocialT1_1 1.515237 1.982218 2.454542
bpi_antisocialT1_2 1.678482 1.955386 2.437709
bpi_antisocialT1_3 1.654589 2.069463 2.774973
bpi_antisocialT1_4 1.845772 2.119687 2.534210
bpi_antisocialT1_5 1.709715 2.047072 2.725481
bpi_antisocialT1_6 1.911288 2.181537 2.982600
bpi_antisocialT1_7 1.522500 1.906515 2.652344

16.9.2 Unconstrained Model

16.9.2.1 Fit Model

Code

unconstrainedModel <- multipleGroup(
  data = cnlsy[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7")],
  model = 1,
  group = cnlsy$sex,
  SE = TRUE)

16.9.2.2 Model Summary

Items that appear to differ:

• items 5 and 6 are more discriminating (\(a\) parameter) among females than males
• item 4 has higher difficulty/severity (\(b_1\) and \(b_2\) parameters) among males than females

Code

summary(unconstrainedModel)

----------
GROUP: female 
                      F1    h2
bpi_antisocialT1_1 0.698 0.487
bpi_antisocialT1_2 0.706 0.499
bpi_antisocialT1_3 0.532 0.283
bpi_antisocialT1_4 0.683 0.466
bpi_antisocialT1_5 0.763 0.582
bpi_antisocialT1_6 0.838 0.702
bpi_antisocialT1_7 0.429 0.184

SS loadings:  3.202 
Proportion Var:  0.457 

Factor correlations: 

   F1
F1  1

----------
GROUP: male 
                      F1    h2
bpi_antisocialT1_1 0.663 0.440
bpi_antisocialT1_2 0.736 0.542
bpi_antisocialT1_3 0.531 0.282
bpi_antisocialT1_4 0.713 0.508
bpi_antisocialT1_5 0.691 0.477
bpi_antisocialT1_6 0.702 0.492
bpi_antisocialT1_7 0.507 0.257

SS loadings:  2.999 
Proportion Var:  0.428 

Factor correlations: 

   F1
F1  1

Code

coef(unconstrainedModel,
     simplify = TRUE,
     IRTpars = TRUE)

$female
$items
                       a     b1    b2
bpi_antisocialT1_1 1.657  0.029 2.451
bpi_antisocialT1_2 1.697  0.953 2.763
bpi_antisocialT1_3 1.069  0.650 2.585
bpi_antisocialT1_4 1.590  1.895 3.465
bpi_antisocialT1_5 2.008  1.281 2.936
bpi_antisocialT1_6 2.614  1.625 2.770
bpi_antisocialT1_7 0.807 -1.184 2.583

$means
F1 
 0 

$cov
   F1
F1  1


$male
$items
                       a     b1    b2
bpi_antisocialT1_1 1.507 -0.238 2.505
bpi_antisocialT1_2 1.853  0.582 2.455
bpi_antisocialT1_3 1.067  0.384 2.480
bpi_antisocialT1_4 1.729  1.165 2.765
bpi_antisocialT1_5 1.625  0.635 2.757
bpi_antisocialT1_6 1.677  1.494 2.873
bpi_antisocialT1_7 1.002 -0.986 2.143

$means
F1 
 0 

$cov
   F1
F1  1

16.9.3 Constrained Model

Constrain item parameters to be equal across groups (to use as baseline model for identifying DIF).

16.9.3.1 Fit Model

Code

constrainedModel <- multipleGroup(
  data = cnlsy[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7")],
  model = 1,
  group = cnlsy$sex,
  invariance = c(c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7"),
    "free_means", "free_var"),
  SE = TRUE)

16.9.3.2 Model Summary

Code

summary(constrainedModel)

----------
GROUP: female 
                      F1    h2
bpi_antisocialT1_1 0.657 0.431
bpi_antisocialT1_2 0.707 0.500
bpi_antisocialT1_3 0.512 0.262
bpi_antisocialT1_4 0.701 0.491
bpi_antisocialT1_5 0.733 0.538
bpi_antisocialT1_6 0.765 0.585
bpi_antisocialT1_7 0.440 0.193

SS loadings:  3 
Proportion Var:  0.429 

Factor correlations: 

   F1
F1  1

----------
GROUP: male 
                      F1    h2
bpi_antisocialT1_1 0.672 0.452
bpi_antisocialT1_2 0.722 0.521
bpi_antisocialT1_3 0.527 0.278
bpi_antisocialT1_4 0.716 0.512
bpi_antisocialT1_5 0.747 0.559
bpi_antisocialT1_6 0.778 0.605
bpi_antisocialT1_7 0.455 0.207

SS loadings:  3.134 
Proportion Var:  0.448 

Factor correlations: 

   F1
F1  1

Code

coef(
  constrainedModel,
  simplify = TRUE,
  IRTpars = TRUE)

$female
$items
                       a     b1    b2
bpi_antisocialT1_1 1.482  0.078 2.798
bpi_antisocialT1_2 1.701  0.973 2.892
bpi_antisocialT1_3 1.013  0.726 2.844
bpi_antisocialT1_4 1.673  1.688 3.278
bpi_antisocialT1_5 1.836  1.135 3.028
bpi_antisocialT1_6 2.020  1.782 3.048
bpi_antisocialT1_7 0.834 -0.967 2.697

$means
F1 
 0 

$cov
   F1
F1  1


$male
$items
                       a     b1    b2
bpi_antisocialT1_1 1.482  0.078 2.798
bpi_antisocialT1_2 1.701  0.973 2.892
bpi_antisocialT1_3 1.013  0.726 2.844
bpi_antisocialT1_4 1.673  1.688 3.278
bpi_antisocialT1_5 1.836  1.135 3.028
bpi_antisocialT1_6 2.020  1.782 3.048
bpi_antisocialT1_7 0.834 -0.967 2.697

$means
  F1 
0.37 

$cov
      F1
F1 1.088

16.9.4 Compare model fit of constrained model to unconstrained model

The constrained model and the unconstrained model are considered “nested” models. The constrained model is nested within the unconstrained model because the unconstrained model includes all of the terms of the constrained model along with additional terms. Model fit of nested models can be compared with a chi-square difference test.

Code

anova(constrainedModel, unconstrainedModel)

The constrained model fits significantly worse than the unconstrained model, which suggests that item parameters differ between males and females.

16.9.5 Identify DIF by iteratively removing constraints from fully constrained model

One way to identify DIF is to iteratively remove constraints from a model in which all parameters are constrained to be the same across groups. Removing constraints allows individual items to have different item parameters across groups, to identify which items yield a significant improvement in model fit when allowing their discrimination and/or severity to differ across groups. Items 1, 3, 4, 5, 6, and 7 showed DIF in discrimination and/or severity, based on a significant chi-square difference test.

16.9.5.1 Items that differ in discrimination and/or severity

Code

difDropItems <- DIF(
  constrainedModel,
  c("a1","d1","d2"),
  scheme = "drop",
  simplify = TRUE)

difDropItems

16.9.5.2 Items that differ in discrimination

Items 1, 3, 4, and 5 showed DIF in discrimination, based on a significant chi-square difference test.

Code

difDropItemsDiscrimination <- DIF(
  constrainedModel,
  c("a1"),
  scheme = "drop",
  simplify = TRUE)

difDropItemsDiscrimination

16.9.5.3 Items that differ in severity

Items 1, 3, 4, 5, and 7 showed DIF in difficulty/severity, based on a significant chi-square difference test.

Code

difDropItemsSeverity <- DIF(
  constrainedModel,
  c("d1","d2"),
  scheme = "drop",
  simplify = TRUE)

difDropItemsSeverity

16.9.6 Identify DIF by iteratively adding constraints to unconstrained model

16.9.6.1 Items that differ in discrimination and/or severity

Another way to identify DIF is to iteratively add constraints to a model in which all parameters are allowed to differ across groups. Adding constraints forces individual items to have the same item parameters across groups, to identify which items yield a significant worsening in model fit when constraining their discrimination and/or severity to be the same across groups. Items 1, 2, 3, 4, 5, and 6 showed DIF in discrimination and/or severity, based on a significant chi-square difference test. The DIF in discrimination and/or severity is depicted in Figure 16.27.

Code

difAddItems <- DIF(
  unconstrainedModel,
  c("a1","d1","d2"),
  scheme = "add",
  simplify = TRUE,
  plotdif = TRUE)

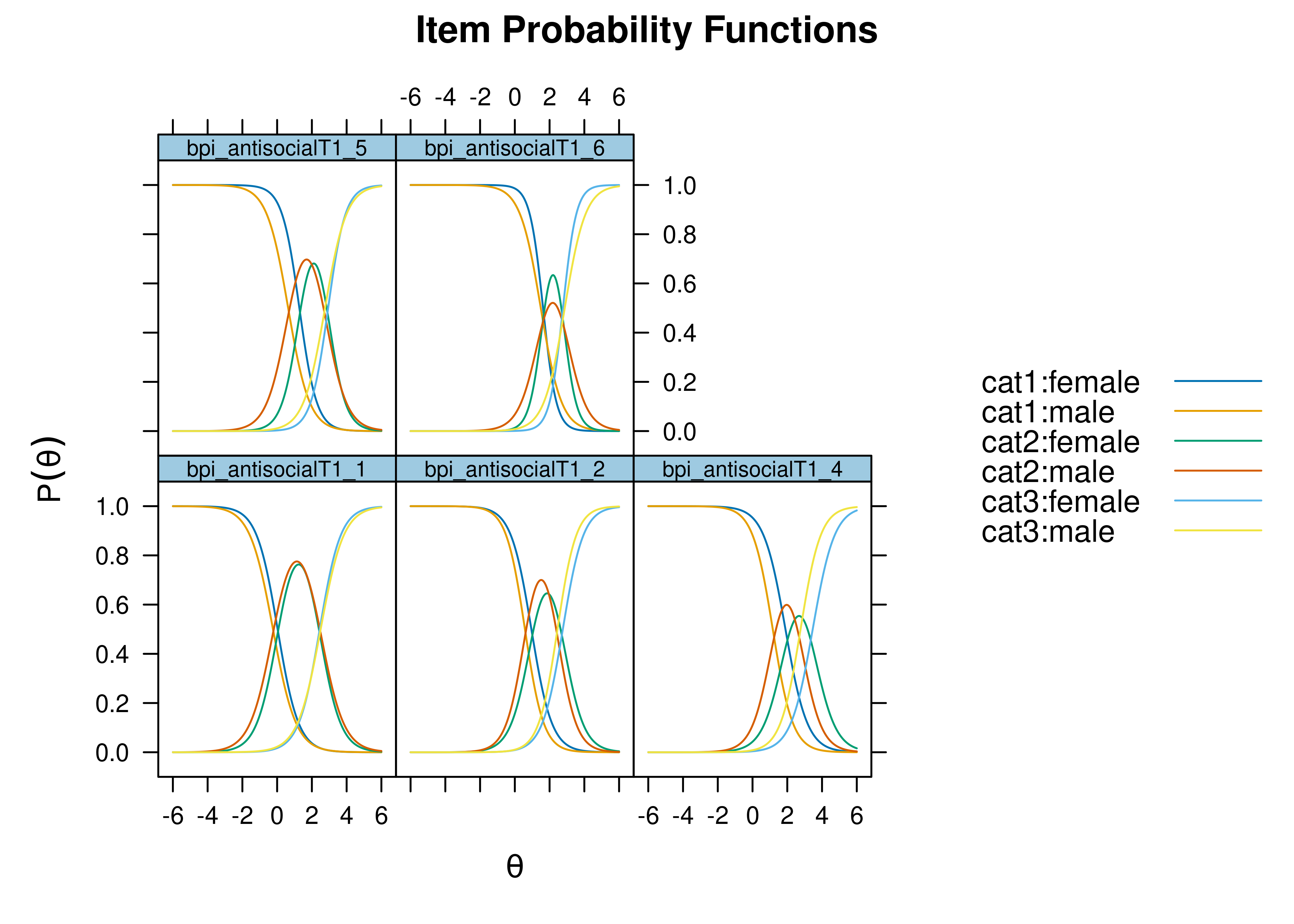
Figure 16.27: Item Probability Functions for Examining Differential Item Functioning in Terms of Discrimination and/or Severity.

Code

difAddItems

16.9.6.2 Items that differ in discrimination

Items 6 and 7 showed DIF in discrimination, based on a significant chi-square difference test. The DIF in discrimination is depicted in Figure 16.28.

Code

difAddItemsDiscrimination <- DIF(
  unconstrainedModel,
  c("a1"),
  scheme = "add",
  simplify = TRUE,
  plotdif = TRUE)

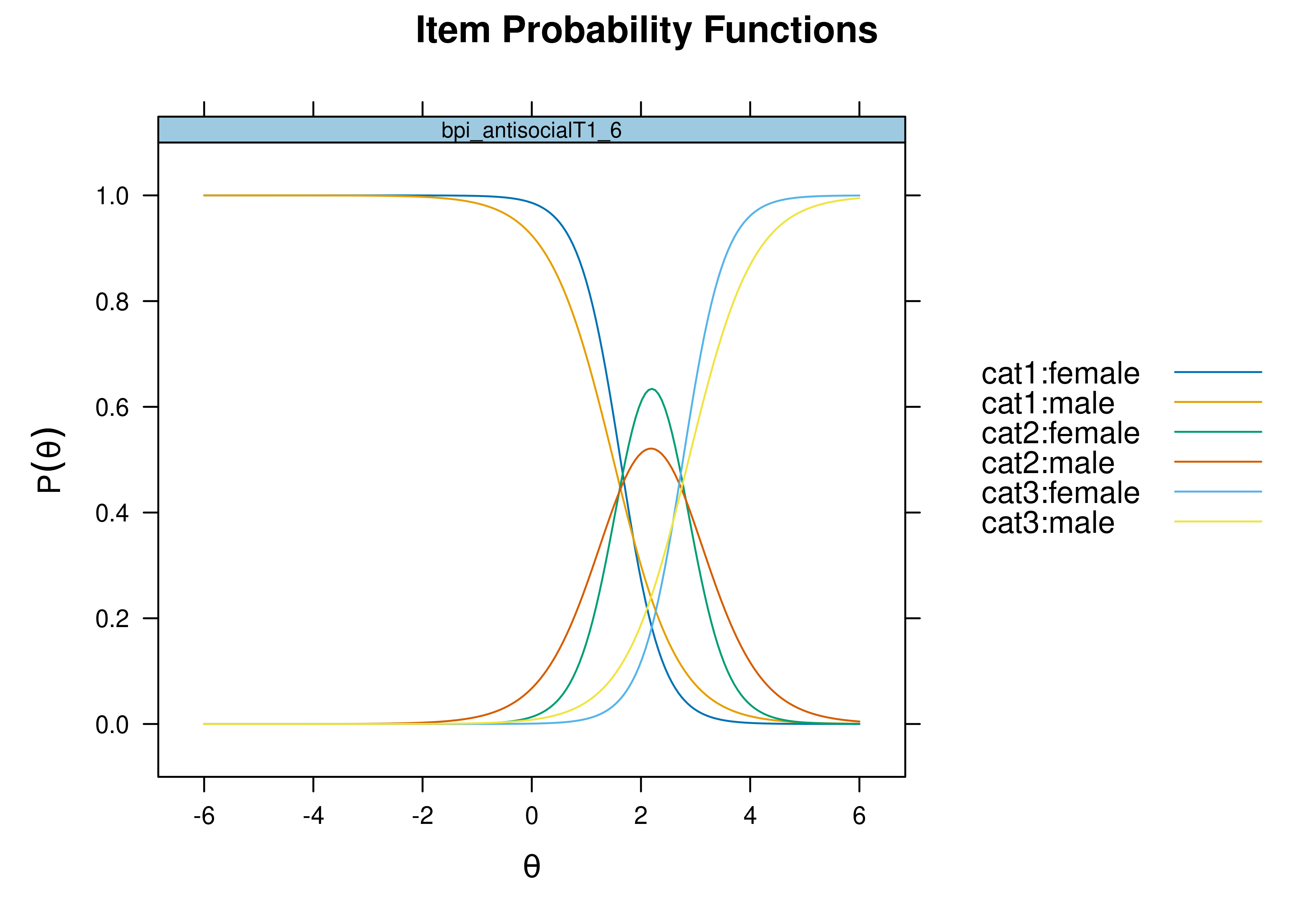
Figure 16.28: Item Probability Functions for Examining Differential Item Functioning in Terms of Discrimination.

Code

difAddItemsDiscrimination

16.9.6.3 Items that differ in severity

Items 1, 2, 3, 4, 5, and 6 showed DIF in difficulty/severity, based on a significant chi-square difference test. The DIF in difficulty/severity is depicted in Figure 16.29

Code

difAddItemsSeverity <- DIF(
  unconstrainedModel,
  c("d1","d2"),
  scheme = "add",
  simplify = TRUE,
  plotdif = TRUE)

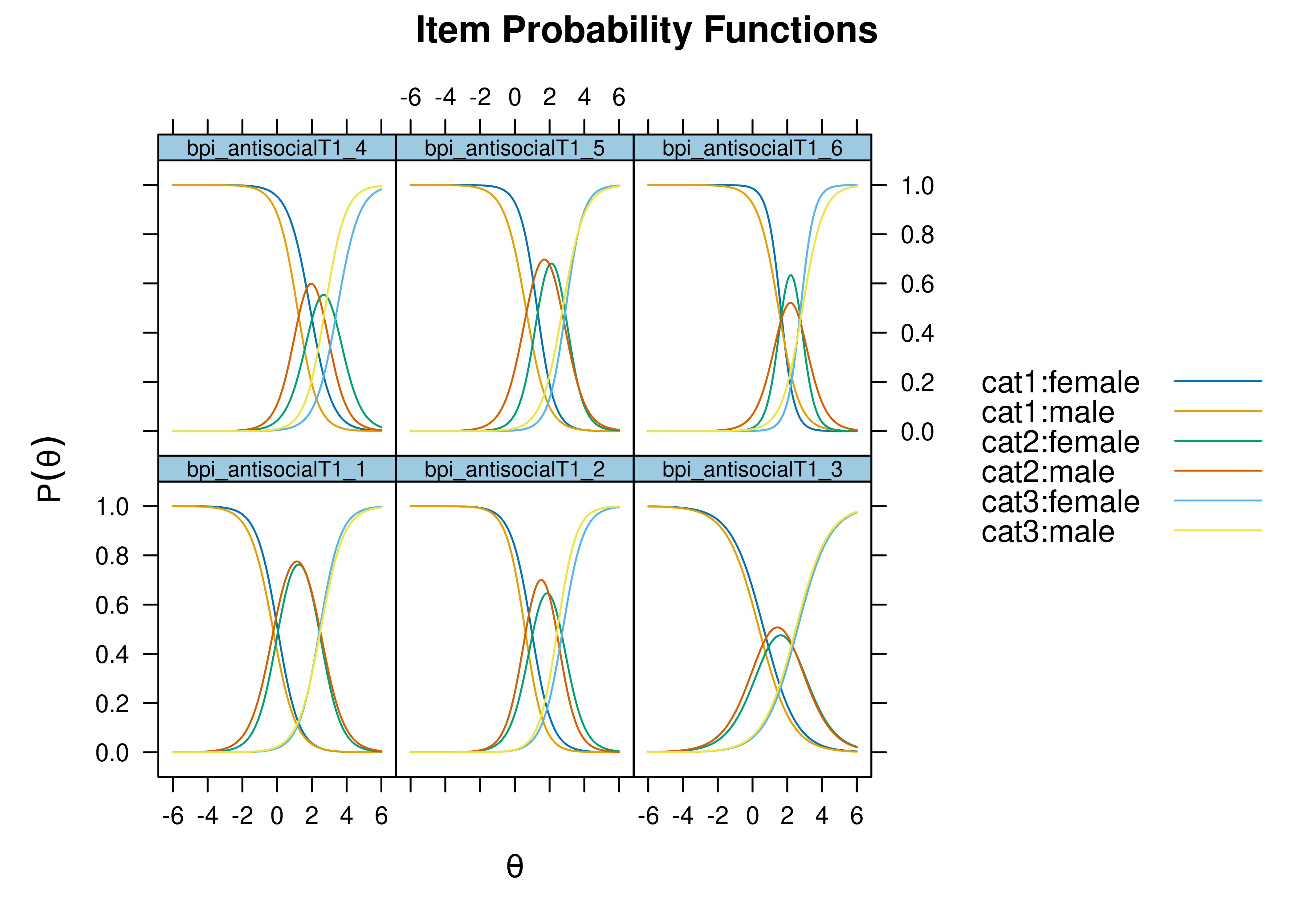
Figure 16.29: Item Probability Functions for Examining Differential Item Functioning in Terms of Severity.

Code

difAddItemsSeverity

16.9.7 Compute effect size of DIF

Effect size measures of DIF were computed based on expected scores (Meade, 2010) using the mirt package (Chalmers, 2020). Some researchers recommend using a simulation-based procedure to examine the impact of DIF on screening accuracy (Gonzalez & Pelham, 2021).

16.9.7.1 Test-level DIF

In addition to consideration of differential test functioning, we can also consider whether the test as a whole (i.e., the collection of items) differs in its functioning by group—called differential test functioning. Differential test functioning is depicted in Figure 16.30. Estimates of differential test functioning are in Table ??.

Code

empirical_ES(
  unconstrainedModel,
  DIF = FALSE)

In general, the measure showed greater difficulty for females than for males. That is, at a given construct level, males were more likely than females to endorse the items. Otherwise said, it takes a higher construct level for females to obtain the same score on the measure as males.

Code

empirical_ES(
  unconstrainedModel,
  DIF = FALSE,
  plot = TRUE)

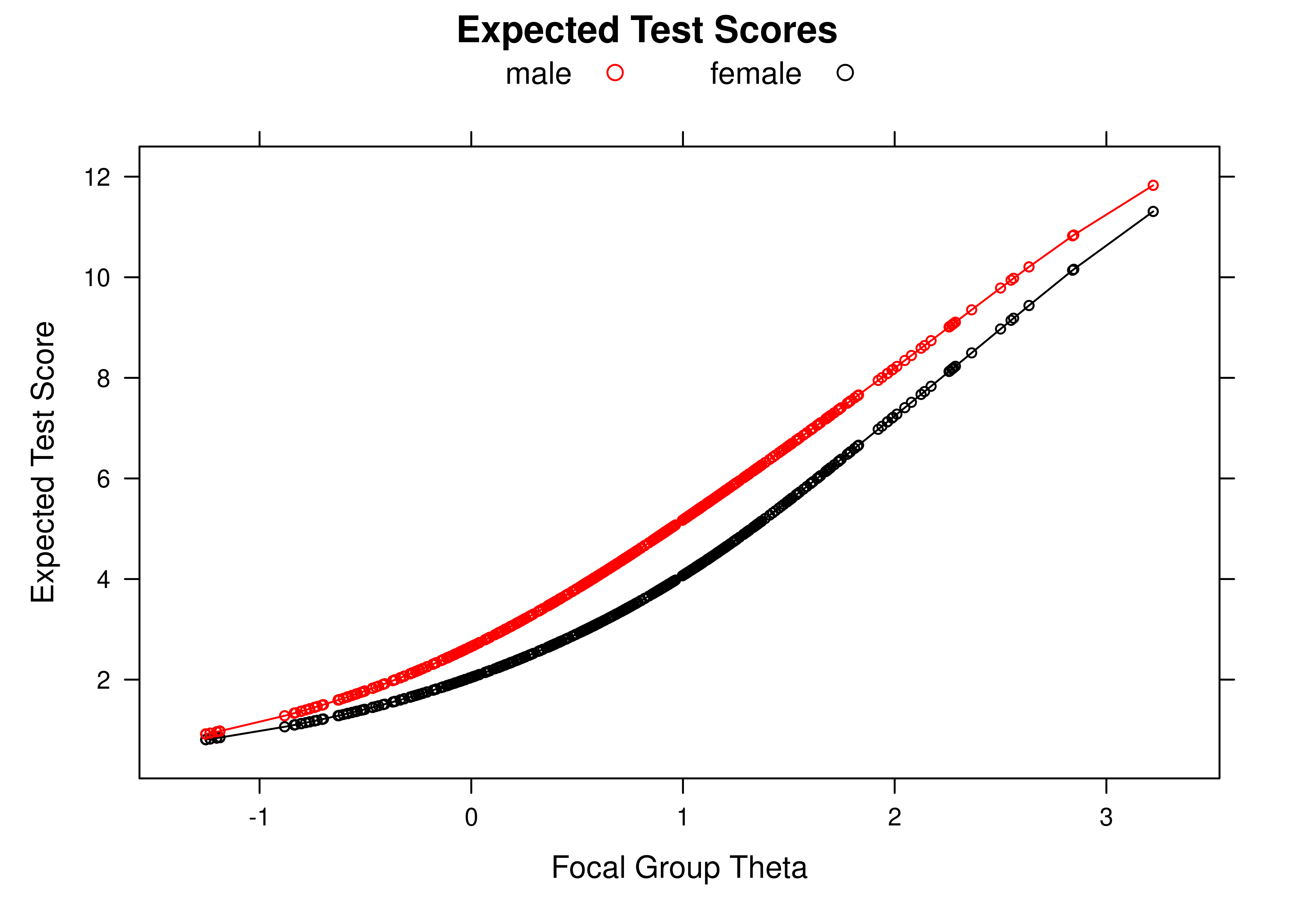
Figure 16.30: Differential Test Functioning by Sex.

16.9.7.2 Item-level DIF

Differential item functioning is depicted in Figure 16.31. Estimates of differential item functioning are in Table ??.

Code

empirical_ES(
  unconstrainedModel,
  DIF = TRUE) %>% 
  round(., 2)

The measure-level differences in functioning appear to be largely driven by greater difficulty of items 4 and 5 for females than males. That is, at a given construct level, males were more likely than females to endorse items 4 and 5, in particular. Otherwise said, it takes a higher construct level for females than males to endorse items 4 and 5.

Code

empirical_ES(
  unconstrainedModel,
  DIF = TRUE,
  plot = TRUE)

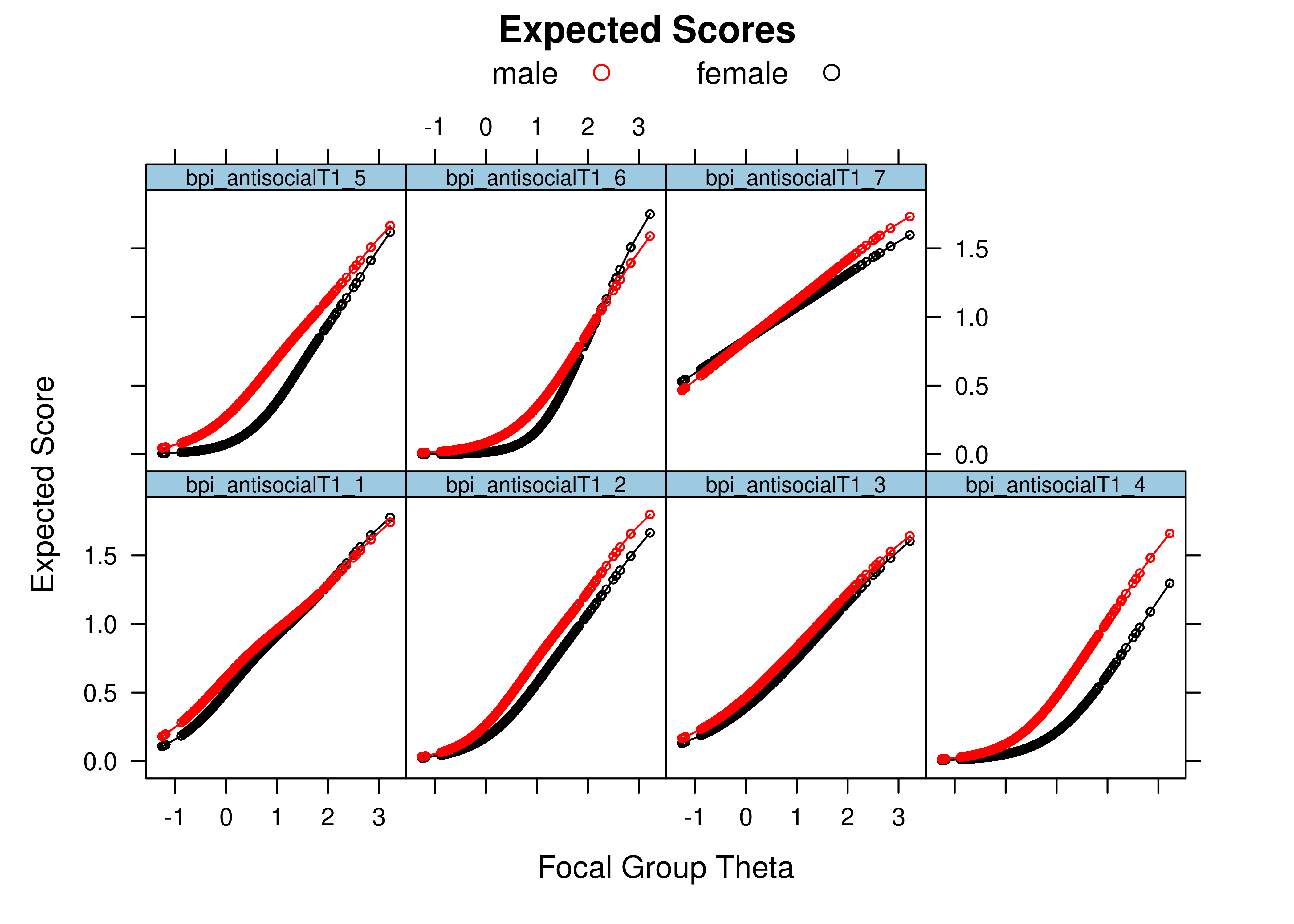
Figure 16.31: Differential Item Functioning by Sex.

16.9.8 Item plots

Plots of item response category characteristic curves by sex are in Figures 16.32–16.38 below.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_1",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

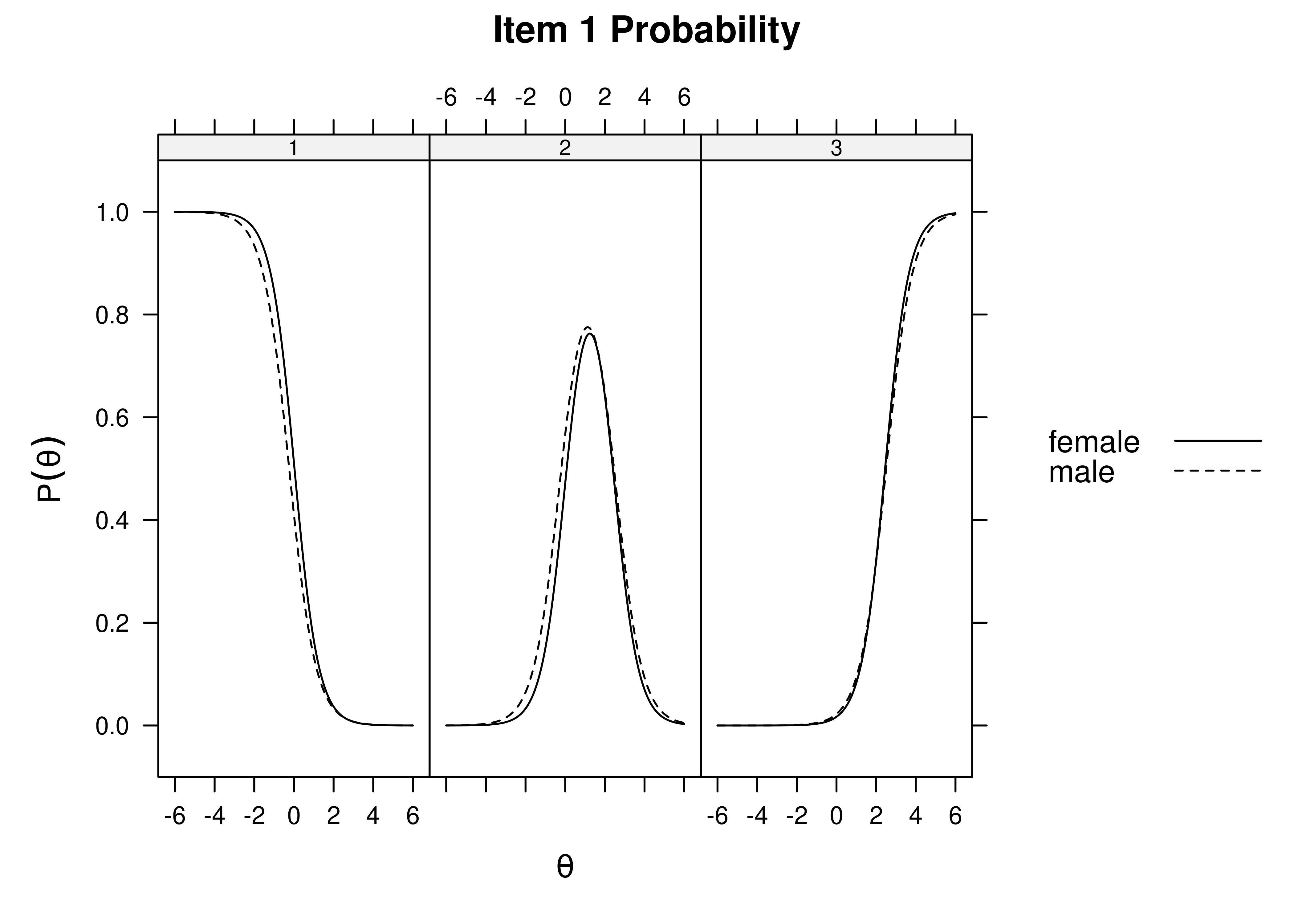
Figure 16.32: Item Response Category Characteristic Curves by Sex: Item 1.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_2",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

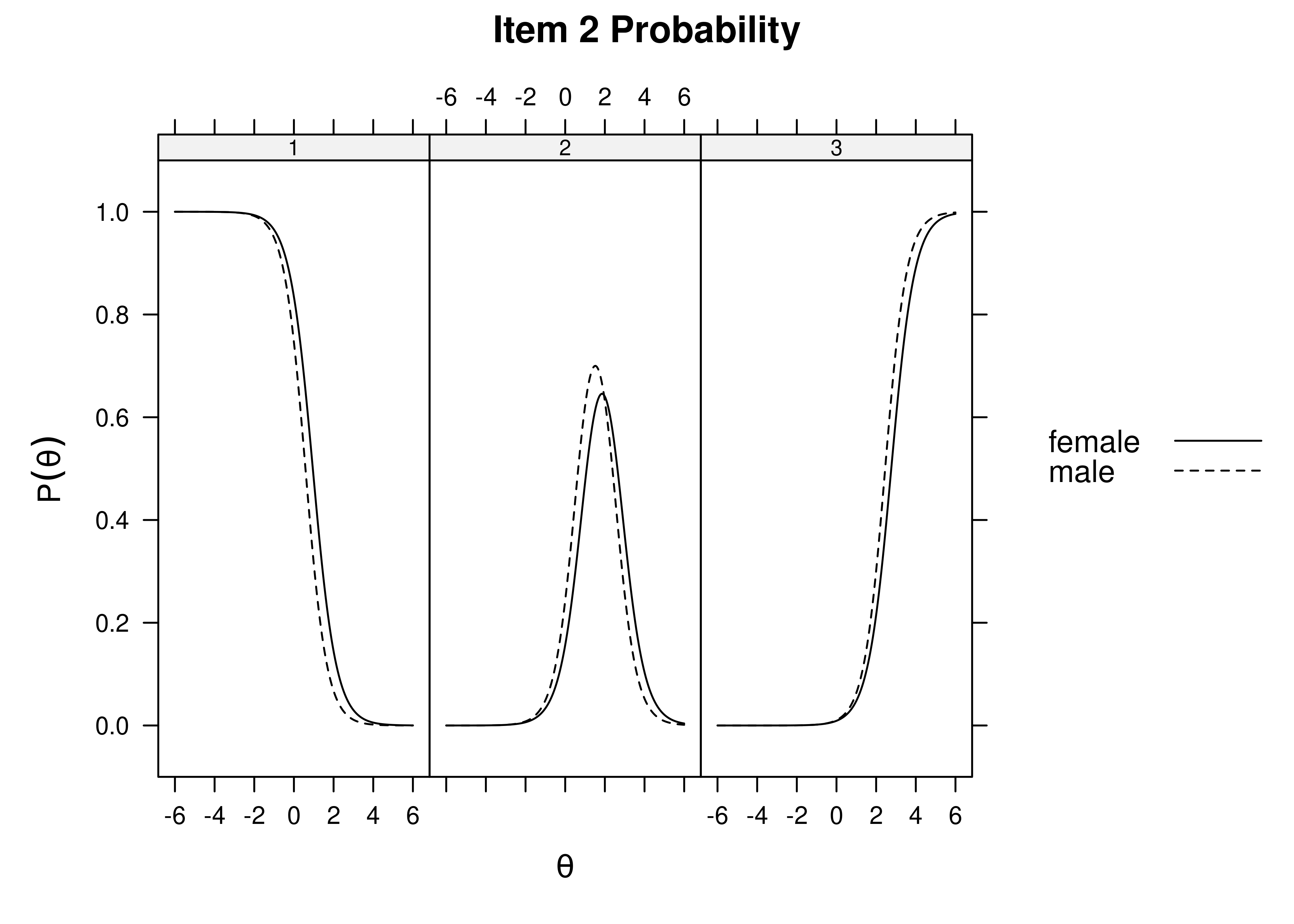
Figure 16.33: Item Response Category Characteristic Curves by Sex: Item 2.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_3",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

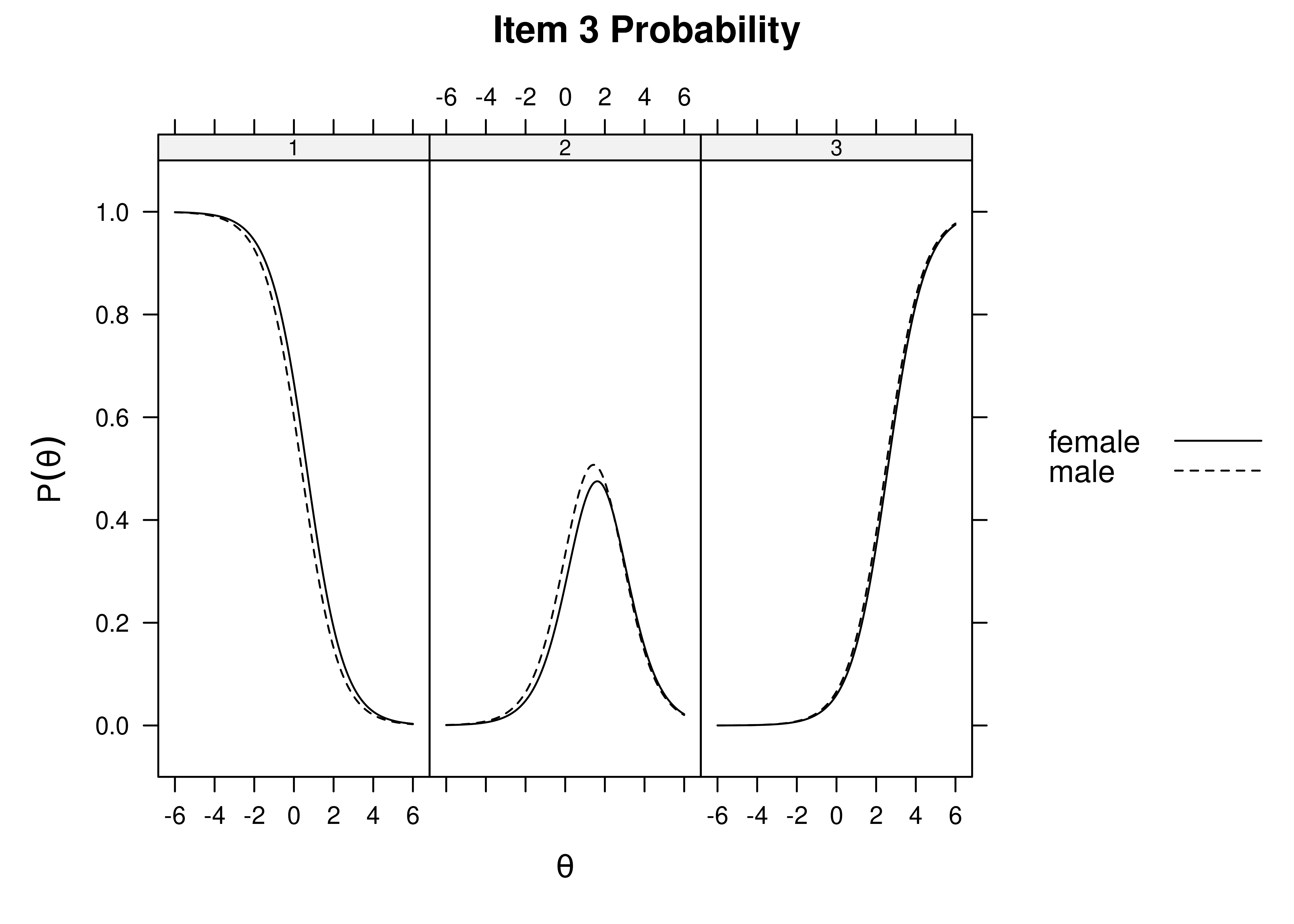
Figure 16.34: Item Response Category Characteristic Curves by Sex: Item 3.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_4",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

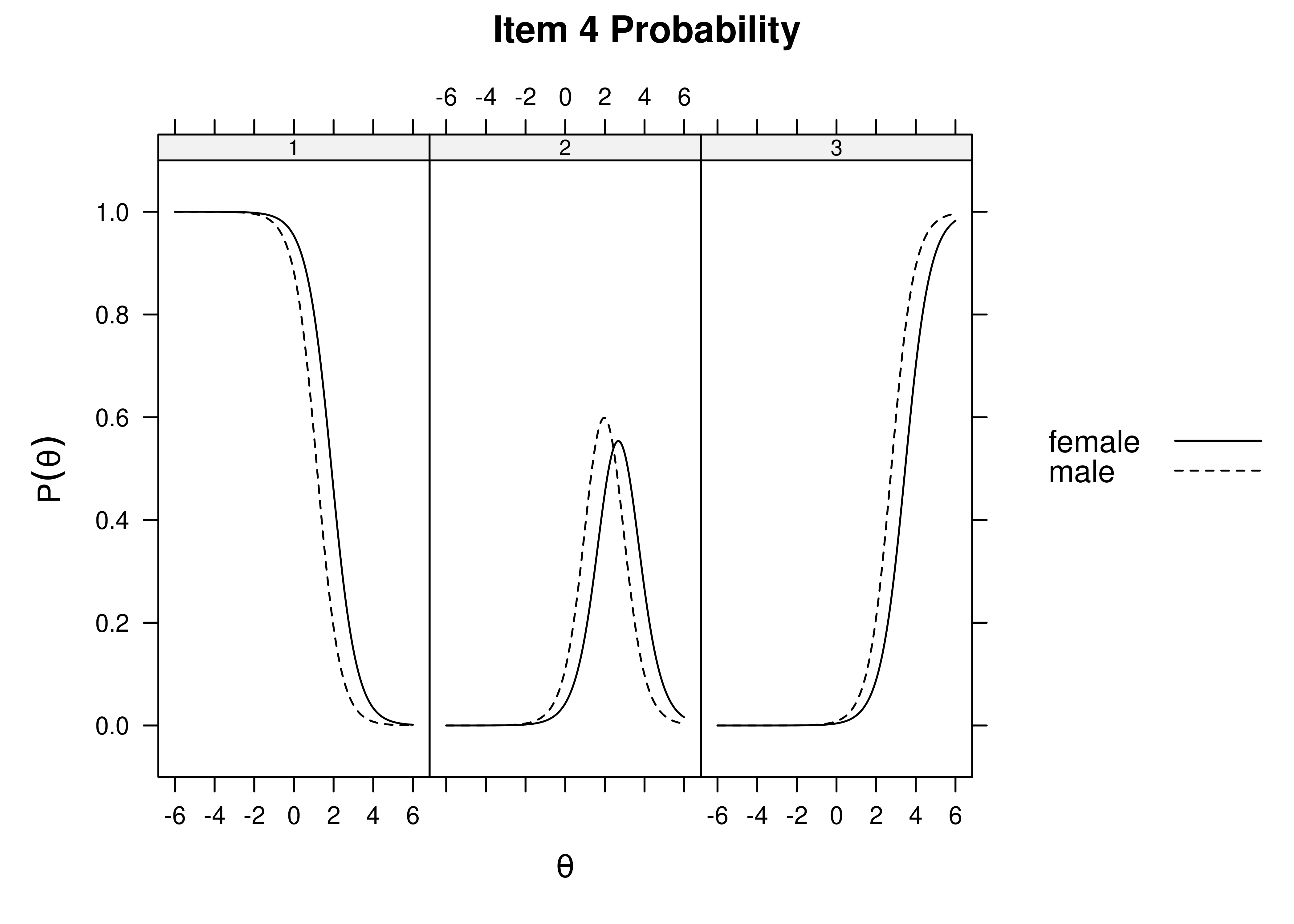
Figure 16.35: Item Response Category Characteristic Curves by Sex: Item 4.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_5",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

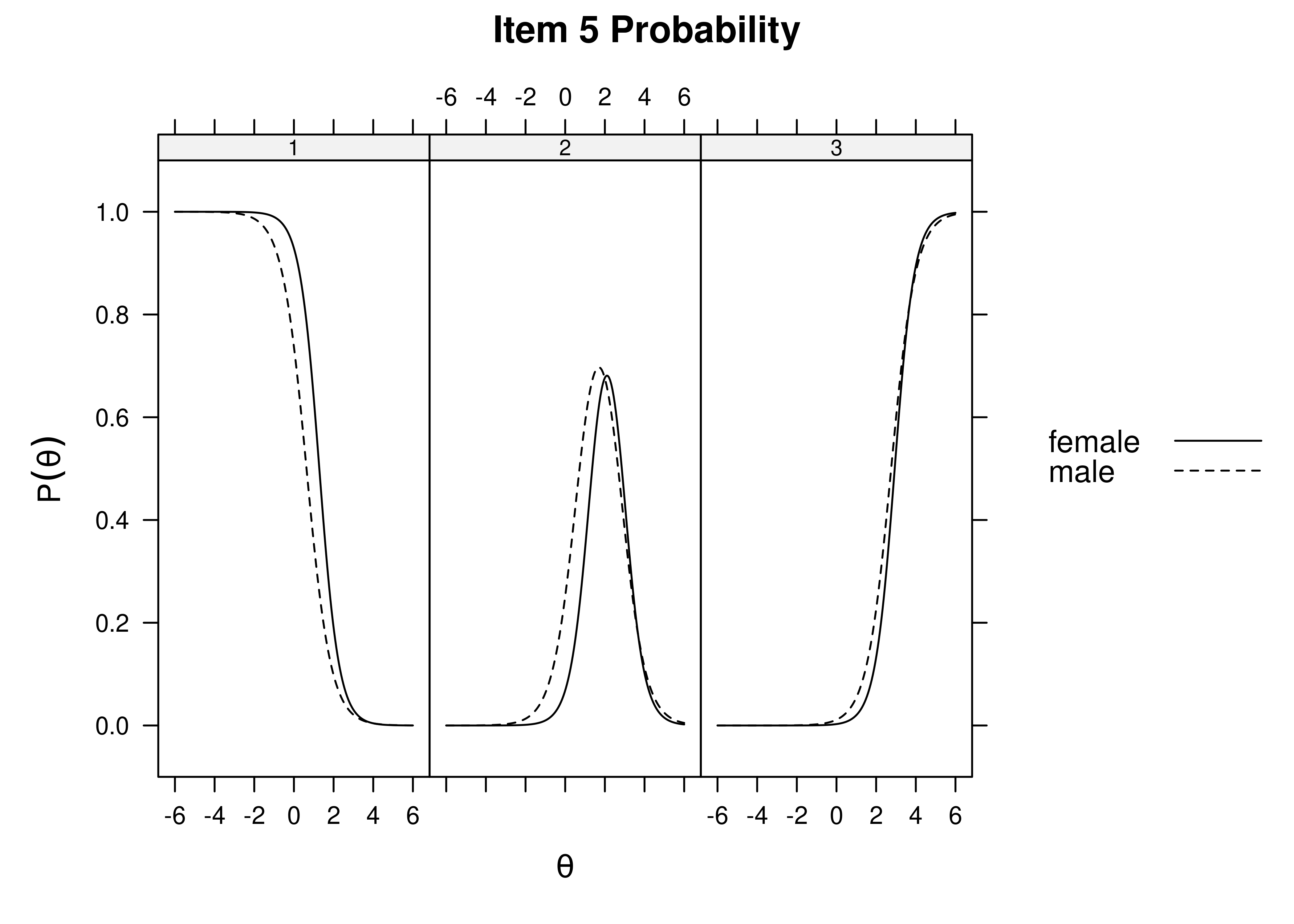
Figure 16.36: Item Response Category Characteristic Curves by Sex: Item 5.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_6",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

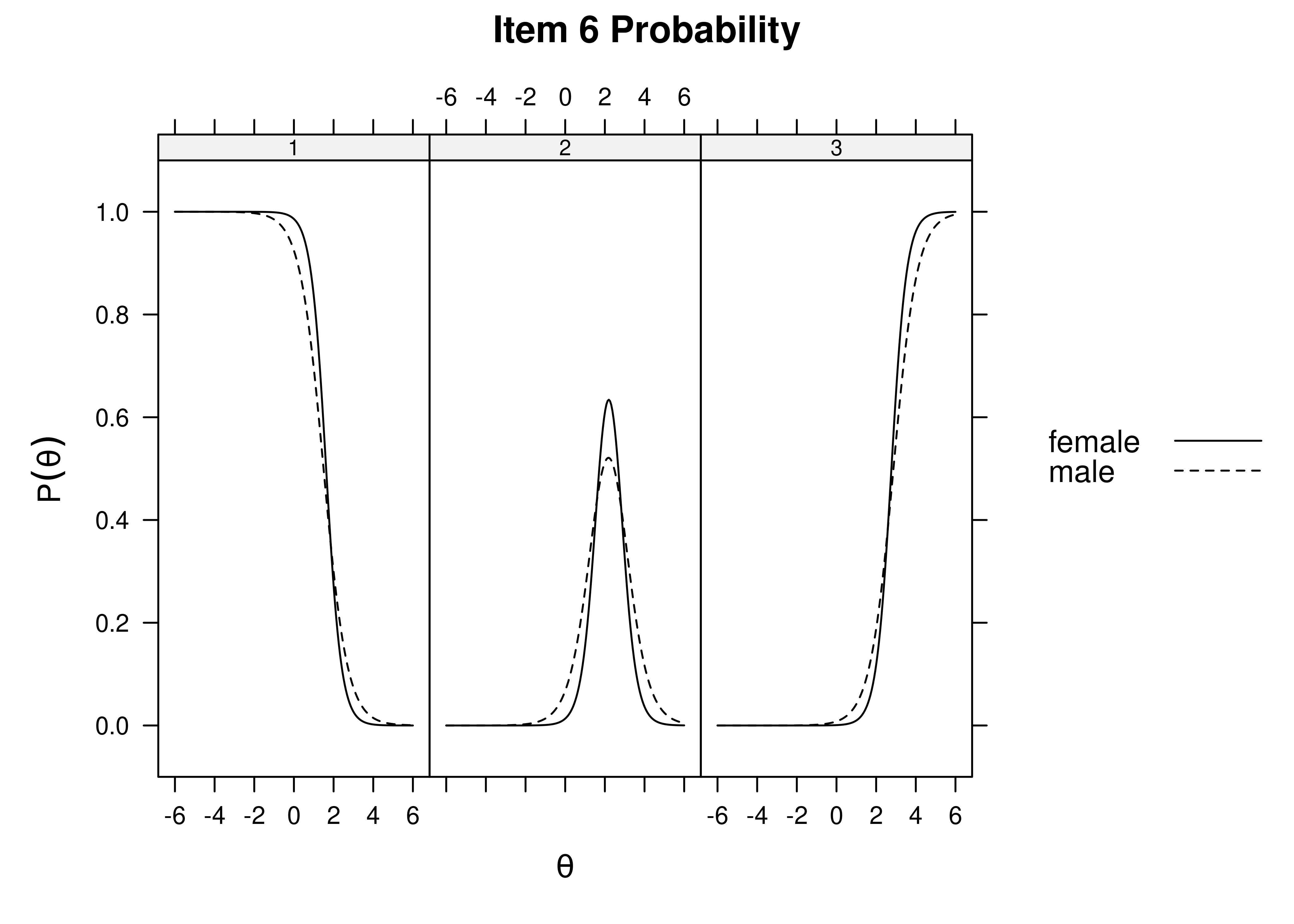
Figure 16.37: Item Response Category Characteristic Curves by Sex: Item 6.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_7",
  type = "trace",
  par.settings = standard.theme("pdf", color = FALSE))

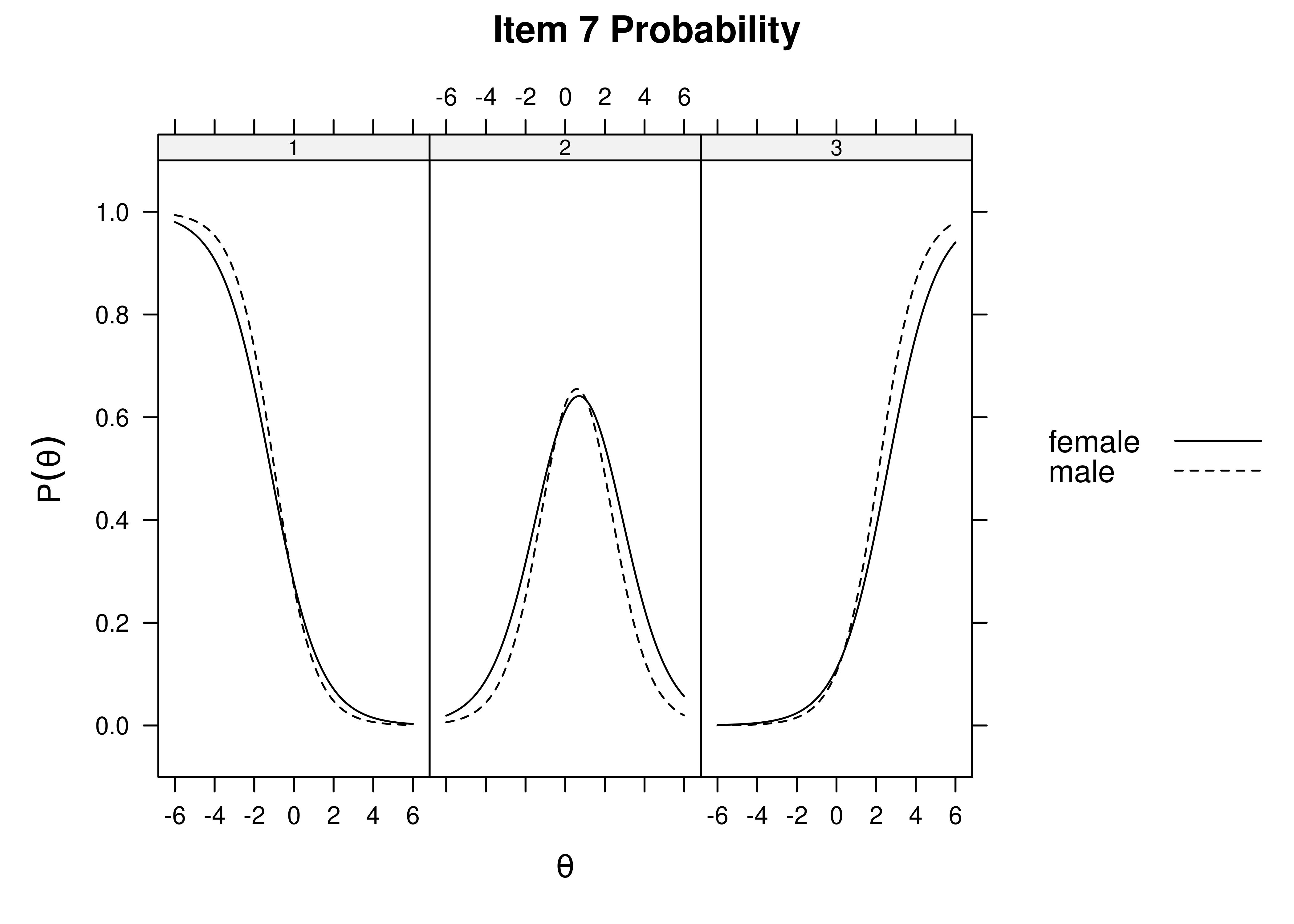
Figure 16.38: Item Response Category Characteristic Curves by Sex: Item 7.

Plots of item information functions by sex are in Figures 16.39–16.45 below. Items 1, 5, and 6 showed greater information for females than for males. Items 2, 4, and 7 showed greater information for females than for males.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_1",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

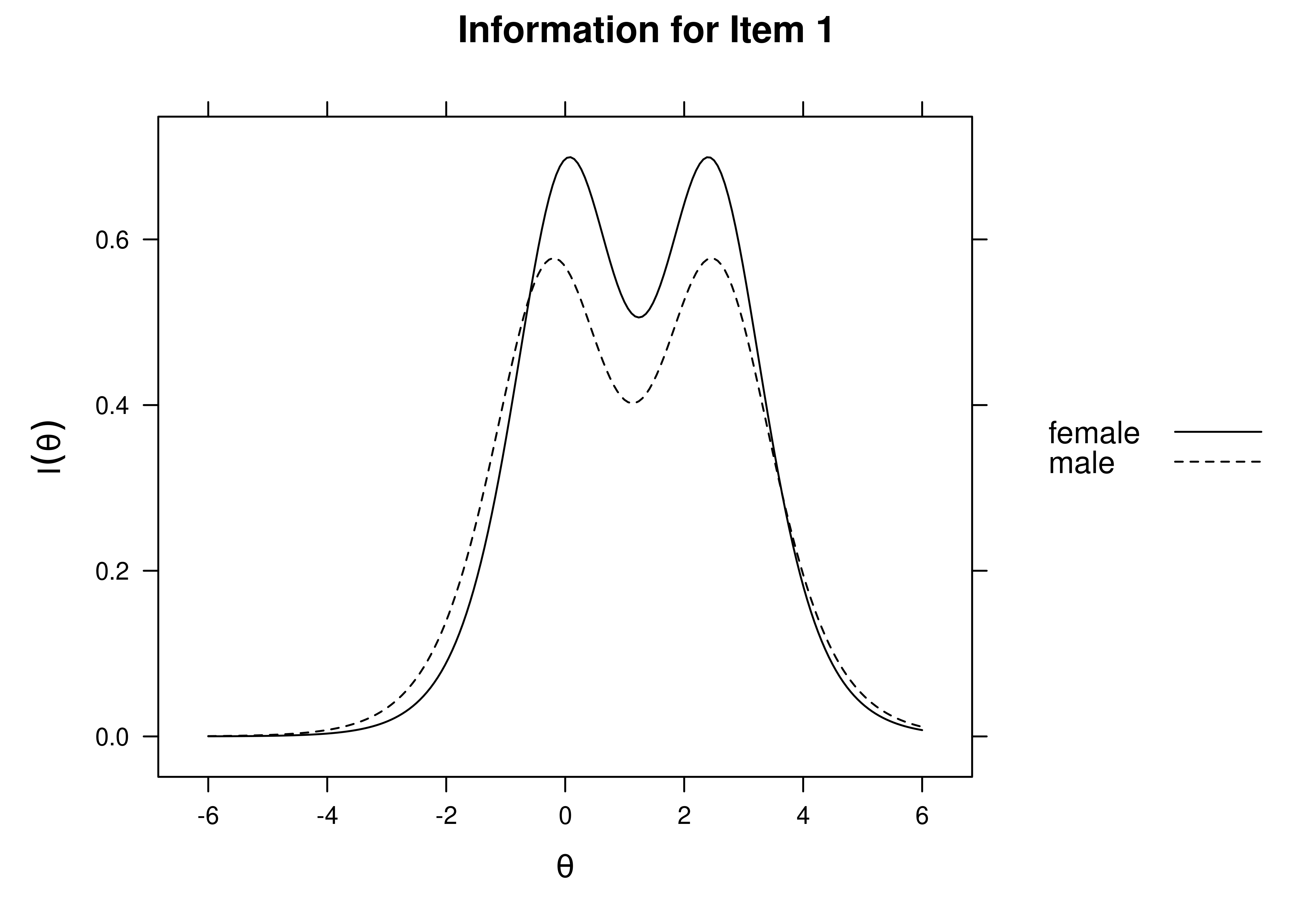
Figure 16.39: Item Information Curves by Sex: Item 1.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_2",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

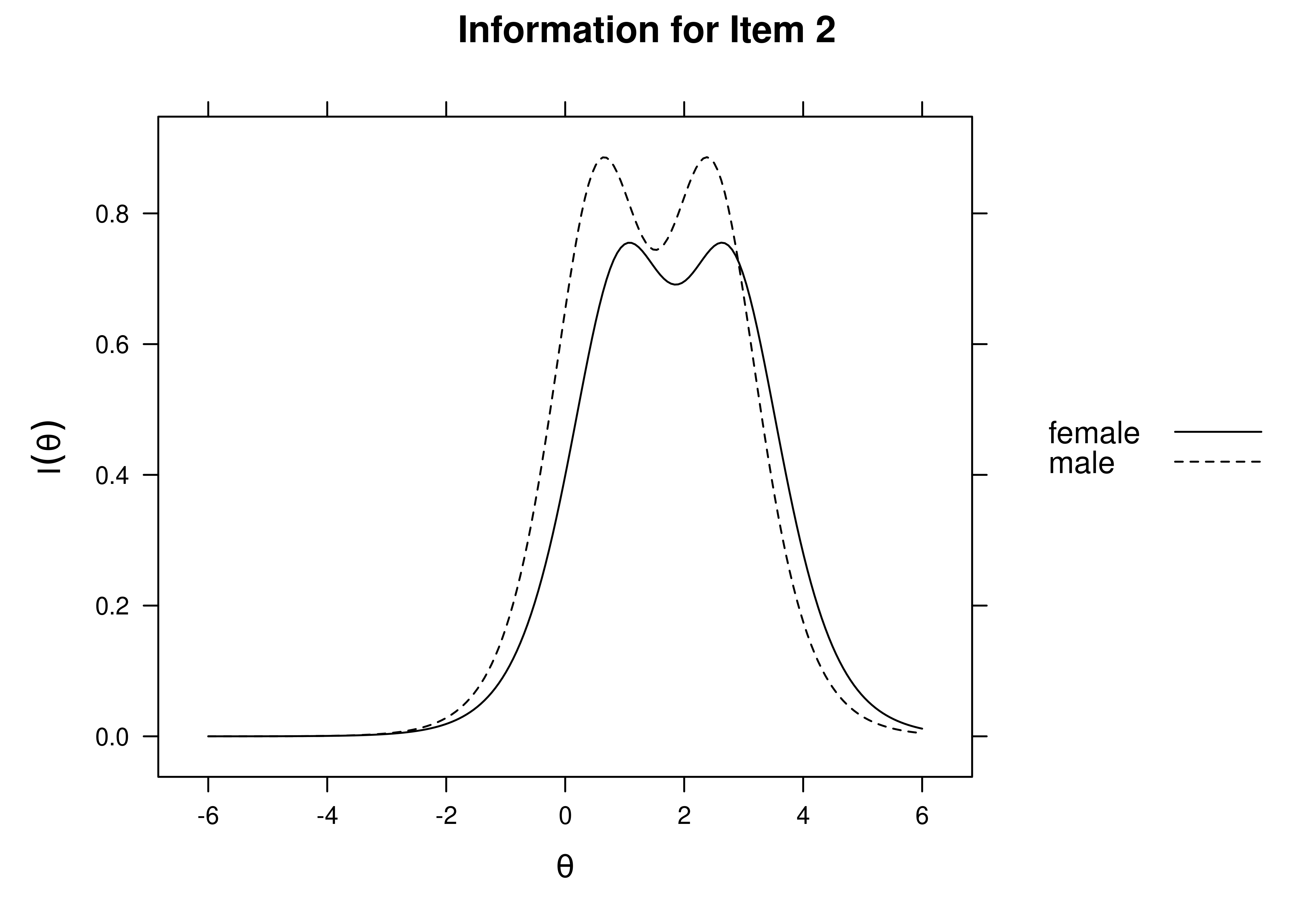
Figure 16.40: Item Information Curves by Sex: Item 2.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_3",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

Figure 16.41: Item Information Curves by Sex: Item 3.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_4",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

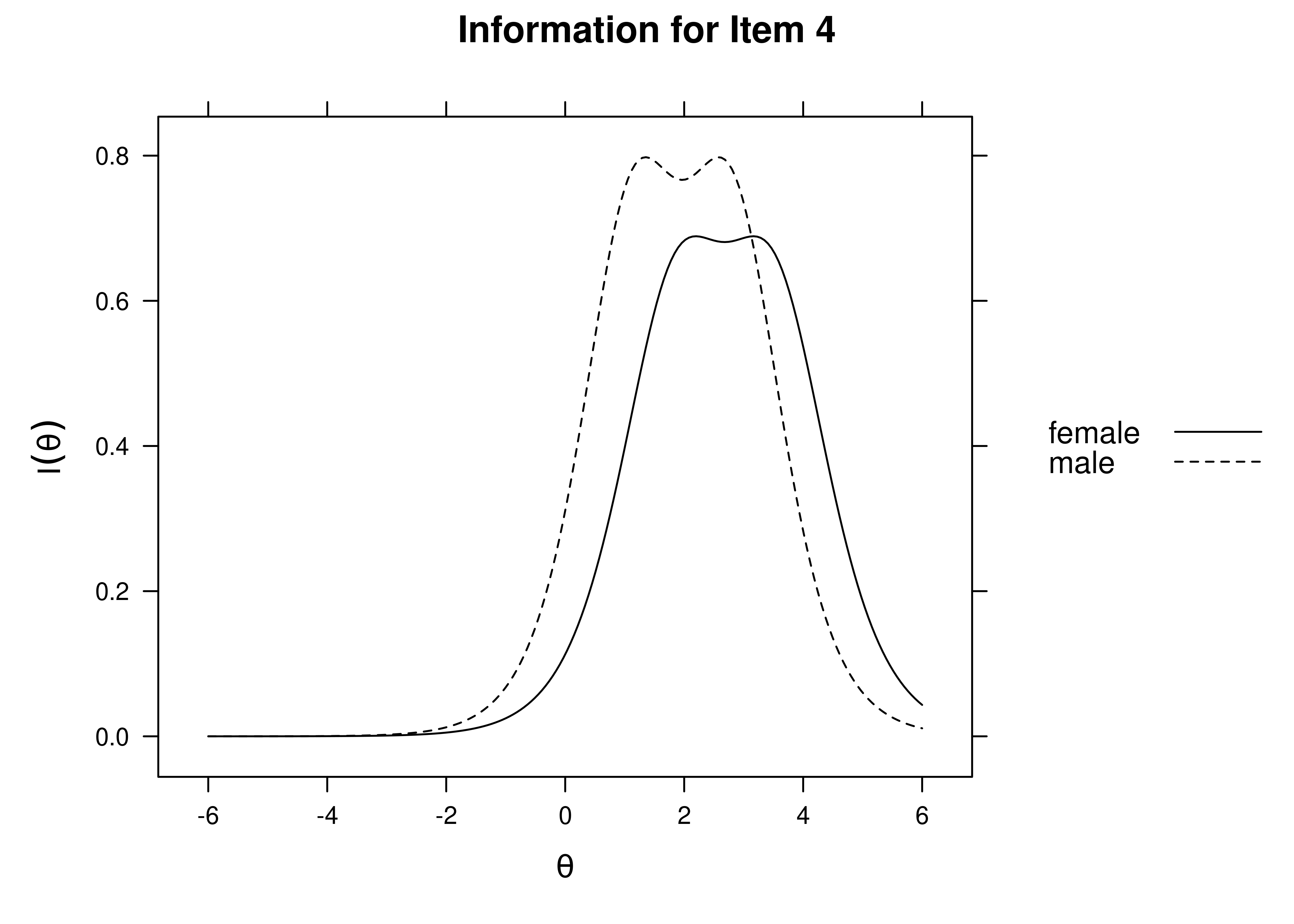
Figure 16.42: Item Information Curves by Sex: Item 4.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_5",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

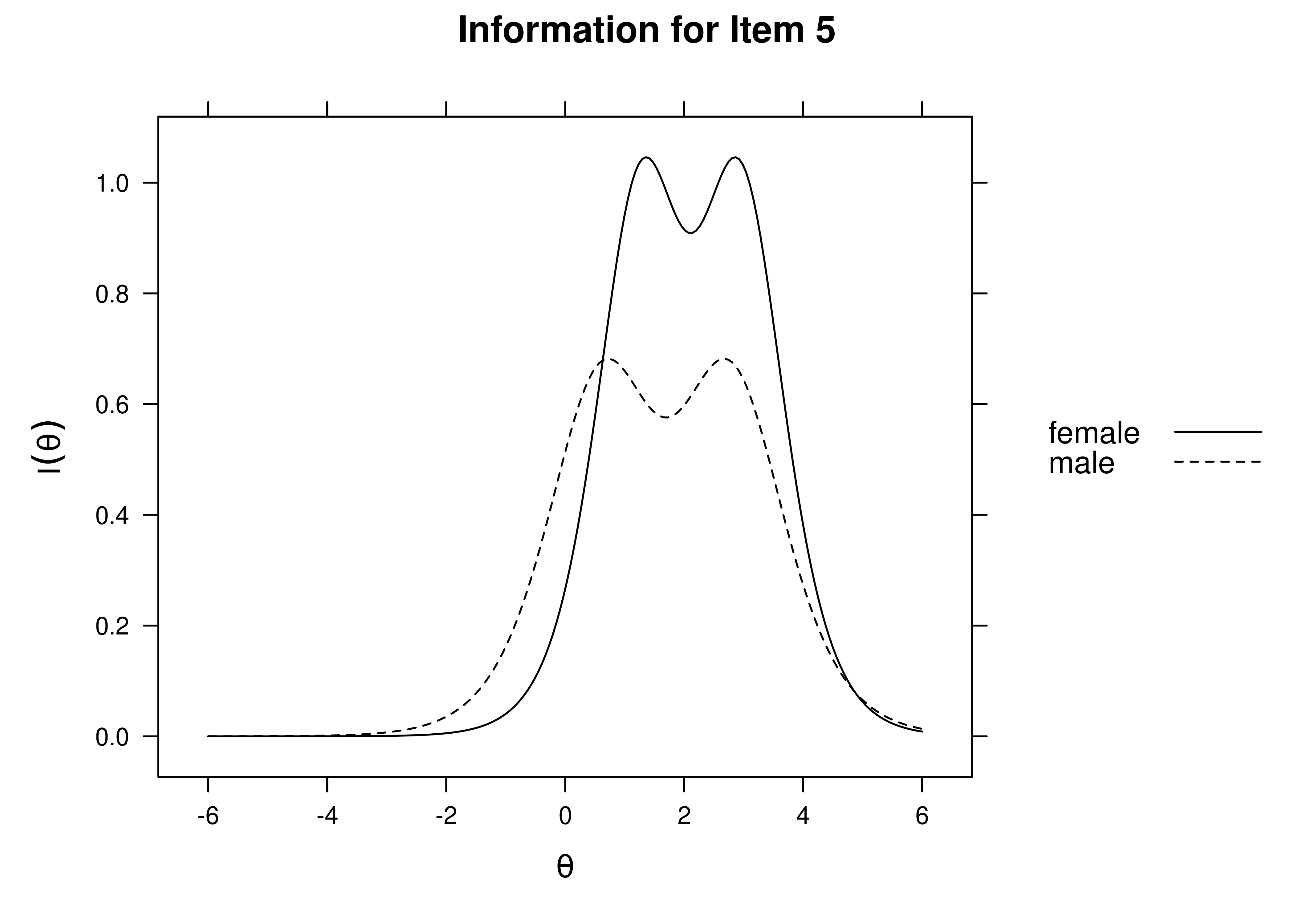
Figure 16.43: Item Information Curves by Sex: Item 5.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_6",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

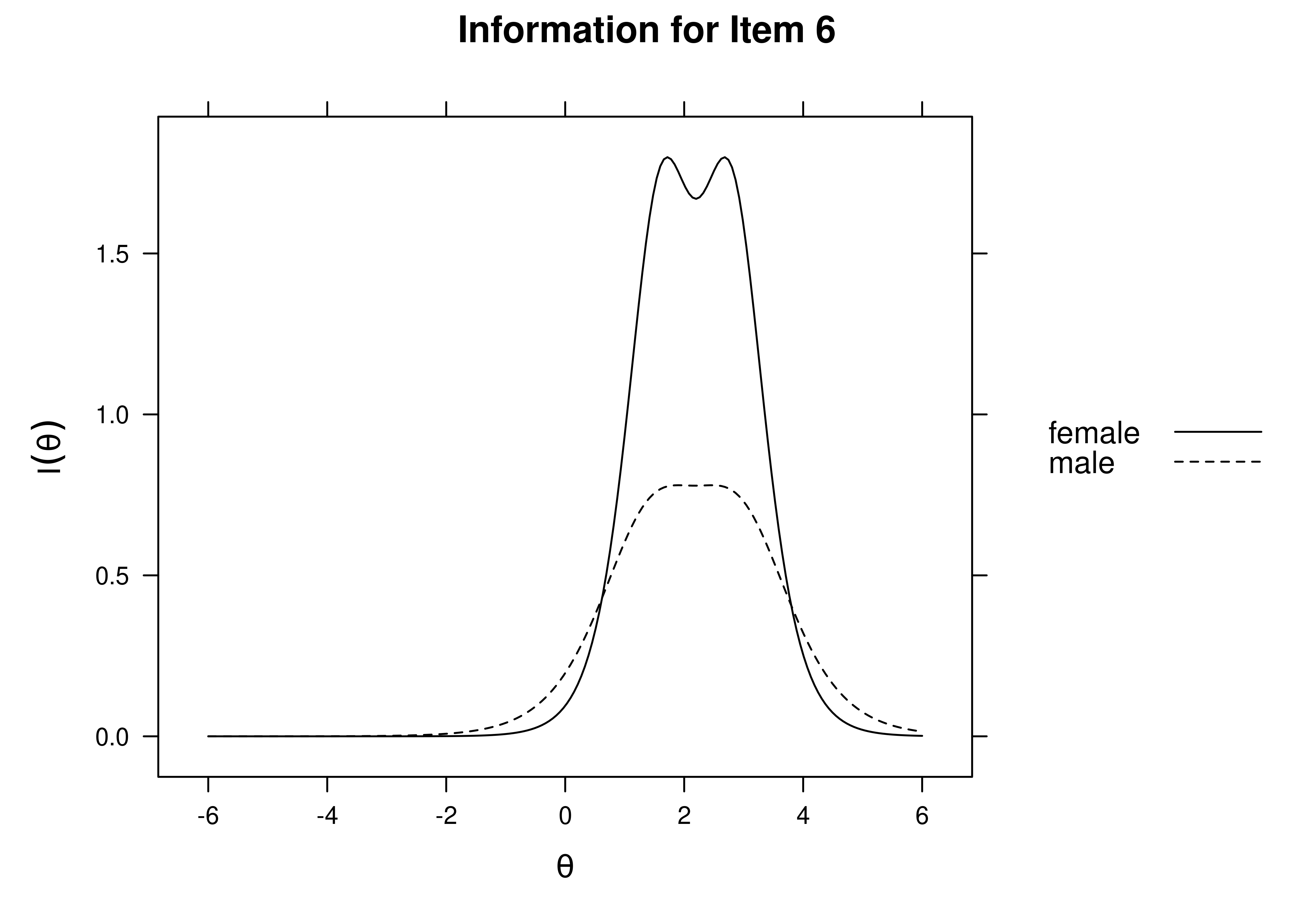
Figure 16.44: Item Information Curves by Sex: Item 6.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_7",
  type = "info",
  par.settings = standard.theme("pdf", color = FALSE))

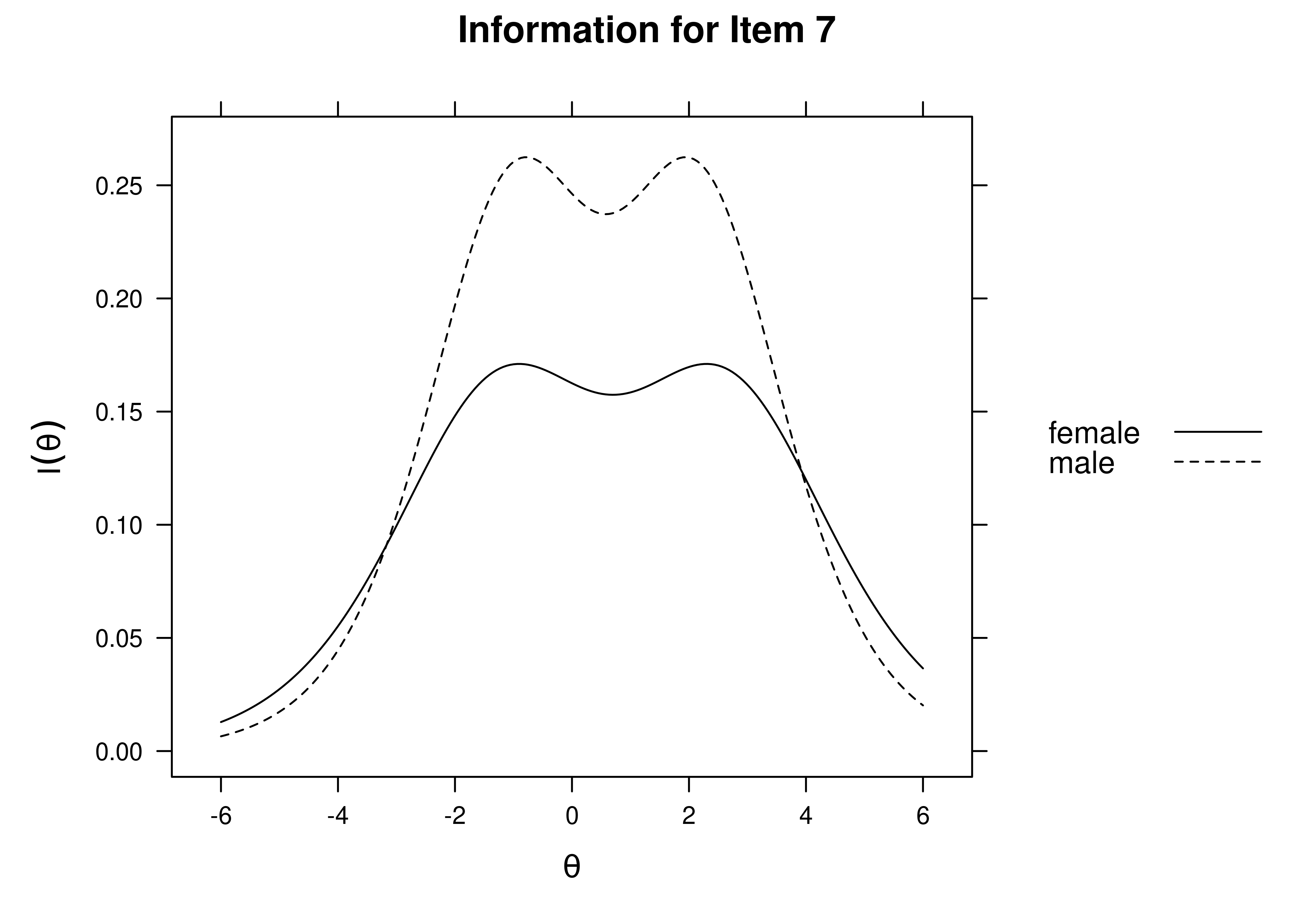
Figure 16.45: Item Information Curves by Sex: Item 7.

Plots of expected item scores by sex are are in Figures 16.46–16.52 below.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_1",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

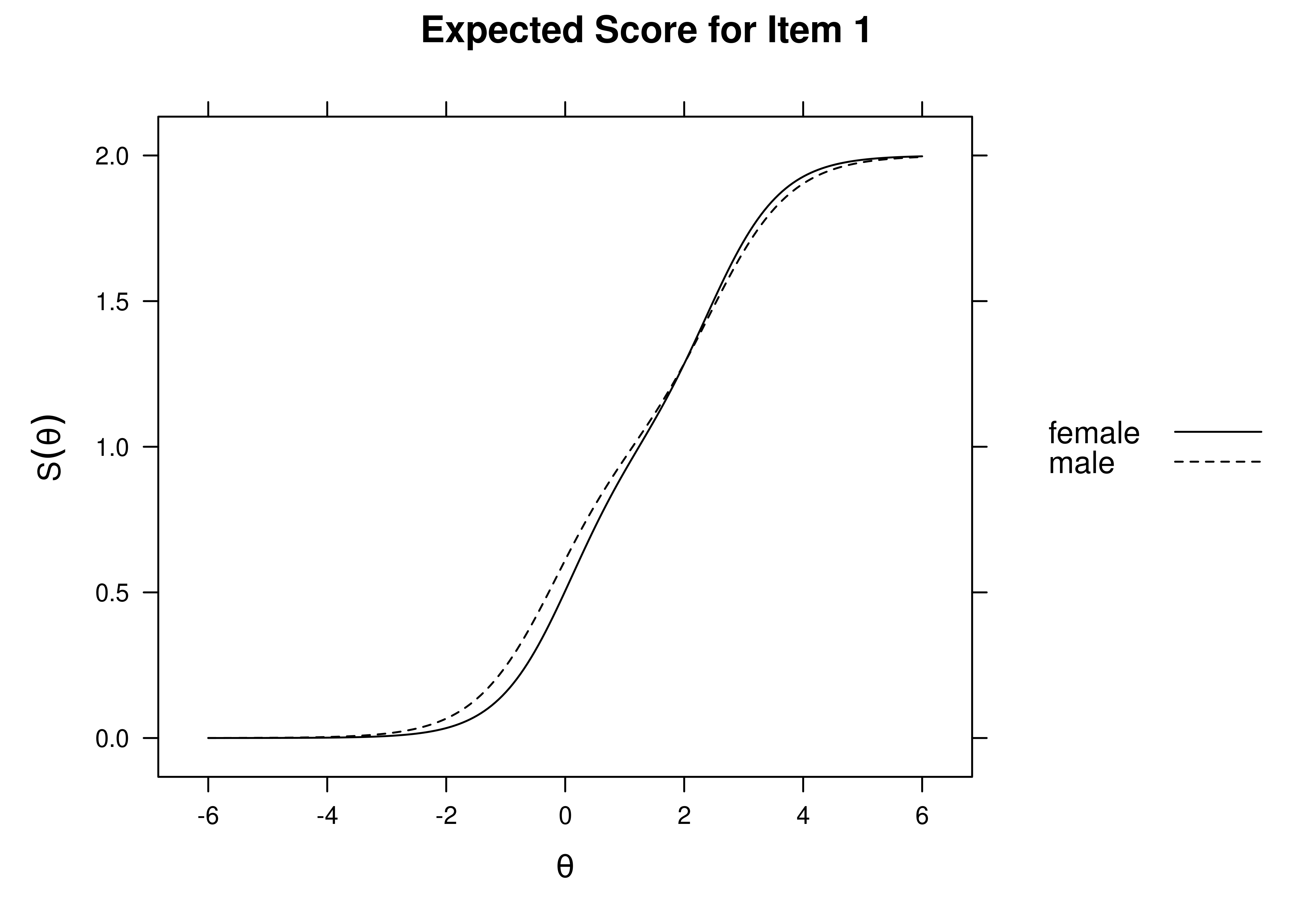
Figure 16.46: Expected Item Score by Sex: Item 1.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_2",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

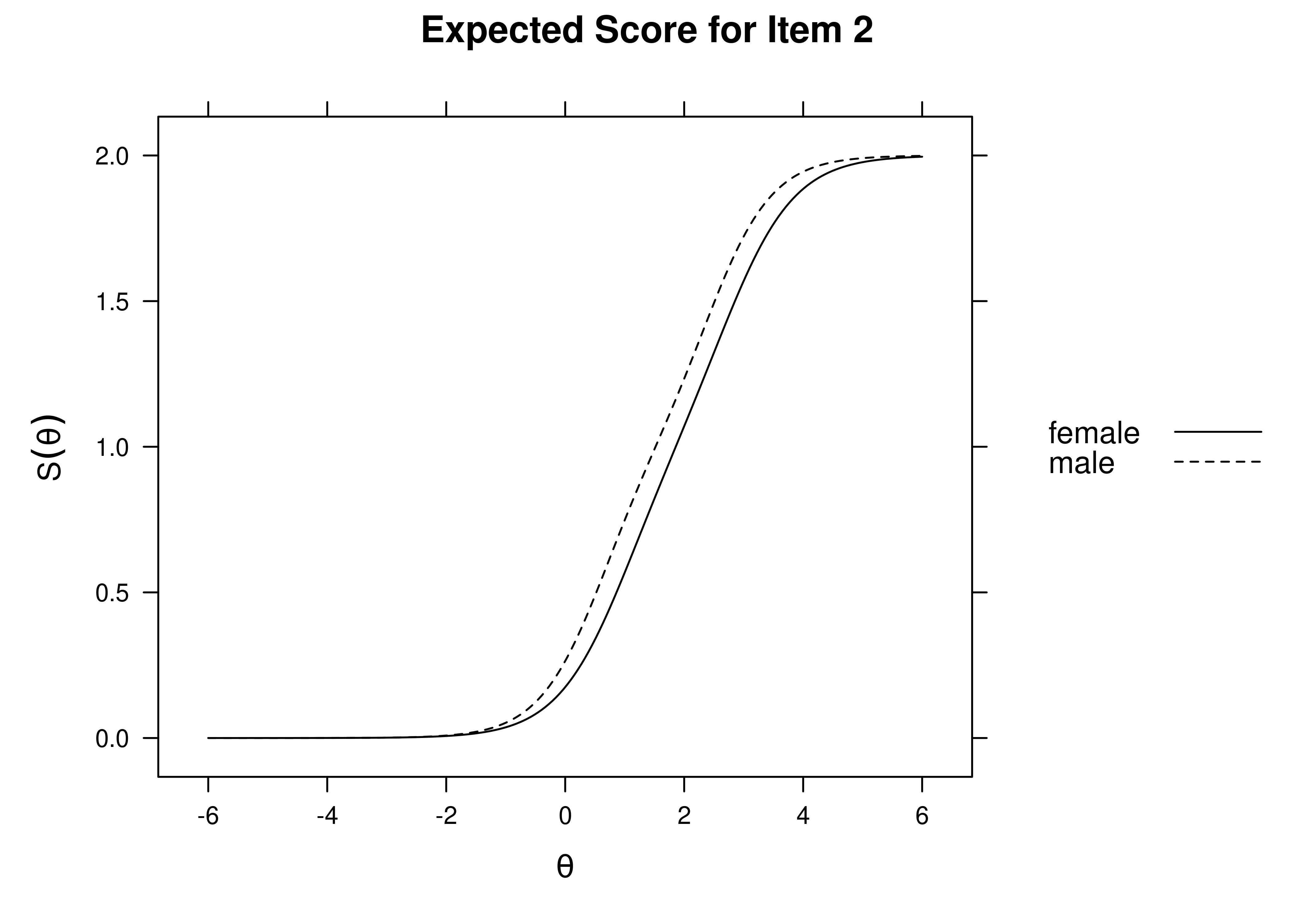
Figure 16.47: Expected Item Score by Sex: Item 2.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_3",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

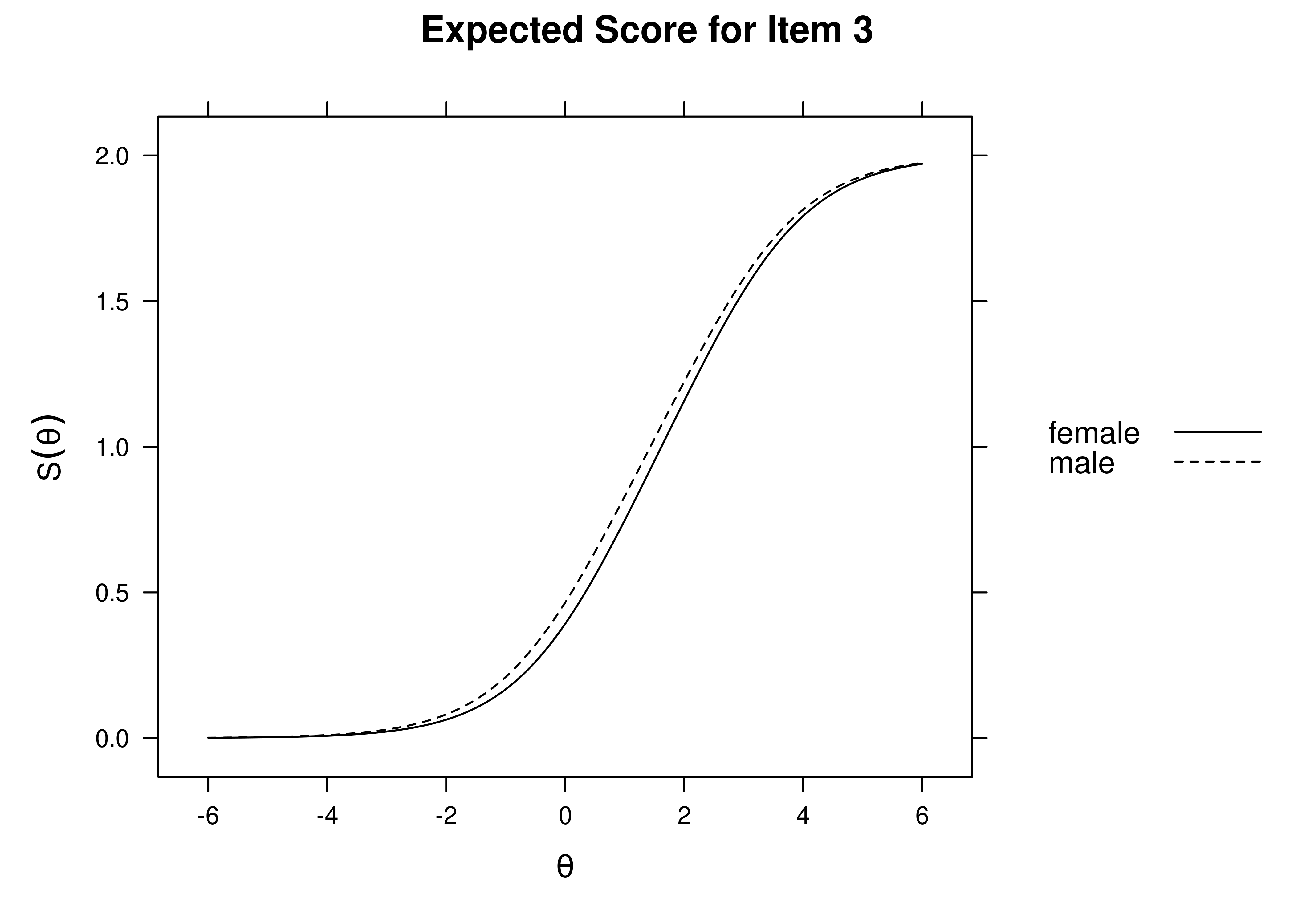
Figure 16.48: Expected Item Score by Sex: Item 3.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_4",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

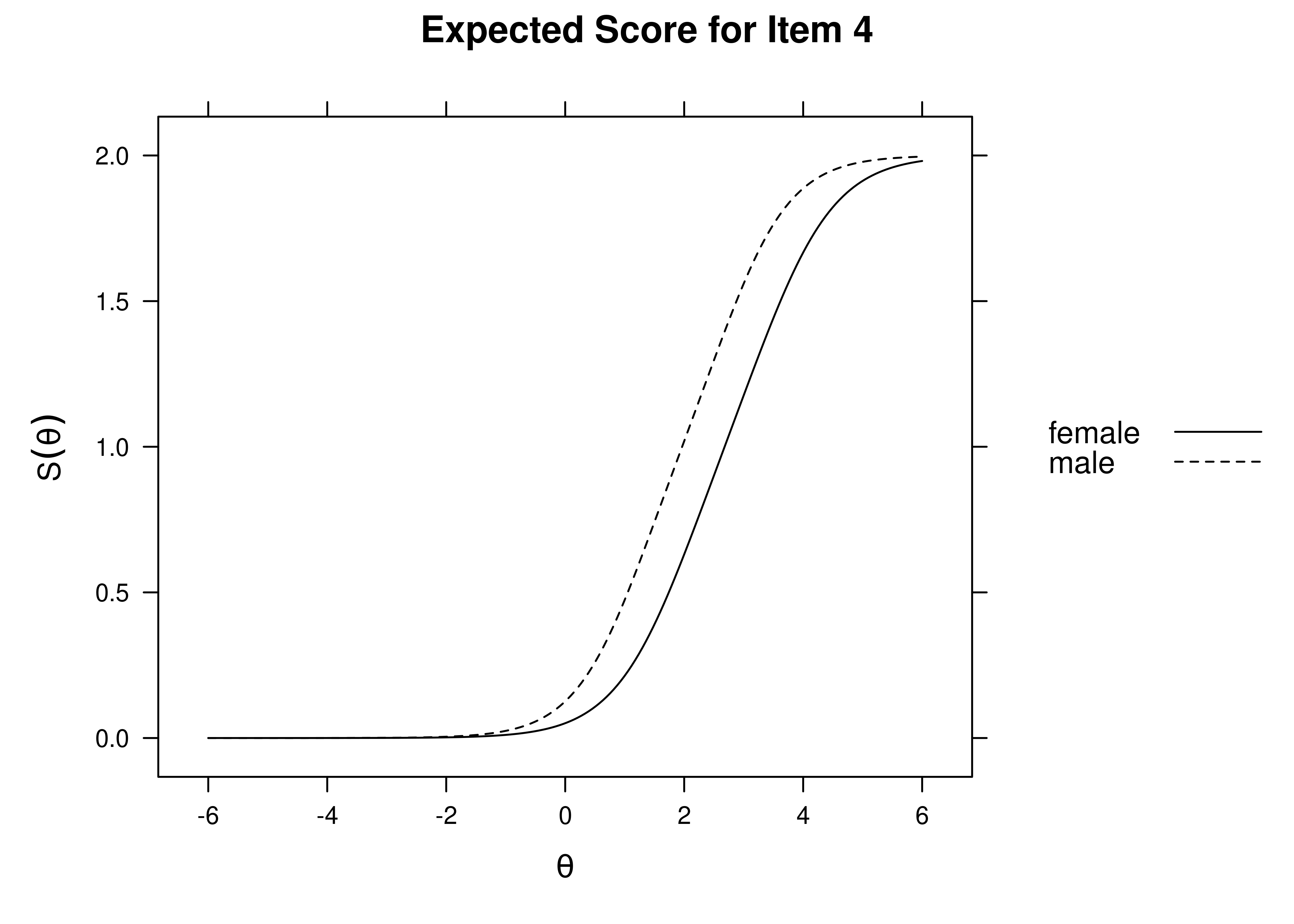
Figure 16.49: Expected Item Score by Sex: Item 4.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_5",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

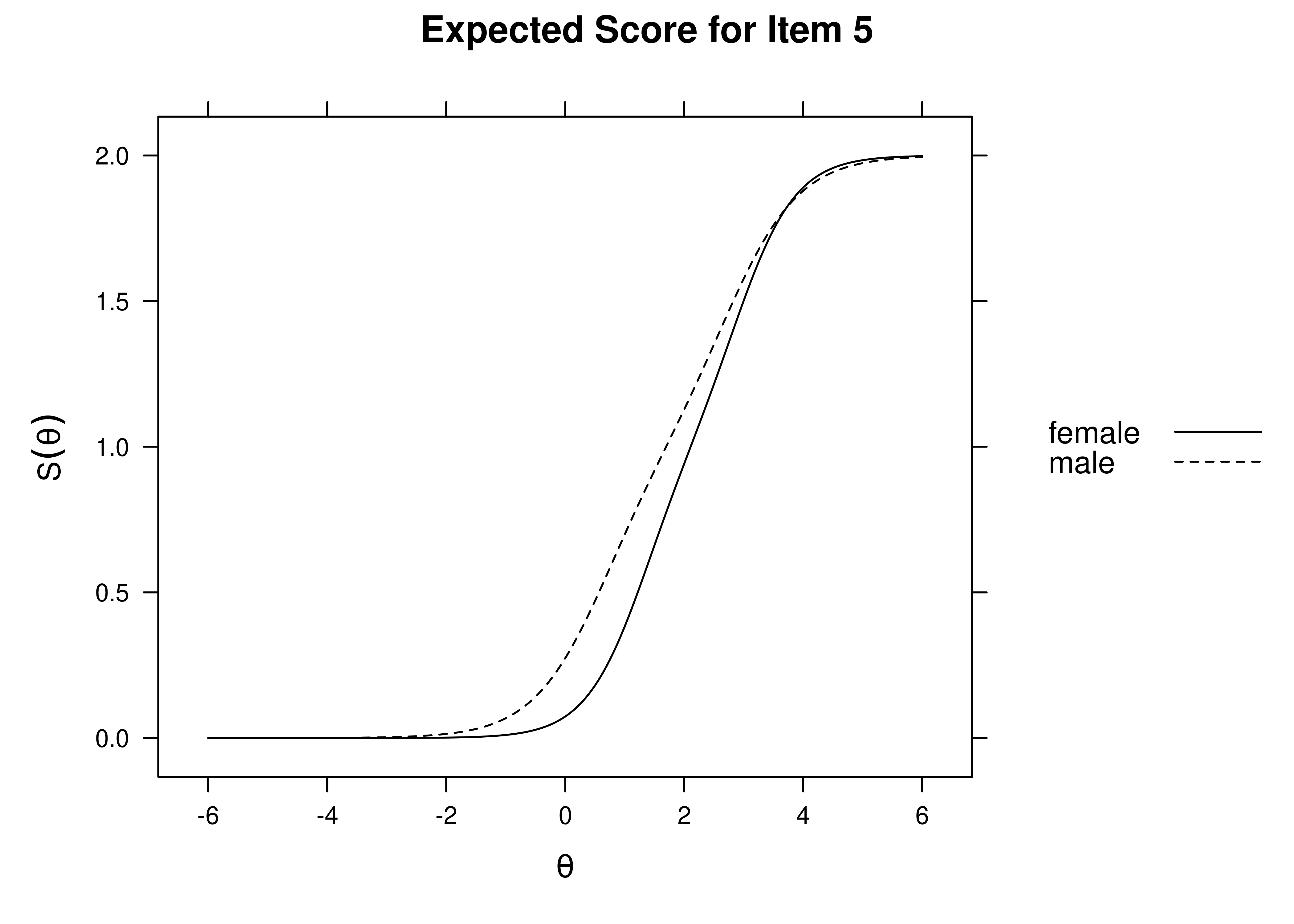
Figure 16.50: Expected Item Score by Sex: Item 5.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_6",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

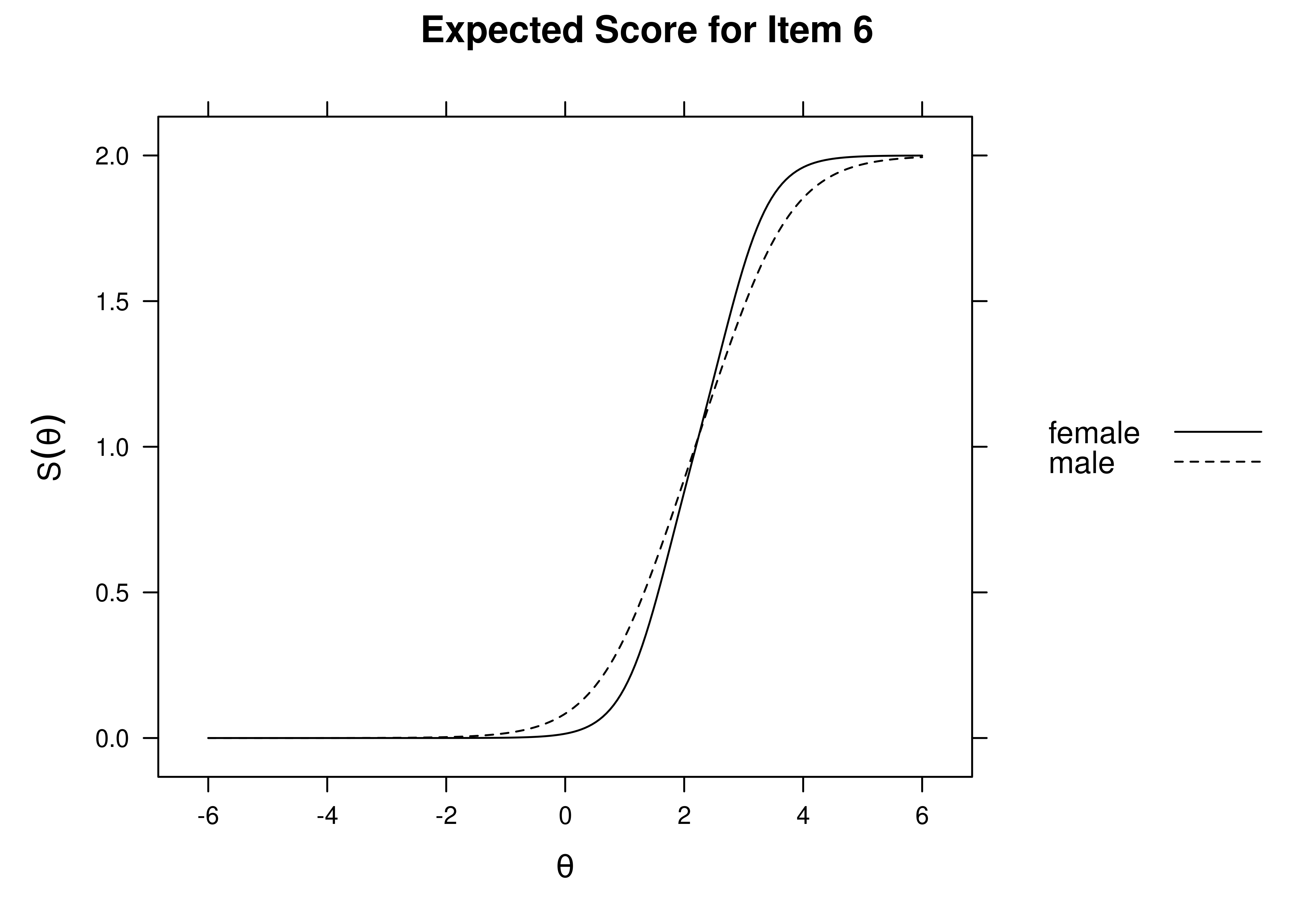
Figure 16.51: Expected Item Score by Sex: Item 6.

Code

itemplot(
  unconstrainedModel,
  "bpi_antisocialT1_7",
  type = "score",
  par.settings = standard.theme("pdf", color = FALSE))

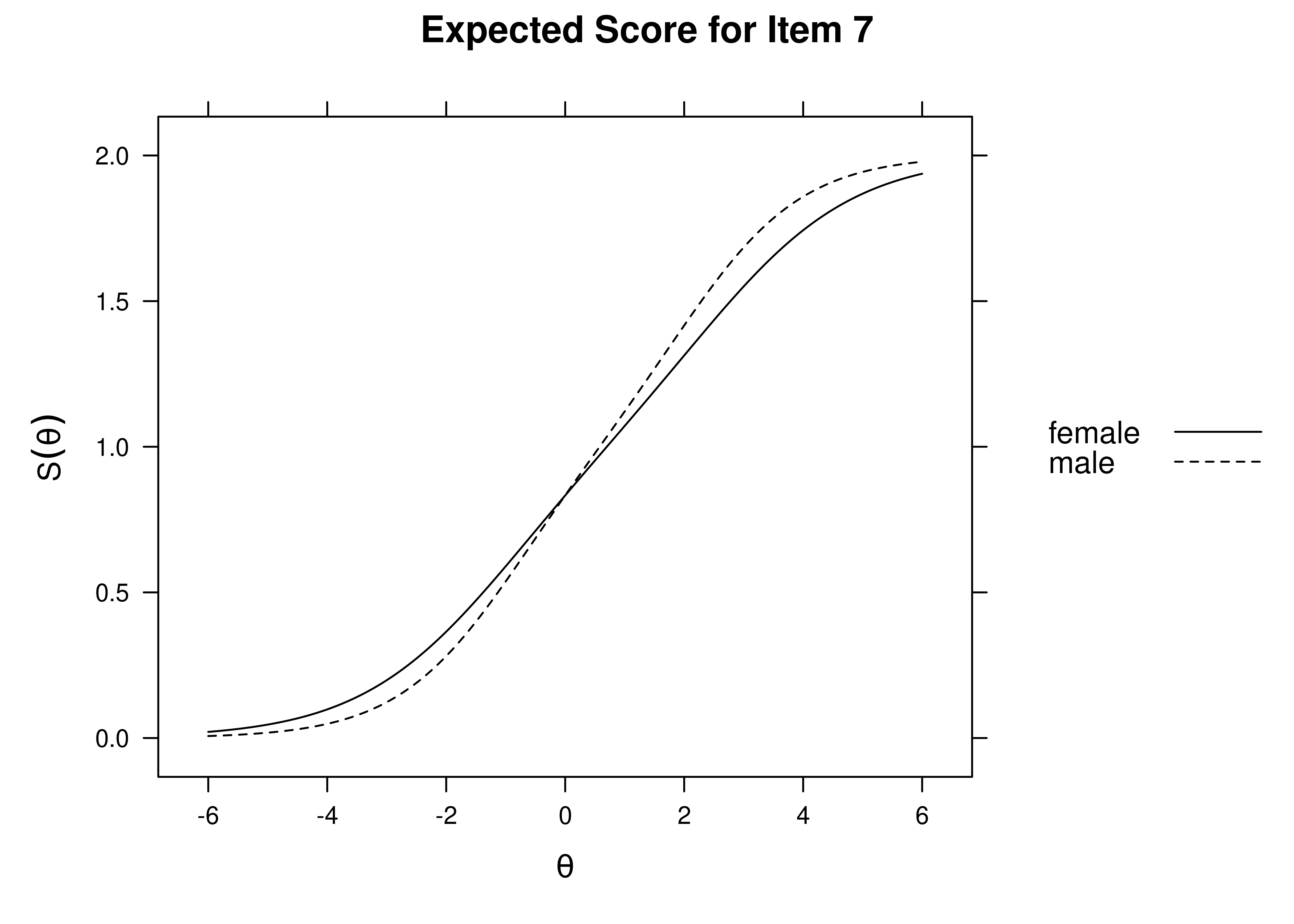
Figure 16.52: Expected Item Score by Sex: Item 7.

16.9.9 Addressing DIF

Based on the analyses above, item 5 shows the largest magnitude of DIF. Specifically, item 5 has a stronger discrimination parameter for women than men. So, we should handle item 5 first. If we deem the DIF for item 5 to be non-negligible, we have three primary options: (1) drop item 5 for both men and women, (2) drop item 5 for men but keep it for women, or (3) freely estimate the parameters (discrimination and difficulty) for item 5 across groups.

16.9.9.1 Drop item for both groups

The first option is to drop item 5 for both men and women groups. You might do this if you want to use a measure that has only those items that function equivalently across groups. However, this can lead to lower reliability and weaker ability to detect individual differences.

Code

constrainedModelDropItem5 <- multipleGroup(
  data = cnlsy[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_6","bpi_antisocialT1_7")],
  model = 1,
  group = cnlsy$sex,
  invariance = c(c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_6","bpi_antisocialT1_7"),
    "free_means", "free_var"),
  SE = TRUE)

coef(constrainedModelDropItem5, simplify = TRUE)

16.9.9.2 Drop item for one group but not another group

A second option is to drop item 5 for men but to keep it for women. You might do this if the item is invalid for men, but still valid for women. The coefficients show an item parameter for item 5 for men, but it was constrained to be equal to the parameter for women, and data were removed from the estimation of item 5 for men.

Code

dropItem5ForMen <- cnlsy
dropItem5ForMen[which(
  dropItem5ForMen$sex == "male"),
  "bpi_antisocialT1_5"] <- NA

constrainedModelDropItem5ForMen <- multipleGroup(
  data = dropItem5ForMen[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7")],
  model = 1,
  group = dropItem5ForMen$sex,
  invariance = c(c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7"),
    "free_means", "free_var"),
  SE = TRUE)

coef(constrainedModelDropItem5ForMen, simplify = TRUE)

16.9.9.3 Freely estimate item to have different parameters across groups

Alternatively, we can resolve DIF by allowing the item to have different parameters (discrimination and difficulty) across both groups. You might do this if the item is valid for both men and women, and it has importantly different item parameters nonetheless.

Code

constrainedModelResolveItem5 <- multipleGroup(
  data = cnlsy[,c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_5","bpi_antisocialT1_6",
    "bpi_antisocialT1_7")],
  model = 1,
  group = cnlsy$sex,
  invariance = c(c(
    "bpi_antisocialT1_1","bpi_antisocialT1_2","bpi_antisocialT1_3",
    "bpi_antisocialT1_4","bpi_antisocialT1_6","bpi_antisocialT1_7"),
    "free_means", "free_var"),
  SE = TRUE)

coef(constrainedModelResolveItem5, simplify = TRUE)

16.9.9.4 Compare model fit

We can compare the model fit against the fully constrained model. In this case, all three of these approaches for handling DIF resulted in improvement in model fit based on AIC and, for the two nested models, the chi-square difference test.

Code

anova(constrainedModel, constrainedModelDropItem5)

Code

anova(constrainedModel, constrainedModelDropItem5ForMen)

Code

anova(constrainedModel, constrainedModelResolveItem5)

16.9.9.5 Next steps

Whichever of these approaches we select, we would then identify and handle the remaining non-negligent DIF sequentially by magnitude. For instance, if we chose to resolve DIF in item 5 by allowing the item to have different parameters across both groups, we would then iteratively drop constraints to see which items continue to show non-negligible DIF.

Code

difDropItemsNew <- DIF(
  constrainedModelResolveItem5,
  c("a1","d1","d2"),
  scheme = "drop",
  simplify = TRUE)

Table 16.1: Differential Item Functioning After Resolving DIF in Item 5.

	groups	converged	AIC	SABIC	HQ	BIC	X2	df	p
bpi_antisocialT1_1	female,male	TRUE	-5.5042001	3.7824138	1.1738421	13.3150439	11.5042001	3	0.0092897
bpi_antisocialT1_2	female,male	TRUE	3.8539227	13.1405366	10.5319649	22.6731667	2.1460773	3	0.5426474
bpi_antisocialT1_3	female,male	TRUE	1.4534865	10.7401004	8.1315287	20.2727305	4.5465135	3	0.2081787
bpi_antisocialT1_4	female,male	TRUE	-26.4683563	-17.1817424	-19.7903141	-7.6491123	32.4683563	3	0.0000004
bpi_antisocialT1_5	female,male	TRUE	0.0000966	0.0000966	0.0000966	0.0000966	-0.0000966	0	NaN
bpi_antisocialT1_6	female,male	TRUE	-9.9043878	-0.6177739	-3.2263456	8.9148562	15.9043878	3	0.0011863
bpi_antisocialT1_7	female,male	TRUE	-16.5941405	-7.3075266	-9.9160983	2.2251035	22.5941405	3	0.0000491

Estimates of DIF after resolving item 5 are in Table 16.1. Of the remaining DIF, item 4 appears to have the largest DIF. If we deem item 4 to show non-negligible DIF, we would address it using one of the three approaches above and then see which items continue to show the largest DIF, address it if necessary, then identify the remaining DIF, etc.

16.10 Measurement/Factorial Invariance

Before making comparisons across groups in terms of associations between constructs or their level on the construct, it is important to establish measurement invariance (also called factorial invariance) across the groups (Millsap, 2011). Tests of measurement invariance are equivalent to tests of differential item functioning. Measurement invariance can help provide greater confidence that the measure functions equivalently across groups, that is, the items have the same strength of association with the latent factor, and the latent factor is on the same metric (i.e., the items have the same level when accounting for the latent factor). For instance, If you observe differences between groups in level of depression without establishing measurement invariance across the groups, you do not know whether the differences observed reflect true group-related differences in depression or differences in the functioning of the measure across the groups.

Measurement invariance can be tested using many methods, including confirmatory factor analysis and IRT. CFA approaches to testing measurement invariance include multi-group CFA (MGCFA), multiple-indicator, multiple-causes (MIMIC) models, moderated nonlinear factor analysis (MNLFA), score-based tests (T. Wang et al., 2014), and the alignment method (Lai, 2021). The IRT approach to testing measurement (non-)invariance is to examine whether items show differential item functioning.

The tests of measurement invariance in confirmatory factor analysis (CFA) models were fit in the lavaan package (Rosseel et al., 2022). The examples were adapted from lavaan documentation: https://lavaan.ugent.be/tutorial/groups.html (archived at https://perma.cc/2FBK-RSAH). Procedures for testing measurement invariance are outlined in Putnick & Bornstein (2016). In addition to nested chi-square difference tests (\(\chi^2_{\text{diff}}\)), I also demonstrate permutation procedures for testing measurement invariance, as described by Jorgensen et al. (2018). Also, you are encouraged to read about MIMIC models (Cheng et al., 2016; W.-C. Wang et al., 2009), score-based tests (T. Wang et al., 2014), and MNLFA that allows for testing measurement invariance across continuous moderators (Bauer et al., 2020; Curran et al., 2014; N. C. Gottfredson et al., 2019). MNLFA is implemented in the mnlfa package (Robitzsch, 2019). You can also generate syntax for conducting MNLFA in Mplus software (Muthén & Muthén, 2019) using the aMNLFA package (V. Cole et al., 2018). The alignment method allows many groups to be compared (Han et al., 2019).

Model fit of nested models can be compared with a chi-square difference test, as a way of testing measurement invariance. In this approach to testing measurement invariance, first model fit is evaluated in a configural invariance model, in which the same number of factors is specified in each group, and which indicators load on which factors are the same in each group. Then, successive constraints are made across groups, including constraining factor loadings, intercepts, and residuals across groups. The metric (“weak factorial”) invariance model is similar to the configural invariance model, but it constrains the factor loadings to be the same across groups. The scalar (“strong factorial”) invariance model keeps the constraints of the metric invariance model, but it also constrains the intercepts to be the same across groups. The residual (“strict factorial”) invariance model keeps the constraints of the scalar invariance model, but it also constrains the residuals to be the same across groups. The fit of each constrained model is compared to the previous model without such constraints. That is, the fit of the metric invariance model is compared to the fit of the configural invariance model, the fit of the scalar invariance model is compared to the fit of the metric invariance model, and the fit of the residual invariance model is compared to the fit of the scalar invariance model.

The chi-square difference test is sensitive to sample size, and trivial differences in fit can be detected with large samples (Cheung & Rensvold, 2002). As a result, researchers also recommend examining change in additional criteria, including CFI, RMSEA, and SRMR (F. F. Chen, 2007). Cheung & Rensvold (2002) recommend a cutoff of \(\Delta \text{CFI} \geq -.01\) for identifying measurement non-invariance. F. F. Chen (2007) recommends the following cutoffs for identifying measurement non-invariance:

• with a small sample size (total \(N \leq 300\)):
  • testing invariance of factor loadings:
    • \(\Delta \text{CFI} \geq -.005\)
    • supplemented by \(\Delta \text{RMSEA} \geq .010\) or \(\Delta \text{SRMR} \geq .025\)
  • testing invariance of intercepts or residuals:
    • \(\Delta \text{CFI} \geq -.005\)
    • supplemented by \(\Delta \text{RMSEA} \geq .010\) or \(\Delta \text{SRMR} \geq .005\)
• with an adequate sample size (total \(N > 300\)):
  • testing invariance of factor loadings:
    • \(\Delta \text{CFI} \geq -.010\)
    • supplemented by \(\Delta \text{RMSEA} \geq .015\) or \(\Delta \text{SRMR} \geq .030\)
  • testing invariance of intercepts or residuals:
    • \(\Delta \text{CFI} \geq -.005\)
    • supplemented by \(\Delta \text{RMSEA} \geq .015\) or \(\Delta \text{SRMR} \geq .010\)

Little et al. (2007) suggested that researchers establish at least partial invariance of factor loadings (metric invariance) to compare covariances across groups, and at least partial invariance of intercepts (scalar invariance) to compare mean levels across groups. Partial invariance refers to invariance with some but not all indicators. So, to examine associations with other variables, invariance of at least some factor loadings would be preferable. To examine differences in level or growth, invariance of at least some factor loadings and intercepts would be preferable. Residual invariance is considered overly restrictive, and it is not generally expected that one establish residual invariance (Little, 2013).

Although measurement invariance is important to test, it is also worth noting that tests of measurement invariance and DIF rest on various fundamentally untestable assumptions related to scale setting (Raykov et al., 2020). For instance, to give the latent factor units, oftentimes researchers set one item’s factor loading to be equal across time (i.e., the marker variable). Results of factorial invariance tests can depend highly on which item is used as the anchor item for setting the scale of the latent factor (Belzak & Bauer, 2020). And subsequent tests of measurement invariance then rest on the fundamentally untestable assumption that changes in the level of the latent factor precipitates the same amount of change in the item across groups. If this scaling is not proper, however, it could lead to improper conclusions. Researchers are, therefore, not conclusively able to establish measurement invariance.

Several possible approaches may help address this. First, it can be helpful to place greater focus on degree of measurement invariance and confidence (rather than presence versus absence of measurement invariance). To the extent that non-invariance is trivial in effect size, it provides the researcher with greater confidence that they can use the measure to assess a construct in a comparable way over time. A number of studies describe how to test the effect size of measurement invariance (Gunn et al., 2020; e.g., Liu et al., 2017) or differential item functioning (Gonzalez & Pelham, 2021; e.g., Meade, 2010). Second, there may be important robustness checks. I describe each in greater detail below. One important sensitivity analysis could be to see if measurement invariance holds when using different marker variables. This would provide greater evidence that their apparent measurement invariance was not specific to one marker variable (i.e., one particular set of assumptions). A second robustness check would be to use effects coding, in which the average of items’ factor loadings is equal to 1, so the metric of the latent variable is on the metric of all of the items rather than just one item (Little et al., 2006). A third robustness check would be to use regularization, which is an alternative method to select the anchor items and to identify differential item functioning based on a machine learning technique that applies penalization to remove parameters that have little impact on model fit (Bauer et al., 2020; Belzak & Bauer, 2020).

Another issue with measurement invariance is that the null hypothesis that adding constraints across groups will not worsen fit is likely always false, because there are often at least slight differences across groups in factor loadings, intercepts, or residuals that reflect sampling variability. However, we are not interested in trivial differences across groups that reflect sampling variability. Instead, we are interested in the extent to which there are substantive, meaningful differences across the groups of large enough magnitude to be practically meaningful. Thus, it can also be helpful to consider whether the measures show approximate measurement invariance (Van De Schoot et al., 2015). For details on how to test approximate measurement invariance, see Van De Schoot et al. (2013).

When detecting measurement non-invariance in a given parameter (e.g., factor loadings, intercepts, or residuals), one can identify the specific items that show measurement non-invariance in one of two primary ways: (1) starting with a model that allows the given parameter to differ across groups, a researcher can iteratively add constraints to identify the item(s) for which measurement invariance fails, or (2) starting with a model that constrains the given parameter to be the same across groups, a researcher can iteratively remove constraints to identify the item(s) for which measurement invariance becomes established (and by process of elimination, the items for which measurement invariance does not become established).

Approaches to addressing measurement non-invariance are described in Section 16.5.1. If we identify that an item shows non-negligible non-invariance, we have three primary options (described above): (1) drop the item for both groups, (2) drop the item for one group but keep it for the other group, or (3) freely estimate the parameters (factor loadings and/or intercepts) for the item across groups.

Using the traditional chi-square difference test, tests of measurement invariance compare the model fit to a model with perfect fit. As the sample size grows larger, smaller differences in model fit will be detected as significant, thus rejecting measurement invariance even if the model fits well. So, it can also be useful to compare the model fit to a null hypothesis that the fit is poor, instead of the null hypothesis that the model is a perfect fit. Chi-square equivalence tests use the poor model fit as the null hypothesis. Thus, a significant chi-square equivalence test suggests that the equality constraints are plausible, providing support for the alternative hypothesis that the model fit is acceptable (Counsell et al., 2020).

16.10.1 Specify Models

16.10.1.1 Null Model

Fix residual variances and intercepts of manifest variables to be equal across groups.

Code

nullModel <- '
#Fix residual variances of manifest variables to be equal across groups
x1 ~~ c(psi1, psi1)*x1
x2 ~~ c(psi2, psi2)*x2
x3 ~~ c(psi3, psi3)*x3
x4 ~~ c(psi4, psi4)*x4
x5 ~~ c(psi5, psi5)*x5
x6 ~~ c(psi6, psi6)*x6
x7 ~~ c(psi7, psi7)*x7
x8 ~~ c(psi8, psi8)*x8
x9 ~~ c(psi9, psi9)*x9

#Fix intercepts of manifest variables to be equal across groups
x1 ~ c(tau1, tau1)*1
x2 ~ c(tau2, tau2)*1
x3 ~ c(tau3, tau3)*1
x4 ~ c(tau4, tau4)*1
x5 ~ c(tau5, tau5)*1
x6 ~ c(tau6, tau6)*1
x7 ~ c(tau7, tau7)*1
x8 ~ c(tau8, tau8)*1
x9 ~ c(tau9, tau9)*1
'

16.10.1.2 CFA Model

Code

cfaModel <- '
 #Factor loadings
 visual  =~ x1 + x2 + x3
 textual =~ x4 + x5 + x6
 speed   =~ x7 + x8 + x9
'

16.10.1.3 Configural Invariance

Specify the same number of factors in each group, and which indicators load on which factors are the same in each group.

Code

cfaModel_configuralInvariance <- '
 #Factor loadings (free the factor loading of the first indicator)
 visual  =~ NA*x1 + x2 + x3
 textual =~ NA*x4 + x5 + x6
 speed   =~ NA*x7 + x8 + x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one
 visual ~~ 1*visual
 textual ~~ 1*textual
 speed ~~ 1*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Free intercepts of manifest variables
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

16.10.1.4 Metric (“Weak Factorial”) Invariance

Specify invariance of factor loadings across groups.

Code

cfaModel_metricInvariance <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Free intercepts of manifest variables
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

16.10.1.5 Scalar (“Strong Factorial”) Invariance

Specify invariance of factor loadings and intercepts across groups.

Code

cfaModel_scalarInvariance <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero in group 1; free latent means in group 2
 visual ~ c(0, NA)*1
 textual ~ c(0, NA)*1
 speed ~ c(0, NA)*1
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ c(intx2, intx2)*1
 x3 ~ c(intx3, intx3)*1
 x4 ~ c(intx4, intx4)*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

16.10.1.6 Residual (“Strict Factorial”) Invariance

Specify invariance of factor loadings, intercepts, and residuals across groups.

Code

cfaModel_residualInvariance <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ c(0, NA)*1
 textual ~ c(0, NA)*1
 speed ~ c(0, NA)*1
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Fix residual variances of manifest variables across groups
 x1 ~~ c(residx1, residx1)*x1
 x2 ~~ c(residx2, residx2)*x2
 x3 ~~ c(residx3, residx3)*x3
 x4 ~~ c(residx4, residx4)*x4
 x5 ~~ c(residx5, residx5)*x5
 x6 ~~ c(residx6, residx6)*x6
 x7 ~~ c(residx7, residx7)*x7
 x8 ~~ c(residx8, residx8)*x8
 x9 ~~ c(residx9, residx9)*x9
 
 #Fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ c(intx2, intx2)*1
 x3 ~ c(intx3, intx3)*1
 x4 ~ c(intx4, intx4)*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

16.10.2 Specify the Fit Indices of Interest

Code

myAFIs <- c("chisq", "chisq.scaled",
            "rmsea", "cfi", "tli", "srmr",
            "rmsea.robust", "cfi.robust", "tli.robust")
moreAFIs <- NULL # c("gammaHat","gammaHat.scaled")

16.10.3 Null Model

16.10.3.1 Fit the Model

Code

nullModelFit <- lavaan(
  nullModel,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

16.10.3.2 Model Summary

Code

summary(
  nullModelFit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 39 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        36
  Number of equality constraints                    18

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                              1034.341    1001.376
  Degrees of freedom                                90          90
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  1.033
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                    477.005     477.005
    Grant-White                                524.371     524.371

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.000       0.000
  Tucker-Lewis Index (TLI)                       0.122       0.129
                                                                  
  Robust Comparative Fit Index (CFI)                         0.000
  Robust Tucker-Lewis Index (TLI)                            0.125

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -4111.291   -4111.291
  Scaling correction factor                                  0.520
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                8258.582    8258.582
  Bayesian (BIC)                              8325.310    8325.310
  Sample-size adjusted Bayesian (SABIC)       8268.224    8268.224

Root Mean Square Error of Approximation:

  RMSEA                                          0.264       0.259
  90 Percent confidence interval - lower         0.250       0.245
  90 Percent confidence interval - upper         0.279       0.274
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    1.000       1.000
                                                                  
  Robust RMSEA                                               0.267
  90 Percent confidence interval - lower                     0.252
  90 Percent confidence interval - upper                     0.282
  P-value H_0: Robust RMSEA <= 0.050                         0.000
  P-value H_0: Robust RMSEA >= 0.080                         1.000

Standardized Root Mean Square Residual:

  SRMR                                           0.284       0.284

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    x1      (tau1)    4.935    0.067   73.255    0.000    4.935    4.236
    x2      (tau2)    6.085    0.068   89.601    0.000    6.085    5.173
    x3      (tau3)    2.261    0.066   34.411    0.000    2.261    2.000
    x4      (tau4)    3.050    0.067   45.313    0.000    3.050    2.634
    x5      (tau5)    4.332    0.074   58.509    0.000    4.332    3.389
    x6      (tau6)    2.195    0.063   34.800    0.000    2.195    2.013
    x7      (tau7)    4.196    0.063   66.358    0.000    4.196    3.850
    x8      (tau8)    5.524    0.059   94.261    0.000    5.524    5.451
    x9      (tau9)    5.378    0.059   91.869    0.000    5.378    5.322

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    x1      (psi1)    1.357    0.120   11.283    0.000    1.357    1.000
    x2      (psi2)    1.384    0.123   11.273    0.000    1.384    1.000
    x3      (psi3)    1.278    0.077   16.500    0.000    1.278    1.000
    x4      (psi4)    1.341    0.114   11.780    0.000    1.341    1.000
    x5      (psi5)    1.634    0.116   14.144    0.000    1.634    1.000
    x6      (psi6)    1.189    0.116   10.243    0.000    1.189    1.000
    x7      (psi7)    1.188    0.090   13.206    0.000    1.188    1.000
    x8      (psi8)    1.027    0.106    9.674    0.000    1.027    1.000
    x9      (psi9)    1.021    0.090   11.389    0.000    1.021    1.000


Group 2 [Grant-White]:

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    x1      (tau1)    4.935    0.067   73.255    0.000    4.935    4.236
    x2      (tau2)    6.085    0.068   89.601    0.000    6.085    5.173
    x3      (tau3)    2.261    0.066   34.411    0.000    2.261    2.000
    x4      (tau4)    3.050    0.067   45.313    0.000    3.050    2.634
    x5      (tau5)    4.332    0.074   58.509    0.000    4.332    3.389
    x6      (tau6)    2.195    0.063   34.800    0.000    2.195    2.013
    x7      (tau7)    4.196    0.063   66.358    0.000    4.196    3.850
    x8      (tau8)    5.524    0.059   94.261    0.000    5.524    5.451
    x9      (tau9)    5.378    0.059   91.869    0.000    5.378    5.322

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    x1      (psi1)    1.357    0.120   11.283    0.000    1.357    1.000
    x2      (psi2)    1.384    0.123   11.273    0.000    1.384    1.000
    x3      (psi3)    1.278    0.077   16.500    0.000    1.278    1.000
    x4      (psi4)    1.341    0.114   11.780    0.000    1.341    1.000
    x5      (psi5)    1.634    0.116   14.144    0.000    1.634    1.000
    x6      (psi6)    1.189    0.116   10.243    0.000    1.189    1.000
    x7      (psi7)    1.188    0.090   13.206    0.000    1.188    1.000
    x8      (psi8)    1.027    0.106    9.674    0.000    1.027    1.000
    x9      (psi9)    1.021    0.090   11.389    0.000    1.021    1.000

16.10.4 Configural Invariance

Specify the same number of factors in each group, and which indicators load on which factors are the same in each group.

16.10.4.1 Model Syntax

Code

configuralInvarianceModel <- measEq.syntax(
  configural.model = cfaModel,
  data = HolzingerSwineford1939,
  ID.fac = "std.lv",
  group = "school")

Code

cat(as.character(configuralInvarianceModel))

## LOADINGS:

visual =~ c(NA, NA)*x1 + c(lambda.1_1.g1, lambda.1_1.g2)*x1
visual =~ c(NA, NA)*x2 + c(lambda.2_1.g1, lambda.2_1.g2)*x2
visual =~ c(NA, NA)*x3 + c(lambda.3_1.g1, lambda.3_1.g2)*x3
textual =~ c(NA, NA)*x4 + c(lambda.4_2.g1, lambda.4_2.g2)*x4
textual =~ c(NA, NA)*x5 + c(lambda.5_2.g1, lambda.5_2.g2)*x5
textual =~ c(NA, NA)*x6 + c(lambda.6_2.g1, lambda.6_2.g2)*x6
speed =~ c(NA, NA)*x7 + c(lambda.7_3.g1, lambda.7_3.g2)*x7
speed =~ c(NA, NA)*x8 + c(lambda.8_3.g1, lambda.8_3.g2)*x8
speed =~ c(NA, NA)*x9 + c(lambda.9_3.g1, lambda.9_3.g2)*x9

## INTERCEPTS:

x1 ~ c(NA, NA)*1 + c(nu.1.g1, nu.1.g2)*1
x2 ~ c(NA, NA)*1 + c(nu.2.g1, nu.2.g2)*1
x3 ~ c(NA, NA)*1 + c(nu.3.g1, nu.3.g2)*1
x4 ~ c(NA, NA)*1 + c(nu.4.g1, nu.4.g2)*1
x5 ~ c(NA, NA)*1 + c(nu.5.g1, nu.5.g2)*1
x6 ~ c(NA, NA)*1 + c(nu.6.g1, nu.6.g2)*1
x7 ~ c(NA, NA)*1 + c(nu.7.g1, nu.7.g2)*1
x8 ~ c(NA, NA)*1 + c(nu.8.g1, nu.8.g2)*1
x9 ~ c(NA, NA)*1 + c(nu.9.g1, nu.9.g2)*1

## UNIQUE-FACTOR VARIANCES:

x1 ~~ c(NA, NA)*x1 + c(theta.1_1.g1, theta.1_1.g2)*x1
x2 ~~ c(NA, NA)*x2 + c(theta.2_2.g1, theta.2_2.g2)*x2
x3 ~~ c(NA, NA)*x3 + c(theta.3_3.g1, theta.3_3.g2)*x3
x4 ~~ c(NA, NA)*x4 + c(theta.4_4.g1, theta.4_4.g2)*x4
x5 ~~ c(NA, NA)*x5 + c(theta.5_5.g1, theta.5_5.g2)*x5
x6 ~~ c(NA, NA)*x6 + c(theta.6_6.g1, theta.6_6.g2)*x6
x7 ~~ c(NA, NA)*x7 + c(theta.7_7.g1, theta.7_7.g2)*x7
x8 ~~ c(NA, NA)*x8 + c(theta.8_8.g1, theta.8_8.g2)*x8
x9 ~~ c(NA, NA)*x9 + c(theta.9_9.g1, theta.9_9.g2)*x9

## LATENT MEANS/INTERCEPTS:

visual ~ c(0, 0)*1 + c(alpha.1.g1, alpha.1.g2)*1
textual ~ c(0, 0)*1 + c(alpha.2.g1, alpha.2.g2)*1
speed ~ c(0, 0)*1 + c(alpha.3.g1, alpha.3.g2)*1

## COMMON-FACTOR VARIANCES:

visual ~~ c(1, 1)*visual + c(psi.1_1.g1, psi.1_1.g2)*visual
textual ~~ c(1, 1)*textual + c(psi.2_2.g1, psi.2_2.g2)*textual
speed ~~ c(1, 1)*speed + c(psi.3_3.g1, psi.3_3.g2)*speed

## COMMON-FACTOR COVARIANCES:

visual ~~ c(NA, NA)*textual + c(psi.2_1.g1, psi.2_1.g2)*textual
visual ~~ c(NA, NA)*speed + c(psi.3_1.g1, psi.3_1.g2)*speed
textual ~~ c(NA, NA)*speed + c(psi.3_2.g1, psi.3_2.g2)*speed

Code

configuralInvarianceSyntax <- as.character(configuralInvarianceModel)

16.10.4.1.1 Summary of Model Features

Code

summary(configuralInvarianceModel)

This lavaan model syntax specifies a CFA with 9 manifest indicators of 3 common factor(s).

To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed.

Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor:

   visual textual speed
x1 num                 
x2 num                 
x3 num                 
x4        num          
x5        num          
x6        num          
x7                num  
x8                num  
x9                num  


This model hypothesizes only configural invariance.

16.10.4.1.2 Model Syntax in Table Form

Code

lavaanify(cfaModel, ngroups = 2)

16.10.4.2 Fit the Model

Code

configuralInvarianceModel_fit <- cfa(
  configuralInvarianceSyntax,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

Code

configuralInvarianceModelFullSyntax_fit <- lavaan(
  cfaModel_configuralInvariance,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

16.10.4.3 Model Summary

Code

summary(
  configuralInvarianceModel_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 64 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        60

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               109.425     114.970
  Degrees of freedom                                48          48
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.952
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     63.000      63.000
    Grant-White                                 51.970      51.970

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.929       0.920
  Tucker-Lewis Index (TLI)                       0.893       0.880
                                                                  
  Robust Comparative Fit Index (CFI)                         0.929
  Robust Tucker-Lewis Index (TLI)                            0.893

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3648.833   -3648.833
  Scaling correction factor                                  1.100
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7417.666    7417.666
  Bayesian (BIC)                              7640.092    7640.092
  Sample-size adjusted Bayesian (SABIC)       7449.806    7449.806

Root Mean Square Error of Approximation:

  RMSEA                                          0.092       0.096
  90 Percent confidence interval - lower         0.069       0.073
  90 Percent confidence interval - upper         0.115       0.120
  P-value H_0: RMSEA <= 0.050                    0.002       0.001
  P-value H_0: RMSEA >= 0.080                    0.821       0.883
                                                                  
  Robust RMSEA                                               0.093
  90 Percent confidence interval - lower                     0.070
  90 Percent confidence interval - upper                     0.117
  P-value H_0: Robust RMSEA <= 0.050                         0.002
  P-value H_0: Robust RMSEA >= 0.080                         0.833

Standardized Root Mean Square Residual:

  SRMR                                           0.066       0.066

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.999    0.172    5.810    0.000    0.999    0.846
    x2      (l.2_)    0.443    0.147    3.022    0.003    0.443    0.361
    x3      (l.3_)    0.624    0.134    4.662    0.000    0.624    0.541
  textual =~                                                            
    x4      (l.4_)    0.922    0.085   10.830    0.000    0.922    0.811
    x5      (l.5_)    1.126    0.072   15.723    0.000    1.126    0.864
    x6      (l.6_)    0.833    0.081   10.242    0.000    0.833    0.843
  speed =~                                                              
    x7      (l.7_)    0.570    0.119    4.790    0.000    0.570    0.527
    x8      (l.8_)    0.676    0.110    6.133    0.000    0.676    0.688
    x9      (l.9_)    0.587    0.118    4.998    0.000    0.587    0.589

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.473    0.095    4.951    0.000    0.473    0.473
    speed  (p.3_1)    0.319    0.148    2.150    0.032    0.319    0.319
  textual ~~                                                            
    speed  (p.3_2)    0.311    0.100    3.099    0.002    0.311    0.311

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (n.1.)    4.947    0.095   52.269    0.000    4.947    4.191
   .x2      (n.2.)    5.984    0.098   60.949    0.000    5.984    4.880
   .x3      (n.3.)    2.510    0.093   26.912    0.000    2.510    2.178
   .x4      (n.4.)    2.814    0.091   30.873    0.000    2.814    2.476
   .x5      (n.5.)    4.002    0.105   38.256    0.000    4.002    3.070
   .x6      (n.6.)    1.929    0.079   24.376    0.000    1.929    1.953
   .x7      (n.7.)    4.439    0.087   51.126    0.000    4.439    4.104
   .x8      (n.8.)    5.563    0.079   70.133    0.000    5.563    5.663
   .x9      (n.9.)    5.426    0.080   67.537    0.000    5.426    5.443
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.396    0.298    1.330    0.183    0.396    0.284
   .x2      (t.2_)    1.308    0.175    7.482    0.000    1.308    0.870
   .x3      (t.3_)    0.939    0.158    5.959    0.000    0.939    0.707
   .x4      (t.4_)    0.441    0.072    6.091    0.000    0.441    0.342
   .x5      (t.5_)    0.431    0.083    5.169    0.000    0.431    0.254
   .x6      (t.6_)    0.282    0.056    5.063    0.000    0.282    0.289
   .x7      (t.7_)    0.845    0.132    6.394    0.000    0.845    0.723
   .x8      (t.8_)    0.509    0.109    4.673    0.000    0.509    0.527
   .x9      (t.9_)    0.649    0.134    4.824    0.000    0.649    0.653
    visual  (p.1_)    1.000                               1.000    1.000
    textual (p.2_)    1.000                               1.000    1.000
    speed   (p.3_)    1.000                               1.000    1.000

R-Square:
                   Estimate
    x1                0.716
    x2                0.130
    x3                0.293
    x4                0.658
    x5                0.746
    x6                0.711
    x7                0.277
    x8                0.473
    x9                0.347


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.781    0.128    6.099    0.000    0.781    0.679
    x2      (l.2_)    0.566    0.103    5.489    0.000    0.566    0.510
    x3      (l.3_)    0.717    0.100    7.165    0.000    0.717    0.690
  textual =~                                                            
    x4      (l.4_)    0.958    0.083   11.489    0.000    0.958    0.856
    x5      (l.5_)    0.973    0.090   10.798    0.000    0.973    0.835
    x6      (l.6_)    0.947    0.088   10.753    0.000    0.947    0.830
  speed =~                                                              
    x7      (l.7_)    0.672    0.090    7.446    0.000    0.672    0.649
    x8      (l.8_)    0.833    0.112    7.447    0.000    0.833    0.796
    x9      (l.9_)    0.732    0.124    5.924    0.000    0.732    0.714

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.545    0.096    5.648    0.000    0.545    0.545
    speed  (p.3_1)    0.531    0.148    3.593    0.000    0.531    0.531
  textual ~~                                                            
    speed  (p.3_2)    0.339    0.142    2.392    0.017    0.339    0.339

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (n.1.)    4.929    0.096   51.433    0.000    4.929    4.286
   .x2      (n.2.)    6.198    0.092   67.052    0.000    6.198    5.587
   .x3      (n.3.)    1.992    0.086   23.048    0.000    1.992    1.916
   .x4      (n.4.)    3.317    0.093   35.551    0.000    3.317    2.966
   .x5      (n.5.)    4.712    0.096   49.039    0.000    4.712    4.045
   .x6      (n.6.)    2.466    0.094   26.150    0.000    2.466    2.163
   .x7      (n.7.)    3.923    0.087   45.300    0.000    3.923    3.793
   .x8      (n.8.)    5.488    0.087   63.174    0.000    5.488    5.246
   .x9      (n.9.)    5.338    0.085   62.640    0.000    5.338    5.210
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.712    0.183    3.884    0.000    0.712    0.538
   .x2      (t.2_)    0.911    0.143    6.364    0.000    0.911    0.740
   .x3      (t.3_)    0.566    0.123    4.601    0.000    0.566    0.524
   .x4      (t.4_)    0.333    0.066    5.025    0.000    0.333    0.267
   .x5      (t.5_)    0.411    0.074    5.570    0.000    0.411    0.303
   .x6      (t.6_)    0.404    0.078    5.182    0.000    0.404    0.311
   .x7      (t.7_)    0.619    0.101    6.105    0.000    0.619    0.578
   .x8      (t.8_)    0.401    0.160    2.512    0.012    0.401    0.366
   .x9      (t.9_)    0.514    0.140    3.684    0.000    0.514    0.490
    visual  (p.1_)    1.000                               1.000    1.000
    textual (p.2_)    1.000                               1.000    1.000
    speed   (p.3_)    1.000                               1.000    1.000

R-Square:
                   Estimate
    x1                0.462
    x2                0.260
    x3                0.476
    x4                0.733
    x5                0.697
    x6                0.689
    x7                0.422
    x8                0.634
    x9                0.510

Code

summary(
  configuralInvarianceModelFullSyntax_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 64 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        60

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               109.425     114.970
  Degrees of freedom                                48          48
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.952
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     63.000      63.000
    Grant-White                                 51.970      51.970

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.929       0.920
  Tucker-Lewis Index (TLI)                       0.893       0.880
                                                                  
  Robust Comparative Fit Index (CFI)                         0.929
  Robust Tucker-Lewis Index (TLI)                            0.893

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3648.833   -3648.833
  Scaling correction factor                                  1.100
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7417.666    7417.666
  Bayesian (BIC)                              7640.092    7640.092
  Sample-size adjusted Bayesian (SABIC)       7449.806    7449.806

Root Mean Square Error of Approximation:

  RMSEA                                          0.092       0.096
  90 Percent confidence interval - lower         0.069       0.073
  90 Percent confidence interval - upper         0.115       0.120
  P-value H_0: RMSEA <= 0.050                    0.002       0.001
  P-value H_0: RMSEA >= 0.080                    0.821       0.883
                                                                  
  Robust RMSEA                                               0.093
  90 Percent confidence interval - lower                     0.070
  90 Percent confidence interval - upper                     0.117
  P-value H_0: Robust RMSEA <= 0.050                         0.002
  P-value H_0: Robust RMSEA >= 0.080                         0.833

Standardized Root Mean Square Residual:

  SRMR                                           0.066       0.066

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1                0.999    0.172    5.810    0.000    0.999    0.846
    x2                0.443    0.147    3.022    0.003    0.443    0.361
    x3                0.624    0.134    4.662    0.000    0.624    0.541
  textual =~                                                            
    x4                0.922    0.085   10.830    0.000    0.922    0.811
    x5                1.126    0.072   15.723    0.000    1.126    0.864
    x6                0.833    0.081   10.242    0.000    0.833    0.843
  speed =~                                                              
    x7                0.570    0.119    4.790    0.000    0.570    0.527
    x8                0.676    0.110    6.133    0.000    0.676    0.688
    x9                0.587    0.118    4.998    0.000    0.587    0.589

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.473    0.095    4.951    0.000    0.473    0.473
    speed             0.319    0.148    2.150    0.032    0.319    0.319
  textual ~~                                                            
    speed             0.311    0.100    3.099    0.002    0.311    0.311

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1                4.947    0.095   52.269    0.000    4.947    4.191
   .x2                5.984    0.098   60.949    0.000    5.984    4.880
   .x3                2.510    0.093   26.912    0.000    2.510    2.178
   .x4                2.814    0.091   30.873    0.000    2.814    2.476
   .x5                4.002    0.105   38.256    0.000    4.002    3.070
   .x6                1.929    0.079   24.376    0.000    1.929    1.953
   .x7                4.439    0.087   51.126    0.000    4.439    4.104
   .x8                5.563    0.079   70.133    0.000    5.563    5.663
   .x9                5.426    0.080   67.537    0.000    5.426    5.443

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            1.000                               1.000    1.000
    textual           1.000                               1.000    1.000
    speed             1.000                               1.000    1.000
   .x1                0.396    0.298    1.330    0.183    0.396    0.284
   .x2                1.308    0.175    7.482    0.000    1.308    0.870
   .x3                0.939    0.158    5.959    0.000    0.939    0.707
   .x4                0.441    0.072    6.091    0.000    0.441    0.342
   .x5                0.431    0.083    5.169    0.000    0.431    0.254
   .x6                0.282    0.056    5.063    0.000    0.282    0.289
   .x7                0.845    0.132    6.394    0.000    0.845    0.723
   .x8                0.509    0.109    4.673    0.000    0.509    0.527
   .x9                0.649    0.134    4.824    0.000    0.649    0.653

R-Square:
                   Estimate
    x1                0.716
    x2                0.130
    x3                0.293
    x4                0.658
    x5                0.746
    x6                0.711
    x7                0.277
    x8                0.473
    x9                0.347


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1                0.781    0.128    6.099    0.000    0.781    0.679
    x2                0.566    0.103    5.489    0.000    0.566    0.510
    x3                0.717    0.100    7.165    0.000    0.717    0.690
  textual =~                                                            
    x4                0.958    0.083   11.489    0.000    0.958    0.856
    x5                0.973    0.090   10.798    0.000    0.973    0.835
    x6                0.947    0.088   10.753    0.000    0.947    0.830
  speed =~                                                              
    x7                0.672    0.090    7.446    0.000    0.672    0.649
    x8                0.833    0.112    7.447    0.000    0.833    0.796
    x9                0.732    0.124    5.924    0.000    0.732    0.714

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.545    0.096    5.648    0.000    0.545    0.545
    speed             0.531    0.148    3.593    0.000    0.531    0.531
  textual ~~                                                            
    speed             0.339    0.142    2.392    0.017    0.339    0.339

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1                4.929    0.096   51.433    0.000    4.929    4.286
   .x2                6.198    0.092   67.052    0.000    6.198    5.587
   .x3                1.992    0.086   23.048    0.000    1.992    1.916
   .x4                3.317    0.093   35.551    0.000    3.317    2.966
   .x5                4.712    0.096   49.039    0.000    4.712    4.045
   .x6                2.466    0.094   26.150    0.000    2.466    2.163
   .x7                3.923    0.087   45.300    0.000    3.923    3.793
   .x8                5.488    0.087   63.174    0.000    5.488    5.246
   .x9                5.338    0.085   62.640    0.000    5.338    5.210

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            1.000                               1.000    1.000
    textual           1.000                               1.000    1.000
    speed             1.000                               1.000    1.000
   .x1                0.712    0.183    3.884    0.000    0.712    0.538
   .x2                0.911    0.143    6.364    0.000    0.911    0.740
   .x3                0.566    0.123    4.601    0.000    0.566    0.524
   .x4                0.333    0.066    5.025    0.000    0.333    0.267
   .x5                0.411    0.074    5.570    0.000    0.411    0.303
   .x6                0.404    0.078    5.182    0.000    0.404    0.311
   .x7                0.619    0.101    6.105    0.000    0.619    0.578
   .x8                0.401    0.160    2.512    0.012    0.401    0.366
   .x9                0.514    0.140    3.684    0.000    0.514    0.490

R-Square:
                   Estimate
    x1                0.462
    x2                0.260
    x3                0.476
    x4                0.733
    x5                0.697
    x6                0.689
    x7                0.422
    x8                0.634
    x9                0.510

16.10.4.4 Model Fit

You can specify the null model as the baseline model using: baseline.model = nullModelFit

Code

fitMeasures(configuralInvarianceModel_fit)

                         npar                          fmin 
                       60.000                         0.182 
                        chisq                            df 
                      109.425                        48.000 
                       pvalue                  chisq.scaled 
                        0.000                       114.970 
                    df.scaled                 pvalue.scaled 
                       48.000                         0.000 
         chisq.scaling.factor                baseline.chisq 
                        0.952                       932.665 
                  baseline.df               baseline.pvalue 
                       72.000                         0.000 
        baseline.chisq.scaled            baseline.df.scaled 
                      909.019                        72.000 
       baseline.pvalue.scaled baseline.chisq.scaling.factor 
                        0.000                         1.026 
                          cfi                           tli 
                        0.929                         0.893 
                   cfi.scaled                    tli.scaled 
                        0.920                         0.880 
                   cfi.robust                    tli.robust 
                        0.929                         0.893 
                         nnfi                           rfi 
                        0.893                         0.824 
                          nfi                          pnfi 
                        0.883                         0.588 
                          ifi                           rni 
                        0.931                         0.929 
                  nnfi.scaled                    rfi.scaled 
                        0.880                         0.810 
                   nfi.scaled                   pnfi.scaled 
                        0.874                         0.582 
                   ifi.scaled                    rni.scaled 
                        0.922                         0.920 
                  nnfi.robust                    rni.robust 
                        0.893                         0.929 
                         logl             unrestricted.logl 
                    -3648.833                     -3594.120 
                          aic                           bic 
                     7417.666                      7640.092 
                       ntotal                          bic2 
                      301.000                      7449.806 
            scaling.factor.h1             scaling.factor.h0 
                        1.034                         1.100 
                        rmsea                rmsea.ci.lower 
                        0.092                         0.069 
               rmsea.ci.upper                rmsea.ci.level 
                        0.115                         0.900 
                 rmsea.pvalue                rmsea.close.h0 
                        0.002                         0.050 
        rmsea.notclose.pvalue             rmsea.notclose.h0 
                        0.821                         0.080 
                 rmsea.scaled         rmsea.ci.lower.scaled 
                        0.096                         0.073 
        rmsea.ci.upper.scaled           rmsea.pvalue.scaled 
                        0.120                         0.001 
 rmsea.notclose.pvalue.scaled                  rmsea.robust 
                        0.883                         0.093 
        rmsea.ci.lower.robust         rmsea.ci.upper.robust 
                        0.070                         0.117 
          rmsea.pvalue.robust  rmsea.notclose.pvalue.robust 
                        0.002                         0.833 
                          rmr                    rmr_nomean 
                        0.081                         0.089 
                         srmr                  srmr_bentler 
                        0.066                         0.066 
          srmr_bentler_nomean                          crmr 
                        0.072                         0.072 
                  crmr_nomean                    srmr_mplus 
                        0.080                         0.066 
            srmr_mplus_nomean                         cn_05 
                        0.072                       180.268 
                        cn_01                           gfi 
                      203.682                         0.995 
                         agfi                          pgfi 
                        0.989                         0.442 
                          mfi                          ecvi 
                        0.903                         0.762 

Code

configuralInvarianceModelFitIndices <- fitMeasures(
  configuralInvarianceModel_fit)[c(
    "cfi.robust", "rmsea.robust", "srmr")]

configuralInvarianceModel_chisquare <- fitMeasures(
  configuralInvarianceModel_fit)[c("chisq.scaled")]

configuralInvarianceModel_chisquareScaling <- fitMeasures(
  configuralInvarianceModel_fit)[c("chisq.scaling.factor")]

configuralInvarianceModel_df <- fitMeasures(
  configuralInvarianceModel_fit)[c("df.scaled")]

configuralInvarianceModel_N <- lavInspect(
  configuralInvarianceModel_fit,
  what = "ntotal")

16.10.4.5 Effect size of non-invariance

16.10.4.5.1 dMACS

The effect size of measurement non-invariance, as described by Nye et al. (2019), was calculated using the dmacs package (Dueber, 2019).

Code

lavaan_dmacs(configuralInvarianceModel_fit)

$DMACS
      visual   textual     speed
x1 0.1865718        NA        NA
x2 0.2102487        NA        NA
x3 0.4774264        NA        NA
x4        NA 0.4450412        NA
x5        NA 0.5889006        NA
x6        NA 0.5196869        NA
x7        NA        NA 0.4941585
x8        NA        NA 0.1714779
x9        NA        NA 0.1669673

$ItemDeltaMean
        visual   textual       speed
x1 -0.01829609        NA          NA
x2  0.21407860        NA          NA
x3 -0.51808612        NA          NA
x4          NA 0.5031129          NA
x5          NA 0.7100353          NA
x6          NA 0.5368256          NA
x7          NA        NA -0.51547978
x8          NA        NA -0.07512450
x9          NA        NA -0.08770776

$MeanDiff
    visual    textual      speed 
-0.3223036  1.7499738 -0.6783120 

16.10.4.6 Equivalence Test

The petersenlab package (Petersen, 2024b) contains the equiv_chi() function from Counsell et al. (2020) that performs an equivalence test: https://osf.io/cqu8v. An equivalence test evaluates the null hypothesis that a model is equivalent to another model. In this case, the equivalence test evaluates the null hypothesis that a model is equivalent to another model in terms of (poor) fit. Here, we operationalize a mediocre-fitting model as a model whose RMSEA is .08 or greater. So, the equivalence test evaluates whether our invariance model fits significantly better than a mediocre-fitting model. Thus, a statistically significant p-value indicates that our invariance model fits significantly better than the mediocre-fitting model (i.e., that invariance is established), whereas a non-significant p-value indicates that our invariance model does not fit significantly better than the mediocre-fitting model (i.e., that invariance is failed).

The chi-square equivalence test is non-significant, suggesting that the model fit of the configural invariance model is not acceptable (i.e., it is not better than the mediocre-fitting model). In other words, configural invariance failed.

Code

equiv_chi(
  alpha = .05,
  chi = configuralInvarianceModel_chisquare,
  df = configuralInvarianceModel_df,
  m = 2,
  N_sample = configuralInvarianceModel_N,
  popRMSEA = .08)

16.10.4.7 Permutation Test

Permutation procedures for testing measurement invariance are described in Jorgensen et al. (2018). The permutation test evaluates the null hypothesis that the model fit is not worse than the best-possible fitting model. A significant p-value indicates that the model fits significanlty worse than the best-possible fitting model. A non-significant p-value indicates that the model does not fit significantly worse than the best-possible fitting model.

Code

numPermutations <- 100

For reproducibility, I set the seed below. Using the same seed will yield the same answer every time. There is nothing special about this particular seed. You can specify the null model as the baseline model using: baseline.model = nullModelFit. Warning: this code takes a while to run based on \(100\) iterations. You can reduce the number of iterations to be faster.

Code

set.seed(52242)
configuralInvarianceTest <- permuteMeasEq(
  nPermute = numPermutations,
  modelType = "mgcfa",
  con = configuralInvarianceModel_fit,
  uncon = NULL,
  AFIs = myAFIs,
  moreAFIs = moreAFIs,
  parallelType = "multicore", #only 'snow' works on Windows, but right now, it is throwing an error
  iseed = 52242)

Code

RNGkind("default", "default", "default")
set.seed(52242)

configuralInvarianceTest

Omnibus p value based on parametric chi-squared difference test:

Chisq diff    Df diff Pr(>Chisq) 
    114.97      48.00       0.00 


Omnibus p values based on nonparametric permutation method: 

             AFI.Difference p.value
chisq               109.425    0.17
chisq.scaled        114.970    0.15
rmsea                 0.092    0.17
cfi                   0.929    0.15
tli                   0.893    0.15
srmr                  0.066    0.15
rmsea.robust          0.093    0.15
cfi.robust            0.929    0.14
tli.robust            0.893    0.14

The p-values are non-significant, indicating that the model does not fit significantly worse than the best-possible fitting model. In other words, configural invariance held.

16.10.4.8 Internal Consistency Reliability

Internal consistency reliability of items composing the latent factors, as quantified by omega (\(\omega\)) and average variance extracted (AVE), was estimated using the semTools package (Jorgensen et al., 2021).

Code

compRelSEM(configuralInvarianceModel_fit)

Code

AVE(configuralInvarianceModel_fit)

16.10.4.9 Path Diagram

A path diagram of the model generated using the semPlot package (Epskamp, 2022) is in the figures below (“1” = group 1; “2” = group 2).

Code

semPaths(
  configuralInvarianceModel_fit,
  what = "est",
  layout = "tree2",
  ask = FALSE,
  edge.label.cex = 1.2)

Figure 16.53: Configural Invariance Model in Confirmatory Factor Analysis (1 = Group 1; 2 = Group 2).

Figure 16.54: Configural Invariance Model in Confirmatory Factor Analysis (1 = Group 1; 2 = Group 2).

16.10.5 Metric (“Weak Factorial”) Invariance Model

Specify invariance of factor loadings across groups.

16.10.5.1 Model Syntax

Code

metricInvarianceModel <- measEq.syntax(
  configural.model = cfaModel,
  data = HolzingerSwineford1939,
  ID.fac = "std.lv",
  group = "school",
  group.equal = "loadings")

Code

cat(as.character(metricInvarianceModel))

## LOADINGS:

visual =~ c(NA, NA)*x1 + c(lambda.1_1, lambda.1_1)*x1
visual =~ c(NA, NA)*x2 + c(lambda.2_1, lambda.2_1)*x2
visual =~ c(NA, NA)*x3 + c(lambda.3_1, lambda.3_1)*x3
textual =~ c(NA, NA)*x4 + c(lambda.4_2, lambda.4_2)*x4
textual =~ c(NA, NA)*x5 + c(lambda.5_2, lambda.5_2)*x5
textual =~ c(NA, NA)*x6 + c(lambda.6_2, lambda.6_2)*x6
speed =~ c(NA, NA)*x7 + c(lambda.7_3, lambda.7_3)*x7
speed =~ c(NA, NA)*x8 + c(lambda.8_3, lambda.8_3)*x8
speed =~ c(NA, NA)*x9 + c(lambda.9_3, lambda.9_3)*x9

## INTERCEPTS:

x1 ~ c(NA, NA)*1 + c(nu.1.g1, nu.1.g2)*1
x2 ~ c(NA, NA)*1 + c(nu.2.g1, nu.2.g2)*1
x3 ~ c(NA, NA)*1 + c(nu.3.g1, nu.3.g2)*1
x4 ~ c(NA, NA)*1 + c(nu.4.g1, nu.4.g2)*1
x5 ~ c(NA, NA)*1 + c(nu.5.g1, nu.5.g2)*1
x6 ~ c(NA, NA)*1 + c(nu.6.g1, nu.6.g2)*1
x7 ~ c(NA, NA)*1 + c(nu.7.g1, nu.7.g2)*1
x8 ~ c(NA, NA)*1 + c(nu.8.g1, nu.8.g2)*1
x9 ~ c(NA, NA)*1 + c(nu.9.g1, nu.9.g2)*1

## UNIQUE-FACTOR VARIANCES:

x1 ~~ c(NA, NA)*x1 + c(theta.1_1.g1, theta.1_1.g2)*x1
x2 ~~ c(NA, NA)*x2 + c(theta.2_2.g1, theta.2_2.g2)*x2
x3 ~~ c(NA, NA)*x3 + c(theta.3_3.g1, theta.3_3.g2)*x3
x4 ~~ c(NA, NA)*x4 + c(theta.4_4.g1, theta.4_4.g2)*x4
x5 ~~ c(NA, NA)*x5 + c(theta.5_5.g1, theta.5_5.g2)*x5
x6 ~~ c(NA, NA)*x6 + c(theta.6_6.g1, theta.6_6.g2)*x6
x7 ~~ c(NA, NA)*x7 + c(theta.7_7.g1, theta.7_7.g2)*x7
x8 ~~ c(NA, NA)*x8 + c(theta.8_8.g1, theta.8_8.g2)*x8
x9 ~~ c(NA, NA)*x9 + c(theta.9_9.g1, theta.9_9.g2)*x9

## LATENT MEANS/INTERCEPTS:

visual ~ c(0, 0)*1 + c(alpha.1.g1, alpha.1.g2)*1
textual ~ c(0, 0)*1 + c(alpha.2.g1, alpha.2.g2)*1
speed ~ c(0, 0)*1 + c(alpha.3.g1, alpha.3.g2)*1

## COMMON-FACTOR VARIANCES:

visual ~~ c(1, NA)*visual + c(psi.1_1.g1, psi.1_1.g2)*visual
textual ~~ c(1, NA)*textual + c(psi.2_2.g1, psi.2_2.g2)*textual
speed ~~ c(1, NA)*speed + c(psi.3_3.g1, psi.3_3.g2)*speed

## COMMON-FACTOR COVARIANCES:

visual ~~ c(NA, NA)*textual + c(psi.2_1.g1, psi.2_1.g2)*textual
visual ~~ c(NA, NA)*speed + c(psi.3_1.g1, psi.3_1.g2)*speed
textual ~~ c(NA, NA)*speed + c(psi.3_2.g1, psi.3_2.g2)*speed

Code

metricInvarianceSyntax <- as.character(metricInvarianceModel)

16.10.5.1.1 Summary of Model Features

Code

summary(metricInvarianceModel)

This lavaan model syntax specifies a CFA with 9 manifest indicators of 3 common factor(s).

To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed.

Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor:

   visual textual speed
x1 num                 
x2 num                 
x3 num                 
x4        num          
x5        num          
x6        num          
x7                num  
x8                num  
x9                num  

The following types of parameter were constrained to equality across groups:

    loadings

16.10.5.2 Model Syntax in Table Form

Code

lavaanify(metricInvarianceModel, ngroups = 2)

Code

lavaanify(cfaModel_metricInvariance, ngroups = 2)

16.10.5.3 Fit the Model

Code

metricInvarianceModel_fit <- cfa(
  metricInvarianceSyntax,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

Code

metricInvarianceModelFullSyntax_fit <- lavaan(
  cfaModel_metricInvariance,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

16.10.5.4 Model Summary

Code

summary(
  metricInvarianceModel_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 73 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        63
  Number of equality constraints                     9

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               116.313     117.955
  Degrees of freedom                                54          54
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.986
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     64.366      64.366
    Grant-White                                 53.590      53.590

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.928       0.924
  Tucker-Lewis Index (TLI)                       0.903       0.898
                                                                  
  Robust Comparative Fit Index (CFI)                         0.928
  Robust Tucker-Lewis Index (TLI)                            0.905

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3652.277   -3652.277
  Scaling correction factor                                  0.928
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7412.554    7412.554
  Bayesian (BIC)                              7612.738    7612.738
  Sample-size adjusted Bayesian (SABIC)       7441.480    7441.480

Root Mean Square Error of Approximation:

  RMSEA                                          0.088       0.089
  90 Percent confidence interval - lower         0.066       0.067
  90 Percent confidence interval - upper         0.109       0.111
  P-value H_0: RMSEA <= 0.050                    0.004       0.003
  P-value H_0: RMSEA >= 0.080                    0.730       0.757
                                                                  
  Robust RMSEA                                               0.088
  90 Percent confidence interval - lower                     0.066
  90 Percent confidence interval - upper                     0.111
  P-value H_0: Robust RMSEA <= 0.050                         0.004
  P-value H_0: Robust RMSEA >= 0.080                         0.740

Standardized Root Mean Square Residual:

  SRMR                                           0.069       0.069

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.885    0.122    7.258    0.000    0.885    0.759
    x2      (l.2_)    0.536    0.088    6.106    0.000    0.536    0.432
    x3      (l.3_)    0.707    0.087    8.148    0.000    0.707    0.608
  textual =~                                                            
    x4      (l.4_)    0.935    0.072   12.929    0.000    0.935    0.813
    x5      (l.5_)    1.045    0.076   13.740    0.000    1.045    0.832
    x6      (l.6_)    0.874    0.070   12.496    0.000    0.874    0.865
  speed =~                                                              
    x7      (l.7_)    0.550    0.075    7.346    0.000    0.550    0.510
    x8      (l.8_)    0.675    0.087    7.784    0.000    0.675    0.686
    x9      (l.9_)    0.602    0.088    6.867    0.000    0.602    0.603

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.473    0.105    4.484    0.000    0.473    0.473
    speed  (p.3_1)    0.347    0.125    2.778    0.005    0.347    0.347
  textual ~~                                                            
    speed  (p.3_2)    0.320    0.096    3.342    0.001    0.320    0.320

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (n.1.)    4.948    0.095   52.314    0.000    4.948    4.243
   .x2      (n.2.)    5.984    0.098   60.949    0.000    5.984    4.823
   .x3      (n.3.)    2.510    0.093   26.891    0.000    2.510    2.157
   .x4      (n.4.)    2.814    0.091   30.886    0.000    2.814    2.448
   .x5      (n.5.)    4.002    0.105   38.265    0.000    4.002    3.186
   .x6      (n.6.)    1.929    0.079   24.377    0.000    1.929    1.907
   .x7      (n.7.)    4.439    0.087   51.128    0.000    4.439    4.117
   .x8      (n.8.)    5.564    0.079   70.170    0.000    5.564    5.655
   .x9      (n.9.)    5.426    0.080   67.539    0.000    5.426    5.435
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.577    0.166    3.482    0.000    0.577    0.424
   .x2      (t.2_)    1.252    0.162    7.718    0.000    1.252    0.813
   .x3      (t.3_)    0.853    0.127    6.737    0.000    0.853    0.630
   .x4      (t.4_)    0.447    0.072    6.189    0.000    0.447    0.339
   .x5      (t.5_)    0.486    0.075    6.445    0.000    0.486    0.308
   .x6      (t.6_)    0.258    0.057    4.499    0.000    0.258    0.252
   .x7      (t.7_)    0.860    0.114    7.549    0.000    0.860    0.739
   .x8      (t.8_)    0.512    0.097    5.296    0.000    0.512    0.529
   .x9      (t.9_)    0.635    0.118    5.376    0.000    0.635    0.637
    visual  (p.1_)    1.000                               1.000    1.000
    textual (p.2_)    1.000                               1.000    1.000
    speed   (p.3_)    1.000                               1.000    1.000

R-Square:
                   Estimate
    x1                0.576
    x2                0.187
    x3                0.370
    x4                0.661
    x5                0.692
    x6                0.748
    x7                0.261
    x8                0.471
    x9                0.363


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.885    0.122    7.258    0.000    0.844    0.723
    x2      (l.2_)    0.536    0.088    6.106    0.000    0.512    0.467
    x3      (l.3_)    0.707    0.087    8.148    0.000    0.675    0.655
  textual =~                                                            
    x4      (l.4_)    0.935    0.072   12.929    0.000    0.937    0.846
    x5      (l.5_)    1.045    0.076   13.740    0.000    1.047    0.864
    x6      (l.6_)    0.874    0.070   12.496    0.000    0.876    0.798
  speed =~                                                              
    x7      (l.7_)    0.550    0.075    7.346    0.000    0.674    0.649
    x8      (l.8_)    0.675    0.087    7.784    0.000    0.826    0.790
    x9      (l.9_)    0.602    0.088    6.867    0.000    0.736    0.719

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.520    0.134    3.867    0.000    0.544    0.544
    speed  (p.3_1)    0.638    0.211    3.023    0.002    0.546    0.546
  textual ~~                                                            
    speed  (p.3_2)    0.429    0.193    2.219    0.026    0.350    0.350

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (n.1.)    4.930    0.096   51.453    0.000    4.930    4.220
   .x2      (n.2.)    6.198    0.092   67.063    0.000    6.198    5.654
   .x3      (n.3.)    1.992    0.086   23.042    0.000    1.992    1.934
   .x4      (n.4.)    3.318    0.093   35.501    0.000    3.318    2.997
   .x5      (n.5.)    4.714    0.097   48.693    0.000    4.714    3.891
   .x6      (n.6.)    2.467    0.094   26.165    0.000    2.467    2.246
   .x7      (n.7.)    3.923    0.087   45.299    0.000    3.923    3.782
   .x8      (n.8.)    5.488    0.087   63.174    0.000    5.488    5.250
   .x9      (n.9.)    5.338    0.085   62.628    0.000    5.338    5.216
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.652    0.168    3.877    0.000    0.652    0.478
   .x2      (t.2_)    0.940    0.145    6.473    0.000    0.940    0.782
   .x3      (t.3_)    0.606    0.113    5.376    0.000    0.606    0.571
   .x4      (t.4_)    0.348    0.066    5.257    0.000    0.348    0.284
   .x5      (t.5_)    0.371    0.074    5.021    0.000    0.371    0.253
   .x6      (t.6_)    0.439    0.076    5.738    0.000    0.439    0.364
   .x7      (t.7_)    0.622    0.098    6.338    0.000    0.622    0.578
   .x8      (t.8_)    0.410    0.148    2.765    0.006    0.410    0.375
   .x9      (t.9_)    0.505    0.128    3.957    0.000    0.505    0.482
    visual  (p.1_)    0.910    0.234    3.895    0.000    1.000    1.000
    textual (p.2_)    1.004    0.191    5.257    0.000    1.000    1.000
    speed   (p.3_)    1.498    0.357    4.201    0.000    1.000    1.000

R-Square:
                   Estimate
    x1                0.522
    x2                0.218
    x3                0.429
    x4                0.716
    x5                0.747
    x6                0.636
    x7                0.422
    x8                0.625
    x9                0.518

Code

summary(
  metricInvarianceModelFullSyntax_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 73 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        63
  Number of equality constraints                     9

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               116.313     117.955
  Degrees of freedom                                54          54
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.986
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     64.366      64.366
    Grant-White                                 53.590      53.590

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.928       0.924
  Tucker-Lewis Index (TLI)                       0.903       0.898
                                                                  
  Robust Comparative Fit Index (CFI)                         0.928
  Robust Tucker-Lewis Index (TLI)                            0.905

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3652.277   -3652.277
  Scaling correction factor                                  0.928
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7412.554    7412.554
  Bayesian (BIC)                              7612.738    7612.738
  Sample-size adjusted Bayesian (SABIC)       7441.480    7441.480

Root Mean Square Error of Approximation:

  RMSEA                                          0.088       0.089
  90 Percent confidence interval - lower         0.066       0.067
  90 Percent confidence interval - upper         0.109       0.111
  P-value H_0: RMSEA <= 0.050                    0.004       0.003
  P-value H_0: RMSEA >= 0.080                    0.730       0.757
                                                                  
  Robust RMSEA                                               0.088
  90 Percent confidence interval - lower                     0.066
  90 Percent confidence interval - upper                     0.111
  P-value H_0: Robust RMSEA <= 0.050                         0.004
  P-value H_0: Robust RMSEA >= 0.080                         0.740

Standardized Root Mean Square Residual:

  SRMR                                           0.069       0.069

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.885    0.122    7.258    0.000    0.885    0.759
    x2      (lmb2)    0.536    0.088    6.106    0.000    0.536    0.432
    x3      (lmb3)    0.707    0.087    8.148    0.000    0.707    0.608
  textual =~                                                            
    x4      (lmb4)    0.935    0.072   12.929    0.000    0.935    0.813
    x5      (lmb5)    1.045    0.076   13.740    0.000    1.045    0.832
    x6      (lmb6)    0.874    0.070   12.496    0.000    0.874    0.865
  speed =~                                                              
    x7      (lmb7)    0.550    0.075    7.346    0.000    0.550    0.510
    x8      (lmb8)    0.675    0.087    7.784    0.000    0.675    0.686
    x9      (lmb9)    0.602    0.088    6.867    0.000    0.602    0.603

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.473    0.105    4.484    0.000    0.473    0.473
    speed             0.347    0.125    2.778    0.005    0.347    0.347
  textual ~~                                                            
    speed             0.320    0.096    3.342    0.001    0.320    0.320

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1                4.948    0.095   52.314    0.000    4.948    4.243
   .x2                5.984    0.098   60.949    0.000    5.984    4.823
   .x3                2.510    0.093   26.891    0.000    2.510    2.157
   .x4                2.814    0.091   30.886    0.000    2.814    2.448
   .x5                4.002    0.105   38.265    0.000    4.002    3.186
   .x6                1.929    0.079   24.377    0.000    1.929    1.907
   .x7                4.439    0.087   51.128    0.000    4.439    4.117
   .x8                5.564    0.079   70.170    0.000    5.564    5.655
   .x9                5.426    0.080   67.539    0.000    5.426    5.435

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            1.000                               1.000    1.000
    textual           1.000                               1.000    1.000
    speed             1.000                               1.000    1.000
   .x1                0.577    0.166    3.482    0.000    0.577    0.424
   .x2                1.252    0.162    7.718    0.000    1.252    0.813
   .x3                0.853    0.127    6.737    0.000    0.853    0.630
   .x4                0.447    0.072    6.189    0.000    0.447    0.339
   .x5                0.486    0.075    6.445    0.000    0.486    0.308
   .x6                0.258    0.057    4.499    0.000    0.258    0.252
   .x7                0.860    0.114    7.549    0.000    0.860    0.739
   .x8                0.512    0.097    5.296    0.000    0.512    0.529
   .x9                0.635    0.118    5.376    0.000    0.635    0.637

R-Square:
                   Estimate
    x1                0.576
    x2                0.187
    x3                0.370
    x4                0.661
    x5                0.692
    x6                0.748
    x7                0.261
    x8                0.471
    x9                0.363


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.885    0.122    7.258    0.000    0.844    0.723
    x2      (lmb2)    0.536    0.088    6.106    0.000    0.512    0.467
    x3      (lmb3)    0.707    0.087    8.148    0.000    0.675    0.655
  textual =~                                                            
    x4      (lmb4)    0.935    0.072   12.929    0.000    0.937    0.846
    x5      (lmb5)    1.045    0.076   13.740    0.000    1.047    0.864
    x6      (lmb6)    0.874    0.070   12.496    0.000    0.876    0.798
  speed =~                                                              
    x7      (lmb7)    0.550    0.075    7.346    0.000    0.674    0.649
    x8      (lmb8)    0.675    0.087    7.784    0.000    0.826    0.790
    x9      (lmb9)    0.602    0.088    6.867    0.000    0.736    0.719

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.520    0.134    3.867    0.000    0.544    0.544
    speed             0.638    0.211    3.023    0.002    0.546    0.546
  textual ~~                                                            
    speed             0.429    0.193    2.219    0.026    0.350    0.350

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1                4.930    0.096   51.453    0.000    4.930    4.220
   .x2                6.198    0.092   67.063    0.000    6.198    5.654
   .x3                1.992    0.086   23.042    0.000    1.992    1.934
   .x4                3.318    0.093   35.501    0.000    3.318    2.997
   .x5                4.714    0.097   48.693    0.000    4.714    3.891
   .x6                2.467    0.094   26.165    0.000    2.467    2.246
   .x7                3.923    0.087   45.299    0.000    3.923    3.782
   .x8                5.488    0.087   63.174    0.000    5.488    5.250
   .x9                5.338    0.085   62.628    0.000    5.338    5.216

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.910    0.234    3.895    0.000    1.000    1.000
    textual           1.004    0.191    5.257    0.000    1.000    1.000
    speed             1.498    0.357    4.201    0.000    1.000    1.000
   .x1                0.652    0.168    3.877    0.000    0.652    0.478
   .x2                0.940    0.145    6.473    0.000    0.940    0.782
   .x3                0.606    0.113    5.376    0.000    0.606    0.571
   .x4                0.348    0.066    5.257    0.000    0.348    0.284
   .x5                0.371    0.074    5.021    0.000    0.371    0.253
   .x6                0.439    0.076    5.738    0.000    0.439    0.364
   .x7                0.622    0.098    6.338    0.000    0.622    0.578
   .x8                0.410    0.148    2.765    0.006    0.410    0.375
   .x9                0.505    0.128    3.957    0.000    0.505    0.482

R-Square:
                   Estimate
    x1                0.522
    x2                0.218
    x3                0.429
    x4                0.716
    x5                0.747
    x6                0.636
    x7                0.422
    x8                0.625
    x9                0.518

16.10.5.5 Model Fit

You can specify the null model as the baseline model using: baseline.model = nullModelFit

Code

fitMeasures(metricInvarianceModel_fit)

                         npar                          fmin 
                       54.000                         0.193 
                        chisq                            df 
                      116.313                        54.000 
                       pvalue                  chisq.scaled 
                        0.000                       117.955 
                    df.scaled                 pvalue.scaled 
                       54.000                         0.000 
         chisq.scaling.factor                baseline.chisq 
                        0.986                       932.665 
                  baseline.df               baseline.pvalue 
                       72.000                         0.000 
        baseline.chisq.scaled            baseline.df.scaled 
                      909.019                        72.000 
       baseline.pvalue.scaled baseline.chisq.scaling.factor 
                        0.000                         1.026 
                          cfi                           tli 
                        0.928                         0.903 
                   cfi.scaled                    tli.scaled 
                        0.924                         0.898 
                   cfi.robust                    tli.robust 
                        0.928                         0.905 
                         nnfi                           rfi 
                        0.903                         0.834 
                          nfi                          pnfi 
                        0.875                         0.656 
                          ifi                           rni 
                        0.929                         0.928 
                  nnfi.scaled                    rfi.scaled 
                        0.898                         0.827 
                   nfi.scaled                   pnfi.scaled 
                        0.870                         0.653 
                   ifi.scaled                    rni.scaled 
                        0.925                         0.924 
                  nnfi.robust                    rni.robust 
                        0.905                         0.928 
                         logl             unrestricted.logl 
                    -3652.277                     -3594.120 
                          aic                           bic 
                     7412.554                      7612.738 
                       ntotal                          bic2 
                      301.000                      7441.480 
            scaling.factor.h1             scaling.factor.h0 
                        1.034                         0.928 
                        rmsea                rmsea.ci.lower 
                        0.088                         0.066 
               rmsea.ci.upper                rmsea.ci.level 
                        0.109                         0.900 
                 rmsea.pvalue                rmsea.close.h0 
                        0.004                         0.050 
        rmsea.notclose.pvalue             rmsea.notclose.h0 
                        0.730                         0.080 
                 rmsea.scaled         rmsea.ci.lower.scaled 
                        0.089                         0.067 
        rmsea.ci.upper.scaled           rmsea.pvalue.scaled 
                        0.111                         0.003 
 rmsea.notclose.pvalue.scaled                  rmsea.robust 
                        0.757                         0.088 
        rmsea.ci.lower.robust         rmsea.ci.upper.robust 
                        0.066                         0.111 
          rmsea.pvalue.robust  rmsea.notclose.pvalue.robust 
                        0.004                         0.740 
                          rmr                    rmr_nomean 
                        0.085                         0.093 
                         srmr                  srmr_bentler 
                        0.069                         0.069 
          srmr_bentler_nomean                          crmr 
                        0.075                         0.073 
                  crmr_nomean                    srmr_mplus 
                        0.081                         0.072 
            srmr_mplus_nomean                         cn_05 
                        0.074                       187.721 
                        cn_01                           gfi 
                      210.793                         0.995 
                         agfi                          pgfi 
                        0.989                         0.497 
                          mfi                          ecvi 
                        0.902                         0.745 

Code

metricInvarianceModelFitIndices <- fitMeasures(
  metricInvarianceModel_fit)[c(
    "cfi.robust", "rmsea.robust", "srmr")]

metricInvarianceModel_chisquare <- fitMeasures(
  metricInvarianceModel_fit)[c("chisq.scaled")]

metricInvarianceModel_chisquareScaling <- fitMeasures(
  metricInvarianceModel_fit)[c("chisq.scaling.factor")]

metricInvarianceModel_df <- fitMeasures(
  metricInvarianceModel_fit)[c("df.scaled")]

metricInvarianceModel_N <- lavInspect(
  metricInvarianceModel_fit, what = "ntotal")

16.10.5.6 Compare Model Fit

16.10.5.6.1 Nested Model (\(\chi^2\)) Difference Test

The configural invariance model and the metric (“weak factorial”) invariance model are considered “nested” models. The metric invariance model is nested within the configural invariance model because the configural invariance model includes all of the terms of the metric invariance model along with additional terms. Model fit of nested models can be compared with a chi-square difference test, also known as a likelihood ratio test or deviance test. A significant chi-square difference test would indicate that the simplified model with additional constraints (the metric invariance model) is significantly worse fitting than the more complex model that has fewer constraints (the configural invariance model).

Code

anova(configuralInvarianceModel_fit, metricInvarianceModel_fit)

The metric invariance model did not fit significantly worse than the configural invariance model, so metric invariance held. This provides evidence of measurement invariance of factor loadings across groups. Measurement invariance of factor loadings across groups provides support for examining whether the groups show different associations of the factor with other constructs (Little et al., 2007).

The petersenlab package (Petersen, 2024b) contains the satorraBentlerScaledChiSquareDifferenceTestStatistic() function that performs a Satorra-Bentler scaled chi-square difference test: Below is a Satorra-Bentler scaled chi-square difference test, where \(c0\) and \(c1\) are the scaling correction factor for the nested model and comparison model, respectively; \(d0\) and \(d1\) are the degrees of freedom of the nested model and comparison model, respectively; and \(T0\) and \(T1\) are the chi-square values of the nested model and comparison model, respectively.

Code

metricInvarianceModel_chisquareDiff <- 
  satorraBentlerScaledChiSquareDifferenceTestStatistic(
    T0 = metricInvarianceModel_chisquare,
    c0 = metricInvarianceModel_chisquareScaling,
    d0 = metricInvarianceModel_df,
    T1 = configuralInvarianceModel_chisquare,
    c1 = configuralInvarianceModel_chisquareScaling,
    d1 = configuralInvarianceModel_df)

metricInvarianceModel_chisquareDiff

chisq.scaled 
    5.464443 

16.10.5.6.2 Compare Other Fit Criteria

Code

round(metricInvarianceModelFitIndices - configuralInvarianceModelFitIndices, digits = 3)

  cfi.robust rmsea.robust         srmr 
      -0.001       -0.005        0.003 

16.10.5.6.3 Score-Based Test

Score-based tests of measurement invariance are implemented using the strucchange package and are described by T. Wang et al. (2014).

Code

coef(metricInvarianceModel_fit)

  lambda.1_1   lambda.2_1   lambda.3_1   lambda.4_2   lambda.5_2   lambda.6_2 
       0.885        0.536        0.707        0.935        1.045        0.874 
  lambda.7_3   lambda.8_3   lambda.9_3      nu.1.g1      nu.2.g1      nu.3.g1 
       0.550        0.675        0.602        4.948        5.984        2.510 
     nu.4.g1      nu.5.g1      nu.6.g1      nu.7.g1      nu.8.g1      nu.9.g1 
       2.814        4.002        1.929        4.439        5.564        5.426 
theta.1_1.g1 theta.2_2.g1 theta.3_3.g1 theta.4_4.g1 theta.5_5.g1 theta.6_6.g1 
       0.577        1.252        0.853        0.447        0.486        0.258 
theta.7_7.g1 theta.8_8.g1 theta.9_9.g1   psi.2_1.g1   psi.3_1.g1   psi.3_2.g1 
       0.860        0.512        0.635        0.473        0.347        0.320 
  lambda.1_1   lambda.2_1   lambda.3_1   lambda.4_2   lambda.5_2   lambda.6_2 
       0.885        0.536        0.707        0.935        1.045        0.874 
  lambda.7_3   lambda.8_3   lambda.9_3      nu.1.g2      nu.2.g2      nu.3.g2 
       0.550        0.675        0.602        4.930        6.198        1.992 
     nu.4.g2      nu.5.g2      nu.6.g2      nu.7.g2      nu.8.g2      nu.9.g2 
       3.318        4.714        2.467        3.923        5.488        5.338 
theta.1_1.g2 theta.2_2.g2 theta.3_3.g2 theta.4_4.g2 theta.5_5.g2 theta.6_6.g2 
       0.652        0.940        0.606        0.348        0.371        0.439 
theta.7_7.g2 theta.8_8.g2 theta.9_9.g2   psi.1_1.g2   psi.2_2.g2   psi.3_3.g2 
       0.622        0.410        0.505        0.910        1.004        1.498 
  psi.2_1.g2   psi.3_1.g2   psi.3_2.g2 
       0.520        0.638        0.429 

Code

coef(metricInvarianceModel_fit)[1:9]

lambda.1_1 lambda.2_1 lambda.3_1 lambda.4_2 lambda.5_2 lambda.6_2 lambda.7_3 
 0.8850052  0.5363099  0.7072357  0.9347277  1.0449934  0.8743059  0.5504042 
lambda.8_3 lambda.9_3 
 0.6751277  0.6015120 

Code

strucchange::sctest(
  metricInvarianceModel_fit,
  order.by = HolzingerSwineford1939$school,
  parm = 1:9,
  functional = "LMuo")

    M-fluctuation test

data:  metricInvarianceModel_fit
f(efp) = 5.0601, p-value = 0.829

A score-based test and expected parameter change (EPC) estimates (Oberski, 2014; Oberski et al., 2015) are provided by the lavaan package (Rosseel et al., 2022).

Code

lavTestScore(
  metricInvarianceModel_fit,
  epc = TRUE
)

$test

total score test:

   test    X2 df p.value
1 score 6.199  9    0.72

$uni

univariate score tests:

   lhs op   rhs    X2 df p.value
1 .p1. == .p37. 1.303  1   0.254
2 .p2. == .p38. 0.468  1   0.494
3 .p3. == .p39. 0.334  1   0.563
4 .p4. == .p40. 0.314  1   0.575
5 .p5. == .p41. 4.447  1   0.035
6 .p6. == .p42. 2.539  1   0.111
7 .p7. == .p43. 0.027  1   0.869
8 .p8. == .p44. 0.005  1   0.942
9 .p9. == .p45. 0.007  1   0.932

$epc

expected parameter changes (epc) and expected parameter values (epv):

       lhs op     rhs block group free        label plabel   est    epc   epv
1   visual =~      x1     1     1    1   lambda.1_1   .p1. 0.885  0.072 0.957
2   visual =~      x2     1     1    2   lambda.2_1   .p2. 0.536 -0.060 0.476
3   visual =~      x3     1     1    3   lambda.3_1   .p3. 0.707 -0.052 0.655
4  textual =~      x4     1     1    4   lambda.4_2   .p4. 0.935 -0.018 0.916
5  textual =~      x5     1     1    5   lambda.5_2   .p5. 1.045  0.081 1.126
6  textual =~      x6     1     1    6   lambda.6_2   .p6. 0.874 -0.042 0.832
7    speed =~      x7     1     1    7   lambda.7_3   .p7. 0.550  0.013 0.563
8    speed =~      x8     1     1    8   lambda.8_3   .p8. 0.675 -0.004 0.671
9    speed =~      x9     1     1    9   lambda.9_3   .p9. 0.602 -0.004 0.597
10      x1 ~1             1     1   10      nu.1.g1  .p10. 4.948  0.000 4.948
11      x2 ~1             1     1   11      nu.2.g1  .p11. 5.984  0.000 5.984
12      x3 ~1             1     1   12      nu.3.g1  .p12. 2.510  0.000 2.510
13      x4 ~1             1     1   13      nu.4.g1  .p13. 2.814  0.000 2.814
14      x5 ~1             1     1   14      nu.5.g1  .p14. 4.002  0.000 4.002
15      x6 ~1             1     1   15      nu.6.g1  .p15. 1.929  0.000 1.929
16      x7 ~1             1     1   16      nu.7.g1  .p16. 4.439  0.000 4.439
17      x8 ~1             1     1   17      nu.8.g1  .p17. 5.564  0.000 5.564
18      x9 ~1             1     1   18      nu.9.g1  .p18. 5.426  0.000 5.426
19      x1 ~~      x1     1     1   19 theta.1_1.g1  .p19. 0.577 -0.094 0.483
20      x2 ~~      x2     1     1   20 theta.2_2.g1  .p20. 1.252  0.029 1.280
21      x3 ~~      x3     1     1   21 theta.3_3.g1  .p21. 0.853  0.048 0.901
22      x4 ~~      x4     1     1   22 theta.4_4.g1  .p22. 0.447  0.005 0.453
23      x5 ~~      x5     1     1   23 theta.5_5.g1  .p23. 0.486 -0.048 0.439
24      x6 ~~      x6     1     1   24 theta.6_6.g1  .p24. 0.258  0.026 0.284
25      x7 ~~      x7     1     1   25 theta.7_7.g1  .p25. 0.860 -0.007 0.853
26      x8 ~~      x8     1     1   26 theta.8_8.g1  .p26. 0.512  0.004 0.516
27      x9 ~~      x9     1     1   27 theta.9_9.g1  .p27. 0.635  0.002 0.637
28  visual ~1             1     1    0   alpha.1.g1  .p28. 0.000     NA    NA
29 textual ~1             1     1    0   alpha.2.g1  .p29. 0.000     NA    NA
30   speed ~1             1     1    0   alpha.3.g1  .p30. 0.000     NA    NA
31  visual ~~  visual     1     1    0   psi.1_1.g1  .p31. 1.000     NA    NA
32 textual ~~ textual     1     1    0   psi.2_2.g1  .p32. 1.000     NA    NA
33   speed ~~   speed     1     1    0   psi.3_3.g1  .p33. 1.000     NA    NA
34  visual ~~ textual     1     1   28   psi.2_1.g1  .p34. 0.473 -0.009 0.464
35  visual ~~   speed     1     1   29   psi.3_1.g1  .p35. 0.347 -0.007 0.341
36 textual ~~   speed     1     1   30   psi.3_2.g1  .p36. 0.320  0.001 0.320
37  visual =~      x1     2     2   31   lambda.1_1  .p37. 0.885 -0.056 0.829
38  visual =~      x2     2     2   32   lambda.2_1  .p38. 0.536  0.046 0.583
39  visual =~      x3     2     2   33   lambda.3_1  .p39. 0.707  0.033 0.740
40 textual =~      x4     2     2   34   lambda.4_2  .p40. 0.935  0.023 0.958
41 textual =~      x5     2     2   35   lambda.5_2  .p41. 1.045 -0.072 0.973
42 textual =~      x6     2     2   36   lambda.6_2  .p42. 0.874  0.065 0.939
43   speed =~      x7     2     2   37   lambda.7_3  .p43. 0.550 -0.005 0.545
44   speed =~      x8     2     2   38   lambda.8_3  .p44. 0.675  0.002 0.677
45   speed =~      x9     2     2   39   lambda.9_3  .p45. 0.602  0.002 0.604
46      x1 ~1             2     2   40      nu.1.g2  .p46. 4.930  0.000 4.930
47      x2 ~1             2     2   41      nu.2.g2  .p47. 6.198  0.000 6.198
48      x3 ~1             2     2   42      nu.3.g2  .p48. 1.992  0.000 1.992
49      x4 ~1             2     2   43      nu.4.g2  .p49. 3.318  0.000 3.318
50      x5 ~1             2     2   44      nu.5.g2  .p50. 4.714  0.000 4.714
51      x6 ~1             2     2   45      nu.6.g2  .p51. 2.467  0.000 2.467
52      x7 ~1             2     2   46      nu.7.g2  .p52. 3.923  0.000 3.923
53      x8 ~1             2     2   47      nu.8.g2  .p53. 5.488  0.000 5.488
54      x9 ~1             2     2   48      nu.9.g2  .p54. 5.338  0.000 5.338
55      x1 ~~      x1     2     2   49 theta.1_1.g2  .p55. 0.652  0.051 0.702
56      x2 ~~      x2     2     2   50 theta.2_2.g2  .p56. 0.940 -0.015 0.924
57      x3 ~~      x3     2     2   51 theta.3_3.g2  .p57. 0.606 -0.022 0.584
58      x4 ~~      x4     2     2   52 theta.4_4.g2  .p58. 0.348 -0.018 0.330
59      x5 ~~      x5     2     2   53 theta.5_5.g2  .p59. 0.371  0.050 0.421
60      x6 ~~      x6     2     2   54 theta.6_6.g2  .p60. 0.439 -0.027 0.412
61      x7 ~~      x7     2     2   55 theta.7_7.g2  .p61. 0.622  0.003 0.625
62      x8 ~~      x8     2     2   56 theta.8_8.g2  .p62. 0.410 -0.002 0.408
63      x9 ~~      x9     2     2   57 theta.9_9.g2  .p63. 0.505 -0.001 0.504
64  visual ~1             2     2    0   alpha.1.g2  .p64. 0.000     NA    NA
65 textual ~1             2     2    0   alpha.2.g2  .p65. 0.000     NA    NA
66   speed ~1             2     2    0   alpha.3.g2  .p66. 0.000     NA    NA
67  visual ~~  visual     2     2   58   psi.1_1.g2  .p67. 0.910 -0.002 0.907
68 textual ~~ textual     2     2   59   psi.2_2.g2  .p68. 1.004  0.000 1.005
69   speed ~~   speed     2     2   60   psi.3_3.g2  .p69. 1.498 -0.001 1.497
70  visual ~~ textual     2     2   61   psi.2_1.g2  .p70. 0.520  0.003 0.523
71  visual ~~   speed     2     2   62   psi.3_1.g2  .p71. 0.638  0.003 0.641
72 textual ~~   speed     2     2   63   psi.3_2.g2  .p72. 0.429  0.001 0.430
   sepc.lv sepc.all sepc.nox
1    0.072    0.062    0.062
2   -0.060   -0.048   -0.048
3   -0.052   -0.045   -0.045
4   -0.018   -0.016   -0.016
5    0.081    0.065    0.065
6   -0.042   -0.042   -0.042
7    0.013    0.012    0.012
8   -0.004   -0.004   -0.004
9   -0.004   -0.004   -0.004
10   0.000    0.000    0.000
11   0.000    0.000    0.000
12   0.000    0.000    0.000
13   0.000    0.000    0.000
14   0.000    0.000    0.000
15   0.000    0.000    0.000
16   0.000    0.000    0.000
17   0.000    0.000    0.000
18   0.000    0.000    0.000
19  -0.577   -0.424   -0.424
20   1.252    0.813    0.813
21   0.853    0.630    0.630
22   0.447    0.339    0.339
23  -0.486   -0.308   -0.308
24   0.258    0.252    0.252
25  -0.860   -0.739   -0.739
26   0.512    0.529    0.529
27   0.635    0.637    0.637
28      NA       NA       NA
29      NA       NA       NA
30      NA       NA       NA
31      NA       NA       NA
32      NA       NA       NA
33      NA       NA       NA
34  -0.009   -0.009   -0.009
35  -0.007   -0.007   -0.007
36   0.001    0.001    0.001
37  -0.053   -0.045   -0.045
38   0.044    0.040    0.040
39   0.031    0.030    0.030
40   0.023    0.021    0.021
41  -0.072   -0.060   -0.060
42   0.065    0.059    0.059
43  -0.006   -0.006   -0.006
44   0.002    0.002    0.002
45   0.003    0.003    0.003
46   0.000    0.000    0.000
47   0.000    0.000    0.000
48   0.000    0.000    0.000
49   0.000    0.000    0.000
50   0.000    0.000    0.000
51   0.000    0.000    0.000
52   0.000    0.000    0.000
53   0.000    0.000    0.000
54   0.000    0.000    0.000
55   0.652    0.478    0.478
56  -0.940   -0.782   -0.782
57  -0.606   -0.571   -0.571
58  -0.348   -0.284   -0.284
59   0.371    0.253    0.253
60  -0.439   -0.364   -0.364
61   0.622    0.578    0.578
62  -0.410   -0.375   -0.375
63  -0.505   -0.482   -0.482
64      NA       NA       NA
65      NA       NA       NA
66      NA       NA       NA
67  -1.000   -1.000   -1.000
68   1.000    1.000    1.000
69  -1.000   -1.000   -1.000
70   0.003    0.003    0.003
71   0.002    0.002    0.002
72   0.000    0.000    0.000

16.10.5.6.4 Equivalence Test

The petersenlab package (Petersen, 2024b) contains the equiv_chi() function from Counsell et al. (2020) that performs an equivalence test: https://osf.io/cqu8v. The chi-square equivalence test is non-significant, suggesting that the model fit is not acceptable.

Code

equiv_chi(
  alpha = .05,
  chi = metricInvarianceModel_chisquare,
  df = metricInvarianceModel_df,
  m = 2,
  N_sample = metricInvarianceModel_N,
  popRMSEA = .08)

Moreover, the equivalence test of the chi-square difference test is non-significant, suggesting that the degree of worsening of model fit is not acceptable. In other words, metric invariance failed.

Code

metricInvarianceModel_dfDiff <- 
  metricInvarianceModel_df - configuralInvarianceModel_df

equiv_chi(
  alpha = .05,
  chi = metricInvarianceModel_chisquareDiff,
  df = metricInvarianceModel_dfDiff,
  m = 2,
  N_sample = metricInvarianceModel_N,
  popRMSEA = .08)

16.10.5.6.5 Permutation Test

Permutation procedures for testing measurement invariance are described in (Jorgensen et al., 2018).

For reproducibility, I set the seed below. Using the same seed will yield the same answer every time. There is nothing special about this particular seed. You can specify the null model as the baseline model using: baseline.model = nullModelFit. Warning: this code takes a while to run based on \(100\) iterations. You can reduce the number of iterations to be faster.

Code

set.seed(52242)
metricInvarianceTest <- permuteMeasEq(
  nPermute = numPermutations,
  modelType = "mgcfa",
  con = metricInvarianceModel_fit,
  uncon = configuralInvarianceModel_fit,
  AFIs = myAFIs,
  moreAFIs = moreAFIs,
  parallelType = "multicore", #only 'snow' works on Windows, but right now, it is throwing an error
  iseed = 52242)

Code

RNGkind("default", "default", "default")
set.seed(52242)

metricInvarianceTest

Omnibus p value based on parametric chi-squared difference test:

Chisq diff    Df diff Pr(>Chisq) 
     5.464      6.000      0.486 


Omnibus p values based on nonparametric permutation method: 

             AFI.Difference p.value
chisq                 6.888    0.57
chisq.scaled          2.986    0.59
rmsea                -0.005    0.60
cfi                  -0.001    0.57
tli                   0.011    0.61
srmr                  0.003    0.71
rmsea.robust         -0.005    0.61
cfi.robust           -0.001    0.59
tli.robust            0.011    0.64

The p-values are non-significant, indicating that the model does not fit significantly worse than the configural invariance model. In other words, metric invariance held.

16.10.5.7 Internal Consistency Reliability

Internal consistency reliability of items composing the latent factors, as quantified by omega (\(\omega\)) and average variance extracted (AVE), was estimated using the semTools package (Jorgensen et al., 2021).

Code

compRelSEM(metricInvarianceModel_fit)

Code

AVE(metricInvarianceModel_fit)

16.10.5.8 Path Diagram

A path diagram of the model generated using the semPlot package (Epskamp, 2022) is below.

Code

semPaths(
  metricInvarianceModel_fit,
  what = "est",
  layout = "tree2",
  ask = FALSE,
  edge.label.cex = 1.2)

Figure 16.55: Metric Invariance Model in Confirmatory Factor Analysis.

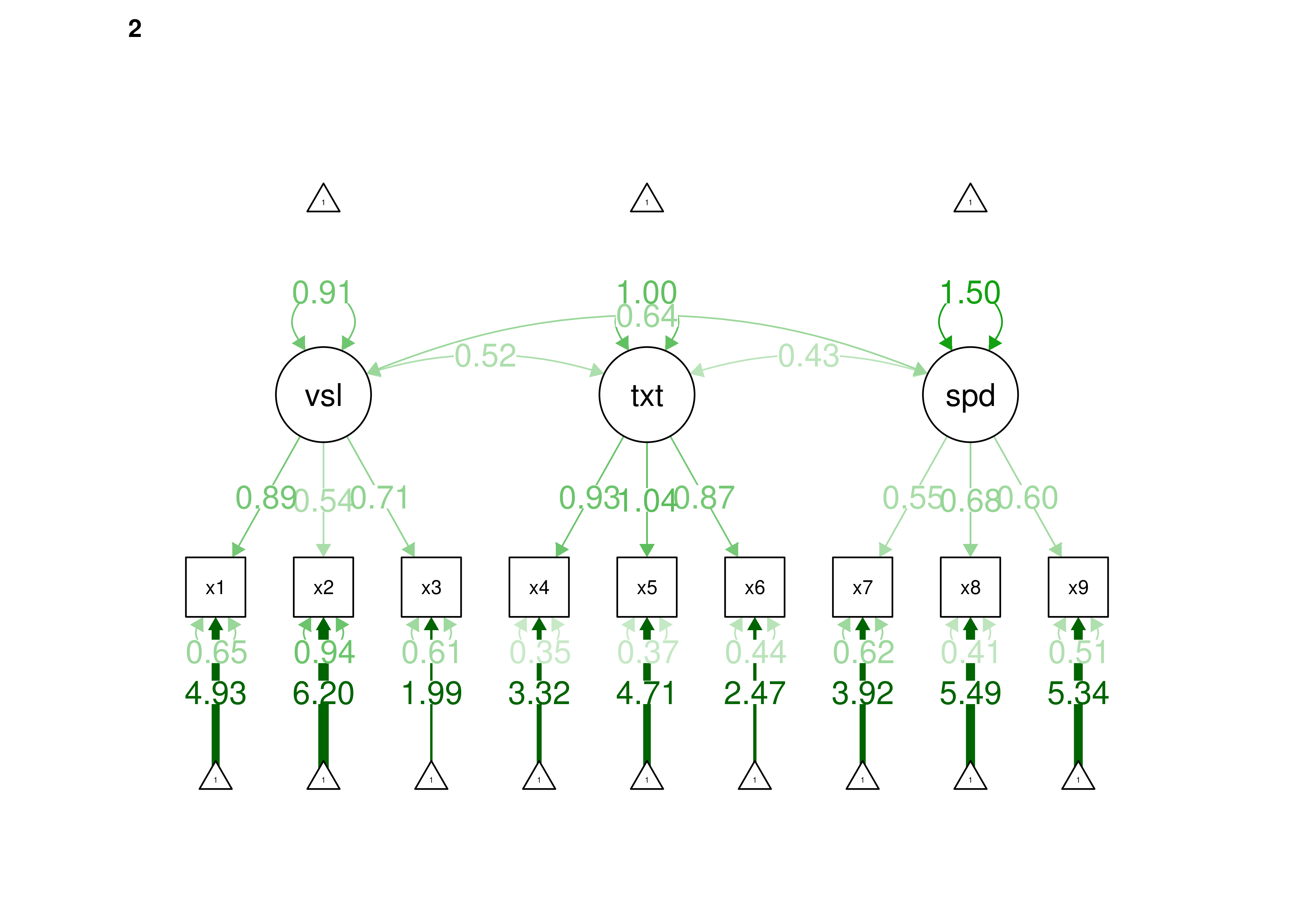
Figure 16.56: Metric Invariance Model in Confirmatory Factor Analysis.

16.10.6 Scalar (“Strong Factorial”) Invariance Model

Specify invariance of factor loadings and intercepts across groups.

16.10.6.1 Model Syntax

Code

scalarInvarianceModel <- measEq.syntax(
  configural.model = cfaModel,
  data = HolzingerSwineford1939,
  ID.fac = "std.lv",
  group = "school",
  group.equal = c("loadings","intercepts"))

Code

cat(as.character(scalarInvarianceModel))

## LOADINGS:

visual =~ c(NA, NA)*x1 + c(lambda.1_1, lambda.1_1)*x1
visual =~ c(NA, NA)*x2 + c(lambda.2_1, lambda.2_1)*x2
visual =~ c(NA, NA)*x3 + c(lambda.3_1, lambda.3_1)*x3
textual =~ c(NA, NA)*x4 + c(lambda.4_2, lambda.4_2)*x4
textual =~ c(NA, NA)*x5 + c(lambda.5_2, lambda.5_2)*x5
textual =~ c(NA, NA)*x6 + c(lambda.6_2, lambda.6_2)*x6
speed =~ c(NA, NA)*x7 + c(lambda.7_3, lambda.7_3)*x7
speed =~ c(NA, NA)*x8 + c(lambda.8_3, lambda.8_3)*x8
speed =~ c(NA, NA)*x9 + c(lambda.9_3, lambda.9_3)*x9

## INTERCEPTS:

x1 ~ c(NA, NA)*1 + c(nu.1, nu.1)*1
x2 ~ c(NA, NA)*1 + c(nu.2, nu.2)*1
x3 ~ c(NA, NA)*1 + c(nu.3, nu.3)*1
x4 ~ c(NA, NA)*1 + c(nu.4, nu.4)*1
x5 ~ c(NA, NA)*1 + c(nu.5, nu.5)*1
x6 ~ c(NA, NA)*1 + c(nu.6, nu.6)*1
x7 ~ c(NA, NA)*1 + c(nu.7, nu.7)*1
x8 ~ c(NA, NA)*1 + c(nu.8, nu.8)*1
x9 ~ c(NA, NA)*1 + c(nu.9, nu.9)*1

## UNIQUE-FACTOR VARIANCES:

x1 ~~ c(NA, NA)*x1 + c(theta.1_1.g1, theta.1_1.g2)*x1
x2 ~~ c(NA, NA)*x2 + c(theta.2_2.g1, theta.2_2.g2)*x2
x3 ~~ c(NA, NA)*x3 + c(theta.3_3.g1, theta.3_3.g2)*x3
x4 ~~ c(NA, NA)*x4 + c(theta.4_4.g1, theta.4_4.g2)*x4
x5 ~~ c(NA, NA)*x5 + c(theta.5_5.g1, theta.5_5.g2)*x5
x6 ~~ c(NA, NA)*x6 + c(theta.6_6.g1, theta.6_6.g2)*x6
x7 ~~ c(NA, NA)*x7 + c(theta.7_7.g1, theta.7_7.g2)*x7
x8 ~~ c(NA, NA)*x8 + c(theta.8_8.g1, theta.8_8.g2)*x8
x9 ~~ c(NA, NA)*x9 + c(theta.9_9.g1, theta.9_9.g2)*x9

## LATENT MEANS/INTERCEPTS:

visual ~ c(0, NA)*1 + c(alpha.1.g1, alpha.1.g2)*1
textual ~ c(0, NA)*1 + c(alpha.2.g1, alpha.2.g2)*1
speed ~ c(0, NA)*1 + c(alpha.3.g1, alpha.3.g2)*1

## COMMON-FACTOR VARIANCES:

visual ~~ c(1, NA)*visual + c(psi.1_1.g1, psi.1_1.g2)*visual
textual ~~ c(1, NA)*textual + c(psi.2_2.g1, psi.2_2.g2)*textual
speed ~~ c(1, NA)*speed + c(psi.3_3.g1, psi.3_3.g2)*speed

## COMMON-FACTOR COVARIANCES:

visual ~~ c(NA, NA)*textual + c(psi.2_1.g1, psi.2_1.g2)*textual
visual ~~ c(NA, NA)*speed + c(psi.3_1.g1, psi.3_1.g2)*speed
textual ~~ c(NA, NA)*speed + c(psi.3_2.g1, psi.3_2.g2)*speed

Code

scalarInvarianceSyntax <- as.character(scalarInvarianceModel)

16.10.6.1.1 Summary of Model Features

Code

summary(scalarInvarianceModel)

This lavaan model syntax specifies a CFA with 9 manifest indicators of 3 common factor(s).

To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed.

Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor:

   visual textual speed
x1 num                 
x2 num                 
x3 num                 
x4        num          
x5        num          
x6        num          
x7                num  
x8                num  
x9                num  

The following types of parameter were constrained to equality across groups:

    loadings
    intercepts

16.10.6.2 Model Syntax in Table Form

Code

lavaanify(scalarInvarianceModel, ngroups = 2)

Code

lavaanify(cfaModel_scalarInvariance, ngroups = 2)

16.10.6.3 Fit the Model

Code

scalarInvarianceModel_fit <- cfa(
  scalarInvarianceSyntax,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

Code

scalarInvarianceModelFullSyntax_fit <- lavaan(
  cfaModel_scalarInvariance,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

16.10.6.4 Model Summary

Code

summary(
  scalarInvarianceModel_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 66 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        66
  Number of equality constraints                    18

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               156.955     159.442
  Degrees of freedom                                60          60
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.984
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     86.521      86.521
    Grant-White                                 72.921      72.921

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.887       0.881
  Tucker-Lewis Index (TLI)                       0.865       0.857
                                                                  
  Robust Comparative Fit Index (CFI)                         0.890
  Robust Tucker-Lewis Index (TLI)                            0.868

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3672.597   -3672.597
  Scaling correction factor                                  0.797
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7441.195    7441.195
  Bayesian (BIC)                              7619.136    7619.136
  Sample-size adjusted Bayesian (SABIC)       7466.908    7466.908

Root Mean Square Error of Approximation:

  RMSEA                                          0.104       0.105
  90 Percent confidence interval - lower         0.084       0.085
  90 Percent confidence interval - upper         0.124       0.125
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    0.975       0.980
                                                                  
  Robust RMSEA                                               0.104
  90 Percent confidence interval - lower                     0.083
  90 Percent confidence interval - upper                     0.124
  P-value H_0: Robust RMSEA <= 0.050                         0.000
  P-value H_0: Robust RMSEA >= 0.080                         0.972

Standardized Root Mean Square Residual:

  SRMR                                           0.080       0.080

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.874    0.132    6.630    0.000    0.874    0.751
    x2      (l.2_)    0.512    0.086    5.984    0.000    0.512    0.411
    x3      (l.3_)    0.722    0.095    7.610    0.000    0.722    0.604
  textual =~                                                            
    x4      (l.4_)    0.921    0.071   12.920    0.000    0.921    0.807
    x5      (l.5_)    1.059    0.077   13.763    0.000    1.059    0.837
    x6      (l.6_)    0.875    0.066   13.259    0.000    0.875    0.865
  speed =~                                                              
    x7      (l.7_)    0.566    0.081    6.946    0.000    0.566    0.512
    x8      (l.8_)    0.657    0.082    8.028    0.000    0.657    0.669
    x9      (l.9_)    0.602    0.085    7.049    0.000    0.602    0.604

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.473    0.108    4.397    0.000    0.473    0.473
    speed  (p.3_1)    0.355    0.125    2.842    0.004    0.355    0.355
  textual ~~                                                            
    speed  (p.3_2)    0.322    0.095    3.377    0.001    0.322    0.322

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (nu.1)    5.016    0.094   53.146    0.000    5.016    4.309
   .x2      (nu.2)    6.156    0.088   69.594    0.000    6.156    4.944
   .x3      (nu.3)    2.292    0.098   23.329    0.000    2.292    1.916
   .x4      (nu.4)    2.780    0.086   32.469    0.000    2.780    2.435
   .x5      (nu.5)    4.035    0.104   38.981    0.000    4.035    3.189
   .x6      (nu.6)    1.928    0.074   25.882    0.000    1.928    1.907
   .x7      (nu.7)    4.244    0.078   54.164    0.000    4.244    3.840
   .x8      (nu.8)    5.627    0.076   73.915    0.000    5.627    5.726
   .x9      (nu.9)    5.474    0.073   74.934    0.000    5.474    5.492
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.591    0.179    3.295    0.001    0.591    0.436
   .x2      (t.2_)    1.288    0.160    8.075    0.000    1.288    0.831
   .x3      (t.3_)    0.910    0.151    6.046    0.000    0.910    0.636
   .x4      (t.4_)    0.454    0.073    6.245    0.000    0.454    0.349
   .x5      (t.5_)    0.480    0.076    6.295    0.000    0.480    0.300
   .x6      (t.6_)    0.257    0.058    4.401    0.000    0.257    0.252
   .x7      (t.7_)    0.901    0.129    7.000    0.000    0.901    0.738
   .x8      (t.8_)    0.534    0.091    5.838    0.000    0.534    0.553
   .x9      (t.9_)    0.631    0.115    5.469    0.000    0.631    0.635
    visual  (p.1_)    1.000                               1.000    1.000
    textual (p.2_)    1.000                               1.000    1.000
    speed   (p.3_)    1.000                               1.000    1.000

R-Square:
                   Estimate
    x1                0.564
    x2                0.169
    x3                0.364
    x4                0.651
    x5                0.700
    x6                0.748
    x7                0.262
    x8                0.447
    x9                0.365


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.874    0.132    6.630    0.000    0.827    0.711
    x2      (l.2_)    0.512    0.086    5.984    0.000    0.485    0.441
    x3      (l.3_)    0.722    0.095    7.610    0.000    0.684    0.649
  textual =~                                                            
    x4      (l.4_)    0.921    0.071   12.920    0.000    0.921    0.838
    x5      (l.5_)    1.059    0.077   13.763    0.000    1.059    0.869
    x6      (l.6_)    0.875    0.066   13.259    0.000    0.875    0.797
  speed =~                                                              
    x7      (l.7_)    0.566    0.081    6.946    0.000    0.692    0.651
    x8      (l.8_)    0.657    0.082    8.028    0.000    0.803    0.773
    x9      (l.9_)    0.602    0.085    7.049    0.000    0.736    0.722

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.519    0.136    3.829    0.000    0.549    0.549
    speed  (p.3_1)    0.649    0.215    3.014    0.003    0.561    0.561
  textual ~~                                                            
    speed  (p.3_2)    0.442    0.189    2.335    0.020    0.361    0.361

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (nu.1)    5.016    0.094   53.146    0.000    5.016    4.312
   .x2      (nu.2)    6.156    0.088   69.594    0.000    6.156    5.602
   .x3      (nu.3)    2.292    0.098   23.329    0.000    2.292    2.177
   .x4      (nu.4)    2.780    0.086   32.469    0.000    2.780    2.529
   .x5      (nu.5)    4.035    0.104   38.981    0.000    4.035    3.312
   .x6      (nu.6)    1.928    0.074   25.882    0.000    1.928    1.756
   .x7      (nu.7)    4.244    0.078   54.164    0.000    4.244    3.990
   .x8      (nu.8)    5.627    0.076   73.915    0.000    5.627    5.412
   .x9      (nu.9)    5.474    0.073   74.934    0.000    5.474    5.370
    visual  (a.1.)   -0.193    0.175   -1.101    0.271   -0.204   -0.204
    textual (a.2.)    0.617    0.135    4.587    0.000    0.617    0.617
    speed   (a.3.)   -0.294    0.161   -1.828    0.068   -0.240   -0.240

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.668    0.176    3.793    0.000    0.668    0.494
   .x2      (t.2_)    0.973    0.152    6.384    0.000    0.973    0.805
   .x3      (t.3_)    0.641    0.133    4.833    0.000    0.641    0.578
   .x4      (t.4_)    0.359    0.066    5.464    0.000    0.359    0.297
   .x5      (t.5_)    0.363    0.074    4.883    0.000    0.363    0.245
   .x6      (t.6_)    0.441    0.075    5.851    0.000    0.441    0.366
   .x7      (t.7_)    0.652    0.108    6.016    0.000    0.652    0.577
   .x8      (t.8_)    0.436    0.152    2.872    0.004    0.436    0.403
   .x9      (t.9_)    0.497    0.127    3.918    0.000    0.497    0.478
    visual  (p.1_)    0.896    0.235    3.816    0.000    1.000    1.000
    textual (p.2_)    1.000    0.194    5.157    0.000    1.000    1.000
    speed   (p.3_)    1.495    0.360    4.156    0.000    1.000    1.000

R-Square:
                   Estimate
    x1                0.506
    x2                0.195
    x3                0.422
    x4                0.703
    x5                0.755
    x6                0.634
    x7                0.423
    x8                0.597
    x9                0.522

Code

summary(
  scalarInvarianceModelFullSyntax_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 66 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        66
  Number of equality constraints                    18

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               156.955     159.442
  Degrees of freedom                                60          60
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.984
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     86.520      86.520
    Grant-White                                 72.921      72.921

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.887       0.881
  Tucker-Lewis Index (TLI)                       0.865       0.857
                                                                  
  Robust Comparative Fit Index (CFI)                         0.890
  Robust Tucker-Lewis Index (TLI)                            0.868

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3672.597   -3672.597
  Scaling correction factor                                  0.797
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7441.195    7441.195
  Bayesian (BIC)                              7619.136    7619.136
  Sample-size adjusted Bayesian (SABIC)       7466.908    7466.908

Root Mean Square Error of Approximation:

  RMSEA                                          0.104       0.105
  90 Percent confidence interval - lower         0.084       0.085
  90 Percent confidence interval - upper         0.124       0.125
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    0.975       0.980
                                                                  
  Robust RMSEA                                               0.104
  90 Percent confidence interval - lower                     0.083
  90 Percent confidence interval - upper                     0.124
  P-value H_0: Robust RMSEA <= 0.050                         0.000
  P-value H_0: Robust RMSEA >= 0.080                         0.972

Standardized Root Mean Square Residual:

  SRMR                                           0.080       0.080

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.874    0.132    6.630    0.000    0.874    0.751
    x2      (lmb2)    0.512    0.086    5.984    0.000    0.512    0.411
    x3      (lmb3)    0.722    0.095    7.610    0.000    0.722    0.604
  textual =~                                                            
    x4      (lmb4)    0.921    0.071   12.920    0.000    0.921    0.807
    x5      (lmb5)    1.059    0.077   13.763    0.000    1.059    0.837
    x6      (lmb6)    0.875    0.066   13.259    0.000    0.875    0.865
  speed =~                                                              
    x7      (lmb7)    0.566    0.081    6.946    0.000    0.566    0.512
    x8      (lmb8)    0.657    0.082    8.028    0.000    0.657    0.669
    x9      (lmb9)    0.602    0.085    7.049    0.000    0.602    0.604

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.473    0.108    4.397    0.000    0.473    0.473
    speed             0.355    0.125    2.842    0.004    0.355    0.355
  textual ~~                                                            
    speed             0.322    0.095    3.377    0.001    0.322    0.322

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1      (int1)    5.016    0.094   53.146    0.000    5.016    4.309
   .x2      (int2)    6.156    0.088   69.594    0.000    6.156    4.944
   .x3      (int3)    2.292    0.098   23.329    0.000    2.292    1.916
   .x4      (int4)    2.780    0.086   32.469    0.000    2.780    2.435
   .x5      (int5)    4.035    0.104   38.981    0.000    4.035    3.189
   .x6      (int6)    1.928    0.074   25.882    0.000    1.928    1.907
   .x7      (int7)    4.244    0.078   54.164    0.000    4.244    3.840
   .x8      (int8)    5.627    0.076   73.915    0.000    5.627    5.726
   .x9      (int9)    5.474    0.073   74.934    0.000    5.474    5.492

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            1.000                               1.000    1.000
    textual           1.000                               1.000    1.000
    speed             1.000                               1.000    1.000
   .x1                0.591    0.179    3.295    0.001    0.591    0.436
   .x2                1.288    0.160    8.075    0.000    1.288    0.831
   .x3                0.910    0.151    6.046    0.000    0.910    0.636
   .x4                0.454    0.073    6.245    0.000    0.454    0.349
   .x5                0.480    0.076    6.295    0.000    0.480    0.300
   .x6                0.257    0.058    4.401    0.000    0.257    0.252
   .x7                0.901    0.129    7.000    0.000    0.901    0.738
   .x8                0.534    0.091    5.838    0.000    0.534    0.553
   .x9                0.631    0.115    5.469    0.000    0.631    0.635

R-Square:
                   Estimate
    x1                0.564
    x2                0.169
    x3                0.364
    x4                0.651
    x5                0.700
    x6                0.748
    x7                0.262
    x8                0.447
    x9                0.365


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.874    0.132    6.630    0.000    0.827    0.711
    x2      (lmb2)    0.512    0.086    5.984    0.000    0.485    0.441
    x3      (lmb3)    0.722    0.095    7.610    0.000    0.684    0.649
  textual =~                                                            
    x4      (lmb4)    0.921    0.071   12.920    0.000    0.921    0.838
    x5      (lmb5)    1.059    0.077   13.763    0.000    1.059    0.869
    x6      (lmb6)    0.875    0.066   13.259    0.000    0.875    0.797
  speed =~                                                              
    x7      (lmb7)    0.566    0.081    6.946    0.000    0.692    0.651
    x8      (lmb8)    0.657    0.082    8.028    0.000    0.803    0.773
    x9      (lmb9)    0.602    0.085    7.049    0.000    0.736    0.722

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.519    0.136    3.829    0.000    0.549    0.549
    speed             0.649    0.215    3.014    0.003    0.561    0.561
  textual ~~                                                            
    speed             0.442    0.189    2.335    0.020    0.361    0.361

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual           -0.193    0.175   -1.101    0.271   -0.204   -0.204
    textual           0.617    0.135    4.587    0.000    0.617    0.617
    speed            -0.294    0.161   -1.828    0.068   -0.240   -0.240
   .x1      (int1)    5.016    0.094   53.146    0.000    5.016    4.312
   .x2      (int2)    6.156    0.088   69.594    0.000    6.156    5.602
   .x3      (int3)    2.292    0.098   23.329    0.000    2.292    2.177
   .x4      (int4)    2.780    0.086   32.469    0.000    2.780    2.529
   .x5      (int5)    4.035    0.104   38.981    0.000    4.035    3.312
   .x6      (int6)    1.928    0.074   25.882    0.000    1.928    1.756
   .x7      (int7)    4.244    0.078   54.164    0.000    4.244    3.990
   .x8      (int8)    5.627    0.076   73.915    0.000    5.627    5.412
   .x9      (int9)    5.474    0.073   74.934    0.000    5.474    5.370

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.896    0.235    3.815    0.000    1.000    1.000
    textual           1.000    0.194    5.157    0.000    1.000    1.000
    speed             1.495    0.360    4.156    0.000    1.000    1.000
   .x1                0.668    0.176    3.793    0.000    0.668    0.494
   .x2                0.973    0.152    6.384    0.000    0.973    0.805
   .x3                0.641    0.133    4.833    0.000    0.641    0.578
   .x4                0.359    0.066    5.464    0.000    0.359    0.297
   .x5                0.363    0.074    4.883    0.000    0.363    0.245
   .x6                0.441    0.075    5.851    0.000    0.441    0.366
   .x7                0.652    0.108    6.016    0.000    0.652    0.577
   .x8                0.436    0.152    2.872    0.004    0.436    0.403
   .x9                0.497    0.127    3.918    0.000    0.497    0.478

R-Square:
                   Estimate
    x1                0.506
    x2                0.195
    x3                0.422
    x4                0.703
    x5                0.755
    x6                0.634
    x7                0.423
    x8                0.597
    x9                0.522

16.10.6.5 Model Fit

You can specify the null model as the baseline model using: baseline.model = nullModelFit

Code

fitMeasures(scalarInvarianceModel_fit)

                         npar                          fmin 
                       48.000                         0.261 
                        chisq                            df 
                      156.955                        60.000 
                       pvalue                  chisq.scaled 
                        0.000                       159.442 
                    df.scaled                 pvalue.scaled 
                       60.000                         0.000 
         chisq.scaling.factor                baseline.chisq 
                        0.984                       932.665 
                  baseline.df               baseline.pvalue 
                       72.000                         0.000 
        baseline.chisq.scaled            baseline.df.scaled 
                      909.019                        72.000 
       baseline.pvalue.scaled baseline.chisq.scaling.factor 
                        0.000                         1.026 
                          cfi                           tli 
                        0.887                         0.865 
                   cfi.scaled                    tli.scaled 
                        0.881                         0.857 
                   cfi.robust                    tli.robust 
                        0.890                         0.868 
                         nnfi                           rfi 
                        0.865                         0.798 
                          nfi                          pnfi 
                        0.832                         0.693 
                          ifi                           rni 
                        0.889                         0.887 
                  nnfi.scaled                    rfi.scaled 
                        0.857                         0.790 
                   nfi.scaled                   pnfi.scaled 
                        0.825                         0.687 
                   ifi.scaled                    rni.scaled 
                        0.883                         0.881 
                  nnfi.robust                    rni.robust 
                        0.868                         0.890 
                         logl             unrestricted.logl 
                    -3672.597                     -3594.120 
                          aic                           bic 
                     7441.195                      7619.136 
                       ntotal                          bic2 
                      301.000                      7466.908 
            scaling.factor.h1             scaling.factor.h0 
                        1.034                         0.797 
                        rmsea                rmsea.ci.lower 
                        0.104                         0.084 
               rmsea.ci.upper                rmsea.ci.level 
                        0.124                         0.900 
                 rmsea.pvalue                rmsea.close.h0 
                        0.000                         0.050 
        rmsea.notclose.pvalue             rmsea.notclose.h0 
                        0.975                         0.080 
                 rmsea.scaled         rmsea.ci.lower.scaled 
                        0.105                         0.085 
        rmsea.ci.upper.scaled           rmsea.pvalue.scaled 
                        0.125                         0.000 
 rmsea.notclose.pvalue.scaled                  rmsea.robust 
                        0.980                         0.104 
        rmsea.ci.lower.robust         rmsea.ci.upper.robust 
                        0.083                         0.124 
          rmsea.pvalue.robust  rmsea.notclose.pvalue.robust 
                        0.000                         0.972 
                          rmr                    rmr_nomean 
                        0.097                         0.095 
                         srmr                  srmr_bentler 
                        0.080                         0.080 
          srmr_bentler_nomean                          crmr 
                        0.076                         0.084 
                  crmr_nomean                    srmr_mplus 
                        0.081                         0.084 
            srmr_mplus_nomean                         cn_05 
                        0.075                       152.660 
                        cn_01                           gfi 
                      170.490                         0.993 
                         agfi                          pgfi 
                        0.987                         0.552 
                          mfi                          ecvi 
                        0.851                         0.840 

Code

scalarInvarianceModelFitIndices <- fitMeasures(
  scalarInvarianceModel_fit)[c(
    "cfi.robust", "rmsea.robust", "srmr")]

scalarInvarianceModel_chisquare <- fitMeasures(
  scalarInvarianceModel_fit)[c("chisq.scaled")]

scalarInvarianceModel_chisquareScaling <- fitMeasures(
  scalarInvarianceModel_fit)[c("chisq.scaling.factor")]

scalarInvarianceModel_df <- fitMeasures(
  scalarInvarianceModel_fit)[c("df.scaled")]

scalarInvarianceModel_N <- lavInspect(
  scalarInvarianceModel_fit, what = "ntotal")

16.10.6.6 Compare Model Fit

16.10.6.6.1 Nested Model (\(\chi^2\)) Difference Test

The metric invariance model and the scalar (“strong factorial”) invariance model are considered “nested” models. The scalar invariance model is nested within the metric invariance model because the metric invariance model includes all of the terms of the metric invariance model along with additional terms. Model fit of nested models can be compared with a chi-square difference test, also known as a likelihood ratio test or deviance test. A significant chi-square difference test would indicate that the simplified model with additional constraints (the scalar invariance model) is significantly worse fitting than the more complex model that has fewer constraints (the metric invariance model).

Code

anova(metricInvarianceModel_fit, scalarInvarianceModel_fit)

The scalar invariance model fit significantly worse than the configural invariance model, so scalar invariance did not hold. This provides evidence of measurement non-invariance of indicator intercepts across groups. Measurement non-invariance of indicator intercepts poses challenges to being able to meaningfully compare levels on the latent factor across groups (Little et al., 2007).

The petersenlab package (Petersen, 2024b) contains the satorraBentlerScaledChiSquareDifferenceTestStatistic() function that performs a Satorra-Bentler scaled chi-square difference test:

Code

scalarInvarianceModel_chisquareDiff <- 
  satorraBentlerScaledChiSquareDifferenceTestStatistic(
    T0 = scalarInvarianceModel_chisquare,
    c0 = scalarInvarianceModel_chisquareScaling,
    d0 = scalarInvarianceModel_df,
    T1 = metricInvarianceModel_chisquare,
    c1 = metricInvarianceModel_chisquareScaling,
    d1 = metricInvarianceModel_df)

scalarInvarianceModel_chisquareDiff

chisq.scaled 
      41.928 

16.10.6.6.2 Compare Other Fit Criteria

Code

round(
  scalarInvarianceModelFitIndices - metricInvarianceModelFitIndices,
  digits = 3)

  cfi.robust rmsea.robust         srmr 
      -0.038        0.015        0.011 

16.10.6.6.3 Score-Based Test

Score-based tests of measurement invariance are implemented using the strucchange package and are described by T. Wang et al. (2014).

Code

coef(scalarInvarianceModel_fit)

  lambda.1_1   lambda.2_1   lambda.3_1   lambda.4_2   lambda.5_2   lambda.6_2 
       0.874        0.512        0.722        0.921        1.059        0.875 
  lambda.7_3   lambda.8_3   lambda.9_3         nu.1         nu.2         nu.3 
       0.566        0.657        0.602        5.016        6.156        2.292 
        nu.4         nu.5         nu.6         nu.7         nu.8         nu.9 
       2.780        4.035        1.928        4.244        5.627        5.474 
theta.1_1.g1 theta.2_2.g1 theta.3_3.g1 theta.4_4.g1 theta.5_5.g1 theta.6_6.g1 
       0.591        1.288        0.910        0.454        0.480        0.257 
theta.7_7.g1 theta.8_8.g1 theta.9_9.g1   psi.2_1.g1   psi.3_1.g1   psi.3_2.g1 
       0.901        0.534        0.631        0.473        0.355        0.322 
  lambda.1_1   lambda.2_1   lambda.3_1   lambda.4_2   lambda.5_2   lambda.6_2 
       0.874        0.512        0.722        0.921        1.059        0.875 
  lambda.7_3   lambda.8_3   lambda.9_3         nu.1         nu.2         nu.3 
       0.566        0.657        0.602        5.016        6.156        2.292 
        nu.4         nu.5         nu.6         nu.7         nu.8         nu.9 
       2.780        4.035        1.928        4.244        5.627        5.474 
theta.1_1.g2 theta.2_2.g2 theta.3_3.g2 theta.4_4.g2 theta.5_5.g2 theta.6_6.g2 
       0.668        0.973        0.641        0.359        0.363        0.441 
theta.7_7.g2 theta.8_8.g2 theta.9_9.g2   alpha.1.g2   alpha.2.g2   alpha.3.g2 
       0.652        0.436        0.497       -0.193        0.617       -0.294 
  psi.1_1.g2   psi.2_2.g2   psi.3_3.g2   psi.2_1.g2   psi.3_1.g2   psi.3_2.g2 
       0.896        1.000        1.495        0.519        0.649        0.442 

Code

coef(scalarInvarianceModel_fit)[10:18]

    nu.1     nu.2     nu.3     nu.4     nu.5     nu.6     nu.7     nu.8 
5.015537 6.155701 2.292365 2.779781 4.034564 1.928163 4.243593 5.626570 
    nu.9 
5.474024 

Code

strucchange::sctest(
  scalarInvarianceModel_fit,
  order.by = HolzingerSwineford1939$school,
  parm = 10:18,
  functional = "LMuo")

    M-fluctuation test

data:  scalarInvarianceModel_fit
f(efp) = 44.639, p-value = 1.076e-06

A score-based test and expected parameter change (EPC) estimates (Oberski, 2014; Oberski et al., 2015) are provided by the lavaan package (Rosseel et al., 2022).

Code

lavTestScore(
  scalarInvarianceModel_fit,
  epc = TRUE
)

$test

total score test:

   test     X2 df p.value
1 score 46.446 18       0

$uni

univariate score tests:

     lhs op   rhs     X2 df p.value
1   .p1. == .p37.  2.216  1   0.137
2   .p2. == .p38.  0.115  1   0.734
3   .p3. == .p39.  1.483  1   0.223
4   .p4. == .p40.  0.039  1   0.843
5   .p5. == .p41.  2.724  1   0.099
6   .p6. == .p42.  2.205  1   0.138
7   .p7. == .p43.  0.088  1   0.767
8   .p8. == .p44.  0.035  1   0.851
9   .p9. == .p45.  0.010  1   0.922
10 .p10. == .p46.  6.336  1   0.012
11 .p11. == .p47.  7.421  1   0.006
12 .p12. == .p48. 20.450  1   0.000
13 .p13. == .p49.  1.216  1   0.270
14 .p14. == .p50.  1.146  1   0.284
15 .p15. == .p51.  0.001  1   0.976
16 .p16. == .p52. 15.301  1   0.000
17 .p17. == .p53.  4.102  1   0.043
18 .p18. == .p54.  1.602  1   0.206

$epc

expected parameter changes (epc) and expected parameter values (epv):

       lhs op     rhs block group free        label plabel    est    epc    epv
1   visual =~      x1     1     1    1   lambda.1_1   .p1.  0.874  0.100  0.974
2   visual =~      x2     1     1    2   lambda.2_1   .p2.  0.512 -0.038  0.474
3   visual =~      x3     1     1    3   lambda.3_1   .p3.  0.722 -0.098  0.624
4  textual =~      x4     1     1    4   lambda.4_2   .p4.  0.921 -0.006  0.915
5  textual =~      x5     1     1    5   lambda.5_2   .p5.  1.059  0.067  1.126
6  textual =~      x6     1     1    6   lambda.6_2   .p6.  0.875 -0.042  0.833
7    speed =~      x7     1     1    7   lambda.7_3   .p7.  0.566 -0.024  0.542
8    speed =~      x8     1     1    8   lambda.8_3   .p8.  0.657  0.012  0.669
9    speed =~      x9     1     1    9   lambda.9_3   .p9.  0.602  0.004  0.606
10      x1 ~1             1     1   10         nu.1  .p10.  5.016 -0.068  4.948
11      x2 ~1             1     1   11         nu.2  .p11.  6.156 -0.172  5.984
12      x3 ~1             1     1   12         nu.3  .p12.  2.292  0.217  2.510
13      x4 ~1             1     1   13         nu.4  .p13.  2.780  0.034  2.814
14      x5 ~1             1     1   14         nu.5  .p14.  4.035 -0.032  4.002
15      x6 ~1             1     1   15         nu.6  .p15.  1.928  0.001  1.929
16      x7 ~1             1     1   16         nu.7  .p16.  4.244  0.195  4.439
17      x8 ~1             1     1   17         nu.8  .p17.  5.627 -0.063  5.563
18      x9 ~1             1     1   18         nu.9  .p18.  5.474 -0.048  5.426
19      x1 ~~      x1     1     1   19 theta.1_1.g1  .p19.  0.591 -0.132  0.459
20      x2 ~~      x2     1     1   20 theta.2_2.g1  .p20.  1.288  0.022  1.310
21      x3 ~~      x3     1     1   21 theta.3_3.g1  .p21.  0.910  0.086  0.997
22      x4 ~~      x4     1     1   22 theta.4_4.g1  .p22.  0.454  0.000  0.454
23      x5 ~~      x5     1     1   23 theta.5_5.g1  .p23.  0.480 -0.042  0.437
24      x6 ~~      x6     1     1   24 theta.6_6.g1  .p24.  0.257  0.026  0.283
25      x7 ~~      x7     1     1   25 theta.7_7.g1  .p25.  0.901  0.013  0.914
26      x8 ~~      x8     1     1   26 theta.8_8.g1  .p26.  0.534 -0.010  0.524
27      x9 ~~      x9     1     1   27 theta.9_9.g1  .p27.  0.631 -0.002  0.629
28  visual ~1             1     1    0   alpha.1.g1  .p28.  0.000     NA     NA
29 textual ~1             1     1    0   alpha.2.g1  .p29.  0.000     NA     NA
30   speed ~1             1     1    0   alpha.3.g1  .p30.  0.000     NA     NA
31  visual ~~  visual     1     1    0   psi.1_1.g1  .p31.  1.000     NA     NA
32 textual ~~ textual     1     1    0   psi.2_2.g1  .p32.  1.000     NA     NA
33   speed ~~   speed     1     1    0   psi.3_3.g1  .p33.  1.000     NA     NA
34  visual ~~ textual     1     1   28   psi.2_1.g1  .p34.  0.473 -0.013  0.460
35  visual ~~   speed     1     1   29   psi.3_1.g1  .p35.  0.355 -0.010  0.345
36 textual ~~   speed     1     1   30   psi.3_2.g1  .p36.  0.322  0.000  0.322
37  visual =~      x1     2     2   31   lambda.1_1  .p37.  0.874 -0.035  0.839
38  visual =~      x2     2     2   32   lambda.2_1  .p38.  0.512  0.068  0.580
39  visual =~      x3     2     2   33   lambda.3_1  .p39.  0.722 -0.002  0.721
40 textual =~      x4     2     2   34   lambda.4_2  .p40.  0.921  0.038  0.959
41 textual =~      x5     2     2   35   lambda.5_2  .p41.  1.059 -0.086  0.973
42 textual =~      x6     2     2   36   lambda.6_2  .p42.  0.875  0.067  0.942
43   speed =~      x7     2     2   37   lambda.7_3  .p43.  0.566 -0.036  0.530
44   speed =~      x8     2     2   38   lambda.8_3  .p44.  0.657  0.017  0.674
45   speed =~      x9     2     2   39   lambda.9_3  .p45.  0.602  0.009  0.611
46      x1 ~1             2     2   40         nu.1  .p46.  5.016  0.066  5.081
47      x2 ~1             2     2   41         nu.2  .p47.  6.156  0.148  6.304
48      x3 ~1             2     2   42         nu.3  .p48.  2.292 -0.169  2.123
49      x4 ~1             2     2   43         nu.4  .p49.  2.780 -0.053  2.727
50      x5 ~1             2     2   44         nu.5  .p50.  4.035  0.080  4.115
51      x6 ~1             2     2   45         nu.6  .p51.  1.928 -0.042  1.886
52      x7 ~1             2     2   46         nu.7  .p52.  4.244 -0.158  4.086
53      x8 ~1             2     2   47         nu.8  .p53.  5.627  0.068  5.695
54      x9 ~1             2     2   48         nu.9  .p54.  5.474  0.051  5.525
55      x1 ~~      x1     2     2   49 theta.1_1.g2  .p55.  0.668  0.029  0.697
56      x2 ~~      x2     2     2   50 theta.2_2.g2  .p56.  0.973 -0.021  0.952
57      x3 ~~      x3     2     2   51 theta.3_3.g2  .p57.  0.641 -0.002  0.639
58      x4 ~~      x4     2     2   52 theta.4_4.g2  .p58.  0.359 -0.026  0.333
59      x5 ~~      x5     2     2   53 theta.5_5.g2  .p59.  0.363  0.064  0.427
60      x6 ~~      x6     2     2   54 theta.6_6.g2  .p60.  0.441 -0.029  0.411
61      x7 ~~      x7     2     2   55 theta.7_7.g2  .p61.  0.652  0.021  0.674
62      x8 ~~      x8     2     2   56 theta.8_8.g2  .p62.  0.436 -0.015  0.420
63      x9 ~~      x9     2     2   57 theta.9_9.g2  .p63.  0.497 -0.004  0.493
64  visual ~1             2     2   58   alpha.1.g2  .p64. -0.193  0.011 -0.182
65 textual ~1             2     2   59   alpha.2.g2  .p65.  0.617 -0.001  0.617
66   speed ~1             2     2   60   alpha.3.g2  .p66. -0.294 -0.013 -0.307
67  visual ~~  visual     2     2   61   psi.1_1.g2  .p67.  0.896  0.001  0.897
68 textual ~~ textual     2     2   62   psi.2_2.g2  .p68.  1.000  0.001  1.000
69   speed ~~   speed     2     2   63   psi.3_3.g2  .p69.  1.495 -0.003  1.492
70  visual ~~ textual     2     2   64   psi.2_1.g2  .p70.  0.519  0.004  0.524
71  visual ~~   speed     2     2   65   psi.3_1.g2  .p71.  0.649  0.002  0.650
72 textual ~~   speed     2     2   66   psi.3_2.g2  .p72.  0.442  0.000  0.442
   sepc.lv sepc.all sepc.nox
1    0.100    0.086    0.086
2   -0.038   -0.031   -0.031
3   -0.098   -0.082   -0.082
4   -0.006   -0.005   -0.005
5    0.067    0.053    0.053
6   -0.042   -0.042   -0.042
7   -0.024   -0.021   -0.021
8    0.012    0.012    0.012
9    0.004    0.004    0.004
10  -0.068   -0.058   -0.058
11  -0.172   -0.138   -0.138
12   0.217    0.182    0.182
13   0.034    0.030    0.030
14  -0.032   -0.026   -0.026
15   0.001    0.001    0.001
16   0.195    0.177    0.177
17  -0.063   -0.064   -0.064
18  -0.048   -0.048   -0.048
19  -0.591   -0.436   -0.436
20   1.288    0.831    0.831
21   0.910    0.636    0.636
22   0.454    0.349    0.349
23  -0.480   -0.300   -0.300
24   0.257    0.252    0.252
25   0.901    0.738    0.738
26  -0.534   -0.553   -0.553
27  -0.631   -0.635   -0.635
28      NA       NA       NA
29      NA       NA       NA
30      NA       NA       NA
31      NA       NA       NA
32      NA       NA       NA
33      NA       NA       NA
34  -0.013   -0.013   -0.013
35  -0.010   -0.010   -0.010
36   0.000    0.000    0.000
37  -0.033   -0.028   -0.028
38   0.064    0.059    0.059
39  -0.002   -0.001   -0.001
40   0.038    0.034    0.034
41  -0.086   -0.070   -0.070
42   0.067    0.061    0.061
43  -0.044   -0.041   -0.041
44   0.021    0.020    0.020
45   0.011    0.011    0.011
46   0.066    0.057    0.057
47   0.148    0.135    0.135
48  -0.169   -0.161   -0.161
49  -0.053   -0.048   -0.048
50   0.080    0.066    0.066
51  -0.042   -0.038   -0.038
52  -0.158   -0.148   -0.148
53   0.068    0.066    0.066
54   0.051    0.050    0.050
55   0.668    0.494    0.494
56  -0.973   -0.805   -0.805
57  -0.641   -0.578   -0.578
58  -0.359   -0.297   -0.297
59   0.363    0.245    0.245
60  -0.441   -0.366   -0.366
61   0.652    0.577    0.577
62  -0.436   -0.403   -0.403
63  -0.497   -0.478   -0.478
64   0.012    0.012    0.012
65  -0.001   -0.001   -0.001
66  -0.011   -0.011   -0.011
67   1.000    1.000    1.000
68   1.000    1.000    1.000
69  -1.000   -1.000   -1.000
70   0.004    0.004    0.004
71   0.001    0.001    0.001
72   0.000    0.000    0.000

16.10.6.6.4 Equivalence Test

The petersenlab package (Petersen, 2024b) contains the equiv_chi() function from Counsell et al. (2020) that performs an equivalence test: https://osf.io/cqu8v. The chi-square equivalence test is non-significant, suggesting that the model fit is not acceptable.

Code

equiv_chi(
  alpha = .05,
  chi = scalarInvarianceModel_chisquare,
  df = scalarInvarianceModel_df,
  m = 2,
  N_sample = scalarInvarianceModel_N,
  popRMSEA = .08)

Moreover, the equivalence test of the chi-square difference test is non-significant, suggesting that the degree of worsening of model fit is not acceptable. In other words, scalar invariance failed.

Code

scalarInvarianceModel_dfDiff <- 
  scalarInvarianceModel_df - metricInvarianceModel_df

equiv_chi(
  alpha = .05,
  chi = scalarInvarianceModel_chisquareDiff,
  df = scalarInvarianceModel_dfDiff,
  m = 2,
  N_sample = scalarInvarianceModel_N,
  popRMSEA = .08)

16.10.6.6.5 Permutation Test

Permutation procedures for testing measurement invariance are described in (Jorgensen et al., 2018). For reproducibility, I set the seed below. Using the same seed will yield the same answer every time. There is nothing special about this particular seed. You can specify the null model as the baseline model using: baseline.model = nullModelFit

Warning: this code takes a while to run based on 100 iterations. You can reduce the number of iterations to be faster.

Code

set.seed(52242)
scalarInvarianceTest <- permuteMeasEq(
  nPermute = numPermutations,
  modelType = "mgcfa",
  con = scalarInvarianceModel_fit,
  uncon = metricInvarianceModel_fit,
  AFIs = myAFIs,
  moreAFIs = moreAFIs,
  parallelType = "multicore", #only 'snow' works on Windows, but right now, it is throwing an error
  iseed = 52242)

Code

RNGkind("default", "default", "default")
set.seed(52242)

scalarInvarianceTest

Omnibus p value based on parametric chi-squared difference test:

Chisq diff    Df diff Pr(>Chisq) 
    41.928      6.000      0.000 


Omnibus p values based on nonparametric permutation method: 

             AFI.Difference p.value
chisq                40.641       0
chisq.scaled         41.486       0
rmsea                 0.016       0
cfi                  -0.040       0
tli                  -0.039       0
srmr                  0.011       0
rmsea.robust          0.015       0
cfi.robust           -0.038       0
tli.robust           -0.036       0

The p-values are significant, indicating that the model fit significantly worse than the metric invariance model. In other words, scalar invariance failed.

16.10.6.7 Internal Consistency Reliability

Internal consistency reliability of items composing the latent factors, as quantified by omega (\(\omega\)) and average variance extracted (AVE), was estimated using the semTools package (Jorgensen et al., 2021).

Code

compRelSEM(scalarInvarianceModel_fit)

Code

AVE(scalarInvarianceModel_fit)

16.10.6.8 Path Diagram

A path diagram of the model generated using the semPlot package (Epskamp, 2022) is below.

Code

semPaths(
  scalarInvarianceModel_fit,
  what = "est",
  layout = "tree2",
  ask = FALSE,
  edge.label.cex = 1.2)

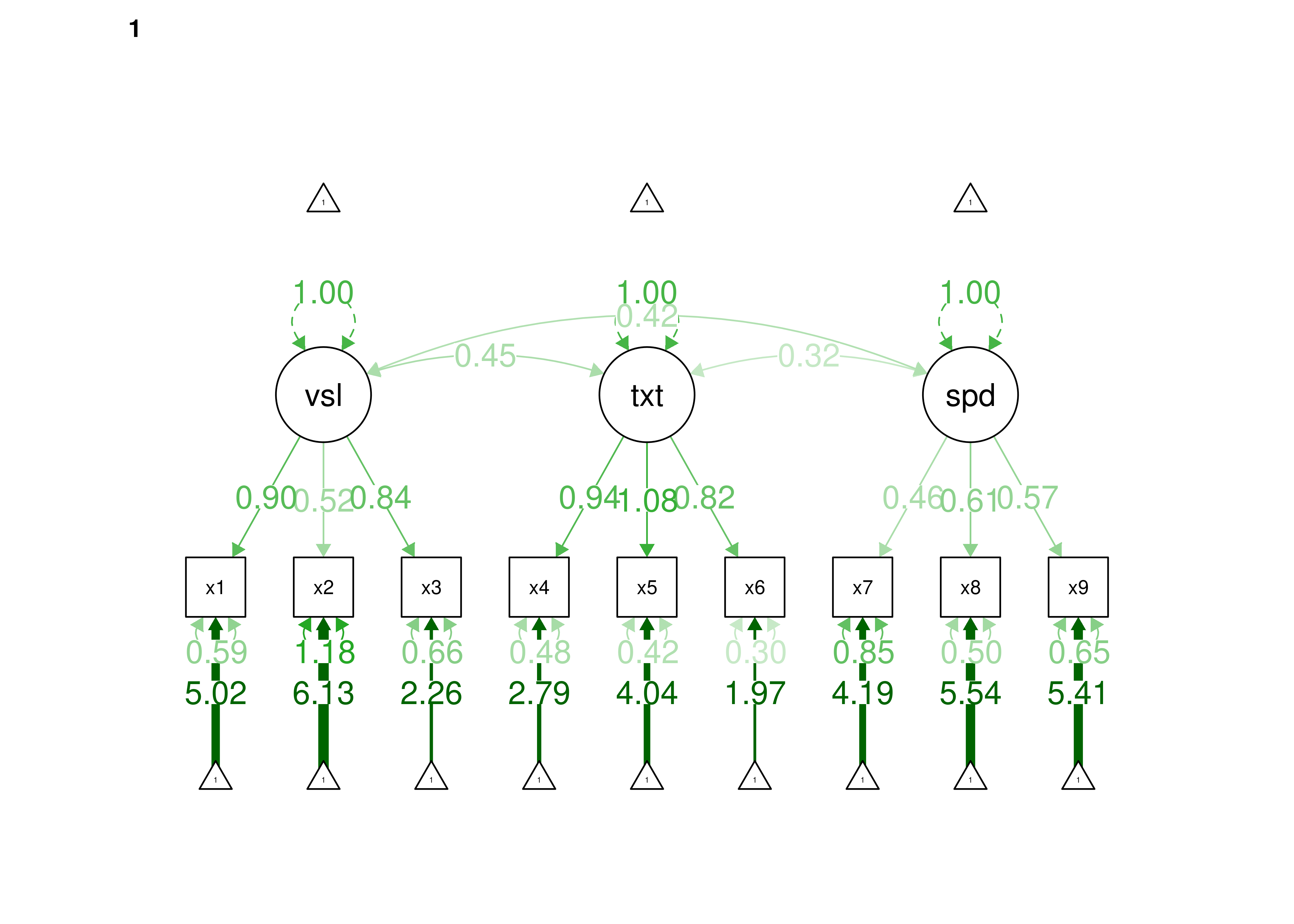
Figure 16.57: Scalar Invariance Model in Confirmatory Factor Analysis.

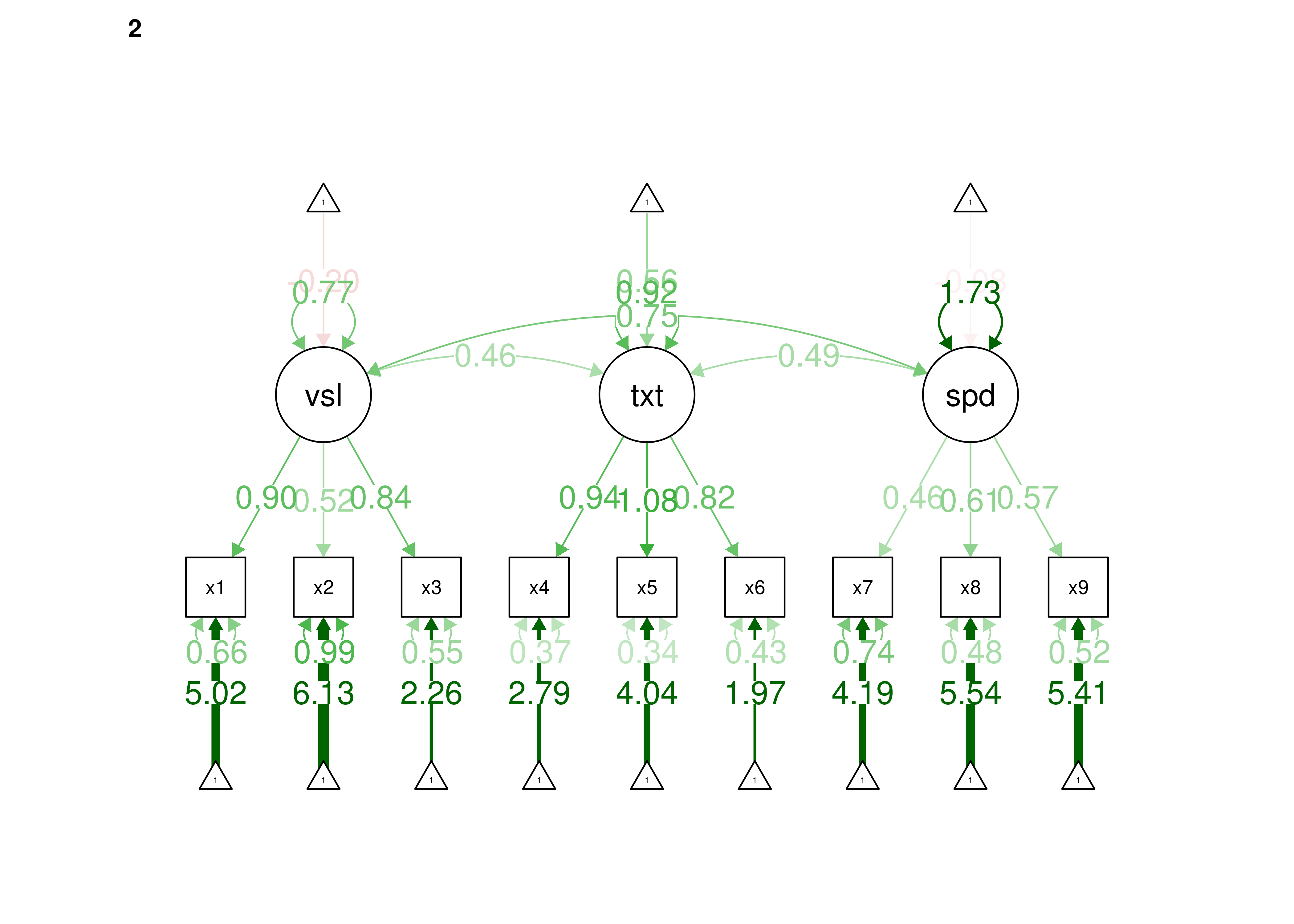
Figure 16.58: Scalar Invariance Model in Confirmatory Factor Analysis.

16.10.7 Residual (“Strict Factorial”) Invariance Model

Specify invariance of factor loadings, intercepts, and residuals across groups.

16.10.7.1 Model Syntax

Code

residualInvarianceModel <- measEq.syntax(
  configural.model = cfaModel,
  data = HolzingerSwineford1939,
  ID.fac = "std.lv",
  group = "school",
  group.equal = c("loadings","intercepts","residuals"))

Code

cat(as.character(residualInvarianceModel))

## LOADINGS:

visual =~ c(NA, NA)*x1 + c(lambda.1_1, lambda.1_1)*x1
visual =~ c(NA, NA)*x2 + c(lambda.2_1, lambda.2_1)*x2
visual =~ c(NA, NA)*x3 + c(lambda.3_1, lambda.3_1)*x3
textual =~ c(NA, NA)*x4 + c(lambda.4_2, lambda.4_2)*x4
textual =~ c(NA, NA)*x5 + c(lambda.5_2, lambda.5_2)*x5
textual =~ c(NA, NA)*x6 + c(lambda.6_2, lambda.6_2)*x6
speed =~ c(NA, NA)*x7 + c(lambda.7_3, lambda.7_3)*x7
speed =~ c(NA, NA)*x8 + c(lambda.8_3, lambda.8_3)*x8
speed =~ c(NA, NA)*x9 + c(lambda.9_3, lambda.9_3)*x9

## INTERCEPTS:

x1 ~ c(NA, NA)*1 + c(nu.1, nu.1)*1
x2 ~ c(NA, NA)*1 + c(nu.2, nu.2)*1
x3 ~ c(NA, NA)*1 + c(nu.3, nu.3)*1
x4 ~ c(NA, NA)*1 + c(nu.4, nu.4)*1
x5 ~ c(NA, NA)*1 + c(nu.5, nu.5)*1
x6 ~ c(NA, NA)*1 + c(nu.6, nu.6)*1
x7 ~ c(NA, NA)*1 + c(nu.7, nu.7)*1
x8 ~ c(NA, NA)*1 + c(nu.8, nu.8)*1
x9 ~ c(NA, NA)*1 + c(nu.9, nu.9)*1

## UNIQUE-FACTOR VARIANCES:

x1 ~~ c(NA, NA)*x1 + c(theta.1_1, theta.1_1)*x1
x2 ~~ c(NA, NA)*x2 + c(theta.2_2, theta.2_2)*x2
x3 ~~ c(NA, NA)*x3 + c(theta.3_3, theta.3_3)*x3
x4 ~~ c(NA, NA)*x4 + c(theta.4_4, theta.4_4)*x4
x5 ~~ c(NA, NA)*x5 + c(theta.5_5, theta.5_5)*x5
x6 ~~ c(NA, NA)*x6 + c(theta.6_6, theta.6_6)*x6
x7 ~~ c(NA, NA)*x7 + c(theta.7_7, theta.7_7)*x7
x8 ~~ c(NA, NA)*x8 + c(theta.8_8, theta.8_8)*x8
x9 ~~ c(NA, NA)*x9 + c(theta.9_9, theta.9_9)*x9

## LATENT MEANS/INTERCEPTS:

visual ~ c(0, NA)*1 + c(alpha.1.g1, alpha.1.g2)*1
textual ~ c(0, NA)*1 + c(alpha.2.g1, alpha.2.g2)*1
speed ~ c(0, NA)*1 + c(alpha.3.g1, alpha.3.g2)*1

## COMMON-FACTOR VARIANCES:

visual ~~ c(1, NA)*visual + c(psi.1_1.g1, psi.1_1.g2)*visual
textual ~~ c(1, NA)*textual + c(psi.2_2.g1, psi.2_2.g2)*textual
speed ~~ c(1, NA)*speed + c(psi.3_3.g1, psi.3_3.g2)*speed

## COMMON-FACTOR COVARIANCES:

visual ~~ c(NA, NA)*textual + c(psi.2_1.g1, psi.2_1.g2)*textual
visual ~~ c(NA, NA)*speed + c(psi.3_1.g1, psi.3_1.g2)*speed
textual ~~ c(NA, NA)*speed + c(psi.3_2.g1, psi.3_2.g2)*speed

Code

residualInvarianceSyntax <- as.character(residualInvarianceModel)

16.10.7.1.1 Summary of Model Features

Code

summary(residualInvarianceModel)

This lavaan model syntax specifies a CFA with 9 manifest indicators of 3 common factor(s).

To identify the location and scale of each common factor, the factor means and variances were fixed to 0 and 1, respectively, unless equality constraints on measurement parameters allow them to be freed.

Pattern matrix indicating num(eric), ord(ered), and lat(ent) indicators per factor:

   visual textual speed
x1 num                 
x2 num                 
x3 num                 
x4        num          
x5        num          
x6        num          
x7                num  
x8                num  
x9                num  

The following types of parameter were constrained to equality across groups:

    loadings
    intercepts
    residuals

16.10.7.2 Model Syntax in Table Form

Code

lavaanify(residualInvarianceModel, ngroups = 2)

Code

lavaanify(cfaModel_residualInvariance, ngroups = 2)

16.10.7.3 Fit the Model

Code

residualInvarianceModel_fit <- cfa(
  residualInvarianceSyntax,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

Code

residualInvarianceModelFullSyntax_fit <- lavaan(
  cfaModel_residualInvariance,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

16.10.7.4 Model Summary

Code

summary(
  residualInvarianceModel_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 62 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        66
  Number of equality constraints                    27

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               172.960     172.714
  Degrees of freedom                                69          69
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  1.001
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     87.707      87.707
    Grant-White                                 85.007      85.007

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.879       0.876
  Tucker-Lewis Index (TLI)                       0.874       0.871
                                                                  
  Robust Comparative Fit Index (CFI)                         0.883
  Robust Tucker-Lewis Index (TLI)                            0.878

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3680.600   -3680.600
  Scaling correction factor                                  0.645
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7439.201    7439.201
  Bayesian (BIC)                              7583.778    7583.778
  Sample-size adjusted Bayesian (SABIC)       7460.092    7460.092

Root Mean Square Error of Approximation:

  RMSEA                                          0.100       0.100
  90 Percent confidence interval - lower         0.082       0.081
  90 Percent confidence interval - upper         0.119       0.119
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    0.962       0.961
                                                                  
  Robust RMSEA                                               0.100
  90 Percent confidence interval - lower                     0.081
  90 Percent confidence interval - upper                     0.119
  P-value H_0: Robust RMSEA <= 0.050                         0.000
  P-value H_0: Robust RMSEA >= 0.080                         0.955

Standardized Root Mean Square Residual:

  SRMR                                           0.086       0.086

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.862    0.126    6.855    0.000    0.862    0.728
    x2      (l.2_)    0.516    0.091    5.678    0.000    0.516    0.436
    x3      (l.3_)    0.745    0.112    6.630    0.000    0.745    0.651
  textual =~                                                            
    x4      (l.4_)    0.928    0.071   13.094    0.000    0.928    0.828
    x5      (l.5_)    1.069    0.076   14.113    0.000    1.069    0.855
    x6      (l.6_)    0.882    0.062   14.125    0.000    0.882    0.830
  speed =~                                                              
    x7      (l.7_)    0.577    0.087    6.658    0.000    0.577    0.544
    x8      (l.8_)    0.669    0.083    8.109    0.000    0.669    0.688
    x9      (l.9_)    0.632    0.085    7.461    0.000    0.632    0.649

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.430    0.124    3.472    0.001    0.430    0.430
    speed  (p.3_1)    0.351    0.129    2.710    0.007    0.351    0.351
  textual ~~                                                            
    speed  (p.3_2)    0.302    0.093    3.250    0.001    0.302    0.302

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (nu.1)    5.025    0.095   52.938    0.000    5.025    4.243
   .x2      (nu.2)    6.138    0.086   71.711    0.000    6.138    5.188
   .x3      (nu.3)    2.332    0.099   23.546    0.000    2.332    2.039
   .x4      (nu.4)    2.784    0.086   32.453    0.000    2.784    2.483
   .x5      (nu.5)    4.030    0.102   39.369    0.000    4.030    3.224
   .x6      (nu.6)    1.928    0.075   25.828    0.000    1.928    1.815
   .x7      (nu.7)    4.270    0.076   55.911    0.000    4.270    4.027
   .x8      (nu.8)    5.619    0.075   74.597    0.000    5.619    5.775
   .x9      (nu.9)    5.470    0.073   74.756    0.000    5.470    5.616
    visual  (a.1.)    0.000                               0.000    0.000
    textual (a.2.)    0.000                               0.000    0.000
    speed   (a.3.)    0.000                               0.000    0.000

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.660    0.165    4.008    0.000    0.660    0.470
   .x2      (t.2_)    1.133    0.110   10.337    0.000    1.133    0.810
   .x3      (t.3_)    0.754    0.131    5.749    0.000    0.754    0.576
   .x4      (t.4_)    0.396    0.050    7.904    0.000    0.396    0.315
   .x5      (t.5_)    0.420    0.057    7.385    0.000    0.420    0.269
   .x6      (t.6_)    0.350    0.048    7.311    0.000    0.350    0.310
   .x7      (t.7_)    0.792    0.094    8.413    0.000    0.792    0.704
   .x8      (t.8_)    0.499    0.095    5.244    0.000    0.499    0.527
   .x9      (t.9_)    0.549    0.100    5.479    0.000    0.549    0.579
    visual  (p.1_)    1.000                               1.000    1.000
    textual (p.2_)    1.000                               1.000    1.000
    speed   (p.3_)    1.000                               1.000    1.000

R-Square:
                   Estimate
    x1                0.530
    x2                0.190
    x3                0.424
    x4                0.685
    x5                0.731
    x6                0.690
    x7                0.296
    x8                0.473
    x9                0.421


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (l.1_)    0.862    0.126    6.855    0.000    0.796    0.700
    x2      (l.2_)    0.516    0.091    5.678    0.000    0.476    0.408
    x3      (l.3_)    0.745    0.112    6.630    0.000    0.687    0.621
  textual =~                                                            
    x4      (l.4_)    0.928    0.071   13.094    0.000    0.926    0.827
    x5      (l.5_)    1.069    0.076   14.113    0.000    1.068    0.855
    x6      (l.6_)    0.882    0.062   14.125    0.000    0.881    0.830
  speed =~                                                              
    x7      (l.7_)    0.577    0.087    6.658    0.000    0.670    0.601
    x8      (l.8_)    0.669    0.083    8.109    0.000    0.777    0.740
    x9      (l.9_)    0.632    0.085    7.461    0.000    0.733    0.703

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textul  (p.2_)    0.519    0.135    3.852    0.000    0.563    0.563
    speed  (p.3_1)    0.643    0.202    3.183    0.001    0.600    0.600
  textual ~~                                                            
    speed  (p.3_2)    0.426    0.181    2.351    0.019    0.368    0.368

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (nu.1)    5.025    0.095   52.938    0.000    5.025    4.420
   .x2      (nu.2)    6.138    0.086   71.711    0.000    6.138    5.263
   .x3      (nu.3)    2.332    0.099   23.546    0.000    2.332    2.106
   .x4      (nu.4)    2.784    0.086   32.453    0.000    2.784    2.486
   .x5      (nu.5)    4.030    0.102   39.369    0.000    4.030    3.228
   .x6      (nu.6)    1.928    0.075   25.828    0.000    1.928    1.817
   .x7      (nu.7)    4.270    0.076   55.911    0.000    4.270    3.835
   .x8      (nu.8)    5.619    0.075   74.597    0.000    5.619    5.353
   .x9      (nu.9)    5.470    0.073   74.756    0.000    5.470    5.247
    visual  (a.1.)   -0.208    0.181   -1.149    0.251   -0.225   -0.225
    textual (a.2.)    0.611    0.132    4.646    0.000    0.612    0.612
    speed   (a.3.)   -0.283    0.155   -1.824    0.068   -0.244   -0.244

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .x1      (t.1_)    0.660    0.165    4.008    0.000    0.660    0.510
   .x2      (t.2_)    1.133    0.110   10.337    0.000    1.133    0.833
   .x3      (t.3_)    0.754    0.131    5.749    0.000    0.754    0.615
   .x4      (t.4_)    0.396    0.050    7.904    0.000    0.396    0.316
   .x5      (t.5_)    0.420    0.057    7.385    0.000    0.420    0.269
   .x6      (t.6_)    0.350    0.048    7.311    0.000    0.350    0.311
   .x7      (t.7_)    0.792    0.094    8.413    0.000    0.792    0.638
   .x8      (t.8_)    0.499    0.095    5.244    0.000    0.499    0.453
   .x9      (t.9_)    0.549    0.100    5.479    0.000    0.549    0.505
    visual  (p.1_)    0.852    0.217    3.932    0.000    1.000    1.000
    textual (p.2_)    0.997    0.193    5.160    0.000    1.000    1.000
    speed   (p.3_)    1.346    0.328    4.101    0.000    1.000    1.000

R-Square:
                   Estimate
    x1                0.490
    x2                0.167
    x3                0.385
    x4                0.684
    x5                0.731
    x6                0.689
    x7                0.362
    x8                0.547
    x9                0.495

Code

summary(
  residualInvarianceModelFullSyntax_fit,
  fit.measures = TRUE,
  standardized = TRUE,
  rsquare = TRUE)

lavaan 0.6-19 ended normally after 59 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        66
  Number of equality constraints                    27

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               172.960     172.714
  Degrees of freedom                                69          69
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  1.001
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     87.707      87.707
    Grant-White                                 85.007      85.007

Model Test Baseline Model:

  Test statistic                               932.665     909.019
  Degrees of freedom                                72          72
  P-value                                        0.000       0.000
  Scaling correction factor                                  1.026

User Model versus Baseline Model:

  Comparative Fit Index (CFI)                    0.879       0.876
  Tucker-Lewis Index (TLI)                       0.874       0.871
                                                                  
  Robust Comparative Fit Index (CFI)                         0.883
  Robust Tucker-Lewis Index (TLI)                            0.878

Loglikelihood and Information Criteria:

  Loglikelihood user model (H0)              -3680.600   -3680.600
  Scaling correction factor                                  0.645
      for the MLR correction                                      
  Loglikelihood unrestricted model (H1)      -3594.120   -3594.120
  Scaling correction factor                                  1.034
      for the MLR correction                                      
                                                                  
  Akaike (AIC)                                7439.201    7439.201
  Bayesian (BIC)                              7583.778    7583.778
  Sample-size adjusted Bayesian (SABIC)       7460.092    7460.092

Root Mean Square Error of Approximation:

  RMSEA                                          0.100       0.100
  90 Percent confidence interval - lower         0.082       0.081
  90 Percent confidence interval - upper         0.119       0.119
  P-value H_0: RMSEA <= 0.050                    0.000       0.000
  P-value H_0: RMSEA >= 0.080                    0.962       0.961
                                                                  
  Robust RMSEA                                               0.100
  90 Percent confidence interval - lower                     0.081
  90 Percent confidence interval - upper                     0.119
  P-value H_0: Robust RMSEA <= 0.050                         0.000
  P-value H_0: Robust RMSEA >= 0.080                         0.955

Standardized Root Mean Square Residual:

  SRMR                                           0.086       0.086

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.862    0.126    6.855    0.000    0.862    0.728
    x2      (lmb2)    0.516    0.091    5.678    0.000    0.516    0.436
    x3      (lmb3)    0.745    0.112    6.630    0.000    0.745    0.651
  textual =~                                                            
    x4      (lmb4)    0.928    0.071   13.094    0.000    0.928    0.828
    x5      (lmb5)    1.069    0.076   14.113    0.000    1.069    0.855
    x6      (lmb6)    0.882    0.062   14.125    0.000    0.882    0.830
  speed =~                                                              
    x7      (lmb7)    0.577    0.087    6.658    0.000    0.577    0.544
    x8      (lmb8)    0.669    0.083    8.110    0.000    0.669    0.688
    x9      (lmb9)    0.632    0.085    7.461    0.000    0.632    0.649

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.430    0.124    3.472    0.001    0.430    0.430
    speed             0.351    0.129    2.710    0.007    0.351    0.351
  textual ~~                                                            
    speed             0.302    0.093    3.250    0.001    0.302    0.302

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.000                               0.000    0.000
    textual           0.000                               0.000    0.000
    speed             0.000                               0.000    0.000
   .x1      (int1)    5.025    0.095   52.938    0.000    5.025    4.243
   .x2      (int2)    6.138    0.086   71.710    0.000    6.138    5.188
   .x3      (int3)    2.332    0.099   23.546    0.000    2.332    2.039
   .x4      (int4)    2.784    0.086   32.453    0.000    2.784    2.483
   .x5      (int5)    4.030    0.102   39.369    0.000    4.030    3.224
   .x6      (int6)    1.928    0.075   25.828    0.000    1.928    1.815
   .x7      (int7)    4.270    0.076   55.911    0.000    4.270    4.027
   .x8      (int8)    5.619    0.075   74.598    0.000    5.619    5.775
   .x9      (int9)    5.470    0.073   74.756    0.000    5.470    5.616

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            1.000                               1.000    1.000
    textual           1.000                               1.000    1.000
    speed             1.000                               1.000    1.000
   .x1      (rsd1)    0.660    0.165    4.008    0.000    0.660    0.470
   .x2      (rsd2)    1.133    0.110   10.337    0.000    1.133    0.810
   .x3      (rsd3)    0.754    0.131    5.749    0.000    0.754    0.576
   .x4      (rsd4)    0.396    0.050    7.904    0.000    0.396    0.315
   .x5      (rsd5)    0.420    0.057    7.385    0.000    0.420    0.269
   .x6      (rsd6)    0.350    0.048    7.311    0.000    0.350    0.310
   .x7      (rsd7)    0.792    0.094    8.414    0.000    0.792    0.704
   .x8      (rsd8)    0.499    0.095    5.244    0.000    0.499    0.527
   .x9      (rsd9)    0.549    0.100    5.479    0.000    0.549    0.579

R-Square:
                   Estimate
    x1                0.530
    x2                0.190
    x3                0.424
    x4                0.685
    x5                0.731
    x6                0.690
    x7                0.296
    x8                0.473
    x9                0.421


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual =~                                                             
    x1      (lmb1)    0.862    0.126    6.855    0.000    0.796    0.700
    x2      (lmb2)    0.516    0.091    5.678    0.000    0.476    0.408
    x3      (lmb3)    0.745    0.112    6.630    0.000    0.687    0.621
  textual =~                                                            
    x4      (lmb4)    0.928    0.071   13.094    0.000    0.926    0.827
    x5      (lmb5)    1.069    0.076   14.113    0.000    1.068    0.855
    x6      (lmb6)    0.882    0.062   14.125    0.000    0.881    0.830
  speed =~                                                              
    x7      (lmb7)    0.577    0.087    6.658    0.000    0.670    0.601
    x8      (lmb8)    0.669    0.083    8.110    0.000    0.777    0.740
    x9      (lmb9)    0.632    0.085    7.461    0.000    0.733    0.703

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  visual ~~                                                             
    textual           0.519    0.135    3.852    0.000    0.563    0.563
    speed             0.643    0.202    3.183    0.001    0.600    0.600
  textual ~~                                                            
    speed             0.426    0.181    2.351    0.019    0.368    0.368

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual           -0.208    0.181   -1.149    0.251   -0.225   -0.225
    textual           0.611    0.132    4.646    0.000    0.612    0.612
    speed            -0.283    0.155   -1.824    0.068   -0.244   -0.244
   .x1      (int1)    5.025    0.095   52.938    0.000    5.025    4.420
   .x2      (int2)    6.138    0.086   71.710    0.000    6.138    5.263
   .x3      (int3)    2.332    0.099   23.546    0.000    2.332    2.106
   .x4      (int4)    2.784    0.086   32.453    0.000    2.784    2.486
   .x5      (int5)    4.030    0.102   39.369    0.000    4.030    3.228
   .x6      (int6)    1.928    0.075   25.828    0.000    1.928    1.817
   .x7      (int7)    4.270    0.076   55.911    0.000    4.270    3.835
   .x8      (int8)    5.619    0.075   74.598    0.000    5.619    5.353
   .x9      (int9)    5.470    0.073   74.756    0.000    5.470    5.247

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
    visual            0.852    0.217    3.932    0.000    1.000    1.000
    textual           0.997    0.193    5.160    0.000    1.000    1.000
    speed             1.346    0.328    4.101    0.000    1.000    1.000
   .x1      (rsd1)    0.660    0.165    4.008    0.000    0.660    0.510
   .x2      (rsd2)    1.133    0.110   10.337    0.000    1.133    0.833
   .x3      (rsd3)    0.754    0.131    5.749    0.000    0.754    0.615
   .x4      (rsd4)    0.396    0.050    7.904    0.000    0.396    0.316
   .x5      (rsd5)    0.420    0.057    7.385    0.000    0.420    0.269
   .x6      (rsd6)    0.350    0.048    7.311    0.000    0.350    0.311
   .x7      (rsd7)    0.792    0.094    8.414    0.000    0.792    0.638
   .x8      (rsd8)    0.499    0.095    5.244    0.000    0.499    0.453
   .x9      (rsd9)    0.549    0.100    5.479    0.000    0.549    0.505

R-Square:
                   Estimate
    x1                0.490
    x2                0.167
    x3                0.385
    x4                0.684
    x5                0.731
    x6                0.689
    x7                0.362
    x8                0.547
    x9                0.495

16.10.7.5 Model Fit

You can specify the null model as the baseline model using: baseline.model = nullModelFit

Code

fitMeasures(residualInvarianceModel_fit)

                         npar                          fmin 
                       39.000                         0.287 
                        chisq                            df 
                      172.960                        69.000 
                       pvalue                  chisq.scaled 
                        0.000                       172.714 
                    df.scaled                 pvalue.scaled 
                       69.000                         0.000 
         chisq.scaling.factor                baseline.chisq 
                        1.001                       932.665 
                  baseline.df               baseline.pvalue 
                       72.000                         0.000 
        baseline.chisq.scaled            baseline.df.scaled 
                      909.019                        72.000 
       baseline.pvalue.scaled baseline.chisq.scaling.factor 
                        0.000                         1.026 
                          cfi                           tli 
                        0.879                         0.874 
                   cfi.scaled                    tli.scaled 
                        0.876                         0.871 
                   cfi.robust                    tli.robust 
                        0.883                         0.878 
                         nnfi                           rfi 
                        0.874                         0.806 
                          nfi                          pnfi 
                        0.815                         0.781 
                          ifi                           rni 
                        0.880                         0.879 
                  nnfi.scaled                    rfi.scaled 
                        0.871                         0.802 
                   nfi.scaled                   pnfi.scaled 
                        0.810                         0.776 
                   ifi.scaled                    rni.scaled 
                        0.877                         0.876 
                  nnfi.robust                    rni.robust 
                        0.878                         0.883 
                         logl             unrestricted.logl 
                    -3680.600                     -3594.120 
                          aic                           bic 
                     7439.201                      7583.778 
                       ntotal                          bic2 
                      301.000                      7460.092 
            scaling.factor.h1             scaling.factor.h0 
                        1.034                         0.645 
                        rmsea                rmsea.ci.lower 
                        0.100                         0.082 
               rmsea.ci.upper                rmsea.ci.level 
                        0.119                         0.900 
                 rmsea.pvalue                rmsea.close.h0 
                        0.000                         0.050 
        rmsea.notclose.pvalue             rmsea.notclose.h0 
                        0.962                         0.080 
                 rmsea.scaled         rmsea.ci.lower.scaled 
                        0.100                         0.081 
        rmsea.ci.upper.scaled           rmsea.pvalue.scaled 
                        0.119                         0.000 
 rmsea.notclose.pvalue.scaled                  rmsea.robust 
                        0.961                         0.100 
        rmsea.ci.lower.robust         rmsea.ci.upper.robust 
                        0.081                         0.119 
          rmsea.pvalue.robust  rmsea.notclose.pvalue.robust 
                        0.000                         0.955 
                          rmr                    rmr_nomean 
                        0.103                         0.102 
                         srmr                  srmr_bentler 
                        0.086                         0.086 
          srmr_bentler_nomean                          crmr 
                        0.083                         0.086 
                  crmr_nomean                    srmr_mplus 
                        0.083                         0.104 
            srmr_mplus_nomean                         cn_05 
                        0.084                       156.566 
                        cn_01                           gfi 
                      173.684                         0.992 
                         agfi                          pgfi 
                        0.988                         0.634 
                          mfi                          ecvi 
                        0.841                         0.834 

Code

residualInvarianceModelFitIndices <- fitMeasures(
  residualInvarianceModel_fit)[c(
    "cfi.robust", "rmsea.robust", "srmr")]

residualInvarianceModel_chisquare <- fitMeasures(
  residualInvarianceModel_fit)[c("chisq.scaled")]

residualInvarianceModel_chisquareScaling <- fitMeasures(
  residualInvarianceModel_fit)[c("chisq.scaling.factor")]

residualInvarianceModel_df <- fitMeasures(
  residualInvarianceModel_fit)[c("df.scaled")]

residualInvarianceModel_N <- lavInspect(
  residualInvarianceModel_fit,
  what = "ntotal")

16.10.7.6 Compare Model Fit

16.10.7.6.1 Nested Model (\(\chi^2\)) Difference Test

The scalar invariance model and the residual invariance model are considered “nested” models. The residual invariance model is nested within the scalar invariance model because the scalar invariance model includes all of the terms of the residual invariance model along with additional terms. Model fit of nested models can be compared with a chi-square difference test, also known as a likelihood ratio test or deviance test. A significant chi-square difference test would indicate that the simplified model with additional constraints (the residual invariance model) is significantly worse fitting than the more complex model that has fewer constraints (the scalar invariance model).

Code

anova(scalarInvarianceModel_fit, residualInvarianceModel_fit)

In this instance, you do not need to examine whether residual invariance held because the preceding level of measurement invariance (scalar invariance) did not hold.

The petersenlab package (Petersen, 2024b) contains the satorraBentlerScaledChiSquareDifferenceTestStatistic() function that performs a Satorra-Bentler scaled chi-square difference test:

Code

residualInvarianceModel_chisquareDiff <- 
  satorraBentlerScaledChiSquareDifferenceTestStatistic(
    T0 = residualInvarianceModel_chisquare,
    c0 = residualInvarianceModel_chisquareScaling,
    d0 = residualInvarianceModel_df,
    T1 = scalarInvarianceModel_chisquare,
    c1 = scalarInvarianceModel_chisquareScaling,
    d1 = scalarInvarianceModel_df)

residualInvarianceModel_chisquareDiff

chisq.scaled 
    14.35586 

16.10.7.6.2 Compare Other Fit Criteria

Code

round(residualInvarianceModelFitIndices - scalarInvarianceModelFitIndices,
      digits = 3)

  cfi.robust rmsea.robust         srmr 
      -0.007       -0.004        0.006 

16.10.7.6.3 Score-Based Test

Score-based tests of measurement invariance are implemented using the strucchange package and are described by T. Wang et al. (2014).

Code

coef(residualInvarianceModel_fit)

lambda.1_1 lambda.2_1 lambda.3_1 lambda.4_2 lambda.5_2 lambda.6_2 lambda.7_3 
     0.862      0.516      0.745      0.928      1.069      0.882      0.577 
lambda.8_3 lambda.9_3       nu.1       nu.2       nu.3       nu.4       nu.5 
     0.669      0.632      5.025      6.138      2.332      2.784      4.030 
      nu.6       nu.7       nu.8       nu.9  theta.1_1  theta.2_2  theta.3_3 
     1.928      4.270      5.619      5.470      0.660      1.133      0.754 
 theta.4_4  theta.5_5  theta.6_6  theta.7_7  theta.8_8  theta.9_9 psi.2_1.g1 
     0.396      0.420      0.350      0.792      0.499      0.549      0.430 
psi.3_1.g1 psi.3_2.g1 lambda.1_1 lambda.2_1 lambda.3_1 lambda.4_2 lambda.5_2 
     0.351      0.302      0.862      0.516      0.745      0.928      1.069 
lambda.6_2 lambda.7_3 lambda.8_3 lambda.9_3       nu.1       nu.2       nu.3 
     0.882      0.577      0.669      0.632      5.025      6.138      2.332 
      nu.4       nu.5       nu.6       nu.7       nu.8       nu.9  theta.1_1 
     2.784      4.030      1.928      4.270      5.619      5.470      0.660 
 theta.2_2  theta.3_3  theta.4_4  theta.5_5  theta.6_6  theta.7_7  theta.8_8 
     1.133      0.754      0.396      0.420      0.350      0.792      0.499 
 theta.9_9 alpha.1.g2 alpha.2.g2 alpha.3.g2 psi.1_1.g2 psi.2_2.g2 psi.3_3.g2 
     0.549     -0.208      0.611     -0.283      0.852      0.997      1.346 
psi.2_1.g2 psi.3_1.g2 psi.3_2.g2 
     0.519      0.643      0.426 

Code

coef(residualInvarianceModel_fit)[19:27]

theta.1_1 theta.2_2 theta.3_3 theta.4_4 theta.5_5 theta.6_6 theta.7_7 theta.8_8 
0.6598353 1.1333770 0.7536794 0.3957809 0.4196626 0.3504637 0.7916721 0.4987961 
theta.9_9 
0.5490913 

Code

strucchange::sctest(
  residualInvarianceModel_fit,
  order.by = HolzingerSwineford1939$school,
  parm = 19:27,
  functional = "LMuo")

    M-fluctuation test

data:  residualInvarianceModel_fit
f(efp) = 10.64, p-value = 0.3012

A score-based test and expected parameter change (EPC) estimates (Oberski, 2014; Oberski et al., 2015) are provided by the lavaan package (Rosseel et al., 2022).

Code

lavTestScore(
  residualInvarianceModel_fit,
  epc = TRUE
)

$test

total score test:

   test     X2 df p.value
1 score 60.136 27       0

$uni

univariate score tests:

     lhs op   rhs     X2 df p.value
1   .p1. == .p37.  0.011  1   0.915
2   .p2. == .p38.  0.043  1   0.836
3   .p3. == .p39.  0.062  1   0.803
4   .p4. == .p40.  0.089  1   0.766
5   .p5. == .p41.  4.083  1   0.043
6   .p6. == .p42.  5.815  1   0.016
7   .p7. == .p43.  0.026  1   0.872
8   .p8. == .p44.  0.003  1   0.954
9   .p9. == .p45.  0.006  1   0.939
10 .p10. == .p46.  6.331  1   0.012
11 .p11. == .p47.  7.812  1   0.005
12 .p12. == .p48. 20.213  1   0.000
13 .p13. == .p49.  1.231  1   0.267
14 .p14. == .p50.  1.155  1   0.283
15 .p15. == .p51.  0.001  1   0.982
16 .p16. == .p52. 14.986  1   0.000
17 .p17. == .p53.  3.574  1   0.059
18 .p18. == .p54.  1.735  1   0.188
19 .p19. == .p55.  0.055  1   0.815
20 .p20. == .p56.  2.026  1   0.155
21 .p21. == .p57.  1.867  1   0.172
22 .p22. == .p58.  0.754  1   0.385
23 .p23. == .p59.  0.619  1   0.432
24 .p24. == .p60.  3.852  1   0.050
25 .p25. == .p61.  2.273  1   0.132
26 .p26. == .p62.  0.674  1   0.412
27 .p27. == .p63.  1.954  1   0.162

$epc

expected parameter changes (epc) and expected parameter values (epv):

       lhs op     rhs block group free      label plabel    est    epc    epv
1   visual =~      x1     1     1    1 lambda.1_1   .p1.  0.862  0.083  0.945
2   visual =~      x2     1     1    2 lambda.2_1   .p2.  0.516 -0.017  0.499
3   visual =~      x3     1     1    3 lambda.3_1   .p3.  0.745 -0.095  0.650
4  textual =~      x4     1     1    4 lambda.4_2   .p4.  0.928 -0.006  0.922
5  textual =~      x5     1     1    5 lambda.5_2   .p5.  1.069  0.060  1.130
6  textual =~      x6     1     1    6 lambda.6_2   .p6.  0.882 -0.054  0.828
7    speed =~      x7     1     1    7 lambda.7_3   .p7.  0.577 -0.036  0.541
8    speed =~      x8     1     1    8 lambda.8_3   .p8.  0.669  0.006  0.676
9    speed =~      x9     1     1    9 lambda.9_3   .p9.  0.632 -0.028  0.604
10      x1 ~1             1     1   10       nu.1  .p10.  5.025 -0.076  4.949
11      x2 ~1             1     1   11       nu.2  .p11.  6.138 -0.154  5.984
12      x3 ~1             1     1   12       nu.3  .p12.  2.332  0.177  2.509
13      x4 ~1             1     1   13       nu.4  .p13.  2.784  0.030  2.814
14      x5 ~1             1     1   14       nu.5  .p14.  4.030 -0.029  4.002
15      x6 ~1             1     1   15       nu.6  .p15.  1.928  0.001  1.929
16      x7 ~1             1     1   16       nu.7  .p16.  4.270  0.168  4.439
17      x8 ~1             1     1   17       nu.8  .p17.  5.619 -0.055  5.564
18      x9 ~1             1     1   18       nu.9  .p18.  5.470 -0.043  5.427
19      x1 ~~      x1     1     1   19  theta.1_1  .p19.  0.660 -0.145  0.514
20      x2 ~~      x2     1     1   20  theta.2_2  .p20.  1.133  0.145  1.279
21      x3 ~~      x3     1     1   21  theta.3_3  .p21.  0.754  0.194  0.947
22      x4 ~~      x4     1     1   22  theta.4_4  .p22.  0.396  0.046  0.442
23      x5 ~~      x5     1     1   23  theta.5_5  .p23.  0.420  0.009  0.428
24      x6 ~~      x6     1     1   24  theta.6_6  .p24.  0.350 -0.059  0.291
25      x7 ~~      x7     1     1   25  theta.7_7  .p25.  0.792  0.115  0.906
26      x8 ~~      x8     1     1   26  theta.8_8  .p26.  0.499  0.016  0.515
27      x9 ~~      x9     1     1   27  theta.9_9  .p27.  0.549  0.084  0.633
28  visual ~1             1     1    0 alpha.1.g1  .p28.  0.000     NA     NA
29 textual ~1             1     1    0 alpha.2.g1  .p29.  0.000     NA     NA
30   speed ~1             1     1    0 alpha.3.g1  .p30.  0.000     NA     NA
31  visual ~~  visual     1     1    0 psi.1_1.g1  .p31.  1.000     NA     NA
32 textual ~~ textual     1     1    0 psi.2_2.g1  .p32.  1.000     NA     NA
33   speed ~~   speed     1     1    0 psi.3_3.g1  .p33.  1.000     NA     NA
34  visual ~~ textual     1     1   28 psi.2_1.g1  .p34.  0.430 -0.002  0.428
35  visual ~~   speed     1     1   29 psi.3_1.g1  .p35.  0.351  0.007  0.358
36 textual ~~   speed     1     1   30 psi.3_2.g1  .p36.  0.302  0.007  0.309
37  visual =~      x1     2     2   31 lambda.1_1  .p37.  0.862  0.000  0.862
38  visual =~      x2     2     2   32 lambda.2_1  .p38.  0.516  0.063  0.579
39  visual =~      x3     2     2   33 lambda.3_1  .p39.  0.745 -0.024  0.721
40 textual =~      x4     2     2   34 lambda.4_2  .p40.  0.928  0.036  0.963
41 textual =~      x5     2     2   35 lambda.5_2  .p41.  1.069 -0.091  0.978
42 textual =~      x6     2     2   36 lambda.6_2  .p42.  0.882  0.061  0.944
43   speed =~      x7     2     2   37 lambda.7_3  .p43.  0.577 -0.035  0.542
44   speed =~      x8     2     2   38 lambda.8_3  .p44.  0.669  0.020  0.689
45   speed =~      x9     2     2   39 lambda.9_3  .p45.  0.632  0.033  0.665
46      x1 ~1             2     2   40       nu.1  .p46.  5.025  0.075  5.100
47      x2 ~1             2     2   41       nu.2  .p47.  6.138  0.176  6.314
48      x3 ~1             2     2   42       nu.3  .p48.  2.332 -0.197  2.135
49      x4 ~1             2     2   43       nu.4  .p49.  2.784 -0.057  2.726
50      x5 ~1             2     2   44       nu.5  .p50.  4.030  0.085  4.115
51      x6 ~1             2     2   45       nu.6  .p51.  1.928 -0.040  1.888
52      x7 ~1             2     2   46       nu.7  .p52.  4.270 -0.185  4.086
53      x8 ~1             2     2   47       nu.8  .p53.  5.619  0.074  5.694
54      x9 ~1             2     2   48       nu.9  .p54.  5.470  0.065  5.535
55      x1 ~~      x1     2     2   49  theta.1_1  .p55.  0.660  0.021  0.681
56      x2 ~~      x2     2     2   50  theta.2_2  .p56.  1.133 -0.162  0.971
57      x3 ~~      x3     2     2   51  theta.3_3  .p57.  0.754 -0.091  0.663
58      x4 ~~      x4     2     2   52  theta.4_4  .p58.  0.396 -0.064  0.332
59      x5 ~~      x5     2     2   53  theta.5_5  .p59.  0.420  0.009  0.428
60      x6 ~~      x6     2     2   54  theta.6_6  .p60.  0.350  0.062  0.412
61      x7 ~~      x7     2     2   55  theta.7_7  .p61.  0.792 -0.088  0.704
62      x8 ~~      x8     2     2   56  theta.8_8  .p62.  0.499 -0.044  0.455
63      x9 ~~      x9     2     2   57  theta.9_9  .p63.  0.549 -0.095  0.454
64  visual ~1             2     2   58 alpha.1.g2  .p64. -0.208  0.009 -0.200
65 textual ~1             2     2   59 alpha.2.g2  .p65.  0.611  0.002  0.614
66   speed ~1             2     2   60 alpha.3.g2  .p66. -0.283 -0.016 -0.298
67  visual ~~  visual     2     2   61 psi.1_1.g2  .p67.  0.852  0.016  0.868
68 textual ~~ textual     2     2   62 psi.2_2.g2  .p68.  0.997 -0.004  0.993
69   speed ~~   speed     2     2   63 psi.3_3.g2  .p69.  1.346  0.008  1.354
70  visual ~~ textual     2     2   64 psi.2_1.g2  .p70.  0.519 -0.002  0.517
71  visual ~~   speed     2     2   65 psi.3_1.g2  .p71.  0.643 -0.014  0.629
72 textual ~~   speed     2     2   66 psi.3_2.g2  .p72.  0.426 -0.009  0.417
   sepc.lv sepc.all sepc.nox
1    0.083    0.070    0.070
2   -0.017   -0.014   -0.014
3   -0.095   -0.083   -0.083
4   -0.006   -0.005   -0.005
5    0.060    0.048    0.048
6   -0.054   -0.051   -0.051
7   -0.036   -0.034   -0.034
8    0.006    0.006    0.006
9   -0.028   -0.029   -0.029
10  -0.076   -0.065   -0.065
11  -0.154   -0.130   -0.130
12   0.177    0.155    0.155
13   0.030    0.027    0.027
14  -0.029   -0.023   -0.023
15   0.001    0.001    0.001
16   0.168    0.159    0.159
17  -0.055   -0.057   -0.057
18  -0.043   -0.044   -0.044
19  -0.660   -0.470   -0.470
20   1.133    0.810    0.810
21   0.754    0.576    0.576
22   0.396    0.315    0.315
23   0.420    0.269    0.269
24  -0.350   -0.310   -0.310
25   0.792    0.704    0.704
26   0.499    0.527    0.527
27   0.549    0.579    0.579
28      NA       NA       NA
29      NA       NA       NA
30      NA       NA       NA
31      NA       NA       NA
32      NA       NA       NA
33      NA       NA       NA
34  -0.002   -0.002   -0.002
35   0.007    0.007    0.007
36   0.007    0.007    0.007
37   0.000    0.000    0.000
38   0.058    0.050    0.050
39  -0.022   -0.020   -0.020
40   0.036    0.032    0.032
41  -0.091   -0.073   -0.073
42   0.061    0.058    0.058
43  -0.041   -0.037   -0.037
44   0.023    0.022    0.022
45   0.038    0.037    0.037
46   0.075    0.066    0.066
47   0.176    0.151    0.151
48  -0.197   -0.178   -0.178
49  -0.057   -0.051   -0.051
50   0.085    0.068    0.068
51  -0.040   -0.038   -0.038
52  -0.185   -0.166   -0.166
53   0.074    0.071    0.071
54   0.065    0.063    0.063
55   0.660    0.510    0.510
56  -1.133   -0.833   -0.833
57  -0.754   -0.615   -0.615
58  -0.396   -0.316   -0.316
59   0.420    0.269    0.269
60   0.350    0.311    0.311
61  -0.792   -0.638   -0.638
62  -0.499   -0.453   -0.453
63  -0.549   -0.505   -0.505
64   0.009    0.009    0.009
65   0.002    0.002    0.002
66  -0.013   -0.013   -0.013
67   1.000    1.000    1.000
68  -1.000   -1.000   -1.000
69   1.000    1.000    1.000
70  -0.002   -0.002   -0.002
71  -0.013   -0.013   -0.013
72  -0.007   -0.007   -0.007

16.10.7.6.4 Equivalence Test

The petersenlab package (Petersen, 2024b) contains the equiv_chi() function from Counsell et al. (2020) that performs an equivalence test: https://osf.io/cqu8v. The chi-square equivalence test is non-significant, suggesting that the model fit is not acceptable. The equivalence test of the chi-square difference test is non-significant, suggesting that the degree of worsening of model fit is not acceptable.

Code

equiv_chi(
  alpha = .05,
  chi = residualInvarianceModel_chisquare,
  df = residualInvarianceModel_df,
  m = 2,
  N_sample = residualInvarianceModel_N,
  popRMSEA = .08)

Moreover, the equivalence test of the chi-square difference test is non-significant, suggesting that the degree of worsening of model fit is not acceptable. In other words, residual invariance failed.

Code

residualInvarianceModel_dfDiff <- 
  residualInvarianceModel_df - scalarInvarianceModel_df

equiv_chi(
  alpha = .05,
  chi = residualInvarianceModel_chisquareDiff,
  df = residualInvarianceModel_dfDiff,
  m = 2,
  N_sample = residualInvarianceModel_N,
  popRMSEA = .08)

16.10.7.6.5 Permutation Test

Permutation procedures for testing measurement invariance are described in (Jorgensen et al., 2018). For reproducibility, I set the seed below. Using the same seed will yield the same answer every time. There is nothing special about this particular seed. You can specify the null model as the baseline model using: baseline.model = nullModelFit.

Warning: this code takes a while to run based on \(100\) iterations. You can reduce the number of iterations to be faster.

Code

set.seed(52242)
residualInvarianceTest <- permuteMeasEq(
  nPermute = numPermutations,
  modelType = "mgcfa",
  con = residualInvarianceModel_fit,
  uncon = scalarInvarianceModel_fit,
  AFIs = myAFIs,
  moreAFIs = moreAFIs,
  parallelType = "multicore", #only 'snow' works on Windows, but right now, it is throwing an error
  iseed = 52242)

Code

RNGkind("default", "default", "default")
set.seed(52242)

residualInvarianceTest

Omnibus p value based on parametric chi-squared difference test:

Chisq diff    Df diff Pr(>Chisq) 
    14.356      9.000      0.110 


Omnibus p values based on nonparametric permutation method: 

             AFI.Difference p.value
chisq                16.006    0.15
chisq.scaled         13.272    0.24
rmsea                -0.004    0.38
cfi                  -0.008    0.15
tli                   0.009    0.52
srmr                  0.006    0.20
rmsea.robust         -0.004    0.38
cfi.robust           -0.007    0.15
tli.robust            0.010    0.50

The p-values are non-significant, indicating that the model did not fit significantly worse than the scalar invariance model.

16.10.7.7 Internal Consistency Reliability

Internal consistency reliability of items composing the latent factors, as quantified by omega (\(\omega\)) and average variance extracted (AVE), was estimated using the semTools package (Jorgensen et al., 2021).

Code

compRelSEM(residualInvarianceModel_fit)

Code

AVE(residualInvarianceModel_fit)

16.10.7.8 Path Diagram

A path diagram of the model generated using the semPlot package (Epskamp, 2022) is below.

Code

semPaths(
  residualInvarianceModel_fit,
  what = "est",
  layout = "tree2",
  ask = FALSE,
  edge.label.cex = 1.2)

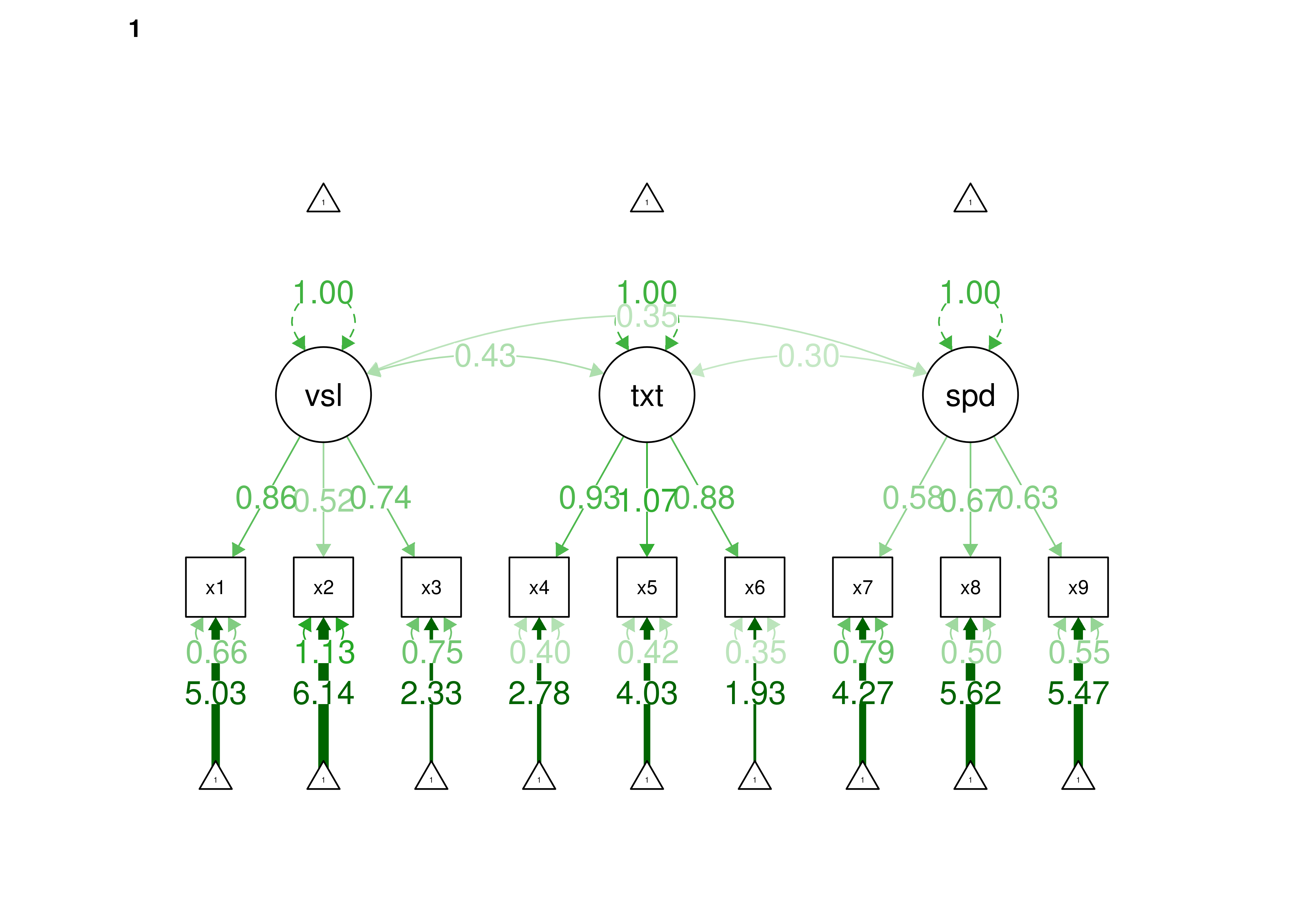
Figure 16.59: Residual Invariance Model in Confirmatory Factor Analysis.

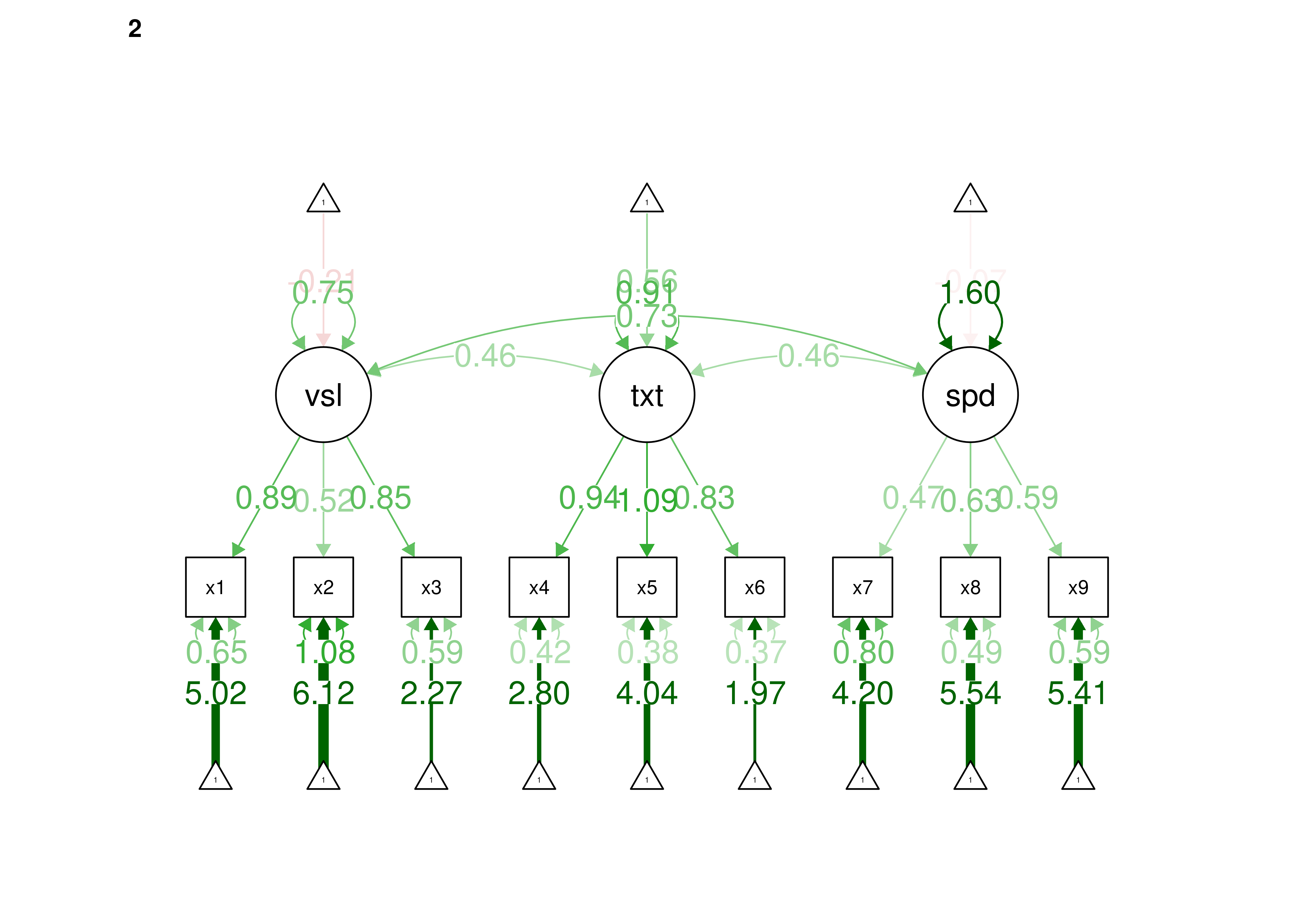
Figure 16.60: Residual Invariance Model in Confirmatory Factor Analysis.

16.10.8 Addressing Measurement Non-Invariance

In the example above, we detected measurement non-invariance of intercepts, but not factor loadings. Thus, we would want to identify which item(s) show non-invariant intercepts across groups. When detecting measurement non-invariance in a given parameter (e.g., factor loadings, intercepts, or residuals), one can identify the specific items that show measurement non-invariance in one of two primary ways: (1) starting with a model that allows the given parameter to differ across groups, a researcher can iteratively add constraints to identify the item(s) for which measurement invariance fails, or (2) starting with a model that constrains the given parameter to be the same across groups, a researcher can iteratively remove constraints to identify the item(s) for which measurement invariance becomes established (and by process of elimination, the items for which measurement invariance does not become established).

16.10.8.1 Iteratively add constraints to identify measurement non-invariance

In the example above, we detected measurement non-invariance of intercepts. One approach to identify measurement non-invariance is to iteratively add constraints to a model that allows the given parameter (intercepts) to differ across groups. So, we will use the metric invariance model as the baseline model (in which item intercepts are allowed to differ across groups), and iteratively add constraints to identify which item(s) show non-invariant intercepts across groups.

16.10.8.1.1 Variable 1

Variable 1 does not have non-invariant intercepts.

Code

cfaModel_metricInvarianceV1 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV1_fit <- lavaan(
  cfaModel_metricInvarianceV1,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV1_fit)

16.10.8.1.2 Variable 2

Variable 2 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV2 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ c(intx1, intx1)*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV2_fit <- lavaan(
  cfaModel_metricInvarianceV2,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV2_fit)

Variable 2 appears to have larger intercepts in group 2 than in group 1:

Code

summary(metricInvarianceModel_fit)

lavaan 0.6-19 ended normally after 73 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                        63
  Number of equality constraints                     9

  Number of observations per group:                   
    Pasteur                                        156
    Grant-White                                    145
  Number of missing patterns per group:               
    Pasteur                                          9
    Grant-White                                      9

Model Test User Model:
                                              Standard      Scaled
  Test Statistic                               116.313     117.955
  Degrees of freedom                                54          54
  P-value (Chi-square)                           0.000       0.000
  Scaling correction factor                                  0.986
    Yuan-Bentler correction (Mplus variant)                       
  Test statistic for each group:
    Pasteur                                     64.366      64.366
    Grant-White                                 53.590      53.590

Parameter Estimates:

  Standard errors                             Sandwich
  Information bread                           Observed
  Observed information based on                Hessian


Group 1 [Pasteur]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  visual =~                                           
    x1      (l.1_)    0.885    0.122    7.258    0.000
    x2      (l.2_)    0.536    0.088    6.106    0.000
    x3      (l.3_)    0.707    0.087    8.148    0.000
  textual =~                                          
    x4      (l.4_)    0.935    0.072   12.929    0.000
    x5      (l.5_)    1.045    0.076   13.740    0.000
    x6      (l.6_)    0.874    0.070   12.496    0.000
  speed =~                                            
    x7      (l.7_)    0.550    0.075    7.346    0.000
    x8      (l.8_)    0.675    0.087    7.784    0.000
    x9      (l.9_)    0.602    0.088    6.867    0.000

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)
  visual ~~                                           
    textul  (p.2_)    0.473    0.105    4.484    0.000
    speed  (p.3_1)    0.347    0.125    2.778    0.005
  textual ~~                                          
    speed  (p.3_2)    0.320    0.096    3.342    0.001

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .x1      (n.1.)    4.948    0.095   52.314    0.000
   .x2      (n.2.)    5.984    0.098   60.949    0.000
   .x3      (n.3.)    2.510    0.093   26.891    0.000
   .x4      (n.4.)    2.814    0.091   30.886    0.000
   .x5      (n.5.)    4.002    0.105   38.265    0.000
   .x6      (n.6.)    1.929    0.079   24.377    0.000
   .x7      (n.7.)    4.439    0.087   51.128    0.000
   .x8      (n.8.)    5.564    0.079   70.170    0.000
   .x9      (n.9.)    5.426    0.080   67.539    0.000
    visual  (a.1.)    0.000                           
    textual (a.2.)    0.000                           
    speed   (a.3.)    0.000                           

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
   .x1      (t.1_)    0.577    0.166    3.482    0.000
   .x2      (t.2_)    1.252    0.162    7.718    0.000
   .x3      (t.3_)    0.853    0.127    6.737    0.000
   .x4      (t.4_)    0.447    0.072    6.189    0.000
   .x5      (t.5_)    0.486    0.075    6.445    0.000
   .x6      (t.6_)    0.258    0.057    4.499    0.000
   .x7      (t.7_)    0.860    0.114    7.549    0.000
   .x8      (t.8_)    0.512    0.097    5.296    0.000
   .x9      (t.9_)    0.635    0.118    5.376    0.000
    visual  (p.1_)    1.000                           
    textual (p.2_)    1.000                           
    speed   (p.3_)    1.000                           


Group 2 [Grant-White]:

Latent Variables:
                   Estimate  Std.Err  z-value  P(>|z|)
  visual =~                                           
    x1      (l.1_)    0.885    0.122    7.258    0.000
    x2      (l.2_)    0.536    0.088    6.106    0.000
    x3      (l.3_)    0.707    0.087    8.148    0.000
  textual =~                                          
    x4      (l.4_)    0.935    0.072   12.929    0.000
    x5      (l.5_)    1.045    0.076   13.740    0.000
    x6      (l.6_)    0.874    0.070   12.496    0.000
  speed =~                                            
    x7      (l.7_)    0.550    0.075    7.346    0.000
    x8      (l.8_)    0.675    0.087    7.784    0.000
    x9      (l.9_)    0.602    0.088    6.867    0.000

Covariances:
                   Estimate  Std.Err  z-value  P(>|z|)
  visual ~~                                           
    textul  (p.2_)    0.520    0.134    3.867    0.000
    speed  (p.3_1)    0.638    0.211    3.023    0.002
  textual ~~                                          
    speed  (p.3_2)    0.429    0.193    2.219    0.026

Intercepts:
                   Estimate  Std.Err  z-value  P(>|z|)
   .x1      (n.1.)    4.930    0.096   51.453    0.000
   .x2      (n.2.)    6.198    0.092   67.063    0.000
   .x3      (n.3.)    1.992    0.086   23.042    0.000
   .x4      (n.4.)    3.318    0.093   35.501    0.000
   .x5      (n.5.)    4.714    0.097   48.693    0.000
   .x6      (n.6.)    2.467    0.094   26.165    0.000
   .x7      (n.7.)    3.923    0.087   45.299    0.000
   .x8      (n.8.)    5.488    0.087   63.174    0.000
   .x9      (n.9.)    5.338    0.085   62.628    0.000
    visual  (a.1.)    0.000                           
    textual (a.2.)    0.000                           
    speed   (a.3.)    0.000                           

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)
   .x1      (t.1_)    0.652    0.168    3.877    0.000
   .x2      (t.2_)    0.940    0.145    6.473    0.000
   .x3      (t.3_)    0.606    0.113    5.376    0.000
   .x4      (t.4_)    0.348    0.066    5.257    0.000
   .x5      (t.5_)    0.371    0.074    5.021    0.000
   .x6      (t.6_)    0.439    0.076    5.738    0.000
   .x7      (t.7_)    0.622    0.098    6.338    0.000
   .x8      (t.8_)    0.410    0.148    2.765    0.006
   .x9      (t.9_)    0.505    0.128    3.957    0.000
    visual  (p.1_)    0.910    0.234    3.895    0.000
    textual (p.2_)    1.004    0.191    5.257    0.000
    speed   (p.3_)    1.498    0.357    4.201    0.000

Thus, in subsequent models, we would allow variable 2 to have different intercepts across groups.

16.10.8.1.3 Variable 3

Variable 3 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV3 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ c(intx1, intx1)*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV3_fit <- lavaan(
  cfaModel_metricInvarianceV3,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV3_fit)

16.10.8.1.4 Variable 4

Variable 4 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV4 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ c(intx1, intx1)*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV4_fit <- lavaan(
  cfaModel_metricInvarianceV4,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV4_fit)

16.10.8.1.5 Variable 5

Variable 5 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV5 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ c(intx1, intx1)*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV5_fit <- lavaan(
  cfaModel_metricInvarianceV5,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV5_fit)

16.10.8.1.6 Variable 6

Variable 6 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV6 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ c(intx1, intx1)*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV6_fit <- lavaan(
  cfaModel_metricInvarianceV6,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV6_fit)

16.10.8.1.7 Variable 7

Variable 7 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV7 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ c(intx1, intx1)*1
 x8 ~ NA*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV7_fit <- lavaan(
  cfaModel_metricInvarianceV7,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV7_fit)

16.10.8.1.8 Variable 8

Variable 8 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV8 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ c(intx1, intx1)*1
 x9 ~ NA*1
'

cfaModel_metricInvarianceV8_fit <- lavaan(
  cfaModel_metricInvarianceV8,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV8_fit)

16.10.8.1.9 Variable 9

Variable 9 has non-invariant intercepts.

Code

cfaModel_metricInvarianceV9 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively fix intercepts of manifest variables across groups
 x1 ~ c(intx1, intx1)*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ c(intx1, intx1)*1
'

cfaModel_metricInvarianceV9_fit <- lavaan(
  cfaModel_metricInvarianceV9,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_metricInvarianceV9_fit)

16.10.8.1.10 Summary

When iteratively adding constraints, item 1 showed measurement invariance of intercepts, but all other items showed measurement non-invariance of intercepts. This could be due to the selection of starting with item 1 as the first constraint. We could try applying constraints in a different order to see the extent to which the order influences which items are identified as showing measurement non-invariance.

16.10.8.2 Iteratively drop constraints to identify measurement non-invariance

Another approach to identify measurement non-invariance is to iteratively drop constraints to a model that constrains the given parameter (intercepts) to be the same across groups. So, we will use the scalar invariance model as the baseline model (in which item intercepts are constrained to be the same across groups), and we will iteratively drop constraints to identify the items for which measurement invariance becomes established (relative to the metric invariance model which allows item intercepts to differ across groups), and therefore, identifies which item(s) show non-invariant intercepts across groups.

16.10.8.2.1 Variable 1

Measurement invariance does not yet become established when freeing intercepts of variable 1 across groups. This suggests that, whether or not variable 1 shows non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV1 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ c(intx2, intx2)*1
 x3 ~ c(intx3, intx3)*1
 x4 ~ c(intx4, intx4)*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV1_fit <- lavaan(
  cfaModel_scalarInvarianceV1,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV1_fit)

16.10.8.2.2 Variable 2

Measurement invariance does not yet become established when freeing intercepts of variable 2 across groups. This suggests that, whether or not variables 1 and 2 show non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV2 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ c(intx3, intx3)*1
 x4 ~ c(intx4, intx4)*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV2_fit <- lavaan(
  cfaModel_scalarInvarianceV2,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV2_fit)

16.10.8.2.3 Variable 3

Measurement invariance does not yet become established when freeing intercepts of variable 3 across groups. This suggests that, whether or not variables 1, 2, and 3 show non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV3 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ c(intx4, intx4)*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV3_fit <- lavaan(
  cfaModel_scalarInvarianceV3,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV3_fit)

16.10.8.2.4 Variable 4

Measurement invariance does not yet become established when freeing intercepts of variable 4 across groups. This suggests that, whether or not variables 1, 2, 3, and 4 show non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV4 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ c(intx5, intx5)*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV4_fit <- lavaan(
  cfaModel_scalarInvarianceV4,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV4_fit)

16.10.8.2.5 Variable 5

Measurement invariance does not yet become established when freeing intercepts of variable 5 across groups. This suggests that, whether or not variables 1, 2, 3, 4, and 5 show non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV5 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ c(intx6, intx6)*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV5_fit <- lavaan(
  cfaModel_scalarInvarianceV5,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV5_fit)

16.10.8.2.6 Variable 6

Measurement invariance does not yet become established when freeing intercepts of variable 6 across groups. This suggests that, whether or not variables 1, 2, 3, 4, 5, and 6 show non-invariant intercepts, there are other items that show non-invariant intercepts.

Code

cfaModel_scalarInvarianceV6 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ c(intx7, intx7)*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV6_fit <- lavaan(
  cfaModel_scalarInvarianceV6,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV6_fit)

16.10.8.2.7 Variable 7

Measurement invariance becomes established when freeing intercepts of variable 7 across groups. This suggests that item 7 shows non-invariant intercepts across groups, and that measurement invariance holds when constraining items 8 and 9 to be invariant across groups. There may also be other items, especially among the preceding items (variables 1–6), that show non-invariant intercepts across groups.

Code

cfaModel_scalarInvarianceV7 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV7_fit <- lavaan(
  cfaModel_scalarInvarianceV7,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV7_fit)

16.10.8.2.8 Variable 8

Measurement invariance continues to hold when freeing intercepts of variable 8 across groups. This suggests that variable 8 does not show non-invariant intercepts across groups, at least when the other intercepts have been freed.

Code

cfaModel_scalarInvarianceV8 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ NA*1
 x9 ~ c(intx9, intx9)*1
'

cfaModel_scalarInvarianceV8_fit <- lavaan(
  cfaModel_scalarInvarianceV8,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV8_fit)

16.10.8.2.9 Variable 9

Measurement invariance continues to hold when freeing intercepts of variable 9 across groups (even after constraining intercepts of variable 8 across groups). This suggests that variable 9 does not show non-invariant intercepts across groups, at least when the other intercepts have been freed.

Code

cfaModel_scalarInvarianceV9 <- '
 #Fix factor loadings to be the same across groups
 visual  =~ c(lambdax1,lambdax1)*x1 + c(lambdax2,lambdax2)*x2 + c(lambdax3,lambdax3)*x3
 textual =~ c(lambdax4,lambdax4)*x4 + c(lambdax5,lambdax5)*x5 + c(lambdax6,lambdax6)*x6
 speed   =~ c(lambdax7,lambdax7)*x7 + c(lambdax8,lambdax8)*x8 + c(lambdax9,lambdax9)*x9
 
 #Fix latent means to zero
 visual ~ 0
 textual ~ 0
 speed ~ 0
 
 #Fix latent variances to one in group 1; free latent variances in group 2
 visual ~~ c(1, NA)*visual
 textual ~~ c(1, NA)*textual
 speed ~~ c(1, NA)*speed
 
 #Estimate covariances among latent variables
 visual ~~ textual
 visual ~~ speed
 textual ~~ speed
 
 #Estimate residual variances of manifest variables
 x1 ~~ x1
 x2 ~~ x2
 x3 ~~ x3
 x4 ~~ x4
 x5 ~~ x5
 x6 ~~ x6
 x7 ~~ x7
 x8 ~~ x8
 x9 ~~ x9
 
 #Iteratively free intercepts across groups
 x1 ~ NA*1
 x2 ~ NA*1
 x3 ~ NA*1
 x4 ~ NA*1
 x5 ~ NA*1
 x6 ~ NA*1
 x7 ~ NA*1
 x8 ~ c(intx8, intx8)*1
 x9 ~ NA*1
'

cfaModel_scalarInvarianceV9_fit <- lavaan(
  cfaModel_scalarInvarianceV9,
  data = HolzingerSwineford1939,
  group = "school",
  missing = "ML",
  estimator = "MLR")

anova(metricInvarianceModel_fit, cfaModel_scalarInvarianceV9_fit)

16.10.8.2.10 Summary

When iteratively dropping constraints, measurement invariance became established when freeing the intercepts for items 1–7 across groups. This suggests that items 7, 8, and 9 show measurement invariance of intercepts across groups. This could be due to the selection of starting with item 1 as the first constraint to be freed. We could try freeing constraints in a different order to see the extent to which the order influences which items are identified as showing measurement non-invariance.

16.10.8.3 Next Steps

After identifying which item(s) show measurement non-invariance, we would evaluate the measurement non-invariance according to theory and effect sizes. We might start with the item with the largest measurement non-invariance. If we deem the measurement non-invariance for this item is non-negligible, we have three primary options: (1) drop the item for both groups, (2) drop the item for one group but keep it for the other group, or (3) freely estimate parameters for the item across groups. We would do this iteratively for the remaining items, by magnitude, that show non-negligible measurement non-invariance. Thus, our model might show partial scalar invariance—some items might have intercepts that are constrained to be the same across groups, whereas other items might have intercepts that are allowed to differ across groups. Then, we would test subsequent measurement invariance models (e.g., residual invariance) while keeping the partially freed constaints from the partial scalar invariance model. Once we establish the best fitting model that makes as many constraints that are theoretically and empirically justified for the purposes of the study, we would use that model in subsequent tests. As a reminder, full or partial metric invariance is helpful for comparing associations across groups, whereas full or partial scalar invariance is helpful for comparing mean levels across groups.

16.11 Conclusion

Bias is a systematic error. Test bias refers to a systematic error (in measurement, prediction, etc.) as a function of group membership. The two broad categories of test bias include predictive bias and test structure bias. Predictive bias refers to differences between groups in the relation between the test and criterion—i.e., different intercepts and/or slopes of the regression line between the test and the criterion. Test structure bias refers to differences in the internal test characteristics across groups, and can be evaluated with approaches such as measurement invariance and differential item function. When detecting test bias, it is important to address it, and there are a number of ways of correcting for bias, including score adjustment and other approaches that do not involve score adjustment. However, even if a test does not show bias, it does not mean that the test is fair. Fairness is not a scientific question but rather a moral, societal, and ethical question; there are many different ways of operationalizing fairness. Fairness is a complex question, so do the best you can and try to minimize any negative impact of the assessment procedures.

16.12 Suggested Readings

Putnick & Bornstein (2016); N. S. Cole (1981); Fernández & Abe (2018); Reynolds & Suzuki (2012); Sackett & Wilk (1994); Jonson & Geisinger (2022)

16.13 Exercises

16.13.1 Questions

Note: Several of the following questions use data from the Children of the National Longitudinal Survey of Youth Survey (CNLSY). The CNLSY is a publicly available longitudinal data set provided by the Bureau of Labor Statistics (https://www.bls.gov/nls/nlsy79-children.htm#topical-guide; archived at https://perma.cc/EH38-HDRN). The CNLSY data file for these exercises is located on the book’s page of the Open Science Framework (https://osf.io/3pwza). Children’s behavior problems were rated in 1988 (time 1: T1) and then again in 1990 (time 2: T2) on the Behavior Problems Index (BPI). Below are the items corresponding to the Antisocial subscale of the BPI:

1. cheats or tells lies
2. bullies or is cruel/mean to others
3. does not seem to feel sorry after misbehaving
4. breaks things deliberately
5. is disobedient at school
6. has trouble getting along with teachers
7. has sudden changes in mood or feeling

1. 1. Determine whether there is predictive bias, as a function of sex, in predicting antisocial behavior at T2 using antisocial behavior at T2. Describe any predictive bias observed.
   2. How could you address this predictive bias?
2. Assume that children are selected to receive preventative services if their score on the Antisocial scale at T1 is > 6. Assume that children at T2 have an antisocial disorder if their score at T2 is > 6. Does the Antisocial scale show fairness in terms of equal outcomes between boys and girls?
3. A lawyer argues in court that a test that is used to select students for college admissions should be able to be used because it has been demonstrated to show no evidence of bias against particular groups. However, you know that just because a measure may be unbiased does not mean that using the measure’s scores for that purpose is fair. How could such a measure be unbiased yet unfair?
4. Fit a multi-group item response theory model to the Antisocial subscale at time 2, with the participant’s sex as a grouping factor.
   1. Does a model with item parameters constrained across sexes fit significantly worse than a model with item parameters that are allowed to vary across sexes?
   2. Starting with an unconstrained model that allows item parameters to vary across sexes, sequentially add constraints to item parameters across groups. Which items differed in discrimination across groups? Which items differed in severity across groups? Describe any differences.
   3. How could any differential item functioning be addressed?
5. Examine the longitudinal measurement invariance of the Antisocial scale across T1 and T2. Use full information maximum likelihood (FIML) to account for missing data. Use robust standard errors to account for non-normally distributed data. Which type(s) of longitudinal measurement invariance failed? Which items and parameters appeared to differ across ages?

16.13.2 Answers

1. 1. There is predictive bias in terms of different slopes across sexes. The slope is steeper for boys than girls, indicating that the measure is not as predictively accurate for girls as it is for boys.
   2. You could address this predictive bias by using a different predictive measure for girls than boys, changing the criterion, or by using within-group norming.
2. No, the Antisocial scale does not show equal outcomes in terms of selection rate. The selection ratio is much lower in girls \((0.10)\) compared to boys \((0.05)\).
3. The measure could be unbiased if it shows the same intercepts and slopes across groups in predicting college performance. However, a measure can still be unfair even it is unbiased. If there are different types of errors in different groups, the measure may not be fair. For instance, if there are more false negative errors in Black applicants compared to White applicants and more false positive errors in White applicants than Black applicants, the measure would be unfair against Black applicants. Even if the percent accuracy of prediction is the same for Black and White applicants, the errors have different implications for each group—White applicants who would have failed in college are more likely to be accepted whereas strong Black applicants who would have succeeded are less likely to be accepted. To address the unfairness of the test, it will be important to use one of the various operationalizations of fairness: equal outcomes, equal opportunity, or equal odds.
4. 1. The model with item parameters constrained across sexes fit significantly worse than a model with item parameters that were allowed to vary across sexes, \(\chi^2[-19] = -119.12, p < .001\). This suggests that the item parameters show differential item functioning across boys and girls.
   2. No items showed significant differences in discrimination across sexes, suggesting that items did not differ in their relation to the latent factor across boys and girls. Items 1, 2, 3, 4, 5, and 6 differed in severity across sexes. Items showed greater severity for girls than boys. It took a higher level of antisocial behavior for a girl to be endorsed as engaging in one of the following behaviors: cheats or tells lies, bullies or is cruel/mean to others, does not seem to feel sorry after misbehaving, breaks things deliberately, is disobedient at school, and has trouble getting along with teachers.
   3. The differences in item severity across boys and girls could be addressed by resolving DIF. That is, the items that show severity DIF (items 1–6) would be allowed to differ in their severity parameter across boys and girls, but these items would be constrained to have the same discrimination across groups; non-DIF items would have severity and discrimination parameters constrained to be the same across groups.
5. The configural invariance model fit well according to RMSEA \((0.09)\) and SRMR \((0.06)\), but fit less well according to CFI \((0.77)\). The metric invariance model did not fit significantly worse than the configural invariance model \((\Delta\chi^2[6] = 8.77, p = 0.187)\). However, the scalar invariance model fit significantly worse than the metric invariance model \((\Delta\chi^2[6] = 21.28, p = 0.002)\), and the residual invariance model fit significantly worse than the scalar invariance model \((\Delta\chi^2[7] = 42.80, p < .001)\). Therefore, scalar and residual invariance failed. The following items showed larger intercepts at T1 compared to T2: items 1, 2, 3, 4, 5, and 7. Only item 6 showed larger intercepts at T2 than T1. The following items showed a larger residual at T1 compared to T2: items 2–7. Only item 1 showed a larger residual at T2 compared to T1.

References

Aguinis, H., Culpepper, S. A., & Pierce, C. A. (2010). Revival of test bias research in preemployment testing. Journal of Applied Psychology, 95(4), 648–680. https://doi.org/10.1037/a0018714

American Educational Research Association, American Psychological Association, & National Council on Measurement in Education. (2014). Standards for educational and psychological testing. American Educational Research Association.

Barrash, J., Stillman, A., Anderson, S. W., Uc, E. Y., Dawson, J. D., & Rizzo, M. (2010). Prediction of driving ability with neuropsychological tests: Demographic adjustments diminish accuracy. Journal of the International Neuropsychological Society, 16(4), 679–686. https://doi.org/10.1017/S1355617710000470

Bauer, D. J., Belzak, W. C. M., & Cole, V. T. (2020). Simplifying the assessment of measurement invariance over multiple background variables: Using regularized moderated nonlinear factor analysis to detect differential item functioning. Structural Equation Modeling: A Multidisciplinary Journal, 27(1), 43–55. https://doi.org/10.1080/10705511.2019.1642754

Belzak, W. C. M., & Bauer, D. J. (2020). Improving the assessment of measurement invariance: Using regularization to select anchor items and identify differential item functioning. Psychological Methods, 25(6), 673–690. https://doi.org/10.1037/met0000253

Brown, R. T., Reynolds, C. R., & Whitaker, J. S. (1999). Bias in mental testing since bias in mental testing. School Psychology Quarterly, 14(3), 208–238. https://doi.org/10.1037/h0089007

Burlew, A. K., Peteet, B. J., McCuistian, C., & Miller-Roenigk, B. D. (2019). Best practices for researching diverse groups. American Journal of Orthopsychiatry, 89(3), 354–368. https://doi.org/10.1037/ort0000350

Camilli, G. (2013). Ongoing issues in test fairness. Educational Research and Evaluation, 19(2–3), 104–120. https://doi.org/10.1080/13803611.2013.767602

Chalmers, P. (2020). mirt: Multidimensional item response theory. https://CRAN.R-project.org/package=mirt

Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal, 14(3), 464–504. https://doi.org/10.1080/10705510701301834

Cheng, Y., Shao, C., & Lathrop, Q. N. (2016). The mediated MIMIC model for understanding the underlying mechanism of DIF. Educational and Psychological Measurement, 76(1), 43–63. https://doi.org/10.1177/0013164415576187

Cheung, G. W., & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural Equation Modeling: A Multidisciplinary Journal, 9(2), 233–255. https://doi.org/10.1207/s15328007sem0902_5

Clark, M. J., & Grandy, J. (1984). Sex differences in the academic performance of Scholastic Aptitude Test takers: College board report no. 84-8. College Board Publications.

Cole, N. S. (1981). Bias in testing. American Psychologist, 36(10), 1067–1077. https://doi.org/10.1037/0003-066X.36.10.1067

Cole, V., Gottfredson, N., & Giordano, M. (2018). aMNLFA: Automated fitting of moderated nonlinear factor analysis through the Mplus program. https://CRAN.R-project.org/package=aMNLFA

Committee on the General Aptitude Test Battery, Commission on Behavioral and Social Sciences and Education, & National Research Council. (1989). Fairness in employment testing: Validity generalization, minority issues, and the general aptitude test battery. National Academies Press.

Counsell, A., Cribbie, R. A., & Flora, D. B. (2020). Evaluating equivalence testing methods for measurement invariance. Multivariate Behavioral Research, 55(2), 312–328. https://doi.org/10.1080/00273171.2019.1633617

Curran, P. J., Howard, A. L., Bainter, S. A., Lane, S. T., & McGinley, J. S. (2014). The separation of between-person and within-person components of individual change over time: A latent curve model with structured residuals. Journal of Consulting and Clinical Psychology, 82, 8–94. https://doi.org/10.1037/a0035297

Dorans, N. J. (2017). Contributions to the quantitative assessment of item, test, and score fairness. In R. E. Bennett & M. von Davier (Eds.), Advancing human assessment (pp. 201–230). Springer, Cham.

Dueber, D. (2019). dmacs: Measurement nonequivalence effect size calculator. https://github.com/ddueber/dmacs

Epskamp, S. (2022). semPlot: Path diagrams and visual analysis of various SEM packages’ output. https://github.com/SachaEpskamp/semPlot

Fernández, A. L., & Abe, J. (2018). Bias in cross-cultural neuropsychological testing: Problems and possible solutions. Culture and Brain, 6(1), 1–35. https://doi.org/10.1007/s40167-017-0050-2

Fletcher, R. R., Nakeshimana, A., & Olubeko, O. (2021). Addressing fairness, bias, and appropriate use of artificial intelligence and machine learning in global health. Frontiers in Artificial Intelligence, 3(116). https://doi.org/10.3389/frai.2020.561802

Gipps, C., & Stobart, G. (2009). Fairness in assessment. In C. Wyatt-Smith & J. J. Cumming (Eds.), Educational assessment in the 21st century: Connecting theory and practice (pp. 105–118). Springer Netherlands. https://doi.org/10.1007/978-1-4020-9964-9_6

Gonzalez, O., & Pelham, W. E. (2021). When does differential item functioning matter for screening? A method for empirical evaluation. Assessment, 28(2), 446–456. https://doi.org/10.1177/1073191120913618

Gottfredson, L. S. (1994). The science and politics of race-norming. American Psychologist, 49(11), 955–963. https://doi.org/10.1037/0003-066X.49.11.955

Gottfredson, N. C., Cole, V. T., Giordano, M. L., Bauer, D. J., Hussong, A. M., & Ennett, S. T. (2019). Simplifying the implementation of modern scale scoring methods with an automated R package: Automated moderated nonlinear factor analysis (aMNLFA). Addictive Behaviors, 94, 65–73. https://doi.org/10.1016/j.addbeh.2018.10.031

Gunn, H. J., Grimm, K. J., & Edwards, M. C. (2020). Evaluation of six effect size measures of measurement non-invariance for continuous outcomes. Structural Equation Modeling: A Multidisciplinary Journal, 27(4), 503–514. https://doi.org/10.1080/10705511.2019.1689507

Hagquist, C. (2019). Explaining differential item functioning focusing on the crucial role of external information – an example from the measurement of adolescent mental health. BMC Medical Research Methodology, 19(1), 185. https://doi.org/10.1186/s12874-019-0828-3

Hagquist, C., & Andrich, D. (2017). Recent advances in analysis of differential item functioning in health research using the Rasch model. Health and Quality of Life Outcomes, 15(1), 181. https://doi.org/10.1186/s12955-017-0755-0

Hall, G. C. N., Bansal, A., & Lopez, I. R. (1999). Ethnicity and psychopathology: A meta-analytic review of 31 years of comparative MMPI/MMPI-2 research. Psychological Assessment, 11(2), 186–197. https://doi.org/10.1037/1040-3590.11.2.186

Han, K., Colarelli, S. M., & Weed, N. C. (2019). Methodological and statistical advances in the consideration of cultural diversity in assessment: A critical review of group classification and measurement invariance testing. Psychological Assessment, 31(12), 1481–1496. https://doi.org/10.1037/pas0000731

Helms, J. E. (2006). Fairness is not validity or cultural bias in racial-group assessment: A quantitative perspective. American Psychologist, 61(8), 845–859. https://doi.org/10.1037/0003-066X.61.8.845

Jensen, A. R. (1980). Précis of bias in mental testing. Behavioral and Brain Sciences, 3(3), 325–333. https://doi.org/10.1017/S0140525X00005161

Jonson, J. L., & Geisinger, K. F. (2022). Fairness in educational and psychological testing: Examining theoretical, research, practice, and policy implications of the 2014 standards. American Educational Research Association,.

Jorgensen, T. D., Kite, B. A., Chen, P.-Y., & Short, S. D. (2018). Permutation randomization methods for testing measurement equivalence and detecting differential item functioning in multiple-group confirmatory factor analysis. Psychological Methods, 23(4), 708–728. https://doi.org/10.1037/met0000152

Jorgensen, T. D., Pornprasertmanit, S., Schoemann, A. M., & Rosseel, Y. (2021). semTools: Useful tools for structural equation modeling. https://github.com/simsem/semTools/wiki

Kuncel, N. R., & Hezlett, S. A. (2010). Fact and fiction in cognitive ability testing for admissions and hiring decisions. Current Directions in Psychological Science, 19(6), 339–345. https://doi.org/10.1177/0963721410389459

Lai, M. H. C. (2021). Adjusting for measurement noninvariance with alignment in growth modeling. Multivariate Behavioral Research, 1–18. https://doi.org/10.1080/00273171.2021.1941730

Lee, K., Bull, R., & Ho, R. M. H. (2013). Developmental changes in executive functioning. Child Development, 84(6), 1933–1953. https://doi.org/10.1111/cdev.12096

Little, T. D. (2013). Longitudinal structural equation modeling. The Guilford Press.

Little, T. D., Preacher, K. J., Selig, J. P., & Card, N. A. (2007). New developments in latent variable panel analyses of longitudinal data. International Journal of Behavioral Development, 31(4), 357–365. https://doi.org/10.1177/0165025407077757

Little, T. D., Slegers, D. W., & Card, N. A. (2006). A non-arbitrary method of identifying and scaling latent variables in SEM and MACS models. Structural Equation Modeling, 13(1), 59–72. https://doi.org/10.1207/s15328007sem1301_3

Liu, Y., Millsap, R. E., West, S. G., Tein, J.-Y., Tanaka, R., & Grimm, K. J. (2017). Testing measurement invariance in longitudinal data with ordered-categorical measures. Psychological Methods, 22(3), 486–506. https://doi.org/10.1037/met0000075

Manly, J. J. (2005). Advantages and disadvantages of separate norms for African Americans. The Clinical Neuropsychologist, 19(2), 270–275. https://doi.org/10.1080/13854040590945346

Manly, J. J., & Echemendia, R. J. (2007). Race-specific norms: Using the model of hypertension to understand issues of race, culture, and education in neuropsychology. Archives of Clinical Neuropsychology, 22(3), 319–325. https://doi.org/10.1016/j.acn.2007.01.006

McClelland, D. C. (1973). Testing for competence rather than for “intelligence.” American Psychologist, 28, 1–14. https://doi.org/10.1037/h0034092

Meade, A. W. (2010). A taxonomy of effect size measures for the differential functioning of items and scales. Journal of Applied Psychology, 95(4), 728–743. https://doi.org/10.1037/a0018966

Melikyan, Z. A., Agranovich, A. V., & Puente, A. E. (2019). Fairness in psychological testing. In G. Goldstein, D. N. Allen, & J. DeLuca (Eds.), Handbook of psychological assessment (fourth edition) (pp. 551–572). Academic Press. https://doi.org/10.1016/B978-0-12-802203-0.00018-3

Millsap, R. E. (2011). Statistical approaches to measurement invariance. Taylor & Francis.

Muthén, L. K., & Muthén, B. O. (2019). Mplus version 8.4. Muthén & Muthén.

Nye, C. D., Bradburn, J., Olenick, J., Bialko, C., & Drasgow, F. (2019). How big are my effects? Examining the magnitude of effect sizes in studies of measurement equivalence. Organizational Research Methods, 22(3), 678–709. https://doi.org/10.1177/1094428118761122

Oberski, D. L. (2014). Evaluating sensitivity of parameters of interest to measurement invariance in latent variable models. Political Analysis, 22(1), 45–60. https://doi.org/10.1093/pan/mpt014

Oberski, D. L., Vermunt, J. K., & Moors, G. B. D. (2015). Evaluating measurement invariance in categorical data latent variable models with the EPC-interest. Political Analysis, 23(4), 550–563. https://doi.org/10.1093/pan/mpv020

Paulus, J. K., & Kent, D. M. (2020). Predictably unequal: Understanding and addressing concerns that algorithmic clinical prediction may increase health disparities. Npj Digital Medicine, 3(1), 99. https://doi.org/10.1038/s41746-020-0304-9

Petersen, I. T. (2024b). petersenlab: A collection of R functions by the Petersen Lab. https://doi.org/10.32614/CRAN.package.petersenlab

Petersen, I. T., Choe, D. E., & LeBeau, B. (2020). Studying a moving target in development: The challenge and opportunity of heterotypic continuity. Developmental Review, 58, 100935. https://doi.org/10.1016/j.dr.2020.100935

Putnick, D. L., & Bornstein, M. H. (2016). Measurement invariance conventions and reporting: The state of the art and future directions for psychological research. Developmental Review, 41, 71–90. https://doi.org/10.1016/j.dr.2016.06.004

Raykov, T., Marcoulides, G. A., Harrison, M., & Zhang, M. (2020). On the dependability of a popular procedure for studying measurement invariance: A cause for concern? Structural Equation Modeling: A Multidisciplinary Journal, 27(4), 649–656. https://doi.org/10.1080/10705511.2019.1610409

Reynolds, C. R., Altmann, R. A., & Allen, D. N. (2021). The problem of bias in psychological assessment. In C. R. Reynolds, R. A. Altmann, & D. N. Allen (Eds.), Mastering modern psychological testing: Theory and methods (pp. 573–613). Springer International Publishing. https://doi.org/10.1007/978-3-030-59455-8_15

Reynolds, C. R., & Suzuki, L. A. (2012). Bias in psychological assessment: An empirical review and recommendations. In I. B. Weiner, J. R. Graham, & J. A. Naglieri (Eds.), Handbook of psychology, Vol. 10: Assessment psychology, Part 1: Assessment issues (2nd ed., pp. 82–113).

Robitzsch, A. (2019). mnlfa: Moderated nonlinear factor analysis. https://CRAN.R-project.org/package=mnlfa

Rosseel, Y., Jorgensen, T. D., & Rockwood, N. (2022). lavaan: Latent variable analysis. https://lavaan.ugent.be

Sackett, P. R., Borneman, M. J., & Connelly, B. S. (2008). High stakes testing in higher education and employment: Appraising the evidence for validity and fairness. American Psychologist, 63, 215–227. https://doi.org/10.1037/0003-066X.63.4.215

Sackett, P. R., Schmitt, N., Ellingson, J. E., & Kabin, M. B. (2001). High-stakes testing in employment, credentialing, and higher education. American Psychologist, 56, 301–318. https://doi.org/10.1037/0003-066X.56.4.302

Sackett, P. R., & Wilk, S. L. (1994). Within-group norming and other forms of score adjustment in preemployment testing. American Psychologist, 49(11), 929–954. https://doi.org/10.1037/0003-066X.49.11.929

Schmidt, F. L., & Hunter, J. E. (1981). Employment testing: Old theories and new research findings. American Psychologist, 36(10), 1128–1137. https://doi.org/10.1037/0003-066X.36.10.1128

Silverberg, N. D., & Millis, S. R. (2009). Impairment versus deficiency in neuropsychological assessment: Implications for ecological validity. Journal of the International Neuropsychological Society, 15(1), 94–102. https://doi.org/10.1017/S1355617708090139

Thorndike, R. L. (1971). Concepts of culture-fairness. Journal of Educational Measurement, 8(2), 63–70. https://doi.org/10.1111/j.1745-3984.1971.tb00907.x

Van De Schoot, R., Kluytmans, A., Tummers, L., Lugtig, P., Hox, J., & Muthen, B. (2013). Facing off with scylla and charybdis: A comparison of scalar, partial, and the novel possibility of approximate measurement invariance. Frontiers in Psychology, 4(770). https://doi.org/10.3389/fpsyg.2013.00770

Van De Schoot, R., Schmidt, P., De Beuckelaer, A., Lek, K., & Zondervan-Zwijnenburg, M. (2015). Editorial: Measurement invariance. Frontiers in Psychology, 6(1064). https://doi.org/10.3389/fpsyg.2015.01064

Wang, T., Merkle, E. C., & Zeileis, A. (2014). Score-based tests of measurement invariance: Use in practice. Frontiers in Psychology, 5. https://doi.org/10.3389/fpsyg.2014.00438

Wang, W.-C., Shih, C.-L., & Yang, C.-C. (2009). The MIMIC method with scale purification for detecting differential item functioning. Educational and Psychological Measurement, 69(5), 713–731. https://doi.org/10.1177/0013164409332228

Youngstrom, E. A., & Van Meter, A. (2016). Empirically supported assessment of children and adolescents. Clinical Psychology: Science and Practice, 23(4), 327–347. https://doi.org/10.1111/cpsp.12172

Zieky, M. J. (2006). Fairness review in assessment. In S. M. Downing & T. M. Haladyna (Eds.), Handbook of test development (pp. 359–376). Routledge. https://doi.org/10.4324/9780203874776.ch16

Zieky, M. J. (2013). Fairness review in assessment. In K. F. Geisinger, B. A. Bracken, J. F. Carlson, J.-I. C. Hansen, N. R. Kuncel, S. P. Reise, & M. C. Rodriguez (Eds.), APA handbook of testing and assessment in psychology, Vol. 1: Test theory and testing and assessment in industrial and organizational psychology (pp. 293–302). American Psychological Association. https://doi.org/10.1037/14047-017

Feedback

Please consider providing feedback about this textbook, so that I can make it as helpful as possible. You can provide feedback at the following link: https://forms.gle/95iW4p47cuaphTek6