I need your help!

I want your feedback to make the book better for you and other readers. If you find typos, errors, or places where the text may be improved, please let me know. The best ways to provide feedback are by GitHub or hypothes.is annotations.

You can leave a comment at the bottom of the page/chapter, or open an issue or submit a pull request on GitHub: https://github.com/isaactpetersen/Fantasy-Football-Analytics-Textbook

Hypothesis Alternatively, you can leave an annotation using hypothes.is. To add an annotation, select some text and then click the symbol on the pop-up menu. To see the annotations of others, click the symbol in the upper right-hand corner of the page.

25  Time Series Analysis

This chapter provides an overview of time series analysis.

25.1 Getting Started

25.1.1 Load Packages

Code
library("petersenlab")
library("xts")
library("zoo")
library("forecast")
library("brms")
library("rstan")
library("plotly")
library("tidyverse")

25.1.2 Load Data

Code
load(file = "./data/player_stats_weekly.RData")
load(file = "./data/player_stats_seasonal.RData")

We created the player_stats_weekly.RData and player_stats_seasonal.RData objects in Section 4.4.3. The following code loads the Bayesian model object that was fit in Section 12.4.5.

Code
load(url("https://osf.io/download/q6rjf/")) # Bayesian model object

25.2 Overview of Time Series Analysis

Time series analysis is useful when trying to generate forecasts from longitudinal data. That is, time series analysis seeks to evaluate change over time to predict future values.

There many different types of time series analyses. For simplicity, in this chapter, we use autoregressive integrated moving average (ARIMA) and exponential smoothing models to demonstrate one approach to time series analysis. We also leverage Bayesian mixed models to generate forecasts of future performance and plots of individuals model-implied performance by age and position.

There are four (potential) key components of time series data:

  • seasonality
  • trend
  • cycle
  • irregularity

Seasonality corresponds to fluctuations that occur at fixed and known periods (e.g., time of day, day of week, or month of year) (Hyndman & Athanasopoulos, 2021). A trend represents a long-term change (i.e., increase or decrease) in the series. A cycle reflects one or more rises and falls that are not of a fixed frequency, with durations typically lasting at least two years (Hyndman & Athanasopoulos, 2021). Irregularity is random variation or noise.

25.3 Autoregressive Integrated Moving Average (ARIMA) Models

Hyndman & Athanasopoulos (2021) provide a nice overview of ARIMA models. As noted by Hyndman & Athanasopoulos (2021), ARIMA models aim to describe how a variable is correlated with itself over time (autocorrelation)—i.e., how earlier levels of a variable are correlated with later levels of the same variable. ARIMA models perform best when there is a clear pattern where later values are influenced by earlier values. ARIMA models incorporate autoregression effects, moving average effects, and differencing.

ARIMA models can have various numbers of terms and model complexity. They are specified in the following form: \(\text{ARIMA}(p,d,q)\), where:

  • \(p =\) the number of autoregressive terms
  • \(d =\) the number of differences between consecutive scores (to make the time series stationary by reducing trends and seasonality)
  • \(q =\) the number of moving average terms

ARIMA models assume that the data are stationary (i.e., there are no long-term trends), are non-seasonal (i.e., there is no consistency of the timing of the peaks or troughs in the line), and that earlier values influence later values. This may not strongly be the case in fantasy football, so ARIMA models may not be particularly useful in forecasting fantasy football performance. Other approaches, such as exponential smoothing, may be useful for data that show longer-term trends and seasonality (Hyndman & Athanasopoulos, 2021). Nevertheless, ARIMA models are widely used in forecasting financial markets and economic indicators. Thus, it is a useful technique to learn.

Adapted from: https://rc2e.com/timeseriesanalysis [Long & Teetor (2019); archived at https://perma.cc/U5P6-2VWC].

25.3.1 Create the Time Series Objects

Code
weeklyFantasyPoints_tomBrady <- player_stats_weekly %>% 
  filter(
    player_id == "00-0019596" | player_display_name == "Tom Brady")

weeklyFantasyPoints_peytonManning <- player_stats_weekly %>% 
  filter(
    player_id == "00-0010346" | player_display_name == "Peyton Manning")

ts_tomBrady <- xts::xts(
  x = weeklyFantasyPoints_tomBrady["fantasyPoints"],
  order.by = weeklyFantasyPoints_tomBrady$gameday)

ts_peytonManning <- xts::xts(
  x = weeklyFantasyPoints_peytonManning["fantasyPoints"],
  order.by = weeklyFantasyPoints_peytonManning$gameday)

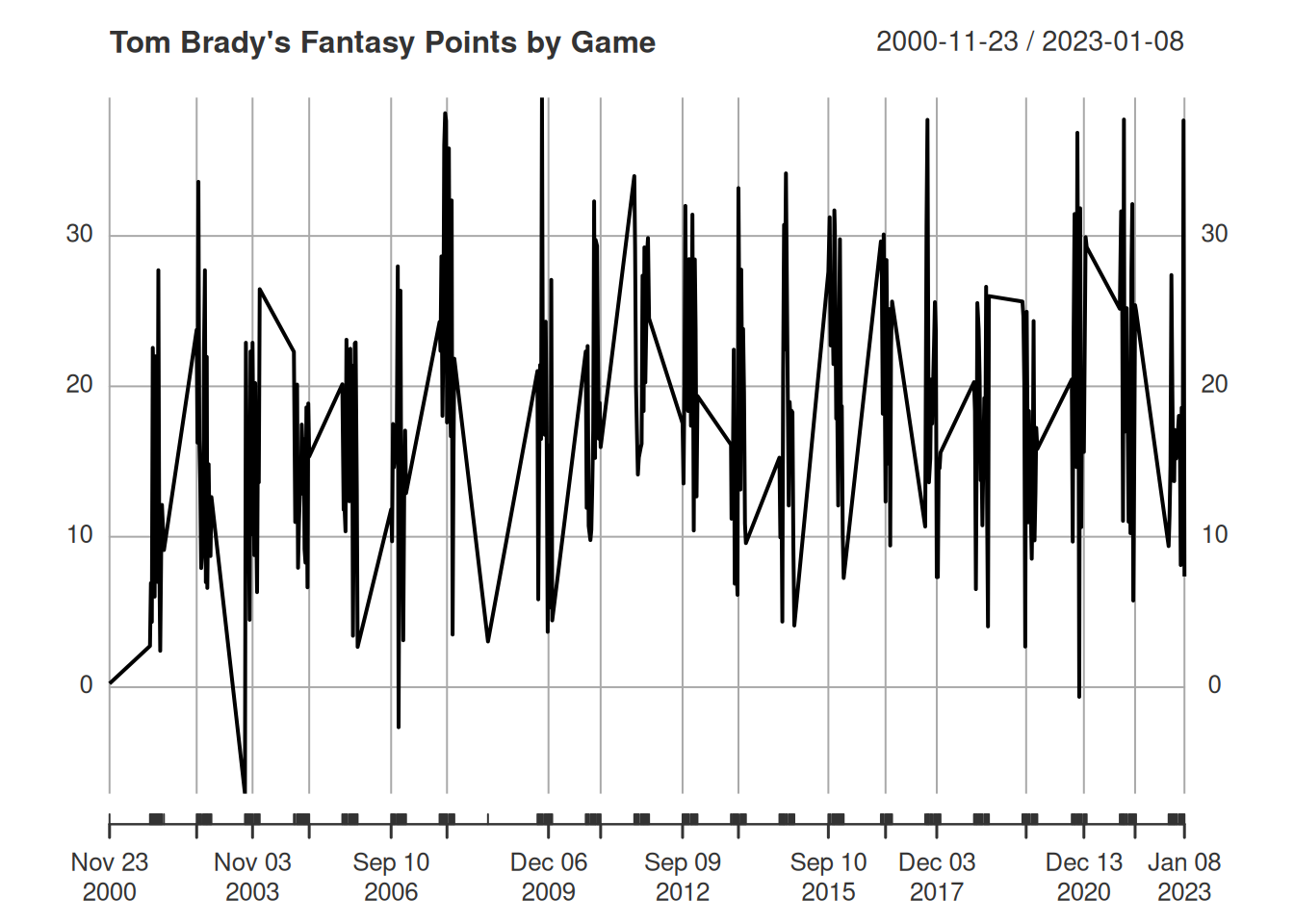
ts_tomBrady
           fantasyPoints
2000-11-23          0.24
2001-09-23          2.74
2001-09-30          6.92
2001-10-07          4.34
2001-10-14         22.56
2001-10-21         19.88
2001-10-28         10.02
2001-11-04         22.00
2001-11-11          8.18
2001-11-18          9.00
       ...              
2022-10-27         17.10
2022-11-06         15.20
2022-11-13         17.02
2022-11-27         18.04
2022-12-05         17.14
2022-12-11         10.12
2022-12-18         20.58
2022-12-25         11.34
2023-01-01         37.68
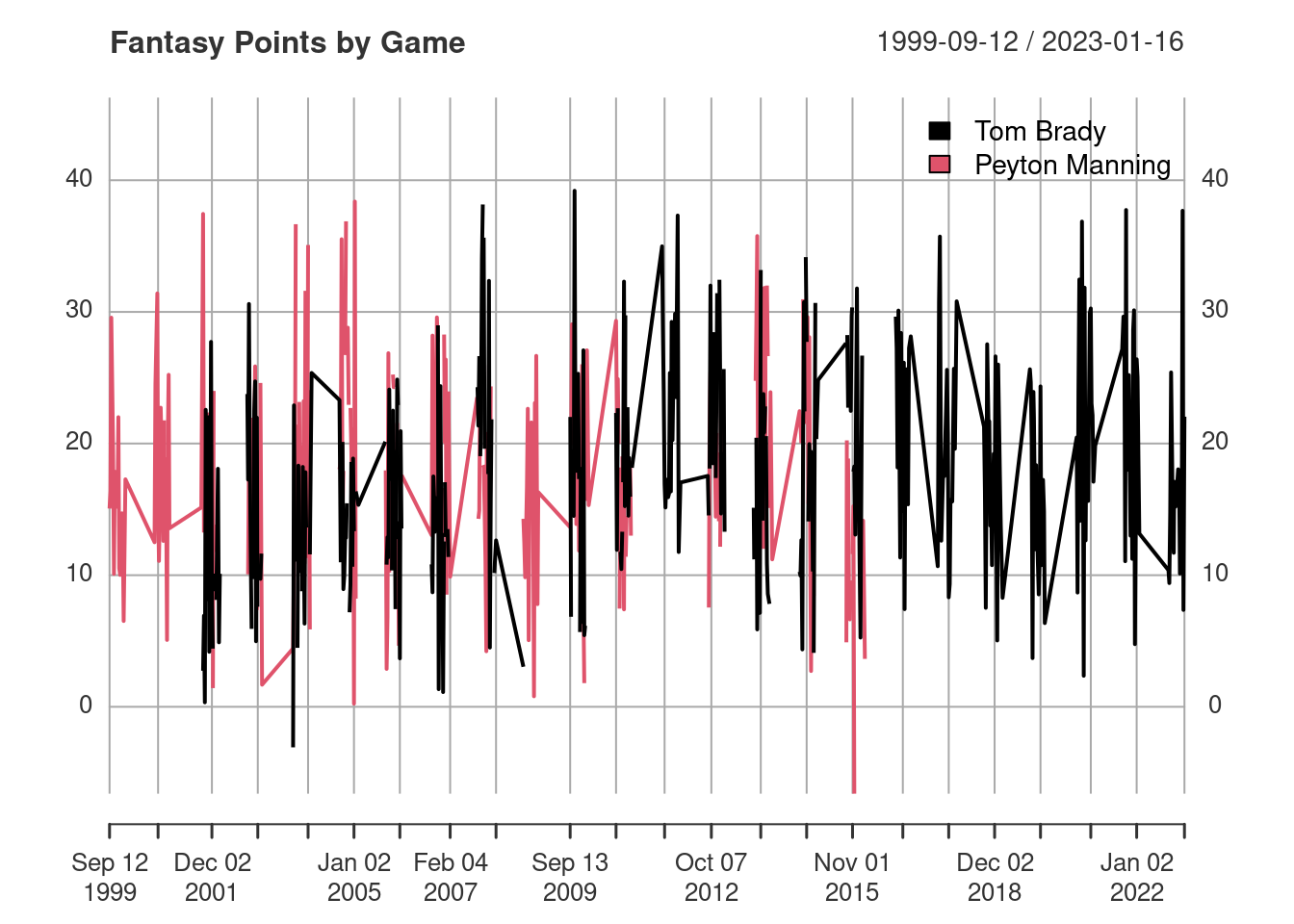
2023-01-08          7.36
Code
ts_peytonManning
           fantasyPoints
1999-09-12         15.06
1999-09-19         17.22
1999-09-26         29.56
1999-10-10         20.66
1999-10-17         10.10
1999-10-24         17.86
1999-10-31         18.52
1999-11-07         20.60
1999-11-14         15.18
1999-11-21         22.80
       ...              
2015-09-13          4.90
2015-09-17         20.24
2015-09-27         18.86
2015-10-04          8.32
2015-10-11          6.64
2015-10-18          9.60
2015-11-01         11.60
2015-11-08         15.24
2015-11-15         -6.60
2016-01-03          2.56
Code
ts_combined <- merge(
  ts_tomBrady,
  ts_peytonManning
)

names(ts_combined) <- c("Tom Brady","Peyton Manning")

25.3.2 Plot the Time Series

Code
plot(
  ts_tomBrady,
  main = "Tom Brady's Fantasy Points by Game")
Tom Brady's Historical Fantasy Points by Game.
Figure 25.1: Tom Brady’s Historical Fantasy Points by Game.
Code
plot(
  ts_combined,
  legend,
  legend.loc = "topright",
  main = "Fantasy Points by Game")
Historical Fantasy Points by Game for Tom Brady and Peyton Manning.
Figure 25.2: Historical Fantasy Points by Game for Tom Brady and Peyton Manning.

25.3.3 Rolling Mean/Median

Code
zoo::rollmean(
  x = ts_tomBrady,
  k = 5)
           fantasyPoints
2001-09-30         7.360
2001-10-07        11.288
2001-10-14        12.744
2001-10-21        15.760
2001-10-28        16.528
2001-11-04        13.816
2001-11-11        15.384
2001-11-18        15.084
2001-11-25        11.568
2001-12-02        11.888
       ...              
2022-10-16        18.332
2022-10-23        15.892
2022-10-27        15.348
2022-11-06        16.212
2022-11-13        16.900
2022-11-27        15.504
2022-12-05        16.580
2022-12-11        15.444
2022-12-18        19.372
2022-12-25        17.416
Code
zoo::rollmedian(
  x = ts_tomBrady,
  k = 5)
           fantasyPoints
2001-09-30          4.34
2001-10-07          6.92
2001-10-14         10.02
2001-10-21         19.88
2001-10-28         19.88
2001-11-04         10.02
2001-11-11         10.02
2001-11-18          9.00
2001-11-25          8.52
2001-12-02          9.00
       ...              
2022-10-16         17.10
2022-10-23         15.20
2022-10-27         15.20
2022-11-06         17.02
2022-11-13         17.10
2022-11-27         17.02
2022-12-05         17.14
2022-12-11         17.14
2022-12-18         17.14
2022-12-25         11.34

25.3.4 Autocorrelation

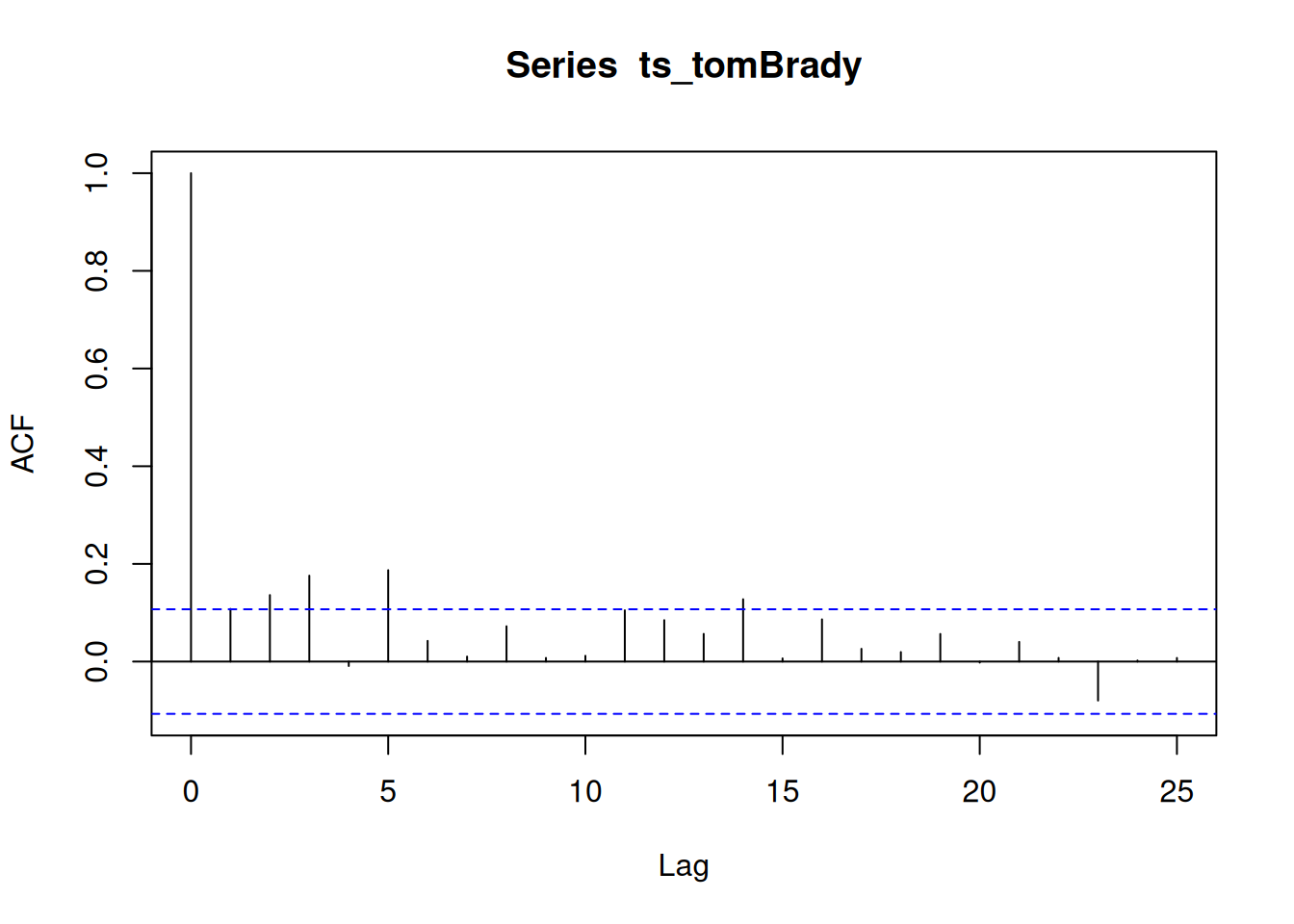
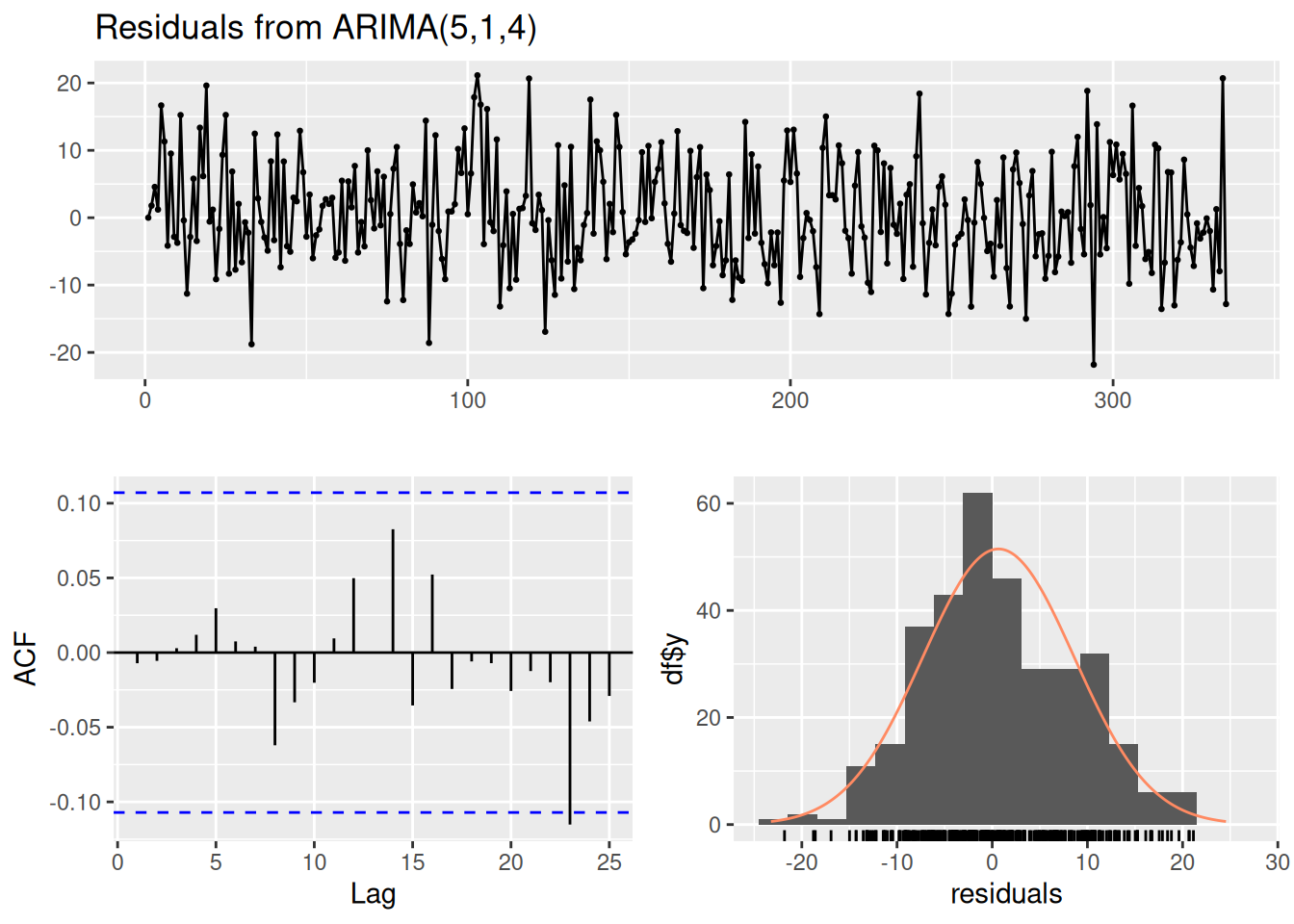
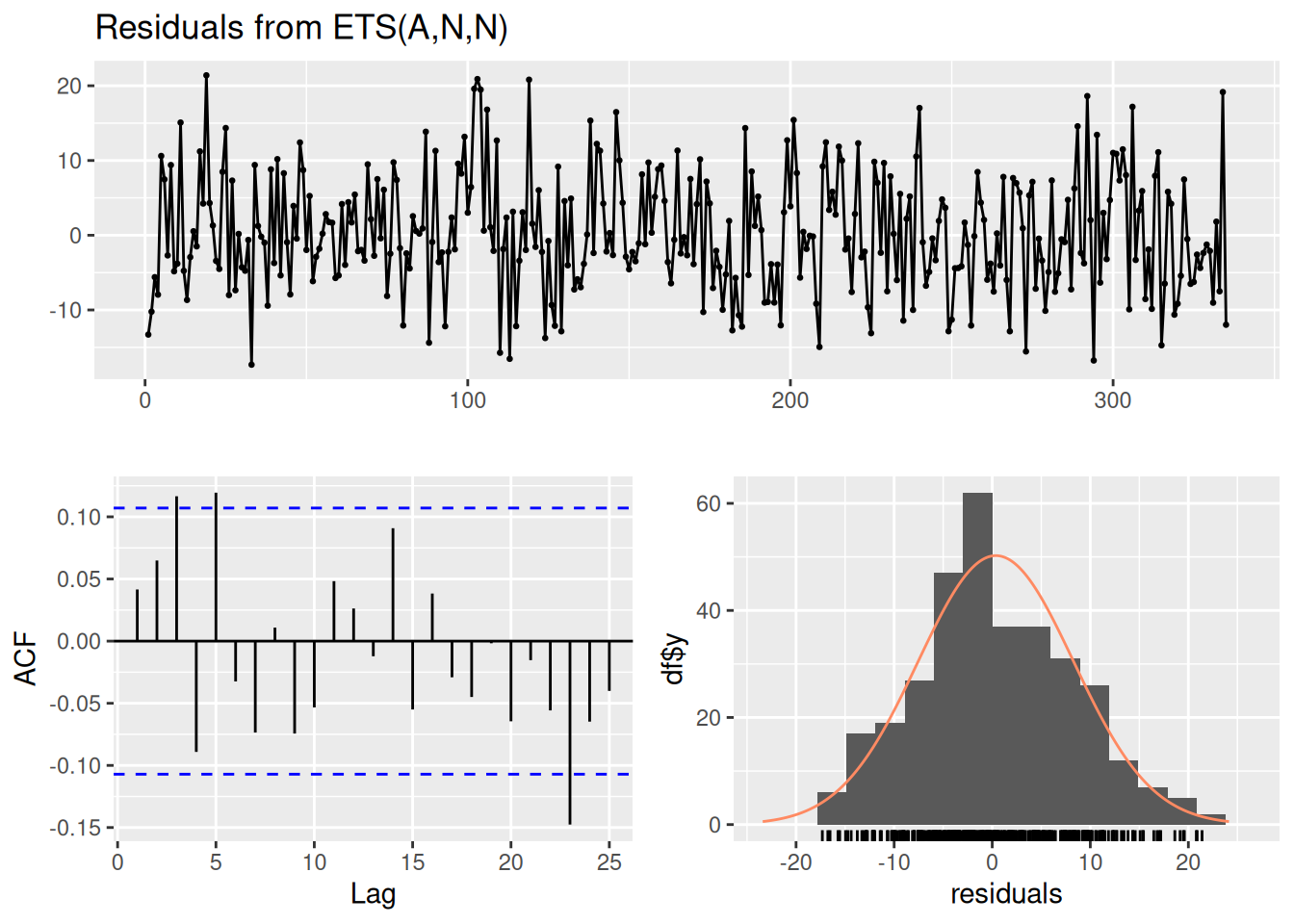
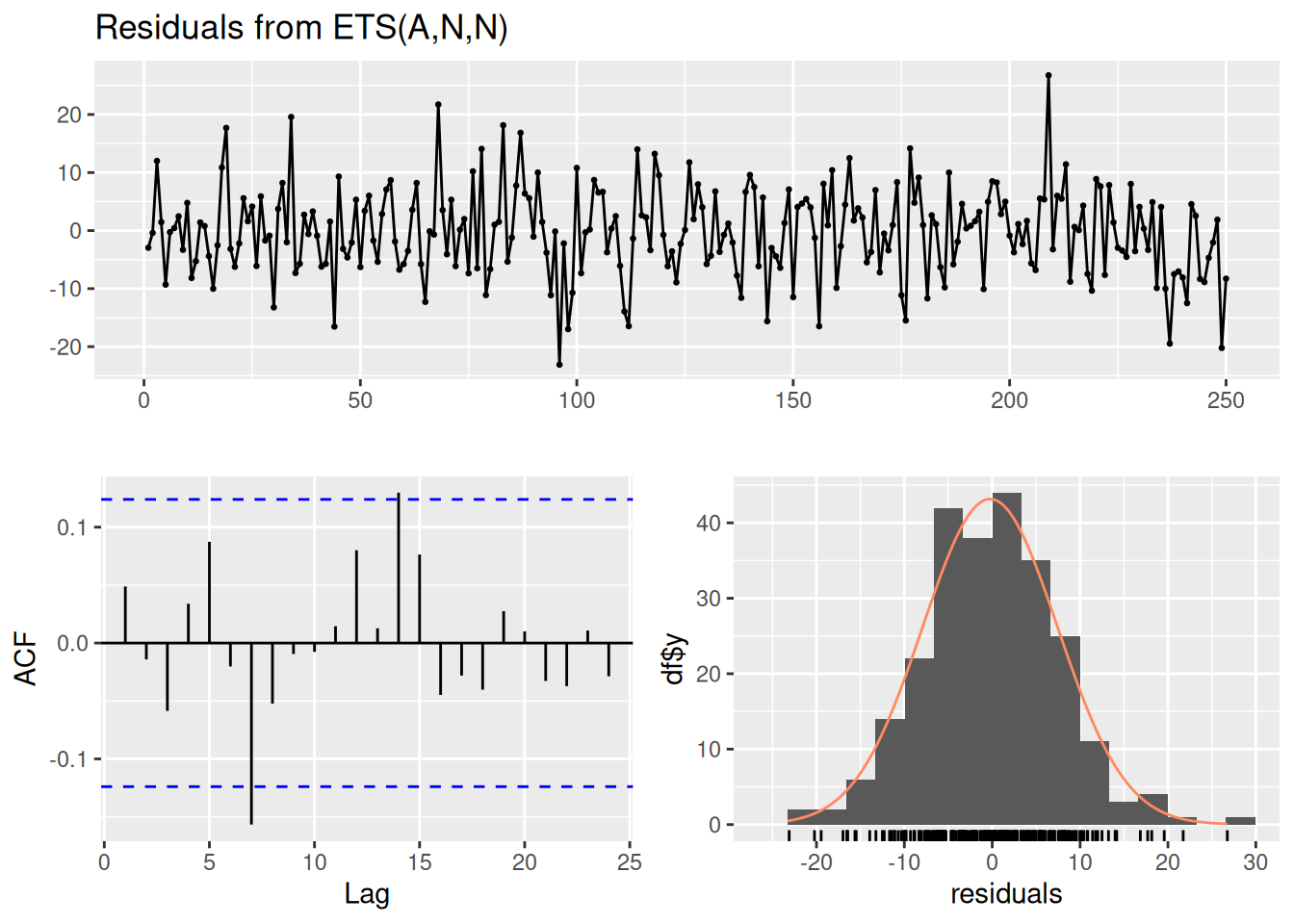
The autocorrelation function (ACF) plot depicts the autocorrelation of scores as a function of the length of the lag. We can generate an ACF plot using the stats::acf() function. Significant autocorrelation is detected when the autocorrelation exceeds the dashed blue lines, as is depicted in Figure 25.3.

Code
acf(ts_tomBrady)
Autocorrelation Function (ACF) Plot of Tom Brady's Historical Fantasy Points by Game.
Figure 25.3: Autocorrelation Function (ACF) Plot of Tom Brady’s Historical Fantasy Points by Game.
Code
Box.test(ts_tomBrady)

    Box-Pierce test

data:  ts_tomBrady
X-squared = 4.6744, df = 1, p-value = 0.03062

25.3.5 Fit an Autoregressive Integrated Moving Average Model

We can fit an ARIMA model using the forecast::auto.arima() function of the forecast package (Hyndman et al., 2024; Hyndman & Khandakar, 2008):

Code
forecast::auto.arima(ts_tomBrady)
Series: ts_tomBrady 
ARIMA(2,1,2) 

Coefficients:
         ar1     ar2      ma1     ma2
      0.5827  0.0703  -1.5041  0.5161
s.e.  0.2615  0.0658   0.2577  0.2496

sigma^2 = 62.76:  log likelihood = -1164.4
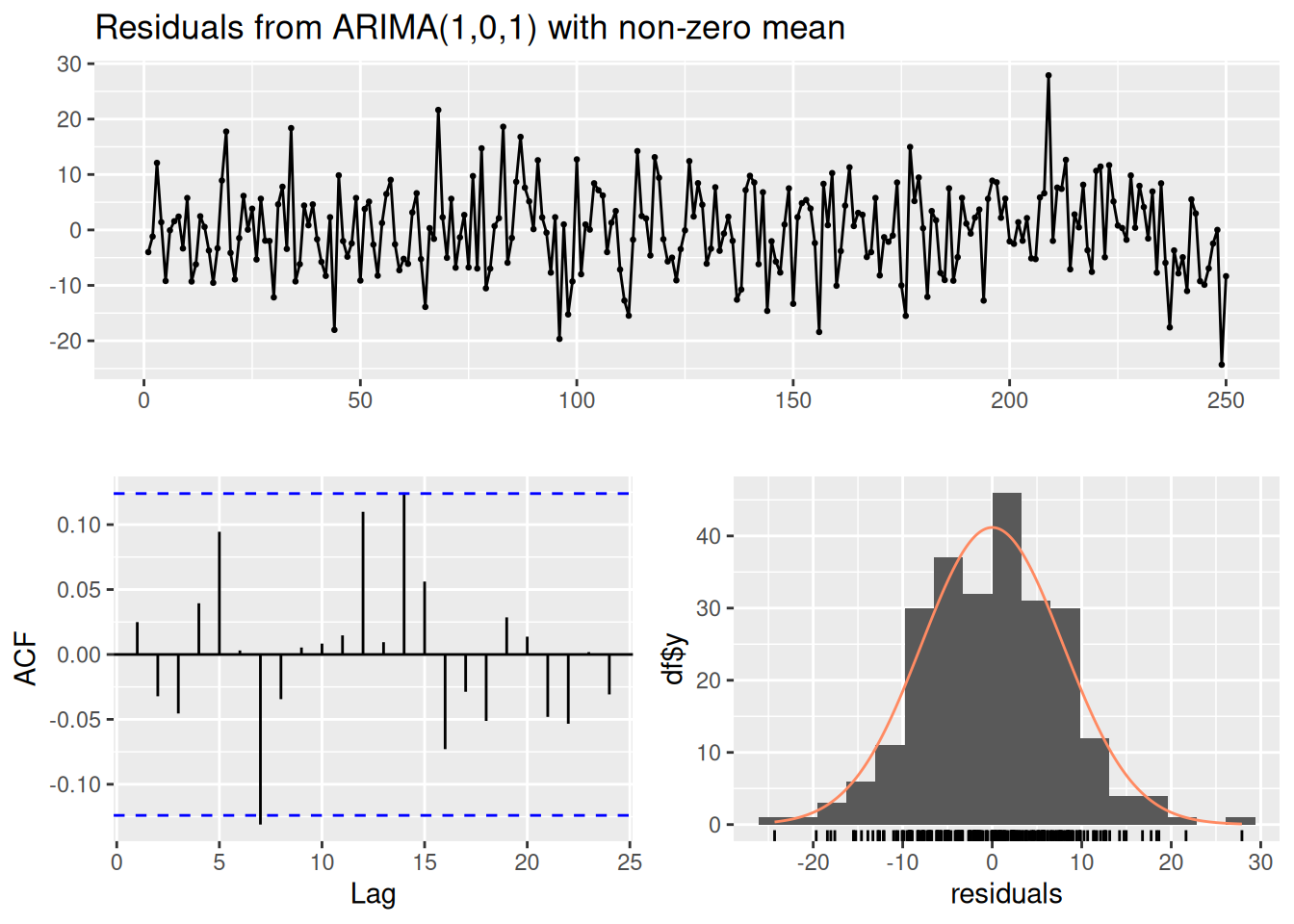
AIC=2338.8   AICc=2338.99   BIC=2357.86
Code
forecast::auto.arima(ts_peytonManning)
Series: ts_peytonManning 
ARIMA(1,0,1) with non-zero mean 

Coefficients:
         ar1      ma1     mean
      0.8659  -0.7311  18.1529
s.e.  0.0973   0.1287   0.9575

sigma^2 = 57.94:  log likelihood = -860.72
AIC=1729.43   AICc=1729.59   BIC=1743.52

We can generate a plot of an ARIMA model using the stats::arima() function.

Code
arima_tomBrady <- arima(
  ts_tomBrady,
  order = c(5, 1, 4))

summary(arima_tomBrady)

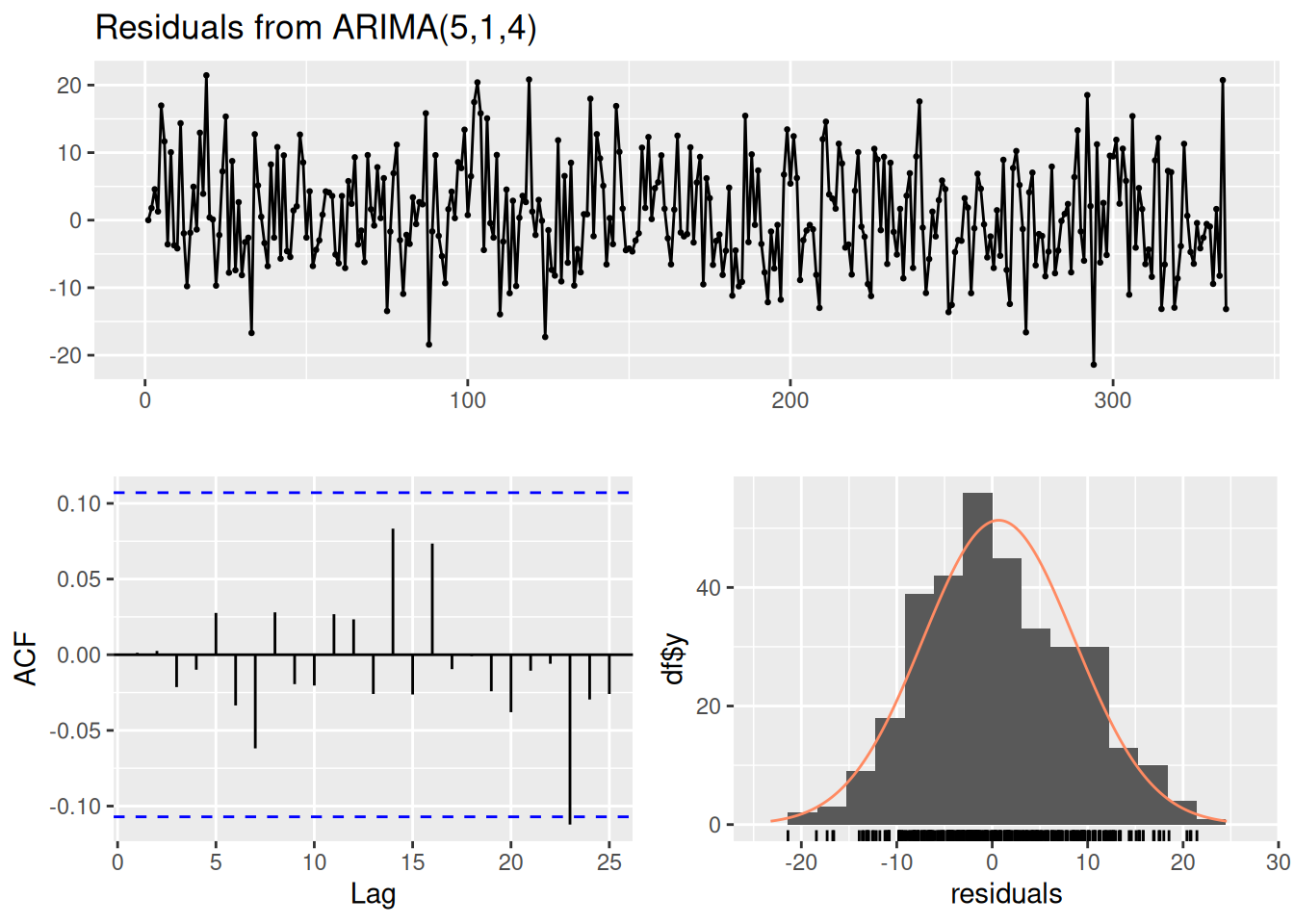
Call:
arima(x = ts_tomBrady, order = c(5, 1, 4))

Coefficients:
         ar1      ar2     ar3      ar4     ar5      ma1     ma2     ma3
      0.3416  -0.0655  -0.205  -0.0959  0.1961  -1.2442  0.3689  0.2403
s.e.     NaN   0.2256     NaN   0.0475  0.0571      NaN     NaN     NaN
          ma4
      -0.3361
s.e.      NaN

sigma^2 estimated as 59.78:  log likelihood = -1158.36,  aic = 2336.72

Training set error measures:
                    ME     RMSE      MAE       MPE     MAPE     MASE
Training set 0.6879023 7.720194 6.223572 -21.21763 50.46479 0.732154
                      ACF1
Training set -0.0007899074
Code
confint(arima_tomBrady)
          2.5 %       97.5 %
ar1         NaN          NaN
ar2 -0.50779428  0.376718457
ar3         NaN          NaN
ar4 -0.18900813 -0.002859993
ar5  0.08427103  0.307929276
ma1         NaN          NaN
ma2         NaN          NaN
ma3         NaN          NaN
ma4         NaN          NaN
Code
forecast::checkresiduals(arima_tomBrady)

    Ljung-Box test

data:  Residuals from ARIMA(5,1,4)
Q* = 4.3247, df = 3, p-value = 0.2285

Model df: 9.   Total lags used: 12
Model Summary of Autoregressive Integrated Moving Average Model fit to Tom Brady's Historical Performance by Game.
Figure 25.4: Model Summary of Autoregressive Integrated Moving Average Model fit to Tom Brady’s Historical Performance by Game.
Code
arima_tomBrady_removeNonSigTerms <- arima(
  ts_tomBrady,
  order = c(5, 1, 4),
  fixed = c(NA, NA, 0, NA, NA, NA, NA, NA, NA))

summary(arima_tomBrady_removeNonSigTerms)

Call:
arima(x = ts_tomBrady, order = c(5, 1, 4), fixed = c(NA, NA, 0, NA, NA, NA, 
    NA, NA, NA))

Coefficients:
          ar1      ar2  ar3     ar4     ar5     ma1      ma2      ma3      ma4
      -0.9051  -0.7933    0  0.0987  0.1551  0.0137  -0.0185  -0.6539  -0.2529
s.e.   0.3144   0.1769    0  0.1013  0.0929  0.3217   0.2181   0.1528   0.1079

sigma^2 estimated as 59.38:  log likelihood = -1157.29,  aic = 2332.58

Training set error measures:
                    ME     RMSE      MAE       MPE     MAPE      MASE
Training set 0.6609654 7.694434 6.168512 -20.93448 50.25172 0.7256766
                     ACF1
Training set -0.006363576
Code
confint(arima_tomBrady_removeNonSigTerms)
          2.5 %      97.5 %
ar1 -1.52137219 -0.28875955
ar2 -1.13999746 -0.44652063
ar3          NA          NA
ar4 -0.09983263  0.29728144
ar5 -0.02703935  0.33727487
ma1 -0.61686843  0.64426701
ma2 -0.44596328  0.40905685
ma3 -0.95344054 -0.35438261
ma4 -0.46435785 -0.04145554
Code
forecast::checkresiduals(arima_tomBrady_removeNonSigTerms)

    Ljung-Box test

data:  Residuals from ARIMA(5,1,4)
Q* = 3.3999, df = 3, p-value = 0.334

Model df: 9.   Total lags used: 12
Model Summary of modified Autoregressive Integrated Moving Average Model fit to Tom Brady's Historical Performance by Game.
Figure 25.5: Model Summary of modified Autoregressive Integrated Moving Average Model fit to Tom Brady’s Historical Performance by Game.
Code
arima_peytonManning <- arima(
  ts_peytonManning,
  order = c(1, 0, 1))

summary(arima_peytonManning)

Call:
arima(x = ts_peytonManning, order = c(1, 0, 1))

Coefficients:
         ar1      ma1  intercept
      0.8659  -0.7311    18.1529
s.e.  0.0973   0.1287     0.9575

sigma^2 estimated as 57.24:  log likelihood = -860.72,  aic = 1729.43

Training set error measures:
                      ME     RMSE      MAE       MPE     MAPE      MASE
Training set 0.002008698 7.565751 5.932631 -101.5589 126.2153 0.7578856
                   ACF1
Training set 0.02467125
Code
confint(arima_peytonManning)
               2.5 %     97.5 %
ar1        0.6752778  1.0565343
ma1       -0.9833206 -0.4789367
intercept 16.2763161 20.0295532
Code
forecast::checkresiduals(arima_peytonManning)

    Ljung-Box test

data:  Residuals from ARIMA(1,0,1) with non-zero mean
Q* = 9.7829, df = 8, p-value = 0.2806

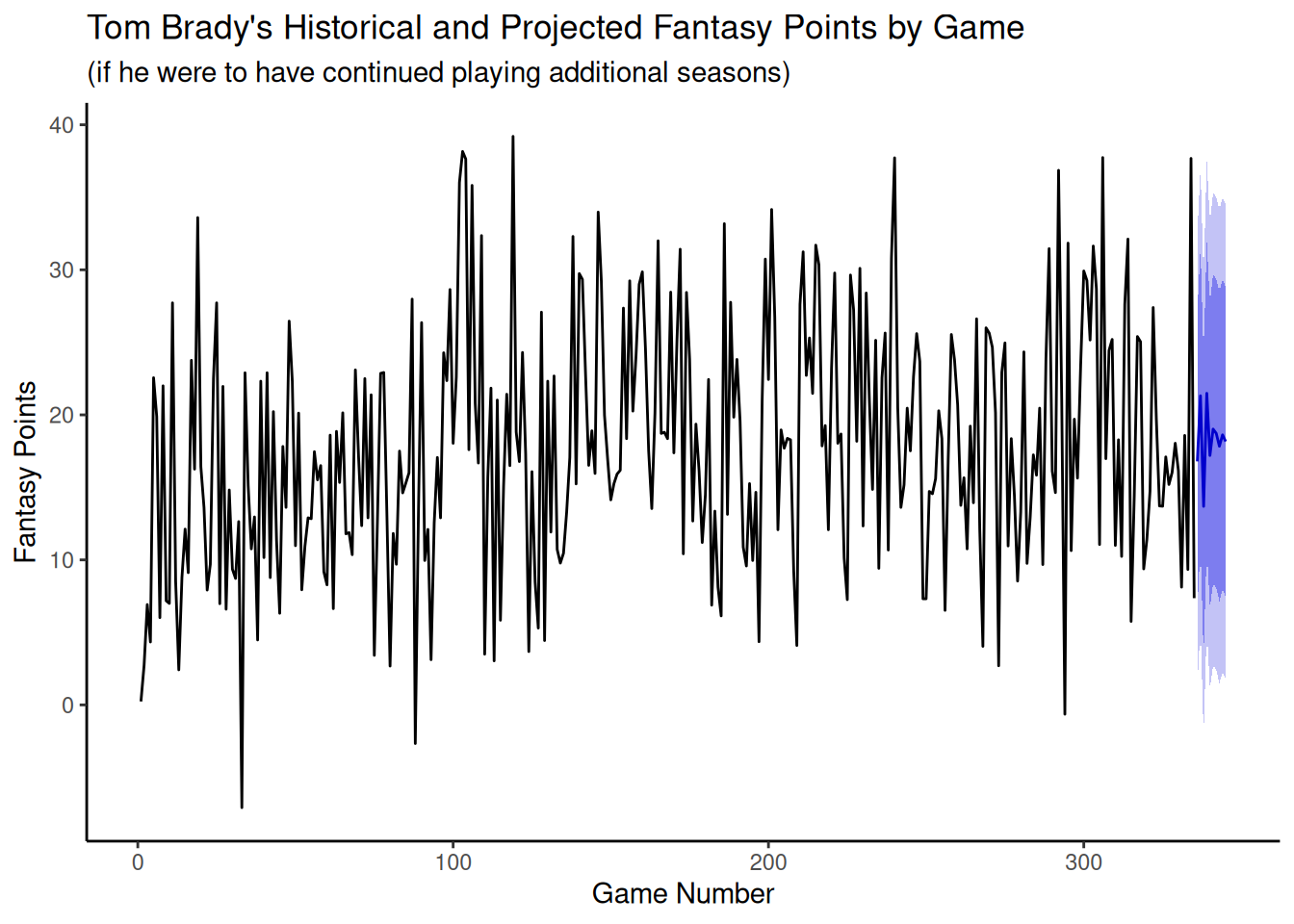
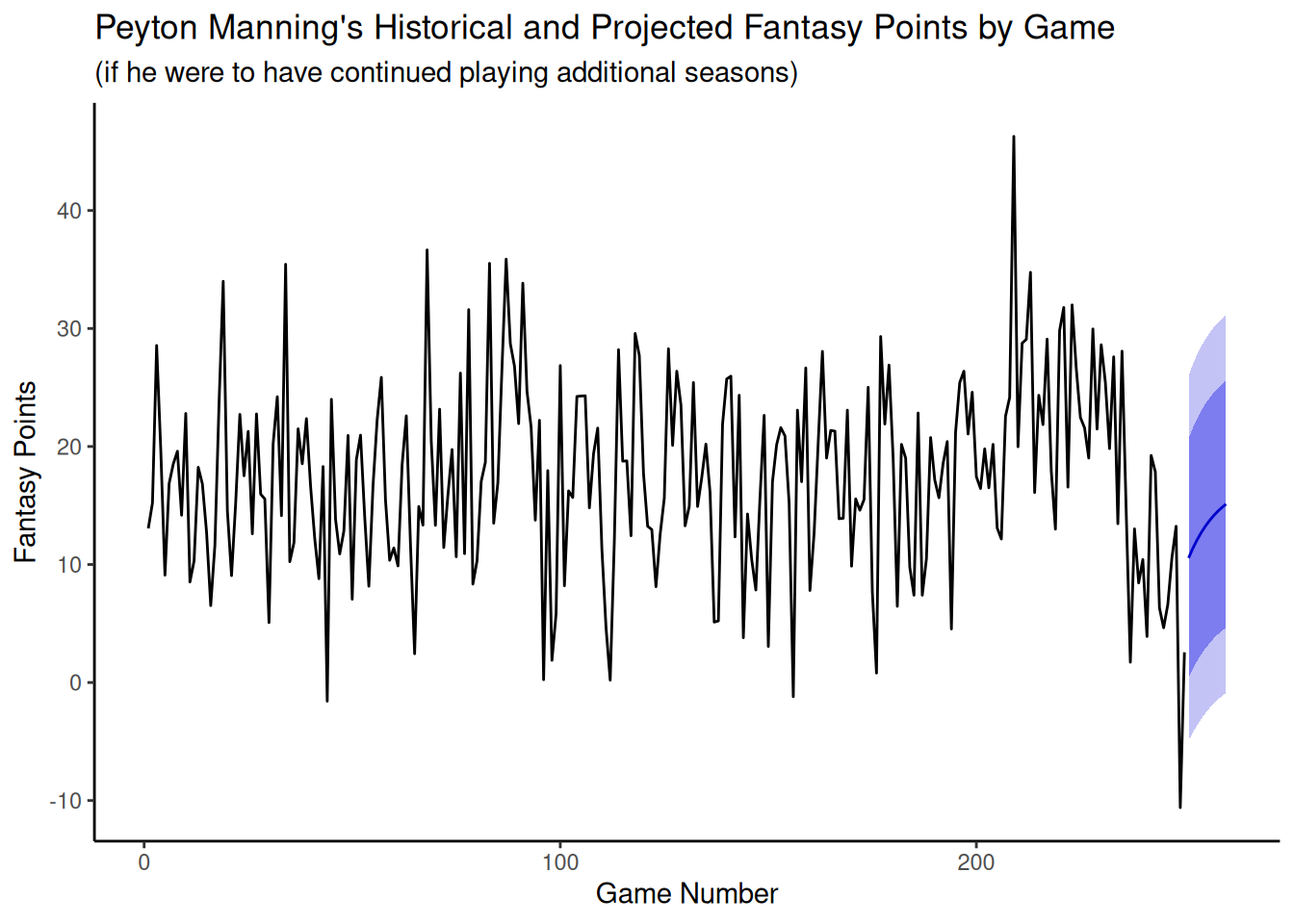
Model df: 2.   Total lags used: 10
Model Summary of Autoregressive Integrated Moving Average Model fit to Peyton Manning's Historical Performance by Game.
Figure 25.6: Model Summary of Autoregressive Integrated Moving Average Model fit to Peyton Manning’s Historical Performance by Game.

25.3.6 Generate the Model Forecasts

We can generate model forecasts from the ARIMA model using the forecast::forecast() function.

Code
forecast_tomBrady <- forecast::forecast(
  arima_tomBrady,
  level = c(80, 95)) # 80% and 95% confidence intervals

forecast_peytonManning <- forecast::forecast(
  arima_peytonManning,
  level = c(80, 95)) # 80% and 95% confidence intervals

forecast_tomBrady
    Point Forecast     Lo 80    Hi 80      Lo 95    Hi 95
336       16.89941  6.990778 26.80803  1.7454680 32.05334
337       21.84148 11.885926 31.79704  6.6157730 37.06719
338       14.62678  4.629175 24.62438 -0.6632356 29.91679
339       22.63793 12.473318 32.80254  7.0924968 38.18336
340       17.97384  7.804932 28.14275  2.4218376 33.52584
341       18.73072  8.416107 29.04533  2.9558825 34.50555
342       19.31420  8.980909 29.64748  3.5107975 35.11759
343       18.23659  7.893548 28.57964  2.4182709 34.05491
344       19.69349  9.341389 30.04559  3.8613185 35.52566
345       19.15502  8.802780 29.50726  3.3226357 34.98740
Code
forecast_peytonManning
    Point Forecast    Lo 80    Hi 80       Lo 95    Hi 95
251       12.03144 2.335537 21.72734 -2.79716238 26.86004
252       12.85229 3.068726 22.63586 -2.11038095 27.81497
253       13.56308 3.714290 23.41186 -1.49934216 28.62550
254       14.17855 4.281143 24.07595 -0.95822712 29.31533
255       14.71149 4.777786 24.64519 -0.48079979 29.90378
256       15.17297 5.212133 25.13380 -0.06081402 30.40675
257       15.57256 5.591435 25.55369  0.30774583 30.83738
258       15.91857 5.922259 25.91489  0.63052902 31.20662
259       16.21819 6.210500 26.22588  0.91274926 31.52363
260       16.47763 6.461418 26.49383  1.15915808 31.79610

25.3.7 Plot the Model Forecasts

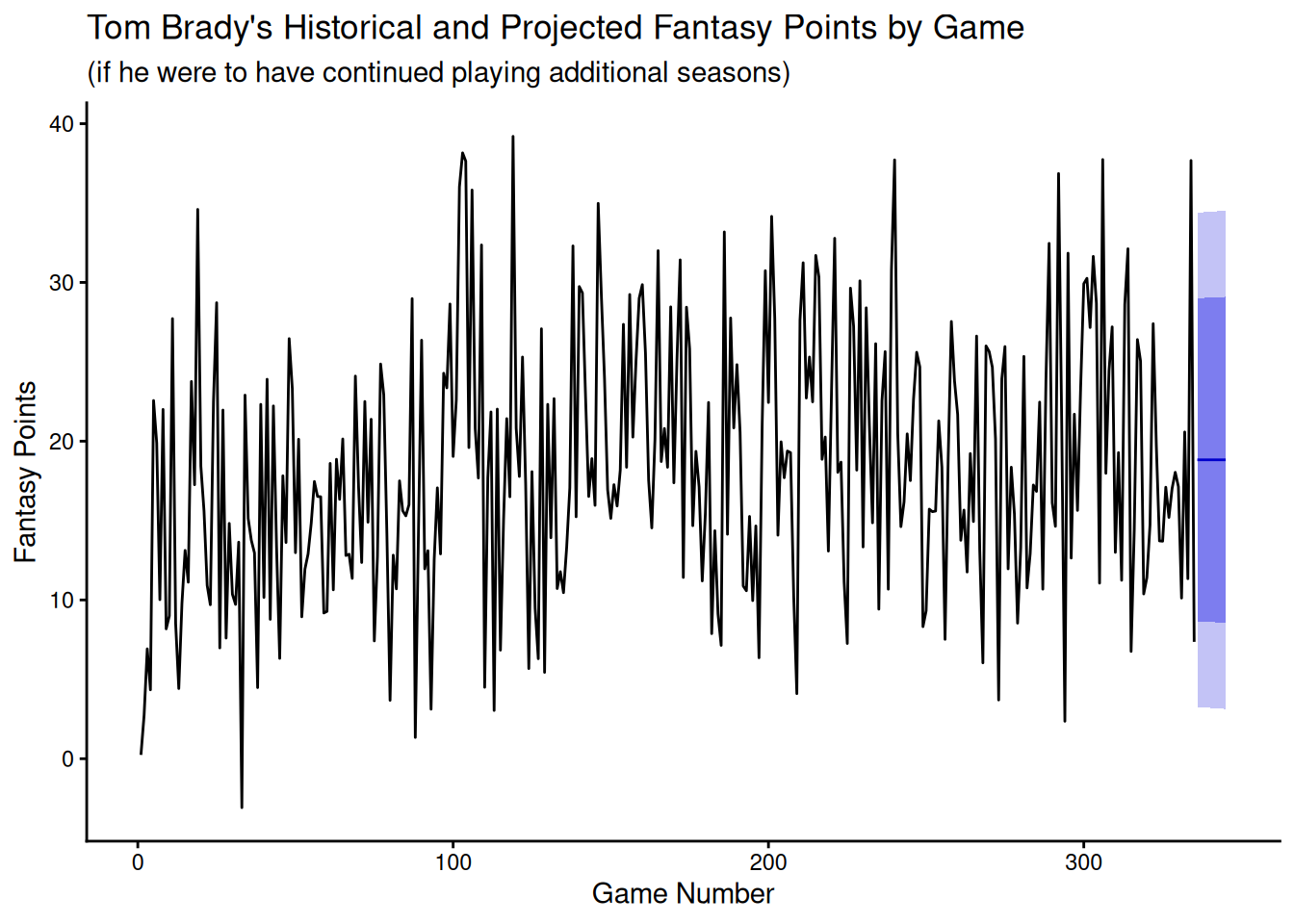
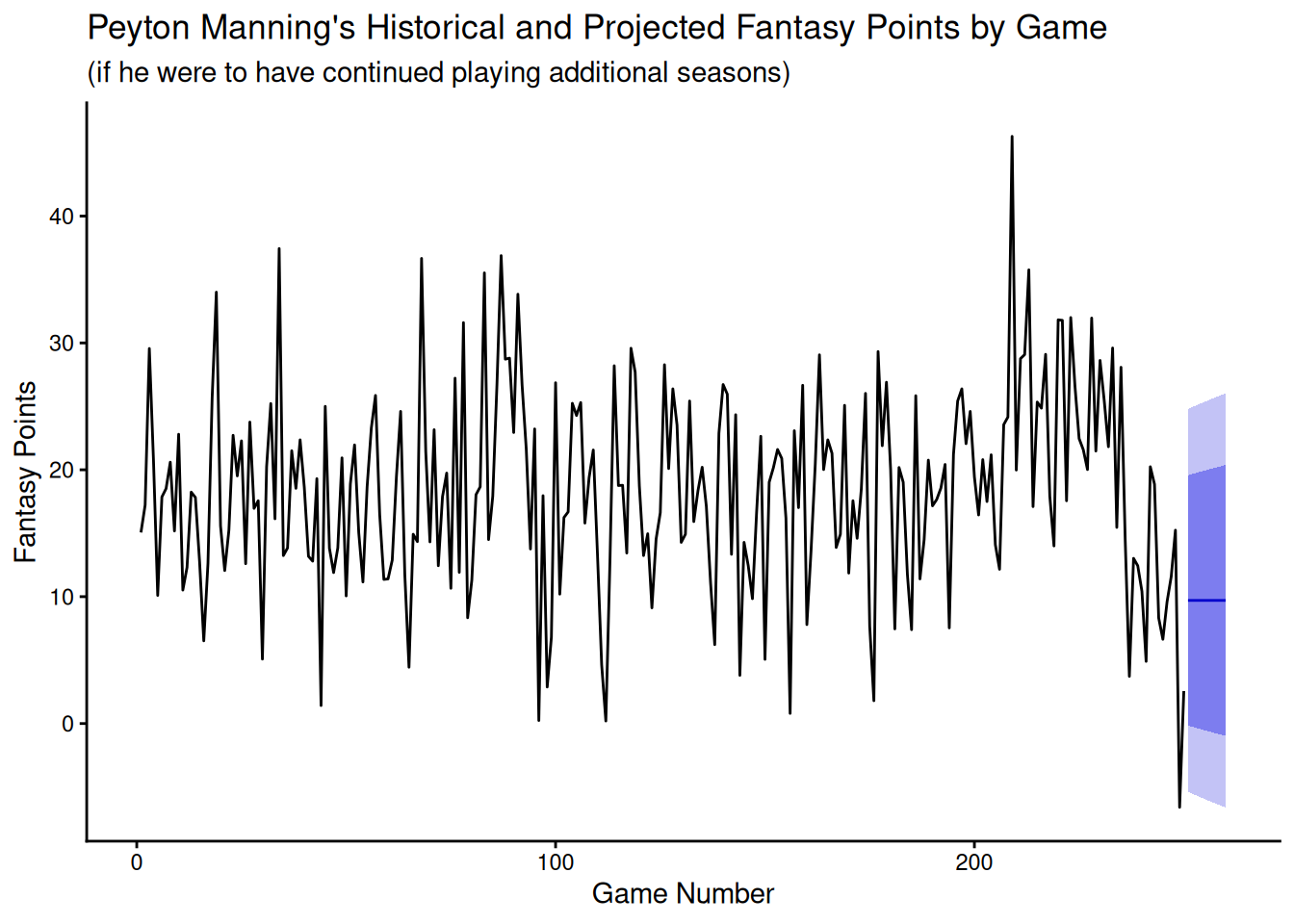
We can plot the model forecasts using the forecast::autoplot() function.

Code
forecast::autoplot(forecast_tomBrady) + 
  labs(
    x = "Game Number",
    y = "Fantasy Points",
    title = "Tom Brady's Historical and Projected Fantasy Points by Game",
    subtitle = "(if he were to have continued playing additional seasons)"
  ) +
  theme_classic()
Tom Brady's Historical and Projected Fantasy Points by Game Based on Autoregressive Integrated Moving Average (ARIMA) Model.
Figure 25.7: Tom Brady’s Historical and Projected Fantasy Points by Game Based on Autoregressive Integrated Moving Average (ARIMA) Model.
Code
forecast::autoplot(forecast_peytonManning) + 
  labs(
    x = "Game Number",
    y = "Fantasy Points",
    title = "Peyton Manning's Historical and Projected Fantasy Points by Game",
    subtitle = "(if he were to have continued playing additional seasons)"
  ) +
  theme_classic()
Peyton Manning's Historical and Projected Fantasy Points by Game Based on Autoregressive Integrated Moving Average (ARIMA) Model.
Figure 25.8: Peyton Manning’s Historical and Projected Fantasy Points by Game Based on Autoregressive Integrated Moving Average (ARIMA) Model.

25.4 Exponential Smoothing

25.4.1 Fit the Exponential Smoothing Model

We fit exponential smoothing models using the forecast::ets() function of the forecast package (Hyndman et al., 2024; Hyndman & Khandakar, 2008):

Code
ets_tomBrady <- forecast::ets(ts_tomBrady)
ets_peytonManning <- forecast::ets(ts_peytonManning)

We can generate a plot of an ARIMA model using the stats::arima() function.

Code
summary(ets_tomBrady)
ETS(A,N,N) 

Call:
forecast::ets(y = ts_tomBrady)

  Smoothing parameters:
    alpha = 0.0426 

  Initial states:
    l = 13.5319 

  sigma:  7.9439

     AIC     AICc      BIC 
3340.243 3340.315 3351.685 

Training set error measures:
                    ME   RMSE      MAE     MPE     MAPE      MASE       ACF1
Training set 0.3709126 7.9202 6.376596 -42.104 70.03779 0.7501561 0.04152263
Code
forecast::checkresiduals(ets_tomBrady)

    Ljung-Box test

data:  Residuals from ETS(A,N,N)
Q* = 19.391, df = 10, p-value = 0.03557

Model df: 0.   Total lags used: 10
Model Summary of Exponential Smoothing Model fit to Tom Brady's Historical Performance by Game.
Figure 25.9: Model Summary of Exponential Smoothing Model fit to Tom Brady’s Historical Performance by Game.
Code
summary(ets_peytonManning)
ETS(A,N,N) 

Call:
forecast::ets(y = ts_peytonManning)

  Smoothing parameters:
    alpha = 0.1375 

  Initial states:
    l = 18.0175 

  sigma:  7.7031

     AIC     AICc      BIC 
2405.168 2405.266 2415.733 

Training set error measures:
                     ME     RMSE      MAE       MPE     MAPE     MASE
Training set -0.2418607 7.672223 6.032439 -107.9247 132.1507 0.770636
                   ACF1
Training set 0.04883502
Code
forecast::checkresiduals(ets_peytonManning)

    Ljung-Box test

data:  Residuals from ETS(A,N,N)
Q* = 11.003, df = 10, p-value = 0.3573

Model df: 0.   Total lags used: 10
Model Summary of Exponential Smoothing Model fit to Peyton Manning's Historical Performance by Game.
Figure 25.10: Model Summary of Exponential Smoothing Model fit to Peyton Manning’s Historical Performance by Game.

25.4.2 Generate the Model Forecasts

We can generate model forecasts from the ARIMA model using the forecast::forecast() function.

Code
forecastETS_tomBrady <- forecast::forecast(
  ets_tomBrady,
  level = c(80, 95)) # 80% and 95% confidence intervals

forecastETS_peytonManning <- forecast::forecast(
  ets_peytonManning,
  level = c(80, 95)) # 80% and 95% confidence intervals

forecastETS_tomBrady
    Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
336       18.82671 8.646134 29.00729 3.256861 34.39657
337       18.82671 8.636896 29.01653 3.242732 34.41070
338       18.82671 8.627666 29.02576 3.228615 34.42481
339       18.82671 8.618444 29.03499 3.214512 34.43892
340       18.82671 8.609230 29.04420 3.200421 34.45301
341       18.82671 8.600025 29.05340 3.186342 34.46709
342       18.82671 8.590828 29.06260 3.172277 34.48115
343       18.82671 8.581639 29.07179 3.158224 34.49521
344       18.82671 8.572459 29.08097 3.144183 34.50925
345       18.82671 8.563286 29.09014 3.130156 34.52327
Code
forecastETS_peytonManning
    Point Forecast      Lo 80    Hi 80     Lo 95    Hi 95
251       9.705069 -0.1668464 19.57699 -5.392723 24.80286
252       9.705069 -0.2596969 19.66984 -5.534726 24.94486
253       9.705069 -0.3516901 19.76183 -5.675417 25.08556
254       9.705069 -0.4428494 19.85299 -5.814833 25.22497
255       9.705069 -0.5331971 19.94334 -5.953008 25.36315
256       9.705069 -0.6227545 20.03289 -6.089974 25.50011
257       9.705069 -0.7115419 20.12168 -6.225763 25.63590
258       9.705069 -0.7995789 20.20972 -6.360404 25.77054
259       9.705069 -0.8868841 20.29702 -6.493926 25.90406
260       9.705069 -0.9734757 20.38361 -6.626356 26.03649

25.4.3 Plot the Model Forecasts

We can plot the model forecasts using the forecast::autoplot() function.

Code
forecast::autoplot(forecastETS_tomBrady) + 
  labs(
    x = "Game Number",
    y = "Fantasy Points",
    title = "Tom Brady's Historical and Projected Fantasy Points by Game",
    subtitle = "(if he were to have continued playing additional seasons)"
  ) +
  theme_classic()
Tom Brady's Historical and Projected Fantasy Points by Game Based on Exponential Smoothing.
Figure 25.11: Tom Brady’s Historical and Projected Fantasy Points by Game Based on Exponential Smoothing.
Code
forecast::autoplot(forecastETS_peytonManning) + 
  labs(
    x = "Game Number",
    y = "Fantasy Points",
    title = "Peyton Manning's Historical and Projected Fantasy Points by Game",
    subtitle = "(if he were to have continued playing additional seasons)"
  ) +
  theme_classic()
Peyton Manning's Historical and Projected Fantasy Points by Game Based on Exponential Smoothing.
Figure 25.12: Peyton Manning’s Historical and Projected Fantasy Points by Game Based on Exponential Smoothing.

25.5 Bayesian Mixed Models

The Bayesian longitudinal mixed models were estimated in Section 12.4.5.

25.5.1 Prepare New Data Object

Code
player_stats_seasonal_offense_subset <- player_stats_seasonal %>% 
  dplyr::filter(position_group %in% c("QB","RB","WR","TE") | position %in% c("K"))

player_stats_seasonal_offense_subset$position[which(player_stats_seasonal_offense_subset$position == "HB")] <- "RB"

player_stats_seasonal_offense_subset$player_idFactor <- factor(player_stats_seasonal_offense_subset$player_id)
player_stats_seasonal_offense_subset$positionFactor <- factor(player_stats_seasonal_offense_subset$position)
Code
player_stats_seasonal_offense_subsetCC <- player_stats_seasonal_offense_subset %>%
  filter(
    !is.na(player_idFactor),
    !is.na(fantasyPoints),
    !is.na(positionFactor),
    !is.na(ageCentered20),
    !is.na(ageCentered20Quadratic),
    !is.na(years_of_experience))

player_stats_seasonal_offense_subsetCC <- player_stats_seasonal_offense_subsetCC %>% 
  filter(player_id %in% bayesianMixedModelFit$data$player_idFactor) %>% 
  mutate(positionFactor = droplevels(positionFactor))

player_stats_seasonal_offense_subsetCC <- player_stats_seasonal_offense_subsetCC %>%
  group_by(player_id) %>% 
  group_modify(~ add_row(.x, season = max(player_stats_seasonal_offense_subsetCC$season) + 1)) %>% 
  fill(player_display_name, player_idFactor, position, position_group, positionFactor, team, .direction = "downup") %>% 
  ungroup

player_stats_seasonal_offense_subsetCC <- player_stats_seasonal_offense_subsetCC %>% 
  left_join(
    player_stats_seasonal_offense_subsetCC %>% 
      filter(season == max(player_stats_seasonal_offense_subsetCC$season) - 1) %>% 
      select(player_id, age_lastYear = age, years_of_experience_lastYear = years_of_experience),
    by = "player_id") %>%
  mutate(
    age = if_else(season == max(player_stats_seasonal_offense_subsetCC$season), age_lastYear + 1, age), # increment age by 1
    ageCentered20 = age - 20,
    years_of_experience = if_else(season == max(player_stats_seasonal_offense_subsetCC$season), years_of_experience_lastYear + 1, years_of_experience)) # increment experience by 1

activePlayers <- unique(player_stats_seasonal_offense_subsetCC[c("player_id","season")]) %>% 
  filter(season == max(player_stats_seasonal_offense_subsetCC$season) - 1) %>% 
  select(player_id) %>% 
  pull()

inactivePlayers <- player_stats_seasonal_offense_subsetCC$player_id[which(player_stats_seasonal_offense_subsetCC$player_id %ni% activePlayers)]

player_stats_seasonal_offense_subsetCC <- player_stats_seasonal_offense_subsetCC %>% 
  filter(player_id %in% activePlayers | (player_id %in% inactivePlayers & season < max(player_stats_seasonal_offense_subsetCC$season) - 1)) %>% 
  mutate(
    player_idFactor = droplevels(player_idFactor) 
  )

25.5.2 Generate Predictions

Code
player_stats_seasonal_offense_subsetCC$fantasyPoints_bayesian <- predict(
  bayesianMixedModelFit,
  newdata = player_stats_seasonal_offense_subsetCC
)[,"Estimate"]

25.5.3 Table of Next Season Predictions

Code
player_stats_seasonal_offense_subsetCC %>% 
  filter(season == max(player_stats_seasonal_offense_subsetCC$season), position == "QB") %>%
  arrange(-fantasyPoints_bayesian) %>% 
  select(player_display_name, fantasyPoints_bayesian)
Code
player_stats_seasonal_offense_subsetCC %>% 
  filter(season == max(player_stats_seasonal_offense_subsetCC$season), position == "RB") %>%
  arrange(-fantasyPoints_bayesian) %>% 
  select(player_display_name, fantasyPoints_bayesian)
Code
player_stats_seasonal_offense_subsetCC %>% 
  filter(season == max(player_stats_seasonal_offense_subsetCC$season), position == "WR") %>%
  arrange(-fantasyPoints_bayesian) %>% 
  select(player_display_name, fantasyPoints_bayesian)
Code
player_stats_seasonal_offense_subsetCC %>% 
  filter(season == max(player_stats_seasonal_offense_subsetCC$season), position == "TE") %>%
  arrange(-fantasyPoints_bayesian) %>% 
  select(player_display_name, fantasyPoints_bayesian)

25.5.4 Plot of Individuals’ Model-Implied Predictions

25.5.4.1 Quarterbacks

Code
plot_individualFantasyPointsByAgeQB <- ggplot(
  data = player_stats_seasonal_offense_subsetCC %>% filter(position == "QB"),
  mapping = aes(
    x = round(age, 2),
    y = round(fantasyPoints_bayesian, 2),
    group = player_id)) +
  geom_smooth(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    se = FALSE,
    linewidth = 0.5,
    color = "black") +
  geom_point(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    size = 1,
    color = "transparent" # make points invisible but keep tooltips
  ) +
  labs(
    x = "Player Age (years)",
    y = "Fantasy Points (Season)",
    title = "Fantasy Points (Season) by Player Age: Quarterbacks"
  ) +
  theme_classic()

plotly::ggplotly(
  plot_individualFantasyPointsByAgeQB,
  tooltip = c("age","fantasyPoints_bayesian","text","label")
)
Figure 25.13: Plot of Individuals’ Implied Trajectories of Fantasy Points by Age, from a Bayesian Generalized Additive Model, for Quarterbacks.

25.5.4.2 Running Backs

Code
plot_individualFantasyPointsByAgeRB <- ggplot(
  data = player_stats_seasonal_offense_subsetCC %>% filter(position == "RB"),
  mapping = aes(
    x = age,
    y = fantasyPoints_bayesian,
    group = player_id)) +
  geom_smooth(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    se = FALSE,
    linewidth = 0.5,
    color = "black") +
  geom_point(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    size = 1,
    color = "transparent" # make points invisible but keep tooltips
  ) +
  labs(
    x = "Player Age (years)",
    y = "Fantasy Points (Season)",
    title = "Fantasy Points (Season) by Player Age: Running Backs"
  ) +
  theme_classic()

plotly::ggplotly(
  plot_individualFantasyPointsByAgeRB,
  tooltip = c("age","fantasyPoints_bayesian","text","label")
)
Figure 25.14: Plot of Individuals’ Implied Trajectories of Fantasy Points by Age, from a Bayesian Generalized Additive Model, for Running Backs.

25.5.4.3 Wide Receivers

Code
plot_individualFantasyPointsByAgeWR <- ggplot(
  data = player_stats_seasonal_offense_subsetCC %>% filter(position == "WR"),
  mapping = aes(
    x = age,
    y = fantasyPoints_bayesian,
    group = player_id)) +
  geom_smooth(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    se = FALSE,
    linewidth = 0.5,
    color = "black") +
  geom_point(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    size = 1,
    color = "transparent" # make points invisible but keep tooltips
  ) +
  labs(
    x = "Player Age (years)",
    y = "Fantasy Points (Season)",
    title = "Fantasy Points (Season) by Player Age: Wide Receivers"
  ) +
  theme_classic()

plotly::ggplotly(
  plot_individualFantasyPointsByAgeWR,
  tooltip = c("age","fantasyPoints_bayesian","text","label")
)
Figure 25.15: Plot of Individuals’ Implied Trajectories of Fantasy Points by Age, from a Bayesian Generalized Additive Model, for Wide Receivers.

25.5.4.4 Tight Ends

Code
plot_individualFantasyPointsByAgeTE <- ggplot(
  data = player_stats_seasonal_offense_subsetCC %>% filter(position == "TE"),
  mapping = aes(
    x = age,
    y = fantasyPoints_bayesian,
    group = player_id)) +
  geom_smooth(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    se = FALSE,
    linewidth = 0.5,
    color = "black") +
  geom_point(
    aes(
      x = age,
      y = fantasyPoints_bayesian,
      text = player_display_name, # add player name for mouse over tooltip
      label = season # add season for mouse over tooltip
    ),
    size = 1,
    color = "transparent" # make points invisible but keep tooltips
  ) +
  labs(
    x = "Player Age (years)",
    y = "Fantasy Points (Season)",
    title = "Fantasy Points (Season) by Player Age: Tight Ends"
  ) +
  theme_classic()

plotly::ggplotly(
  plot_individualFantasyPointsByAgeTE,
  tooltip = c("age","fantasyPoints_bayesian","text","label")
)
Figure 25.16: Plot of Individuals’ Implied Trajectories of Fantasy Points by Age, from a Bayesian Generalized Additive Model, for Tight Ends.

25.6 Conclusion

That is, time series analysis seeks to evaluate change over time to predict future values. There many different types of time series analyses. We demonstrated use of autoregressive integrated moving average (ARIMA) models to predict future fantasy points. ARIMA models aim to describe how how earlier levels of a variable are correlated with later levels of the same variable. ARIMA models perform best when there is a clear pattern where later values are influenced by earlier values. ARIMA models assume that the data are stationary (i.e., there are no long-term trends), are non-seasonal (i.e., there is no consistency of the timing of the peaks or troughs in the line), and that earlier values influence later values. This may not strongly be the case in fantasy football, so ARIMA models may not be particularly useful in forecasting fantasy football performance. We also used Bayesian mixed models to generate forecasts of future performance and plots of individuals model-implied performance by age and position.

25.7 Session Info

Code
sessionInfo()
R version 4.5.2 (2025-10-31)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.3 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
 [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
 [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
[10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   

time zone: UTC
tzcode source: system (glibc)

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] lubridate_1.9.4     forcats_1.0.1       stringr_1.6.0      
 [4] dplyr_1.1.4         purrr_1.2.0         readr_2.1.6        
 [7] tidyr_1.3.1         tibble_3.3.0        tidyverse_2.0.0    
[10] plotly_4.11.0       ggplot2_4.0.1       rstan_2.32.7       
[13] StanHeaders_2.32.10 brms_2.23.0         Rcpp_1.1.0         
[16] forecast_8.24.0     xts_0.14.1          zoo_1.8-14         
[19] petersenlab_1.2.1  

loaded via a namespace (and not attached):
  [1] RColorBrewer_1.1-3    tensorA_0.36.2.1      rstudioapi_0.17.1    
  [4] jsonlite_2.0.0        magrittr_2.0.4        TH.data_1.1-5        
  [7] estimability_1.5.1    farver_2.1.2          nloptr_2.2.1         
 [10] rmarkdown_2.30        vctrs_0.6.5           minqa_1.2.8          
 [13] base64enc_0.1-3       htmltools_0.5.8.1     distributional_0.5.0 
 [16] curl_7.0.0            Formula_1.2-5         TTR_0.24.4           
 [19] htmlwidgets_1.6.4     plyr_1.8.9            sandwich_3.1-1       
 [22] emmeans_2.0.0         lifecycle_1.0.4       pkgconfig_2.0.3      
 [25] Matrix_1.7-4          R6_2.6.1              fastmap_1.2.0        
 [28] rbibutils_2.4         digest_0.6.39         colorspace_2.1-2     
 [31] ps_1.9.1              crosstalk_1.2.2       Hmisc_5.2-4          
 [34] labeling_0.4.3        timechange_0.3.0      mgcv_1.9-3           
 [37] httr_1.4.7            abind_1.4-8           compiler_4.5.2       
 [40] withr_3.0.2           htmlTable_2.4.3       S7_0.2.1             
 [43] backports_1.5.0       tseries_0.10-58       inline_0.3.21        
 [46] DBI_1.2.3             psych_2.5.6           QuickJSR_1.8.1       
 [49] pkgbuild_1.4.8        MASS_7.3-65           loo_2.8.0            
 [52] tools_4.5.2           pbivnorm_0.6.0        foreign_0.8-90       
 [55] lmtest_0.9-40         quantmod_0.4.28       nnet_7.3-20          
 [58] glue_1.8.0            quadprog_1.5-8        nlme_3.1-168         
 [61] grid_4.5.2            cmdstanr_0.9.0.9000   checkmate_2.3.3      
 [64] cluster_2.1.8.1       reshape2_1.4.5        generics_0.1.4       
 [67] gtable_0.3.6          tzdb_0.5.0            data.table_1.17.8    
 [70] hms_1.1.4             pillar_1.11.1         posterior_1.6.1      
 [73] mitools_2.4           splines_4.5.2         lattice_0.22-7       
 [76] survival_3.8-3        tidyselect_1.2.1      mix_1.0-13           
 [79] knitr_1.50            reformulas_0.4.2      gridExtra_2.3        
 [82] V8_8.0.1              urca_1.3-4            stats4_4.5.2         
 [85] xfun_0.54             bridgesampling_1.2-1  timeDate_4051.111    
 [88] matrixStats_1.5.0     stringi_1.8.7         lazyeval_0.2.2       
 [91] yaml_2.3.10           boot_1.3-32           evaluate_1.0.5       
 [94] codetools_0.2-20      cli_3.6.5             RcppParallel_5.1.11-1
 [97] rpart_4.1.24          xtable_1.8-4          Rdpack_2.6.4         
[100] processx_3.8.6        lavaan_0.6-20         coda_0.19-4.1        
[103] parallel_4.5.2        rstantools_2.5.0      fracdiff_1.5-3       
[106] bayesplot_1.14.0      Brobdingnag_1.2-9     lme4_1.1-37          
[109] viridisLite_0.4.2     mvtnorm_1.3-3         scales_1.4.0         
[112] rlang_1.1.6           multcomp_1.4-29       mnormt_2.1.1

Feedback

Please consider providing feedback about this textbook, so that I can make it as helpful as possible. You can provide feedback at the following link: https://forms.gle/LsnVKwqmS1VuxWD18

Email Notification

The online version of this book will remain open access. If you want to know when the print version of the book is for sale, enter your email below so I can let you know.