I want your feedback to make the book better for you and other readers. If you find typos, errors, or places where the text may be improved, please let me know. The best ways to provide feedback are by GitHub or hypothes.is annotations.
You can leave a comment at the bottom of the page/chapter, or open an issue or submit a pull request on GitHub: https://github.com/isaactpetersen/Fantasy-Football-Analytics-Textbook
Alternatively, you can leave an annotation using hypothes.is.
To add an annotation, select some text and then click the
symbol on the pop-up menu.
To see the annotations of others, click the
symbol in the upper right-hand corner of the page.
21 Cluster Analysis
This chapter provides an overview of cluster analysis.
21.1 Getting Started
21.1.1 Load Packages
21.1.2 Load Data
We created the player_stats_weekly.RData and player_stats_seasonal.RData objects in Section 4.4.3.
21.1.3 Overview
Whereas factor analysis evaluates how variables do or do not hang together—in terms of their associations and non-associations, cluster analysis evaluates how people are or or not similar—in terms of their scores on one or more variables. The goal of cluster analysis is to identify distinguishable subgroups of people. The people within a subgroup are expected to be more similar to each other than they are to people in other subgroups. For instance, we might expect that there are distinguishable subtypes of Wide Receivers: possession, deep threats, and slot-type Wide Receivers. Possession Wide Receivers tend to be taller and heavier, with good hands who catch the ball at a high rate. Deep threat Wide Receivers tend to be fast. Slot-type Wide Receivers tend to be small, quick, and agile. In order to identify these clusters of Wide Receivers, we might conduct a cluster analysis with variables relating to the players’ height, weight, percent of (catchable) targets caught, air yards received, and various metrics from the National Football League (NFL) Combine, including their times in the 40-yard dash, 20-yard shuttle run, and three cone drill.
There are many approaches to cluster analysis, including model-based clustering, density-based clustering, centroid-based clustering (e.g., k-means clustering), hierarchical clustering (aka connectivity-based clustering), etc. In general, cluster analysis intends to maximize intracluster similarities and to minimize intercluster similarities (Ramasubramanian & Singh, 2016). Cluster analysis is a form of an unsupervised approach to machine learning in which the groups are not known a priori. There is a risk of reifying clusters identified in cluster analysis when, in some cases, the clusters may reflect artifacts of the analytic method rather than true distinct groups (Everitt et al., 2011). In general, the classification should be judged on the extent to which it is useful rather than on the extent to which it is true or false (Everitt et al., 2011).
An overview of approaches to cluster analysis in R is provided by Kassambara (2017). In this chapter, we focus on examples using model-based clustering with the R package mclust (Fraley et al., 2024; Scrucca et al., 2023), which uses Gaussian finite mixture modeling. Model-based clustering assumes the data are generated by an underlying statistical model, and the goal is to recover the structure of that model. Model-based clustering represents the data as coming from a mixture of probability distributions. We also use k-means clustering.
There are several model fit criteria we can use to identify the optimal number of clusters in terms of the tradeoff between fit and parsimony. For the Bayesian Information Criterion (BIC), closer to zero is better. For the Integrated Complete-data Likelihood (ICL), higher is better. For the bootstrapped likelihood ratio tests, a significant likelihood ratio test indicates that the model with more clusters fits significantly better than the model with fewer clusters. Although the model fit criteria can be helpful for identifying the optimal number of clusters, they should only be used as a guide. Ultimately, cluster analysis is only useful to the extent that the clusters and useful and interpretable, which may mean selecting more (or fewer) clusters than are suggested by the model fit criteria.
For univariate cluster analyses in the mclust package (Fraley et al., 2024; Scrucca et al., 2023), there are two types of models: ones with equal variance across clusters (modelName = "E") and ones with different variances across clusters (modelName = "V"). Allowing different variances across clusters is a more complex model than forcing the clusters to have equal variances.
For multivariate cluster analyses in the mclust package (Fraley et al., 2024; Scrucca et al., 2023), models are specified by a combination of volume, shape, and orientation. The model name is specified such that the first letter corresponds to the volume, the second letter corresponds to shape, and the third letter corresponds to orientation. In terms of volume, models can be of equal volume (E) or variable volume (V) across clusters. In terms of shape, models can be of equal (E), variable (V), or identity (I) shape. In terms of orientation, models can be of equal (E), variable (V), or identity (I) orientation. The varying types of volume, shape, and orientation combine to produce three general types of covariance structures: spherical (low complexity), diagonal (moderate complexity), and ellipsoidal (high complexity). Models that allow greater differences across clusters (i.e., more V’s) are more flexible and typically more complex.
The various types of mclust models are provided here: https://mclust-org.github.io/mclust/reference/mclustModelNames.html.
21.1.4 Tiers of Prior Season Fantasy Points
21.1.4.1 Prepare Data
Code
[1] 2024Code
player_stats_seasonal_offense_recent <- player_stats_seasonal %>%
filter(season == recentSeason) %>%
filter(position_group %in% c("QB","RB","WR","TE"))
player_stats_seasonal_offense_recentQB <- player_stats_seasonal_offense_recent %>%
filter(position_group == "QB")
player_stats_seasonal_offense_recentRB <- player_stats_seasonal_offense_recent %>%
filter(position_group == "RB")
player_stats_seasonal_offense_recentWR <- player_stats_seasonal_offense_recent %>%
filter(position_group == "WR")
player_stats_seasonal_offense_recentTE <- player_stats_seasonal_offense_recent %>%
filter(position_group == "TE")21.1.4.2 Identify the Optimal Number of Tiers by Position
We can evaluate how many clusters to keep, based on the tradeoff between fit and parsimony, using the mclust::mclustBIC() (BIC), mclust::mclustICL() (ICL), and mclust::mclustBootstrapLRT() (bootstrapped likelihood ratio tests) functions of the mclust package (Fraley et al., 2024; Scrucca et al., 2023). We can also use k-means clustering using the stats::kmeans() function.
21.1.4.2.1 Quarterbacks
21.1.4.2.1.1 Model-Based Clustering
Code
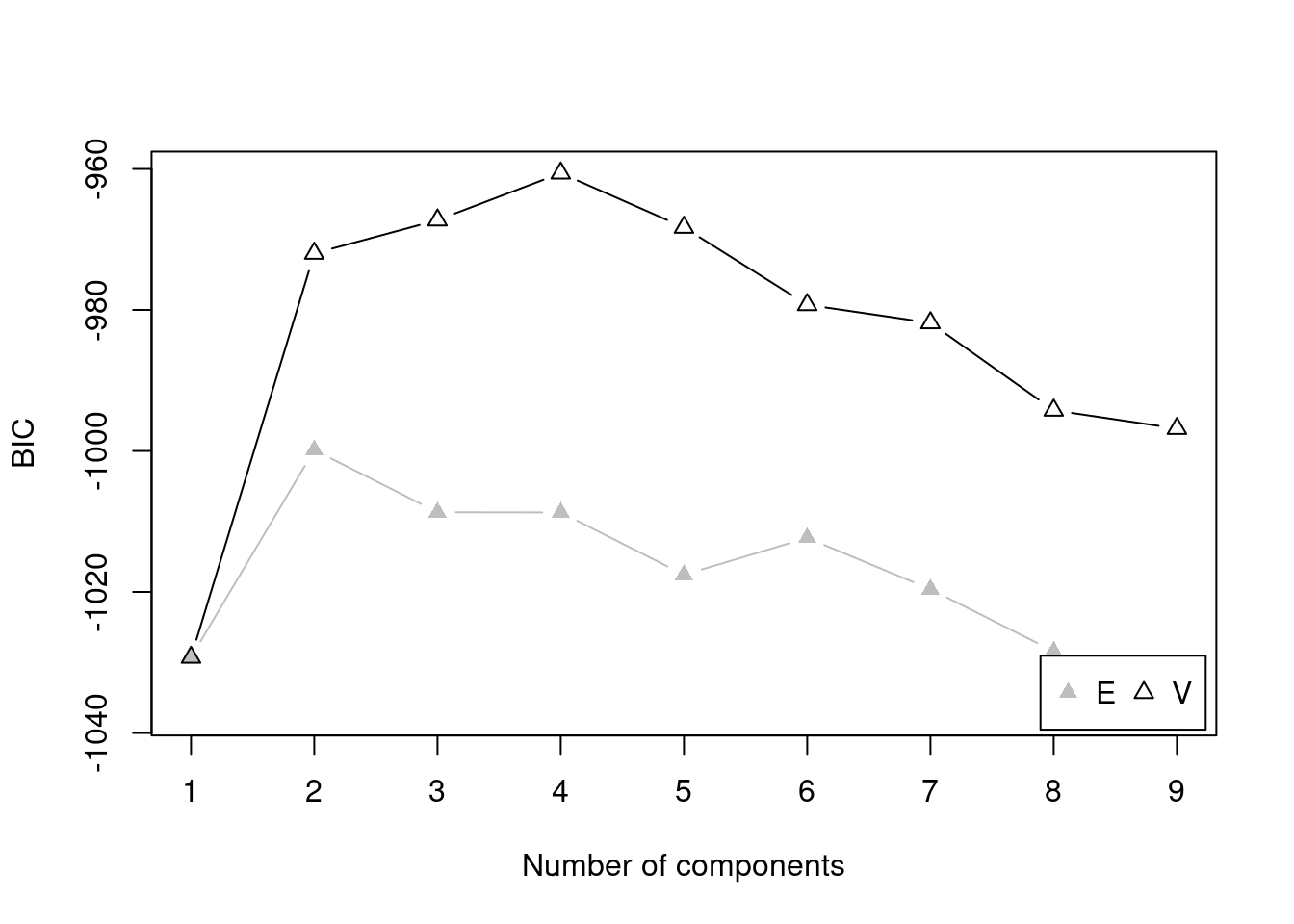
Bayesian Information Criterion (BIC):
E V
1 -982.9038 -982.9038
2 -964.3518 -927.2534
3 -973.0978 -930.5327
4 -971.2212 -912.2067
5 -971.1002 -924.2192
6 -979.8174 -928.6330
7 -974.9956 -949.0362
8 -981.8676 -955.9257
9 -990.5409 -963.9506
Top 3 models based on the BIC criterion:
V,4 V,5 V,2
-912.2067 -924.2192 -927.2534 Best BIC values:
V,4 V,5 V,2
BIC -912.2067 -924.21918 -927.25337
BIC diff 0.0000 -12.01245 -15.04664
Code
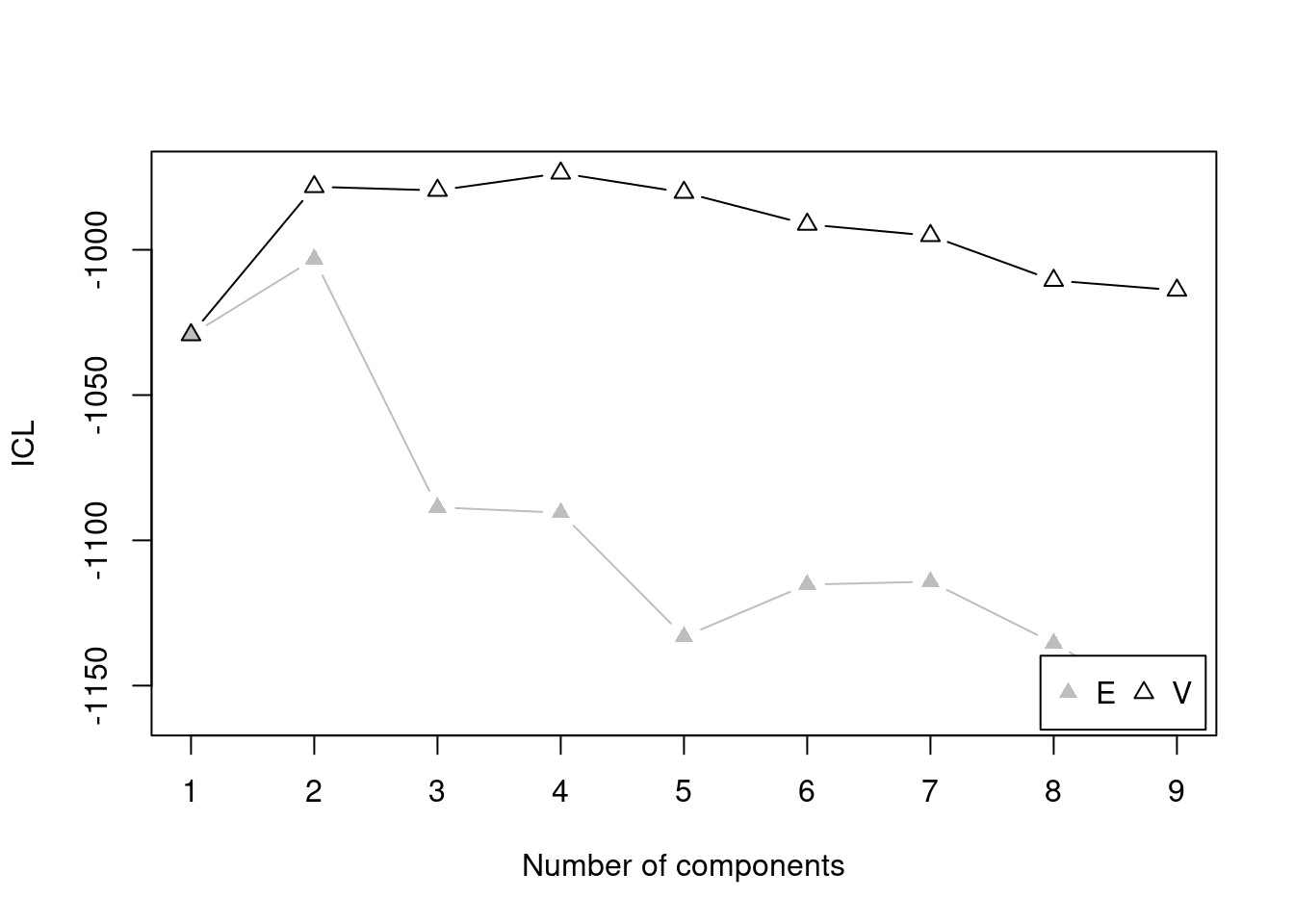
Integrated Complete-data Likelihood (ICL) criterion:
E V
1 -982.9038 -982.9038
2 -972.1069 -933.7840
3 -1039.9236 -945.9954
4 -1040.3715 -927.2426
5 -1033.2208 -945.8315
6 -1061.5988 -935.2325
7 -1056.6193 -993.1199
8 -1065.2675 -976.8222
9 -1088.2374 -986.9286
Top 3 models based on the ICL criterion:
V,4 V,2 V,6
-927.2426 -933.7840 -935.2325 Best ICL values:
V,4 V,2 V,6
ICL -927.2426 -933.78400 -935.232482
ICL diff 0.0000 -6.54137 -7.989849
Code
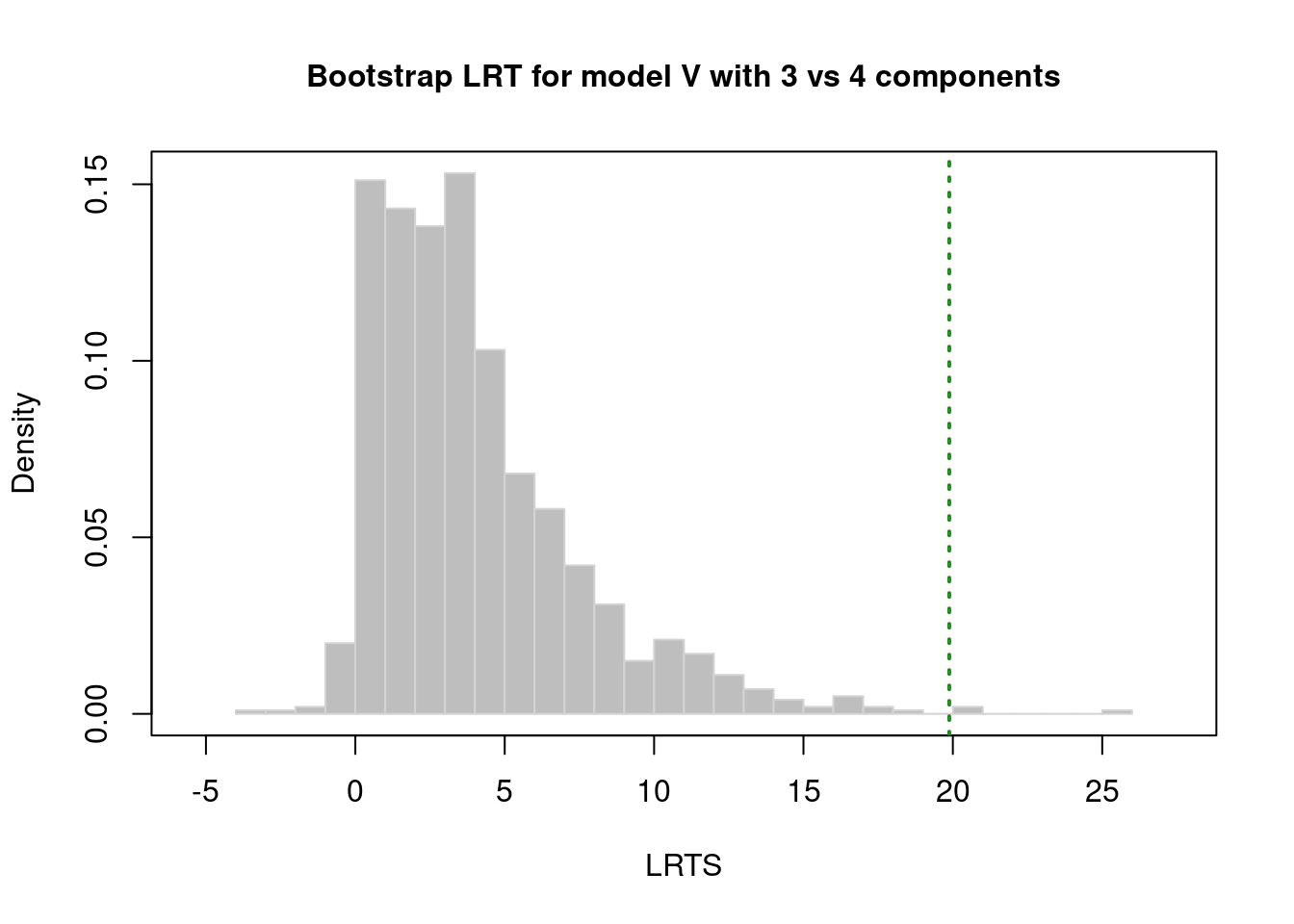
tiersQB_bootstrap <- mclust::mclustBootstrapLRT(
data = player_stats_seasonal_offense_recentQB$fantasyPoints,
modelName = "V") # variable/unequal variance (for univariate data)
numTiersQB <- as.numeric(summary(tiersQB_bootstrap)[,"Length"][1]) # or could specify the number of teams manually
tiersQB_bootstrap-------------------------------------------------------------
Bootstrap sequential LRT for the number of mixture components
-------------------------------------------------------------
Model = V
Replications = 999
LRTS bootstrap p-value
1 vs 2 68.720575 0.001
2 vs 3 9.790787 0.046
3 vs 4 31.396105 0.001
4 vs 5 1.057678 0.682
21.1.4.2.1.2 k-Means Clustering
Code
K-means clustering with 4 clusters of sizes 10, 16, 17, 35
Cluster means:
[,1]
1 199.19200
2 328.35875
3 108.57529
4 14.95657
Clustering vector:
[1] 2 3 3 1 4 2 2 4 2 1 1 2 4 4 4 3 3 3 4 1 3 4 4 1 3 3 2 4 4 4 4 2 3 2 4 2 4 2
[39] 3 4 1 2 4 4 3 2 4 1 4 4 2 2 3 4 4 3 1 4 4 4 4 2 1 2 4 4 3 4 4 4 4 3 4 1 3 4
[77] 4 3
Within cluster sum of squares by cluster:
[1] 5696.539 41943.075 11520.715 8744.099
(between_SS / total_SS = 94.4 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 21.1.4.2.2 Running Backs
21.1.4.2.2.1 Model-Based Clustering
Code
Bayesian Information Criterion (BIC):
E V
1 -1854.031 -1854.031
2 -1786.170 -1741.345
3 -1796.289 -1681.204
4 -1786.692 -1683.266
5 -1796.779 -1688.302
6 -1806.869 -1699.238
7 -1788.245 -1713.803
8 -1798.339 -1714.711
9 -1805.916 -1729.569
Top 3 models based on the BIC criterion:
V,3 V,4 V,5
-1681.204 -1683.266 -1688.302 Best BIC values:
V,3 V,4 V,5
BIC -1681.204 -1683.266361 -1688.302292
BIC diff 0.000 -2.062052 -7.097982
Code
Integrated Complete-data Likelihood (ICL) criterion:
E V
1 -1854.031 -1854.031
2 -1791.597 -1765.263
3 -1955.631 -1710.036
4 -1940.803 -1727.646
5 -2032.425 -1729.461
6 -2085.572 -1739.405
7 -2049.102 -1771.322
8 -2088.752 -1774.842
9 -2104.642 -1806.327
Top 3 models based on the ICL criterion:
V,3 V,4 V,5
-1710.036 -1727.646 -1729.461 Best ICL values:
V,3 V,4 V,5
ICL -1710.036 -1727.64580 -1729.46112
ICL diff 0.000 -17.61014 -19.42546
Code
-------------------------------------------------------------
Bootstrap sequential LRT for the number of mixture components
-------------------------------------------------------------
Model = V
Replications = 999
LRTS bootstrap p-value
1 vs 2 127.81623 0.001
2 vs 3 75.27109 0.001
3 vs 4 13.06822 0.011
4 vs 5 10.09434 0.061
21.1.4.2.2.2 k-Means Clustering
Code
K-means clustering with 4 clusters of sizes 45, 25, 57, 28
Cluster means:
[,1]
1 46.022222
2 119.104000
3 6.547368
4 251.979286
Clustering vector:
[1] 4 3 3 1 2 4 2 3 2 1 2 3 4 1 3 3 2 4 2 3 4 3 2 1 4 1 3 1 1 4 3 3 1 3 4 1 1
[38] 3 3 1 3 1 3 4 4 1 4 3 2 3 2 1 3 1 3 3 1 1 1 2 1 1 3 4 1 3 4 3 2 1 4 4 3 2
[75] 2 1 3 1 3 2 4 3 4 3 3 2 1 4 3 3 2 2 3 3 3 3 1 3 1 4 3 1 3 1 1 4 3 1 1 3 1
[112] 3 4 1 3 1 1 4 3 1 3 2 3 4 4 3 1 2 4 1 1 3 2 3 3 4 2 3 3 1 1 3 1 2 2 2 3 1
[149] 3 4 3 3 4 2 1
Within cluster sum of squares by cluster:
[1] 11197.738 13089.590 2733.462 78847.676
(between_SS / total_SS = 92.1 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 21.1.4.2.3 Wide Receivers
21.1.4.2.3.1 Model-Based Clustering
Code
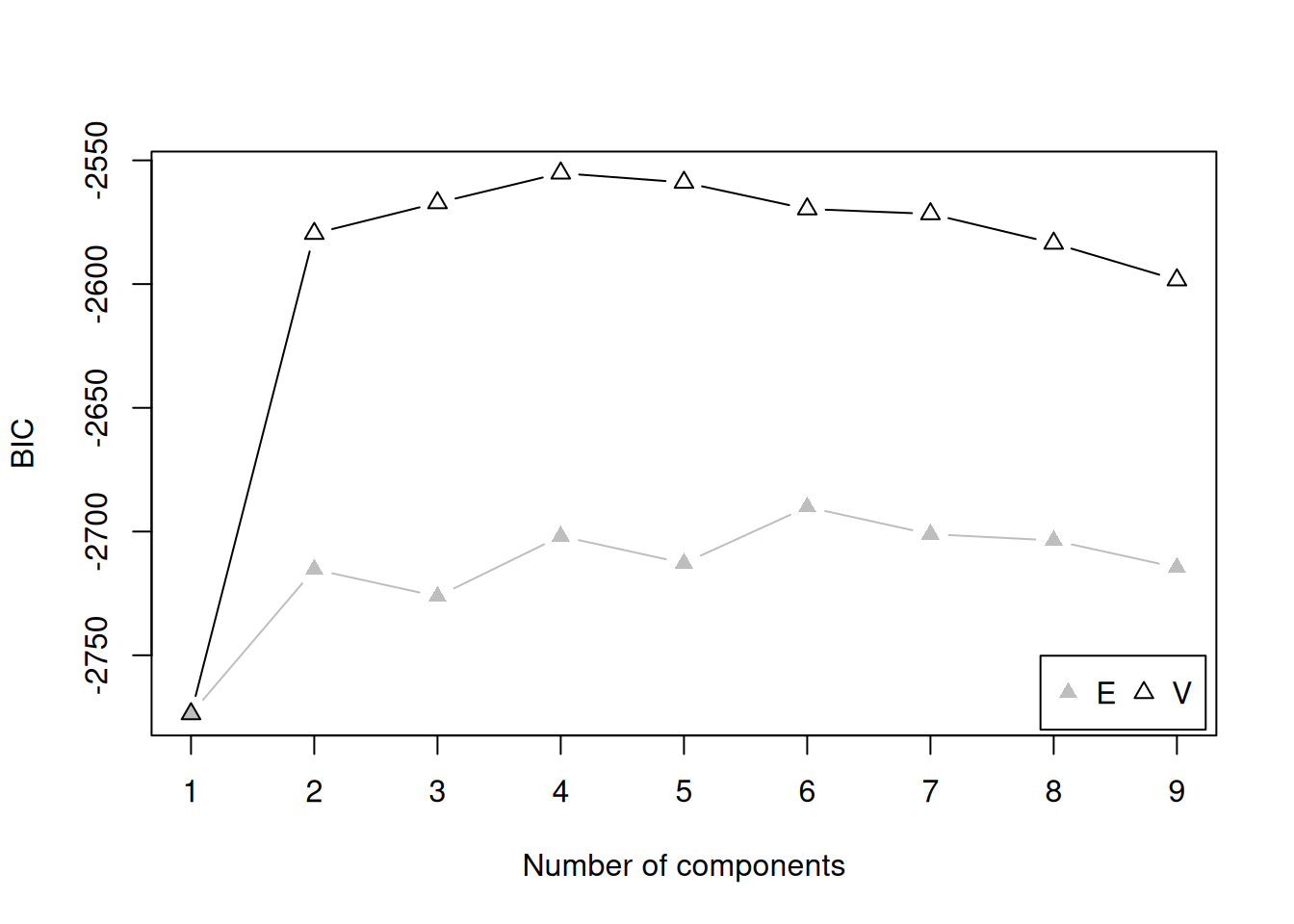
Bayesian Information Criterion (BIC):
E V
1 -2773.668 -2773.668
2 -2715.276 -2579.573
3 -2726.221 -2567.175
4 -2701.874 -2555.180
5 -2712.788 -2558.928
6 -2690.115 -2569.660
7 -2701.052 -2571.626
8 -2703.583 -2583.527
9 -2714.560 -2598.340
Top 3 models based on the BIC criterion:
V,4 V,5 V,3
-2555.180 -2558.928 -2567.175 Best BIC values:
V,4 V,5 V,3
BIC -2555.18 -2558.928068 -2567.17473
BIC diff 0.00 -3.748463 -11.99512
Code
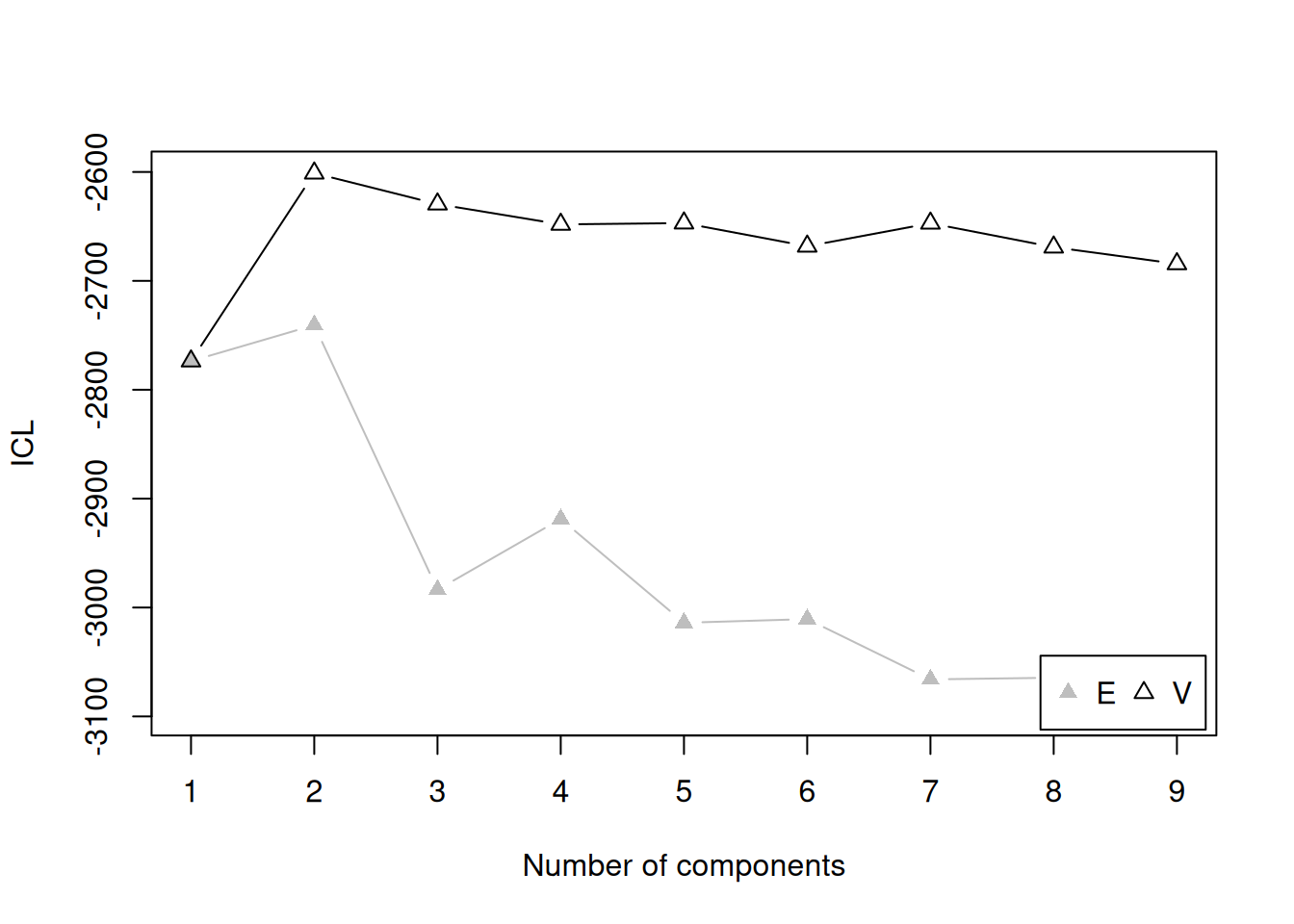
Integrated Complete-data Likelihood (ICL) criterion:
E V
1 -2773.668 -2773.668
2 -2740.609 -2601.071
3 -2983.660 -2629.491
4 -2918.630 -2648.113
5 -3013.988 -2646.928
6 -3010.614 -2668.189
7 -3065.987 -2647.081
8 -3064.463 -2669.032
9 -3097.662 -2684.364
Top 3 models based on the ICL criterion:
V,2 V,3 V,5
-2601.071 -2629.491 -2646.928 Best ICL values:
V,2 V,3 V,5
ICL -2601.071 -2629.49065 -2646.92847
ICL diff 0.000 -28.41921 -45.85703
Code
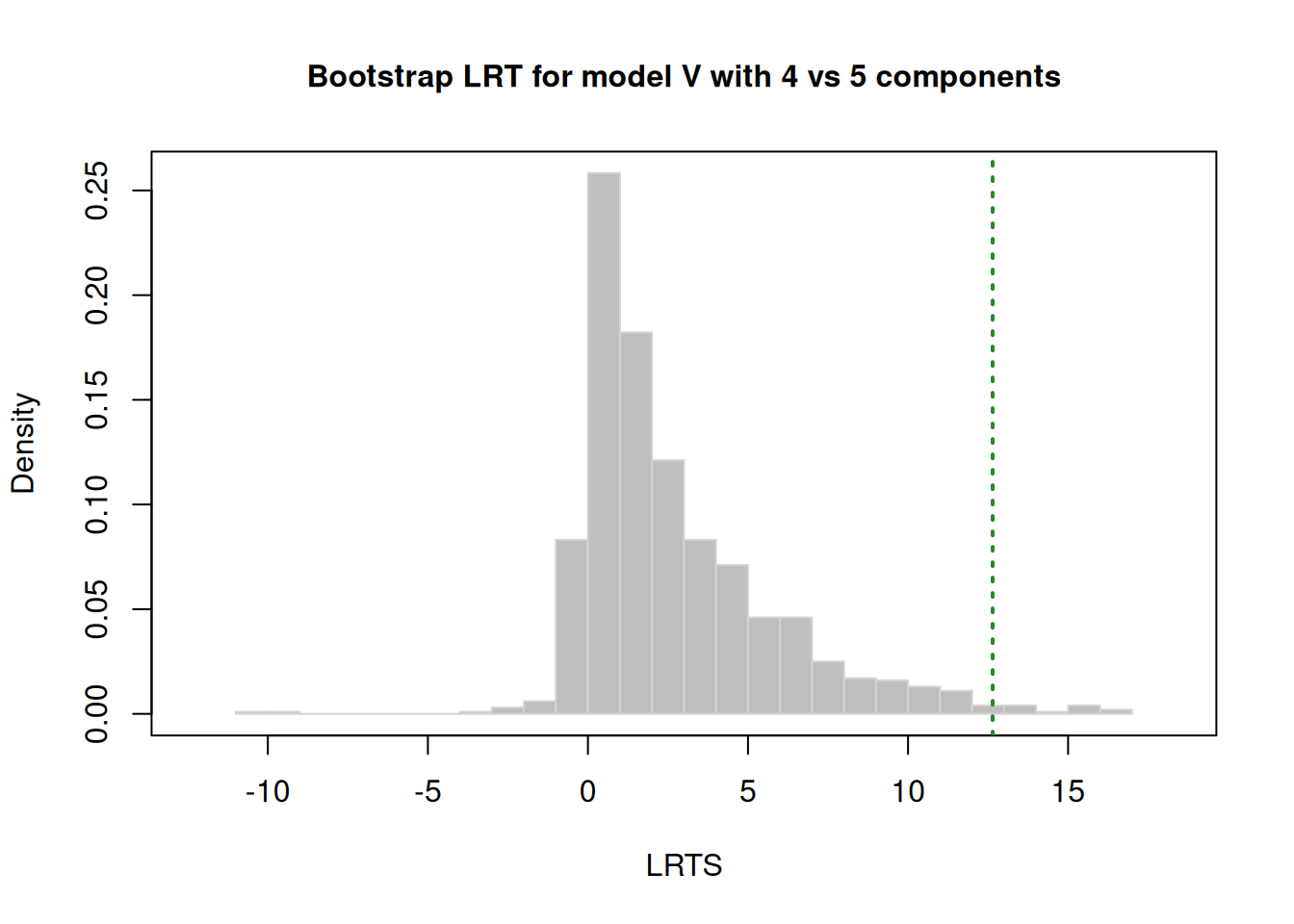
tiersWR_bootstrap <- mclust::mclustBootstrapLRT(
data = player_stats_seasonal_offense_recentWR$fantasyPoints,
modelName = "V") # variable/unequal variance (for univariate data)
numTiersWR <- as.numeric(summary(tiersWR_bootstrap)[,"Length"][1]) # or could specify the number of teams manually
tiersWR_bootstrap-------------------------------------------------------------
Bootstrap sequential LRT for the number of mixture components
-------------------------------------------------------------
Model = V
Replications = 999
LRTS bootstrap p-value
1 vs 2 210.486649 0.001
2 vs 3 28.790091 0.001
3 vs 4 28.386617 0.001
4 vs 5 12.643032 0.014
5 vs 6 5.659307 0.166
21.1.4.2.3.2 k-Means Clustering
Code
K-means clustering with 5 clusters of sizes 112, 43, 27, 38, 16
Cluster means:
[,1]
1 10.95804
2 66.12000
3 196.88148
4 126.74526
5 275.69125
Clustering vector:
[1] 3 4 2 1 3 1 1 4 1 4 5 4 1 1 1 1 1 1 2 2 1 1 1 5 1 1 1 1 1 4 3 1 2 2 5 1 1
[38] 1 4 2 2 4 1 1 1 3 5 2 1 5 2 3 1 1 1 4 3 5 1 2 1 4 4 3 1 4 4 1 2 4 1 1 1 2
[75] 4 5 2 4 1 2 5 3 1 2 1 1 1 1 1 5 1 1 2 1 3 2 2 4 4 1 4 1 1 1 1 3 1 3 1 5 3
[112] 4 1 1 5 1 2 1 1 1 3 2 3 4 2 2 5 1 2 1 1 4 1 1 2 1 4 3 1 2 4 1 1 3 1 5 1 2
[149] 1 4 1 1 5 2 2 1 3 4 1 1 1 1 3 4 5 2 1 1 2 4 3 1 2 1 4 4 1 3 3 1 1 2 2 3 4
[186] 2 1 1 2 4 4 1 1 2 1 1 1 4 2 1 4 1 3 1 5 1 2 1 4 1 1 1 1 1 2 4 2 2 2 4 1 1
[223] 3 1 1 2 3 1 1 4 1 1 3 1 3 1
Within cluster sum of squares by cluster:
[1] 11828.313 11808.246 8363.421 9771.061 28698.398
(between_SS / total_SS = 95.8 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 21.1.4.2.4 Tight Ends
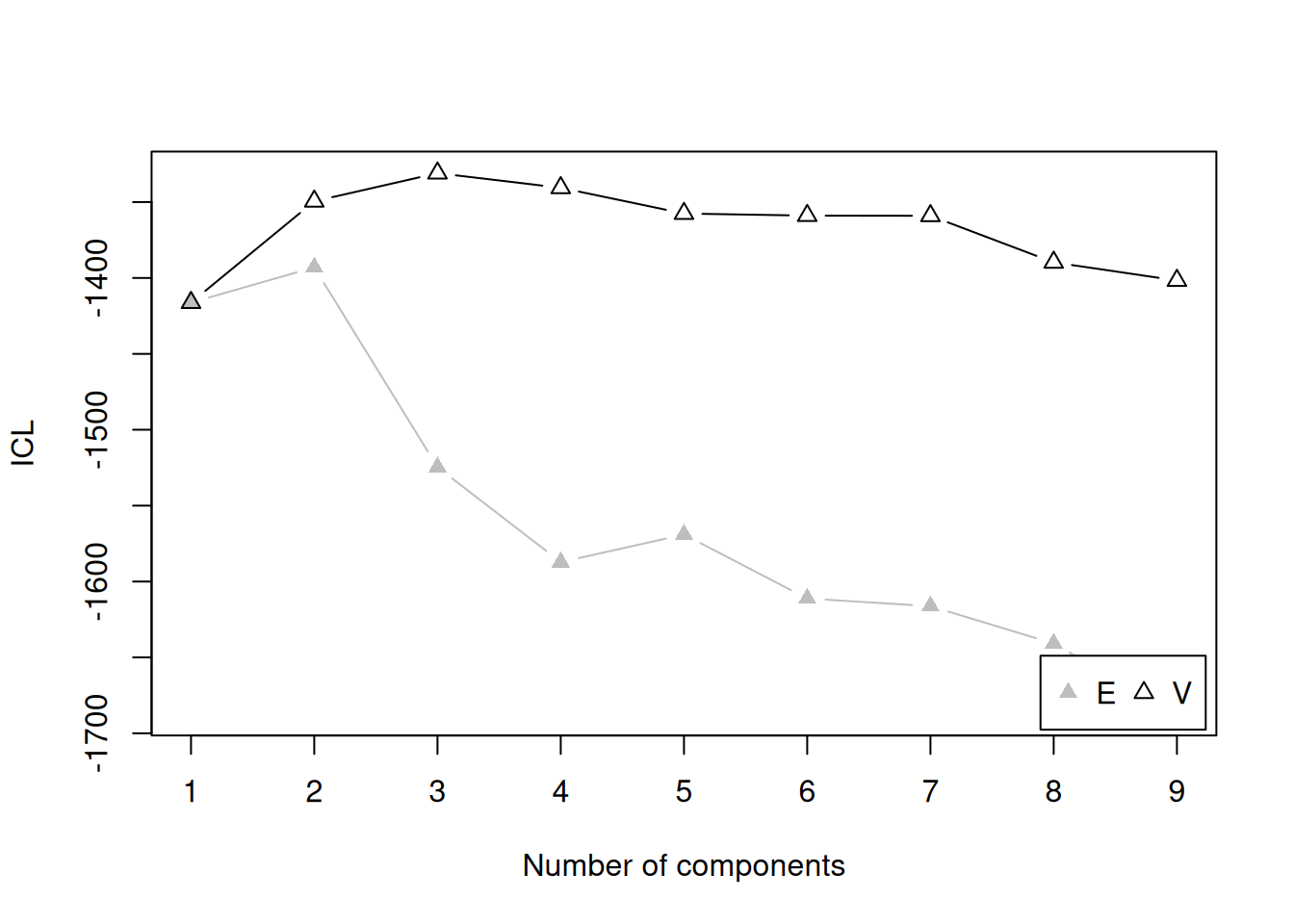
21.1.4.2.4.1 Model-Based Clustering
Code
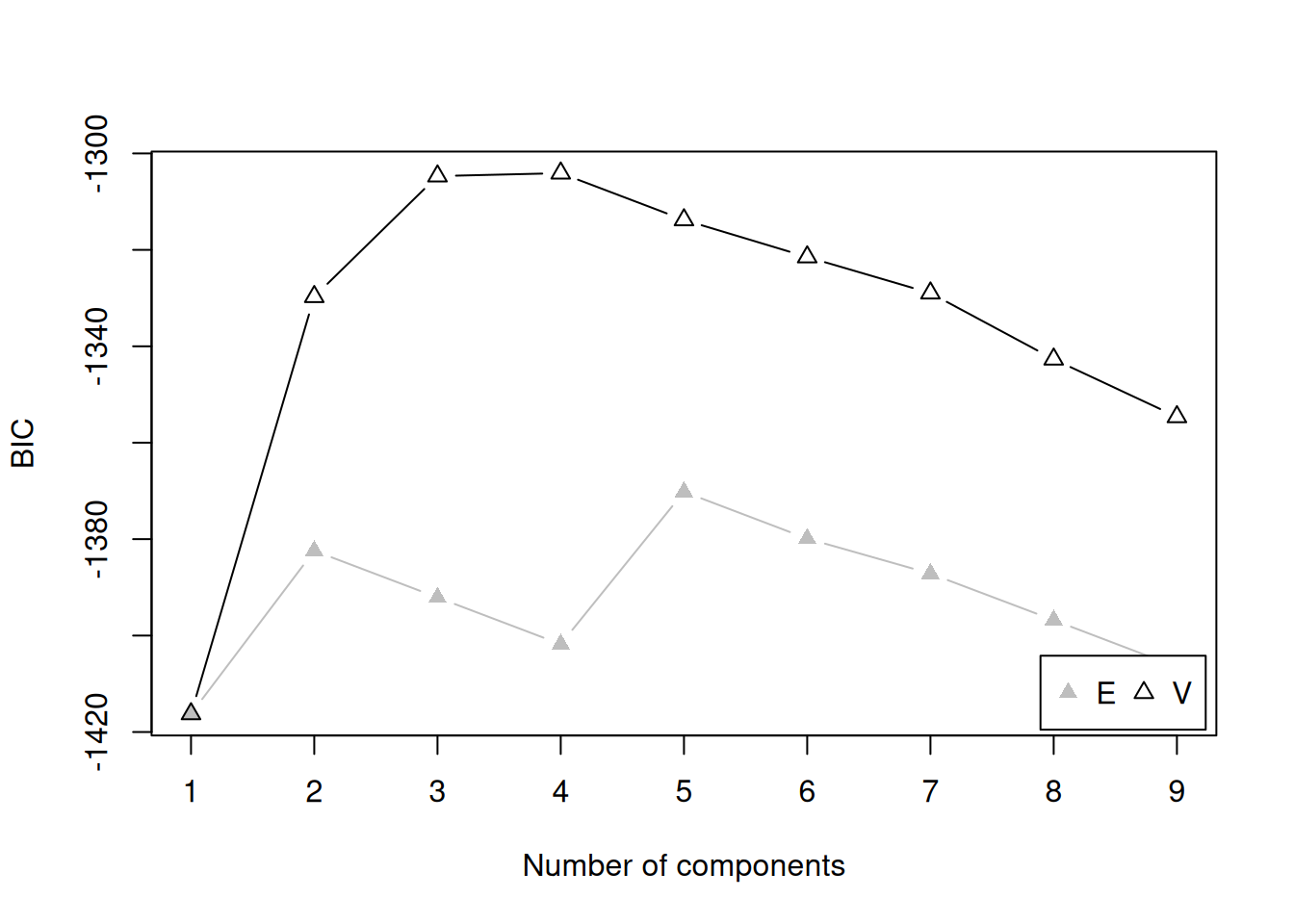
Bayesian Information Criterion (BIC):
E V
1 -1416.237 -1416.237
2 -1382.407 -1329.715
3 -1392.097 -1304.704
4 -1401.790 -1304.096
5 -1370.177 -1313.794
6 -1379.889 -1321.488
7 -1387.142 -1328.972
8 -1396.793 -1342.684
9 -1406.526 -1354.634
Top 3 models based on the BIC criterion:
V,4 V,3 V,5
-1304.096 -1304.704 -1313.794 Best BIC values:
V,4 V,3 V,5
BIC -1304.096 -1304.7036430 -1313.794382
BIC diff 0.000 -0.6074285 -9.698167
Code
Integrated Complete-data Likelihood (ICL) criterion:
E V
1 -1416.237 -1416.237
2 -1392.973 -1349.457
3 -1524.660 -1330.942
4 -1587.201 -1340.591
5 -1569.061 -1357.545
6 -1611.215 -1358.914
7 -1616.252 -1359.035
8 -1640.868 -1389.717
9 -1687.213 -1401.670
Top 3 models based on the ICL criterion:
V,3 V,4 V,2
-1330.942 -1340.591 -1349.457 Best ICL values:
V,3 V,4 V,2
ICL -1330.942 -1340.590921 -1349.45661
ICL diff 0.000 -9.648454 -18.51414
Code
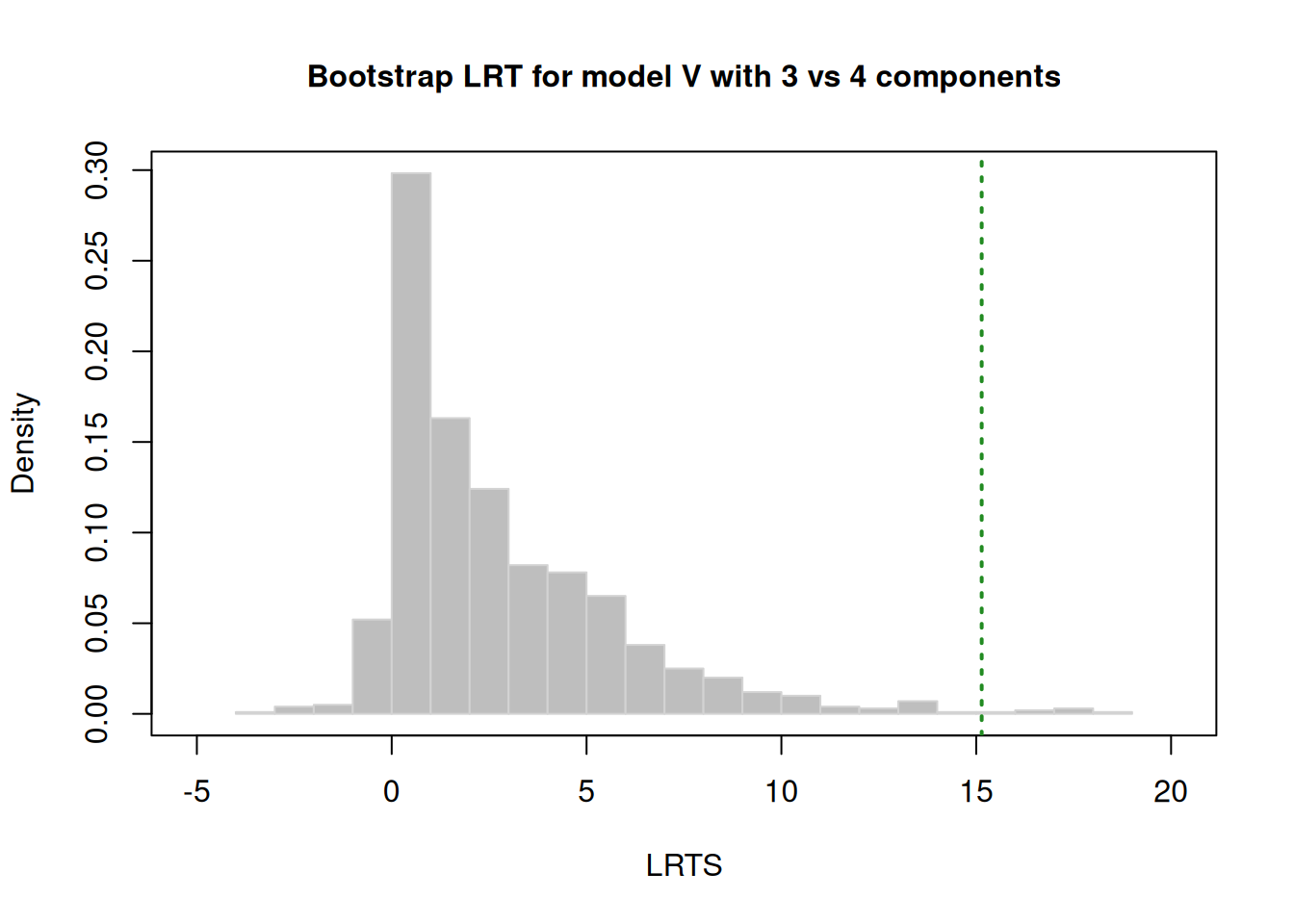
tiersTE_bootstrap <- mclust::mclustBootstrapLRT(
data = player_stats_seasonal_offense_recentTE$fantasyPoints,
modelName = "V") # variable/unequal variance (for univariate data)
numTiersTE <- as.numeric(summary(tiersTE_bootstrap)[,"Length"][1]) # or could specify the number of teams manually
tiersTE_bootstrap-------------------------------------------------------------
Bootstrap sequential LRT for the number of mixture components
-------------------------------------------------------------
Model = V
Replications = 999
LRTS bootstrap p-value
1 vs 2 101.054621 0.001
2 vs 3 39.543494 0.001
3 vs 4 15.139990 0.008
4 vs 5 4.834394 0.227
21.1.4.2.4.2 k-Means Clustering
Code
K-means clustering with 4 clusters of sizes 61, 10, 25, 31
Cluster means:
[,1]
1 9.062295
2 206.120000
3 115.313600
4 46.077419
Clustering vector:
[1] 3 4 4 1 3 1 1 1 1 1 1 3 1 1 2 4 1 3 4 1 4 1 3 1 4 3 1 1 3 1 3 3 4 4 1 3 1
[38] 4 1 4 1 1 4 4 1 4 3 1 3 1 2 1 4 1 1 1 3 1 1 3 4 1 1 3 1 1 4 1 1 1 4 2 3 1
[75] 1 4 4 1 1 3 1 1 3 4 4 1 1 4 1 2 4 3 4 1 4 4 3 3 2 4 1 1 1 1 1 1 2 1 1 4 3
[112] 1 4 3 4 1 4 2 2 1 2 3 1 3 1 1 2
Within cluster sum of squares by cluster:
[1] 3441.063 11340.036 9032.027 5681.434
(between_SS / total_SS = 93.9 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 21.1.4.3 Fit the Cluster Model to the Optimal Number of Tiers
21.1.4.3.1 Quarterbacks
In our data, all of the following models are equivalent—i.e., they result in the same unequal variance model with a 4-cluster solution—but they arrive there in different ways. We can fit the cluster model to the optimal number of tiers using the mclust::Mclust() function.
Code
mclust::Mclust(
data = player_stats_seasonal_offense_recentQB$fantasyPoints,
G = numTiersQB,
)
mclust::Mclust(
data = player_stats_seasonal_offense_recentQB$fantasyPoints,
G = 4,
)
mclust::Mclust(
data = player_stats_seasonal_offense_recentQB$fantasyPoints,
)
mclust::Mclust(
data = player_stats_seasonal_offense_recentQB$fantasyPoints,
x = tiersQB_bic
)Let’s fit one of these:
Here are the number of players that are in each of the four clusters (i.e., tiers):
21.1.4.3.2 Running Backs
Here are the number of players that are in each of the four clusters (i.e., tiers):
21.1.4.3.3 Wide Receivers
Here are the number of players that are in each of the four clusters (i.e., tiers):
21.1.4.3.4 Tight Ends
Here are the number of players that are in each of the four clusters (i.e., tiers):
21.1.4.4 Plot the Tiers
We can merge the player’s classification into the dataset and plot each player’s classification.
21.1.4.4.1 Quarterbacks
Code
player_stats_seasonal_offense_recentQB$tier <- clusterModelQBs$classification
player_stats_seasonal_offense_recentQB <- player_stats_seasonal_offense_recentQB %>%
mutate(
tier = factor(max(tier, na.rm = TRUE) + 1 - tier)
)
player_stats_seasonal_offense_recentQB$position_rank <- rank(
player_stats_seasonal_offense_recentQB$fantasyPoints * -1,
na.last = "keep",
ties.method = "min")
plot_qbTiers <- ggplot2::ggplot(
data = player_stats_seasonal_offense_recentQB,
mapping = aes(
x = fantasyPoints,
y = position_rank,
color = tier
)) +
geom_point(
aes(
text = player_display_name # add player name for mouse over tooltip
)) +
scale_y_continuous(trans = "reverse") +
coord_cartesian(clip = "off") +
labs(
x = "Projected Points",
y = "Position Rank",
title = "Quarterback Fantasy Points by Tier",
color = "Tier") +
theme_classic() +
theme(legend.position = "top")
plotly::ggplotly(plot_qbTiers)21.1.4.4.2 Running Backs
Code
player_stats_seasonal_offense_recentRB$tier <- clusterModelRBs$classification
player_stats_seasonal_offense_recentRB <- player_stats_seasonal_offense_recentRB %>%
mutate(
tier = factor(max(tier, na.rm = TRUE) + 1 - tier)
)
player_stats_seasonal_offense_recentRB$position_rank <- rank(
player_stats_seasonal_offense_recentRB$fantasyPoints * -1,
na.last = "keep",
ties.method = "min")
plot_rbTiers <- ggplot2::ggplot(
data = player_stats_seasonal_offense_recentRB,
mapping = aes(
x = fantasyPoints,
y = position_rank,
color = tier
)) +
geom_point(
aes(
text = player_display_name # add player name for mouse over tooltip
)) +
scale_y_continuous(trans = "reverse") +
coord_cartesian(clip = "off") +
labs(
x = "Projected Points",
y = "Position Rank",
title = "Running Back Fantasy Points by Tier",
color = "Tier") +
theme_classic() +
theme(legend.position = "top")
plotly::ggplotly(plot_rbTiers)21.1.4.4.3 Wide Receivers
Code
player_stats_seasonal_offense_recentWR$tier <- clusterModelWRs$classification
player_stats_seasonal_offense_recentWR <- player_stats_seasonal_offense_recentWR %>%
mutate(
tier = factor(max(tier, na.rm = TRUE) + 1 - tier)
)
player_stats_seasonal_offense_recentWR$position_rank <- rank(
player_stats_seasonal_offense_recentWR$fantasyPoints * -1,
na.last = "keep",
ties.method = "min")
plot_wrTiers <- ggplot2::ggplot(
data = player_stats_seasonal_offense_recentWR,
mapping = aes(
x = fantasyPoints,
y = position_rank,
color = tier
)) +
geom_point(
aes(
text = player_display_name # add player name for mouse over tooltip
)) +
scale_y_continuous(trans = "reverse") +
coord_cartesian(clip = "off") +
labs(
x = "Projected Points",
y = "Position Rank",
title = "Wide Receiver Fantasy Points by Tier",
color = "Tier") +
theme_classic() +
theme(legend.position = "top")
plotly::ggplotly(plot_wrTiers)21.1.4.4.4 Tight Ends
Code
player_stats_seasonal_offense_recentTE$tier <- clusterModelTEs$classification
player_stats_seasonal_offense_recentTE <- player_stats_seasonal_offense_recentTE %>%
mutate(
tier = factor(max(tier, na.rm = TRUE) + 1 - tier)
)
player_stats_seasonal_offense_recentTE$position_rank <- rank(
player_stats_seasonal_offense_recentTE$fantasyPoints * -1,
na.last = "keep",
ties.method = "min")
plot_teTiers <- ggplot2::ggplot(
data = player_stats_seasonal_offense_recentTE,
mapping = aes(
x = fantasyPoints,
y = position_rank,
color = tier
)) +
geom_point(
aes(
text = player_display_name # add player name for mouse over tooltip
)) +
scale_y_continuous(trans = "reverse") +
coord_cartesian(clip = "off") +
labs(
x = "Projected Points",
y = "Position Rank",
title = "Tight End Fantasy Points by Tier",
color = "Tier") +
theme_classic() +
theme(legend.position = "top")
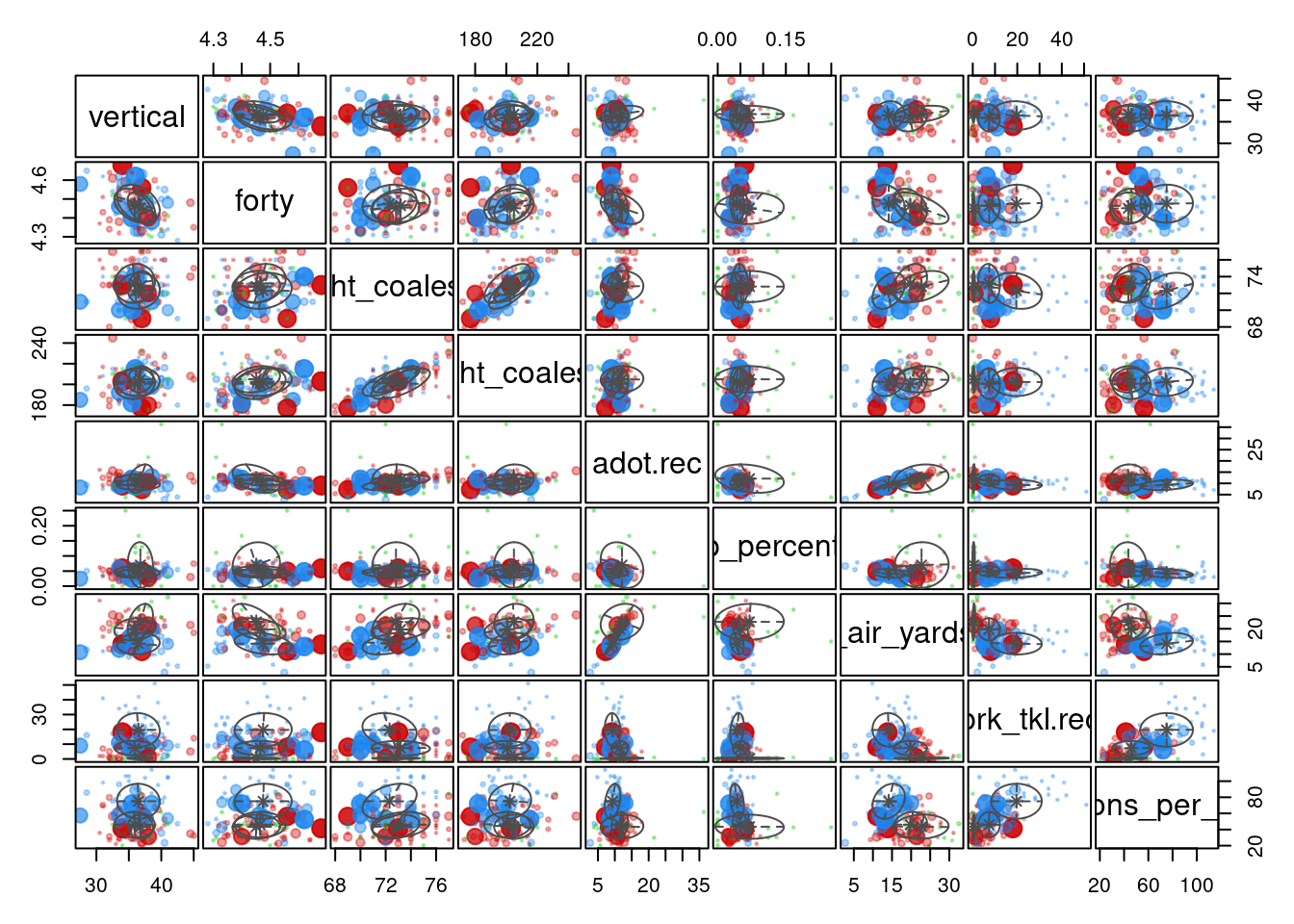
plotly::ggplotly(plot_teTiers)21.1.5 Types of Wide Receivers
Code
# Compute Advanced PFR Stats by Career
pfrVars <- nfl_advancedStatsPFR_seasonal %>%
select(pocket_time.pass:cmp_percent.def, g, gs) %>%
names()
weightedAverageVars <- c(
"pocket_time.pass",
"ybc_att.rush","yac_att.rush",
"ybc_r.rec","yac_r.rec","adot.rec","rat.rec",
"yds_cmp.def","yds_tgt.def","dadot.def","m_tkl_percent.def","rat.def"
)
recomputeVars <- c(
"drop_pct.pass", # drops.pass / pass_attempts.pass
"bad_throw_pct.pass", # bad_throws.pass / pass_attempts.pass
"on_tgt_pct.pass", # on_tgt_throws.pass / pass_attempts.pass
"pressure_pct.pass", # times_pressured.pass / pass_attempts.pass
"drop_percent.rec", # drop.rec / tgt.rec
"rec_br.rec", # rec.rec / brk_tkl.rec
"cmp_percent.def" # cmp.def / tgt.def
)
sumVars <- pfrVars[pfrVars %ni% c(
weightedAverageVars, recomputeVars,
"merge_name", "loaded.pass", "loaded.rush", "loaded.rec", "loaded.def")]
nfl_advancedStatsPFR_career <- nfl_advancedStatsPFR_seasonal %>%
group_by(pfr_id, merge_name) %>%
summarise(
across(all_of(weightedAverageVars), ~ weighted.mean(.x, w = g, na.rm = TRUE)),
across(all_of(sumVars), ~ sum(.x, na.rm = TRUE)),
.groups = "drop") %>%
mutate(
drop_pct.pass = drops.pass / pass_attempts.pass,
bad_throw_pct.pass = bad_throws.pass / pass_attempts.pass,
on_tgt_pct.pass = on_tgt_throws.pass / pass_attempts.pass,
pressure_pct.pass = times_pressured.pass / pass_attempts.pass,
drop_percent.rec = drop.rec / tgt.rec,
rec_br.rec = drop.rec / tgt.rec,
cmp_percent.def = cmp.def / tgt.def
)
uniqueCases <- nfl_advancedStatsPFR_seasonal %>% select(pfr_id, merge_name, gsis_id) %>% unique()
uniqueCases %>%
group_by(pfr_id) %>%
filter(n() > 1)Code
nfl_advancedStatsPFR_seasonal <- nfl_advancedStatsPFR_seasonal %>%
filter(pfr_id != "WillMa06" | merge_name != "MARCUSWILLIAMS" | !is.na(gsis_id))
nfl_advancedStatsPFR_career <- left_join(
nfl_advancedStatsPFR_career,
nfl_advancedStatsPFR_seasonal %>% select(pfr_id, merge_name, gsis_id) %>% unique(),
by = c("pfr_id", "merge_name")
)
# Compute Player Stats Per Season
player_stats_seasonal_careerWRs <- player_stats_seasonal %>%
filter(position == "WR") %>%
group_by(player_id) %>%
summarise(
across(all_of(c("targets", "receptions", "receiving_air_yards")), ~ weighted.mean(.x, w = games, na.rm = TRUE)),
.groups = "drop")
# Drop players with no receiving air yards
player_stats_seasonal_careerWRs <- player_stats_seasonal_careerWRs %>%
filter(receiving_air_yards != 0) %>%
rename(
targets_per_season = targets,
receptions_per_season = receptions,
receiving_air_yards_per_season = receiving_air_yards
)
# Merge
playerListToMerge <- list(
nfl_players %>% select(gsis_id, display_name, position, height, weight),
nfl_combine %>% select(gsis_id, vertical, forty, ht, wt),
player_stats_seasonal_careerWRs %>% select(player_id, targets_per_season, receptions_per_season, receiving_air_yards_per_season) %>%
rename(gsis_id = player_id),
nfl_actualStats_career_player_inclPost %>% select(player_id, receptions, targets, receiving_air_yards, air_yards_share, target_share) %>%
rename(gsis_id = player_id),
nfl_advancedStatsPFR_career %>% select(gsis_id, adot.rec, rec.rec, brk_tkl.rec, drop.rec, drop_percent.rec)
)
merged_data <- playerListToMerge %>%
reduce(
full_join,
by = c("gsis_id"),
na_matches = "never")Additional processing:
Code
merged_data <- merged_data %>%
mutate(
height_coalesced = coalesce(height, ht),
weight_coalesced = coalesce(weight, wt),
receptions_coalesced = pmax(receptions, rec.rec, na.rm = TRUE),
receiving_air_yards_per_rec = receiving_air_yards / receptions
)
merged_data$receiving_air_yards_per_rec[which(merged_data$receptions == 0)] <- 0
merged_dataWRs <- merged_data %>%
filter(position == "WR")
merged_dataWRs_cluster <- merged_dataWRs %>%
filter(receptions_coalesced >= 100) %>% # keep WRs with at least 100 receptions
select(gsis_id, display_name, vertical, forty, height_coalesced, weight_coalesced, adot.rec, drop_percent.rec, receiving_air_yards_per_rec, brk_tkl.rec, receptions_per_season) %>% #targets_per_season, receiving_air_yards_per_season, air_yards_share, target_share
na.omit()21.1.5.1 Identify the Number of WR Types
21.1.5.1.1 Model-Based Clustering
Code
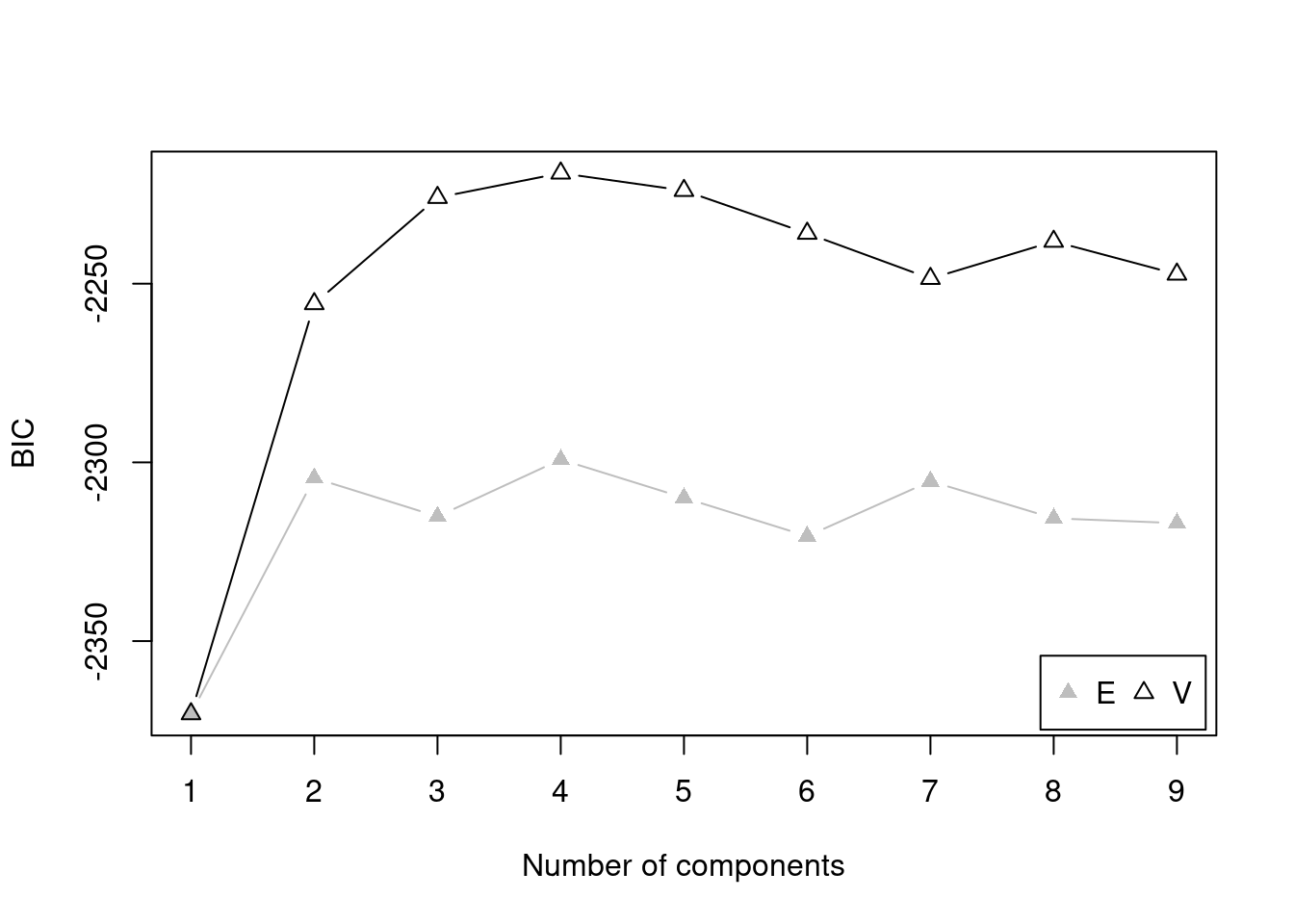
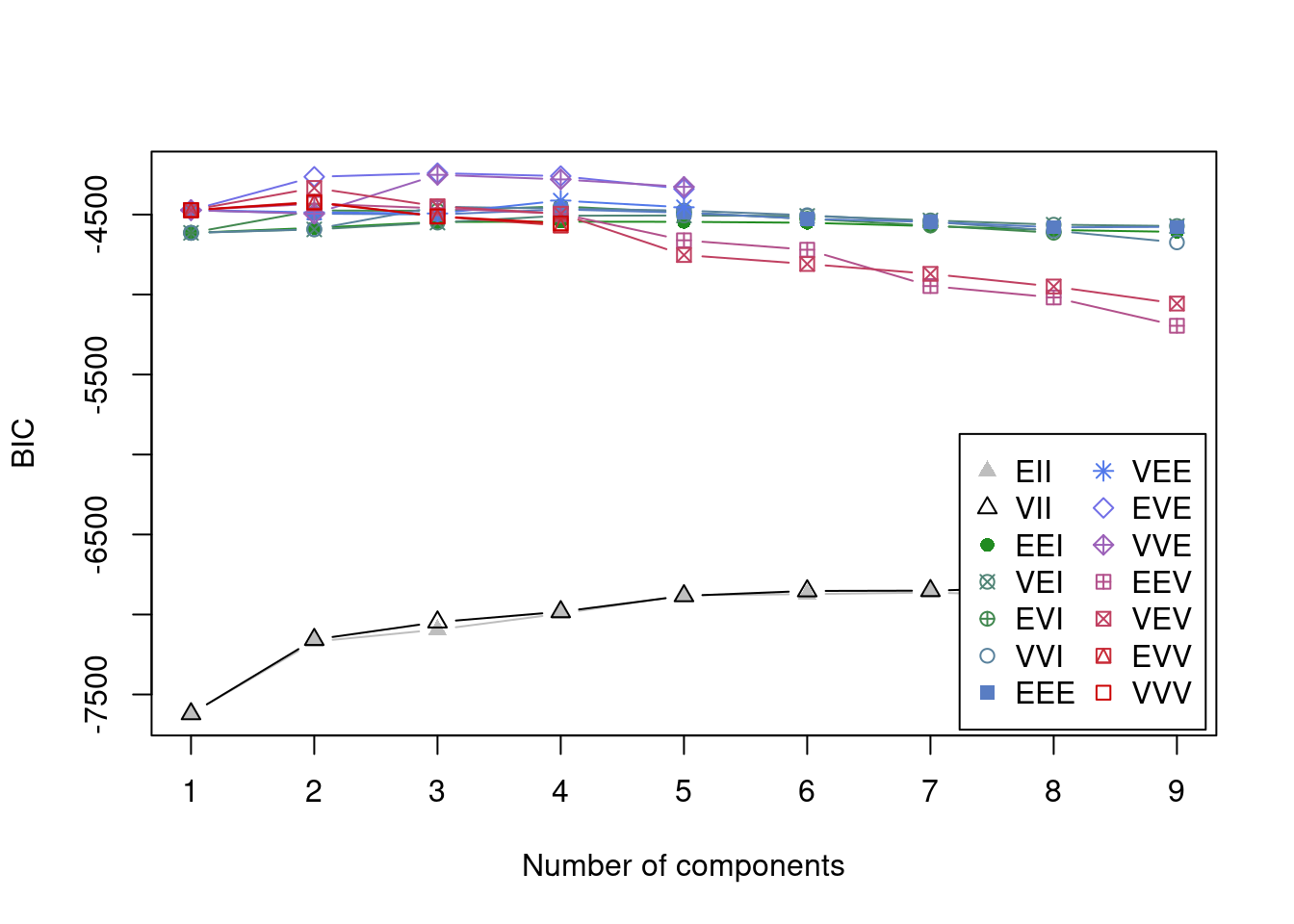
Bayesian Information Criterion (BIC):
EII VII EEI VEI EVI VVI EEE
1 -8603.643 -8603.643 -5248.673 -5248.673 -5248.673 -5248.673 -5013.525
2 -8180.746 -8145.945 -5195.004 -5179.054 -5074.935 -5188.752 -5043.922
3 -8018.775 -7958.193 -5123.311 -5123.364 -5052.693 -5045.947 -5027.830
4 -7886.718 -7809.731 -5122.158 -5084.377 -5032.702 -5041.932 -5008.398
5 -7793.774 -7768.060 -5134.493 -5098.375 -5071.128 -5069.619 -4983.409
6 -7804.335 -7710.476 -5143.886 -5064.669 -5097.344 -5086.589 -5026.058
7 -7829.608 -7750.220 -5102.629 -5089.686 -5130.281 -5148.934 -5064.913
8 -7811.437 -7690.886 -5147.698 -5107.179 NA -5152.835 -5103.672
9 -7821.009 NA -5176.384 -5135.631 -5216.412 -5210.954 -5130.004
VEE EVE VVE EEV VEV EVV VVV
1 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525
2 -4931.580 -4783.578 -4798.503 -4900.518 -4910.007 -4829.636 -4917.365
3 -4918.407 -4732.160 -4741.304 -5008.543 -4979.580 -4951.217 -4935.149
4 NA NA NA -5066.316 -5069.238 NA NA
5 NA NA NA -5190.303 -5154.202 NA NA
6 NA NA NA -5302.184 -5337.304 NA NA
7 NA NA NA -5410.215 -5488.902 NA NA
8 NA NA NA -5614.172 -5598.786 NA NA
9 NA NA NA -5810.771 -5718.486 NA NA
Top 3 models based on the BIC criterion:
EVE,3 VVE,3 EVE,2
-4732.160 -4741.304 -4783.578 Best BIC values:
EVE,3 VVE,3 EVE,2
BIC -4732.16 -4741.303592 -4783.57810
BIC diff 0.00 -9.143912 -51.41842
Code
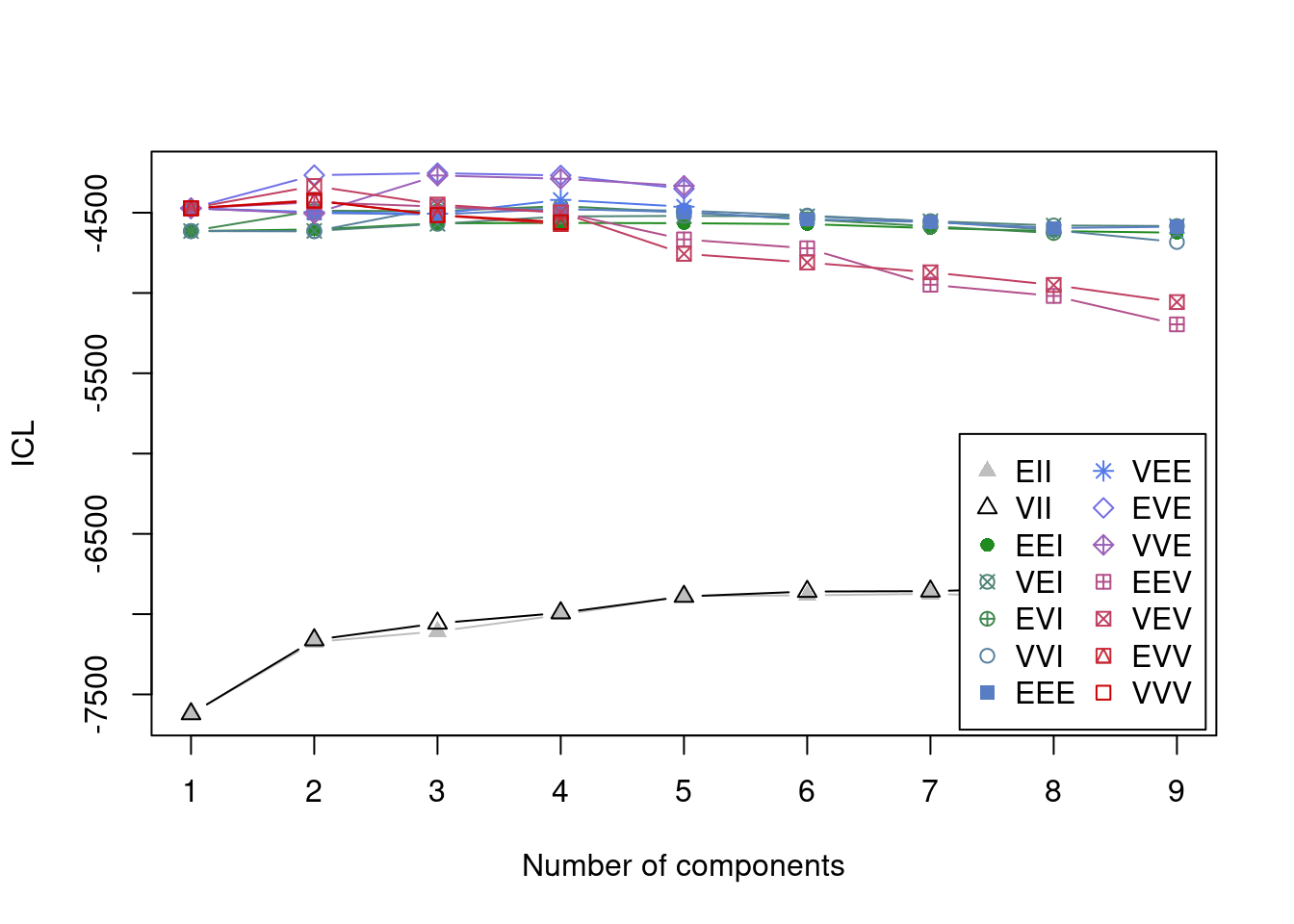
Integrated Complete-data Likelihood (ICL) criterion:
EII VII EEI VEI EVI VVI EEE
1 -8603.643 -8603.643 -5248.673 -5248.673 -5248.673 -5248.673 -5013.525
2 -8187.741 -8151.209 -5212.753 -5193.445 -5087.831 -5209.229 -5059.061
3 -8024.506 -7962.807 -5140.832 -5137.842 -5077.579 -5065.933 -5044.859
4 -7899.800 -7817.683 -5139.308 -5100.665 -5050.906 -5062.092 -5025.581
5 -7804.126 -7772.814 -5163.669 -5117.892 -5090.647 -5088.063 -4996.299
6 -7817.466 -7715.284 -5172.196 -5080.730 -5118.995 -5102.059 -5045.255
7 -7843.580 -7759.784 -5127.665 -5105.712 -5151.788 -5160.820 -5087.764
8 -7827.441 -7700.565 -5177.110 -5120.976 NA -5164.537 -5129.469
9 -7837.682 NA -5199.922 -5149.695 -5235.548 -5222.012 -5156.778
VEE EVE VVE EEV VEV EVV VVV
1 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525 -5013.525
2 -4935.604 -4789.231 -4801.418 -4900.886 -4912.682 -4830.592 -4919.755
3 -4920.143 -4751.404 -4755.780 -5011.444 -4983.537 -4956.237 -4937.699
4 NA NA NA -5073.906 -5075.676 NA NA
5 NA NA NA -5194.380 -5156.025 NA NA
6 NA NA NA -5304.374 -5340.039 NA NA
7 NA NA NA -5410.594 -5490.630 NA NA
8 NA NA NA -5614.753 -5599.162 NA NA
9 NA NA NA -5811.260 -5718.988 NA NA
Top 3 models based on the ICL criterion:
EVE,3 VVE,3 EVE,2
-4751.404 -4755.780 -4789.231 Best ICL values:
EVE,3 VVE,3 EVE,2
ICL -4751.404 -4755.780236 -4789.23090
ICL diff 0.000 -4.376279 -37.82694
Based on the cluster analyses, it appears that three clusters are the best fit to the data.
We can also use the tidyLPA package (Rosenberg et al., 2018; Rosenberg & van Lissa, 2021), which provides an interface to the mclust package (Fraley et al., 2024; Scrucca et al., 2023).
Code
# model 1 (EEI): Equal variances and covariances fixed to 0
# model 2 (VVI): Varying variances and covariances fixed to 0
# model 3 (EEE): Equal variances and equal covariances
# model 4 : Varying variances and equal covariances (not able to be fit w/ mclust but can be fit using package = "mplus", if installed)
# model 5 : Equal variances and varying covariances (not able to be fit w/ mclust but can be fit using package = "mplus", if installed)
# model 6 (VVV): Varying variances and varying covariances
wrTypes_lpa_classes <- tidyLPA::estimate_profiles(
df = merged_dataWRs_cluster %>% select(-gsis_id, -display_name),
n_profiles = 1:6,
models = c(1, 2, 3) #c(1, 2, 3, 6) takes too long to run because of the model with varying variances and varying covariances (model 6)
)
wrTypes_lpa_classestidyLPA analysis using mclust:
Model Classes AIC BIC Entropy prob_min prob_max n_min n_max BLRT_p
1 1 5197.34 5248.67 1.00 1.00 1.00 1.00 1.00
1 2 5115.15 5195.00 0.78 0.92 0.96 0.41 0.59
1 3 5014.93 5123.31 0.86 0.94 0.95 0.16 0.42
1 4 4985.26 5122.16 0.89 0.93 0.99 0.03 0.43
1 5 4969.08 5134.49 0.85 0.79 1.00 0.03 0.35
1 6 4949.95 5143.89 0.86 0.84 1.00 0.03 0.26
2 1 5197.34 5248.67 1.00 1.00 1.00 1.00 1.00
2 2 5083.23 5188.75 0.75 0.93 0.94 0.47 0.53
2 3 4886.23 5045.95 0.86 0.91 0.95 0.25 0.49
2 4 4828.03 5041.93 0.88 0.91 0.96 0.13 0.33
2 5 4801.53 5069.62 0.90 0.87 0.96 0.13 0.30
2 6 4764.31 5086.59 0.93 0.91 0.99 0.11 0.25
3 1 4859.51 5013.52 1.00 1.00 1.00 1.00 1.00
3 2 4861.39 5043.92 0.79 0.94 0.95 0.47 0.53 0.53
3 3 4816.78 5027.83 0.87 0.93 0.97 0.09 0.47 0.01
3 4 4768.83 5008.40 0.89 0.91 1.00 0.05 0.48 0.01
3 5 4715.32 4983.41 0.92 0.94 1.00 0.05 0.48 0.01
3 6 4729.45 5026.06 0.90 0.84 1.00 0.05 0.41 1.00 Code
Compare tidyLPA solutions:
Model Classes AIC BIC Entropy BLRT_p
1 1 5197.337 5248.673 1.000
1 2 5115.147 5195.004 0.782
1 3 5014.934 5123.311 0.862
1 4 4985.261 5122.158 0.891
1 5 4969.075 5134.493 0.849
1 6 4949.948 5143.886 0.858
2 1 5197.337 5248.673 1.000
2 2 5083.227 5188.752 0.755
2 3 4886.233 5045.947 0.855
2 4 4828.029 5041.932 0.876
2 5 4801.528 5069.619 0.896
2 6 4764.310 5086.589 0.927
3 1 4859.515 5013.525 1.000
3 2 4861.392 5043.922 0.792 0.535
3 3 4816.780 5027.830 0.866 0.010
3 4 4768.827 5008.398 0.890 0.010
3 5 4715.318 4983.409 0.922 0.010
3 6 4729.447 5026.058 0.901 1.000
Best model according to AIC is Model 3 with 5 classes.
Best model according to BIC is Model 3 with 5 classes.
Best model according to Entropy is Model NA with NA classes.
Best model according to BLRT_p is Model NA with NA classes.
An analytic hierarchy process, based on the fit indices AIC, AWE, BIC, CLC, and KIC (Akogul & Erisoglu, 2017), suggests the best solution is Model 3 with 5 classes.Code
tidyLPA analysis using mclust:
Model Classes AIC BIC Entropy prob_min prob_max n_min n_max BLRT_p
3 3 4816.78 5027.83 0.87 0.93 0.97 0.09 0.47 0.01 21.1.5.1.2 k-Means Clustering
Code
K-means clustering with 3 clusters of sizes 26, 39, 63
Cluster means:
vertical forty height_coalesced weight_coalesced adot.rec
1 36.09615 4.475385 72.46154 203.8077 9.776375
2 35.73077 4.491795 74.02564 210.6667 11.699977
3 36.39683 4.449206 71.77778 193.8254 10.360291
drop_percent.rec receiving_air_yards_per_rec brk_tkl.rec
1 0.04038545 14.90725 29.230769
2 0.05238580 19.61514 8.282051
3 0.05178868 17.81870 6.666667
receptions_per_season
1 82.43350
2 55.74099
3 36.71868
Clustering vector:
[1] 1 2 3 3 2 2 1 1 3 1 2 2 2 2 3 3 2 3 1 2 3 1 3 2 2 3 1 2 3 3 1 1 3 3 3 3 1
[38] 1 2 1 3 3 2 1 3 2 3 3 2 1 2 1 3 3 1 3 1 3 3 3 1 2 3 3 2 3 3 2 3 3 2 1 1 3
[75] 2 3 2 3 3 3 3 3 2 2 3 2 3 1 1 2 2 2 2 2 3 3 3 2 3 3 3 2 3 3 3 2 2 3 3 2 1
[112] 3 3 3 2 1 3 3 3 3 2 2 1 3 3 3 1 3
Within cluster sum of squares by cluster:
[1] 13865.03 16807.74 25601.52
(between_SS / total_SS = 50.3 %)
Available components:
[1] "cluster" "centers" "totss" "withinss" "tot.withinss"
[6] "betweenss" "size" "iter" "ifault" 21.1.5.2 Fit the Cluster Model to the Optimal Number of WR Types
Code
----------------------------------------------------
Gaussian finite mixture model fitted by EM algorithm
----------------------------------------------------
Mclust EVE (ellipsoidal, equal volume and orientation) model with 3 components:
log-likelihood n df BIC ICL
-2147.738 128 90 -4732.16 -4751.404
Clustering table:
1 2 3
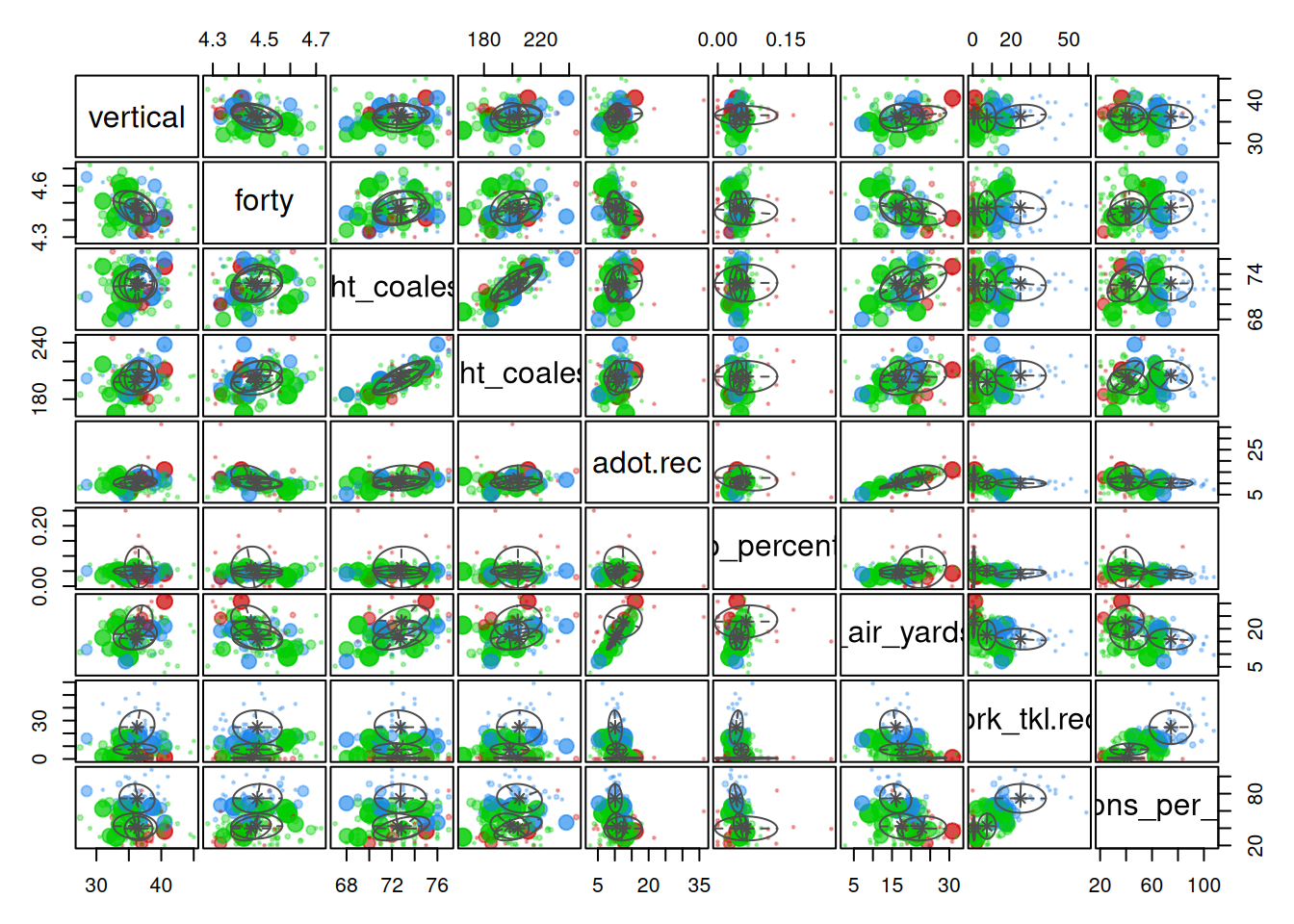
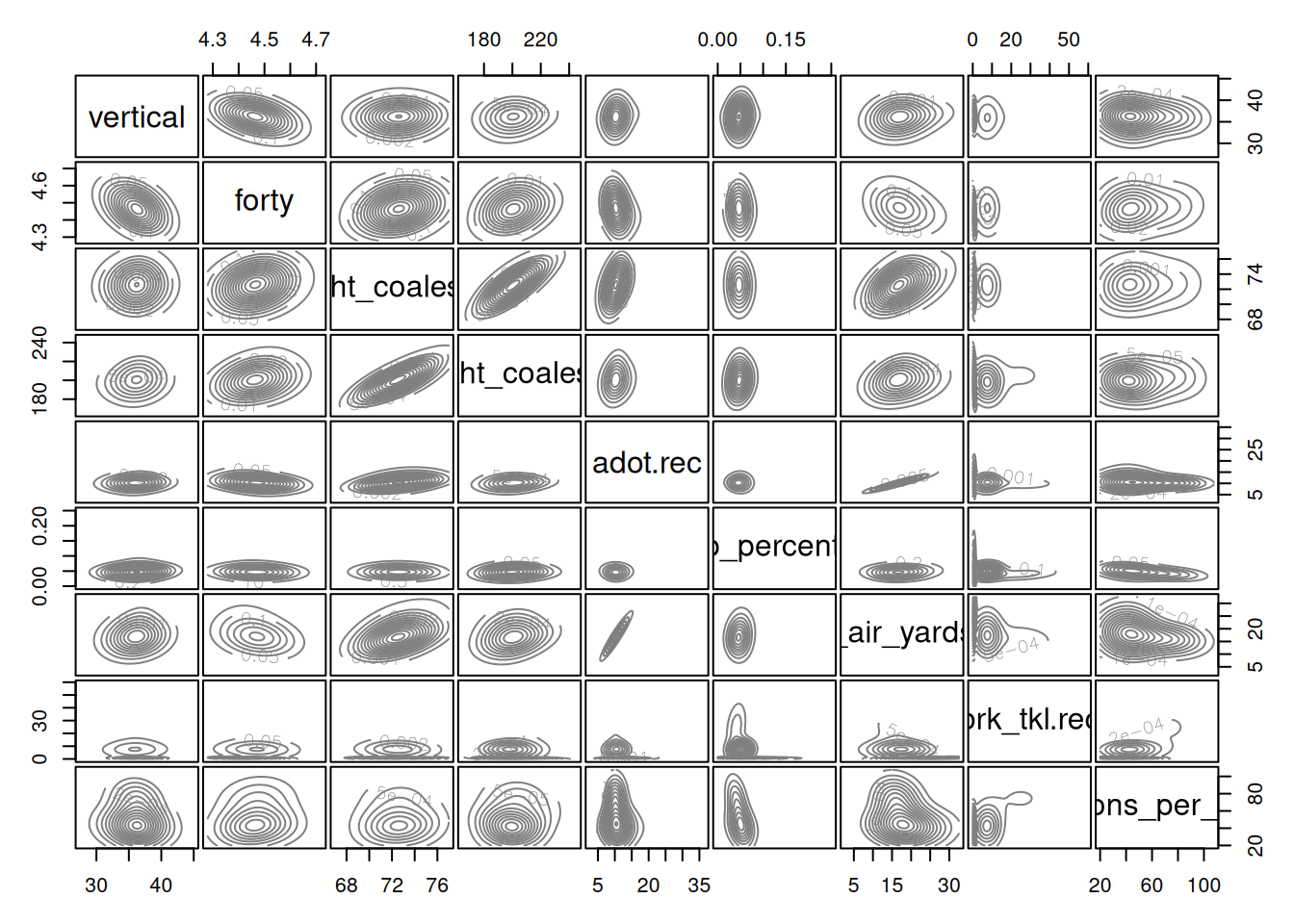
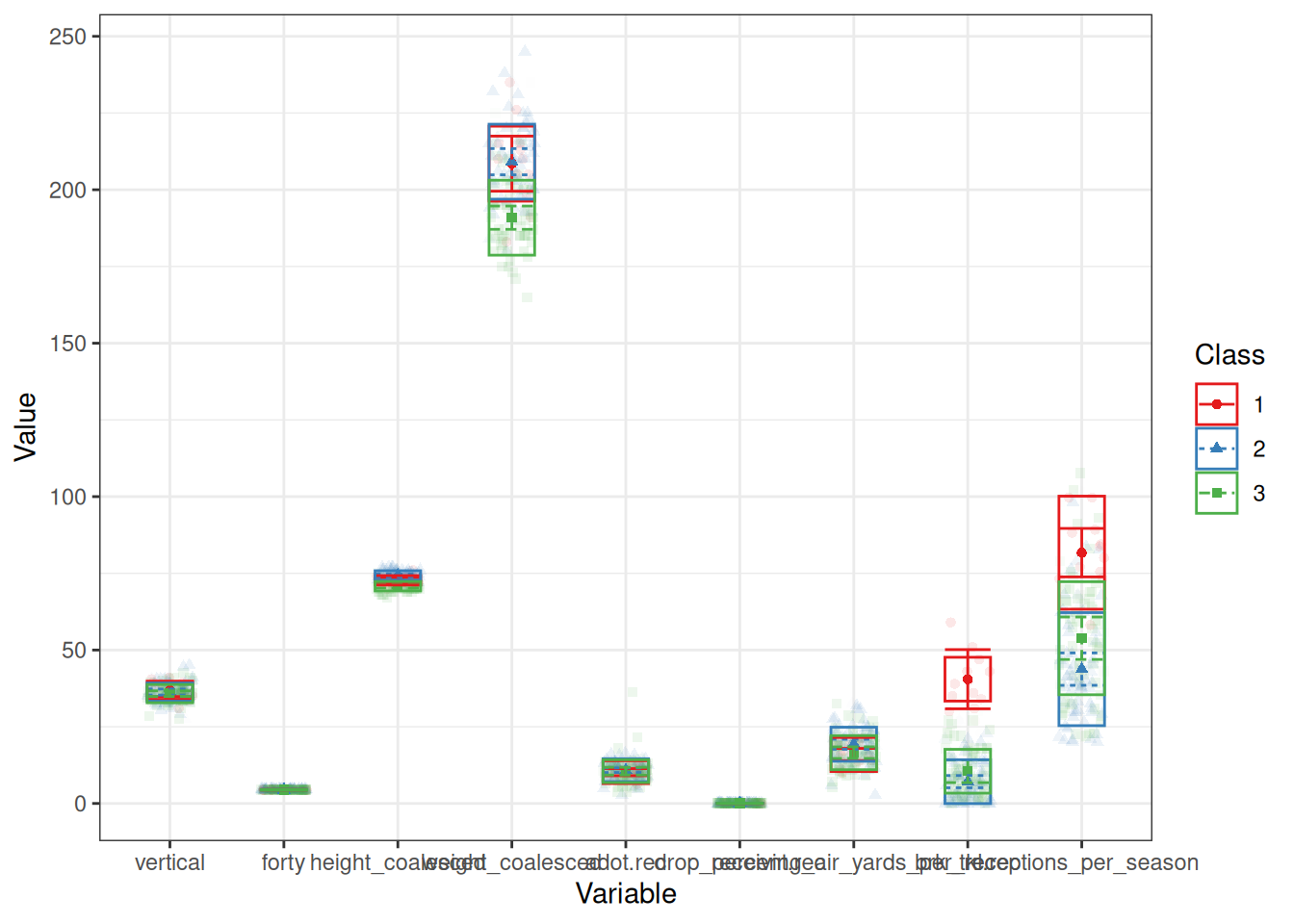
39 17 72 21.1.5.3 Plots of the Cluster Model
21.1.5.4 Interpreting the Clusters
1 2 3
39 17 72 Code
[,1] [,2] [,3]
type 1.00 2.00 3.00
vertical 36.44 36.82 35.81
forty 4.47 4.45 4.47
height_coalesced 72.74 73.06 72.42
weight_coalesced 205.67 205.53 197.38
adot.rec 10.22 12.52 10.44
drop_percent.rec 0.04 0.06 0.05
receiving_air_yards_per_rec 16.13 23.28 17.36
brk_tkl.rec 25.10 0.53 7.15
receptions_per_season 74.90 39.92 42.09Based on this analysis (and the variables included), there appear to be three types of Wide Receivers. We examined the following variables: the player’s vertical jump in the NFL Combine,40-yard-dash time in the NFL Combine, height, weight, average depth of target, drop percentage, receiving air yards per reception, broken tackles, and receptions per season.
Type 1 Wide Receivers included the Elite WR1s who are strong possession receivers (note: not all players in a given cluster map on perfectly to the typology—i.e., not all Type 1 Wide Receivers are elite WR1s). They tended to have the lowest drop percentage, the shortest average depth of target, and the fewest receiving air yards per reception. They tended to have the most receptions per season and break the most tackles.
Type 2 Wide Receivers included the consistent contributor, WR2 types. They had fewer receptions and fewer broken tackles than Type 1 Wide Receivers. Their average depth of target was longer than Type 1, and they had more receiving air yards per reception than Type 1.
Type 3 Wide Receivers included the deep threats. They had the greatest average depth of target and the most receiving yards per reception. However, they also had the fewest receptions, the highest drop percentage, and the fewest broken tackles. Thus, they may be considered the boom-or-bust Wide Receivers.
The tiers were not particularly distinguishable based on their height, weight, vertical jump, or forty-yard dash time.
Type 1 (“Elite/WR1”) WRs:
Type 2 (“Consistent Contributor/WR2”) WRs:
Type 3 (“Deep Threat/Boom-or-Bust”) WRs:
And here are the clusters based on the tidyLPA (Rosenberg et al., 2018; Rosenberg & van Lissa, 2021) solution:
Code
Code
[,1] [,2] [,3]
Class 1.00 2.00 3.00
vertical 36.96 36.30 35.78
forty 4.47 4.49 4.44
height_coalesced 72.75 74.32 70.73
weight_coalesced 208.83 209.35 190.34
adot.rec 10.26 10.84 10.53
drop_percent.rec 0.04 0.05 0.05
receiving_air_yards_per_rec 16.05 19.32 16.48
brk_tkl.rec 40.67 6.88 10.75
receptions_per_season 81.89 43.57 54.17
type 1.00 2.48 2.29
model_number 3.00 3.00 3.00
classes_number 3.00 3.00 3.00
CPROB1 0.97 0.00 0.01
CPROB2 0.01 0.94 0.05
CPROB3 0.02 0.06 0.9421.2 Conclusion
The goal of cluster analysis is to identify distinguishable subgroups of people. There are many approaches to cluster analysis, including model-based clustering, density-based clustering, centroid-based clustering, hierarchical clustering (aka connectivity-based clustering), and others. The present chapter used model-based clustering to identify tiers of players based on projected points. Using various performance metrics of Wide Receivers, we identified three subtypes of Wide Receivers: 1) Elite WR1s who are strong possession receivers; 2) Consistent Contributor/WR2s; 3) deep threats/boom-or-bust receivers. The “Elite WR1s” tended to have the lowest drop percentage, the shortest average depth of target, the fewest receiving air yards per reception, the most receptions per season, and the most broken tackles. The “Consistent Contributor/WR2s” had fewer receptions and fewer broken tackles than the Elite WR1s; their average depth of target was longer than Elite WR1s, and they had more receiving air yards per reception than Elite WR1s. The “Deep Threat/Boom-or-Bust” receivers had the greatest average depth of target and the most receiving yards per reception; however, they also had the fewest receptions, the highest drop percentage, and the fewest broken tackles. In sum, cluster analysis can be a useful way of identifying subgroups of individuals who are more similar to one another on various characteristics.
21.3 Session Info
R version 4.5.2 (2025-10-31)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.3 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
locale:
[1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
[4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
[7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
[10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
time zone: UTC
tzcode source: system (glibc)
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] lubridate_1.9.4 forcats_1.0.1 stringr_1.6.0 dplyr_1.1.4
[5] purrr_1.2.0 readr_2.1.6 tidyr_1.3.1 tibble_3.3.0
[9] tidyverse_2.0.0 plotly_4.11.0 ggplot2_4.0.1 tidyLPA_1.1.0
[13] mclust_6.1.2 nflreadr_1.5.0 petersenlab_1.2.2
loaded via a namespace (and not attached):
[1] tidyselect_1.2.1 psych_2.5.6 viridisLite_0.4.2
[4] farver_2.1.2 S7_0.2.1 lazyeval_0.2.2
[7] fastmap_1.2.0 digest_0.6.39 rpart_4.1.24
[10] timechange_0.3.0 lifecycle_1.0.4 cluster_2.1.8.1
[13] magrittr_2.0.4 compiler_4.5.2 rlang_1.1.6
[16] Hmisc_5.2-4 tools_4.5.2 yaml_2.3.11
[19] data.table_1.17.8 knitr_1.50 labeling_0.4.3
[22] texreg_1.39.4 htmlwidgets_1.6.4 mnormt_2.1.1
[25] plyr_1.8.9 RColorBrewer_1.1-3 withr_3.0.2
[28] foreign_0.8-90 nnet_7.3-20 grid_4.5.2
[31] stats4_4.5.2 lavaan_0.6-20 fastDummies_1.7.5
[34] xtable_1.8-4 colorspace_2.1-2 scales_1.4.0
[37] MASS_7.3-65 cli_3.6.5 mvtnorm_1.3-3
[40] rmarkdown_2.30 reformulas_0.4.2 generics_0.1.4
[43] rstudioapi_0.17.1 tzdb_0.5.0 httr_1.4.7
[46] reshape2_1.4.5 minqa_1.2.8 DBI_1.2.3
[49] cachem_1.1.0 pander_0.6.6 splines_4.5.2
[52] parallel_4.5.2 base64enc_0.1-3 mitools_2.4
[55] vctrs_0.6.5 boot_1.3-32 Matrix_1.7-4
[58] jsonlite_2.0.0 hms_1.1.4 Formula_1.2-5
[61] htmlTable_2.4.3 crosstalk_1.2.2 proto_1.0.0
[64] glue_1.8.0 nloptr_2.2.1 stringi_1.8.7
[67] gtable_0.3.6 quadprog_1.5-8 lme4_1.1-38
[70] pillar_1.11.1 htmltools_0.5.8.1 R6_2.6.1
[73] Rdpack_2.6.4 mix_1.0-13 evaluate_1.0.5
[76] pbivnorm_0.6.0 lattice_0.22-7 gsubfn_0.7
[79] rbibutils_2.4 backports_1.5.0 memoise_2.0.1
[82] Rcpp_1.1.0 coda_0.19-4.1 gridExtra_2.3
[85] nlme_3.1-168 checkmate_2.3.3 MplusAutomation_1.2
[88] xfun_0.54 pkgconfig_2.0.3