I want your feedback to make the book better for you and other readers. If you find typos, errors, or places where the text may be improved, please let me know. The best ways to provide feedback are by GitHub or hypothes.is annotations.
You can leave a comment at the bottom of the page/chapter, or open an issue or submit a pull request on GitHub: https://github.com/isaactpetersen/Fantasy-Football-Analytics-Textbook
Alternatively, you can leave an annotation using hypothes.is.
To add an annotation, select some text and then click the
symbol on the pop-up menu.
To see the annotations of others, click the
symbol in the upper right-hand corner of the page.
22 Factor Analysis
“All models are wrong, but some are useful.”
— George Box (1979, p. 202)
This chapter provides an overview of factor analysis, which encompasses a range of latent variable modeling approaches, including exploratory and confirmatory factor analysis.
22.1 Getting Started
22.1.1 Load Packages
22.1.2 Load Data
We created the player_stats_weekly.RData and player_stats_seasonal.RData objects in Section 4.4.3.
22.1.3 Prepare Data
22.1.3.1 Season-Averages
Code
player_stats_seasonal_avgPerGame <- player_stats_seasonal %>%
mutate(
completionsPerGame = completions / games,
attemptsPerGame = attempts / games,
passing_yardsPerGame = passing_yards / games,
passing_tdsPerGame = passing_tds / games,
passing_interceptionsPerGame = passing_interceptions / games,
sacks_sufferedPerGame = sacks_suffered / games,
sack_yards_lostPerGame = sack_yards_lost / games,
sack_fumblesPerGame = sack_fumbles / games,
sack_fumbles_lostPerGame = sack_fumbles_lost / games,
passing_air_yardsPerGame = passing_air_yards / games,
passing_yards_after_catchPerGame = passing_yards_after_catch / games,
passing_first_downsPerGame = passing_first_downs / games,
#passing_epaPerGame = passing_epa / games,
#passing_cpoePerGame = passing_cpoe / games,
passing_2pt_conversionsPerGame = passing_2pt_conversions / games,
#pacrPerGame = pacr / games
pass_40_ydsPerGame = pass_40_yds / games,
pass_incPerGame = pass_inc / games,
#pass_comp_pctPerGame = pass_comp_pct / games,
fumblesPerGame = fumbles / games
)
nfl_nextGenStats_seasonal <- nfl_nextGenStats_weekly %>%
filter(season_type == "REG") %>%
select(-any_of(c("week","season_type","player_display_name","player_position","team_abbr","player_first_name","player_last_name","player_jersey_number","player_short_name"))) %>%
group_by(player_gsis_id, season) %>%
summarise(
across(everything(),
~ mean(.x, na.rm = TRUE)),
.groups = "drop")22.1.3.2 Merge Data
22.1.3.3 Specify Variables
Code
faVars <- c(
"completionsPerGame","attemptsPerGame","passing_yardsPerGame","passing_tdsPerGame",
"passing_air_yardsPerGame","passing_yards_after_catchPerGame","passing_first_downsPerGame",
"avg_completed_air_yards","avg_intended_air_yards","aggressiveness","max_completed_air_distance",
"avg_air_distance","max_air_distance","avg_air_yards_to_sticks","passing_cpoe","pass_comp_pct",
"passer_rating","completion_percentage_above_expectation"
)22.1.3.4 Subset Data
22.1.3.5 Standardize Variables
Standardizing variables is not strictly necessary in factor analysis; however, standardization can be helpful to prevent some variables from having considerably larger variances than others.
22.2 Overview of Factor Analysis
Factor analysis involves the estimation of latent variables. Latent variables are ways of studying and operationalizing theoretical constructs that cannot be directly observed or quantified. Factor analysis is a class of latent variable models that is designated to identify the structure of a measure or set of measures, and ideally, a construct or set of constructs. It aims to identify the optimal latent structure for a group of variables. The goal of factor analysis is to identify simple, parsimonious factors that underlie the “junk” (i.e., scores filled with measurement error) that we observe.
Factor analysis encompasses two general types: confirmatory factor analysis and exploratory factor analysis. Exploratory factor analysis (EFA) is a latent variable modeling approach that is used when the researcher has no a priori hypotheses about how a set of variables is structured. EFA seeks to identify the empirically optimal-fitting model in ways that balance accuracy (i.e., variance accounted for) and parsimony (i.e., simplicity). Confirmatory factor analysis (CFA) is a latent variable modeling approach that is used when a researcher wants to evaluate how well a hypothesized model fits, and the model can be examined in comparison to alternative models. Using a CFA approach, the researcher can pit models representing two theoretical frameworks against each other to see which better accounts for the observed data.
Factor analysis involves observed (manifest) variables and unobserved (latent) factors. Factor analysis assumes that the latent factor influences the manifest variables, and the latent factor therefore reflects the common variance among the variables. A factor model potentially includes factor loadings, residuals (errors or disturbances), intercepts/means, covariances, and regression paths. When depicting a factor analysis model, rectangles represent variables we observe (i.e., manifest variables), and circles represent latent (i.e., unobserved) variables. A regression path indicates a hypothesis that one variable (or factor) influences another, and it is depicted using a single-headed arrow. The standardized regression coefficient (i.e., beta or \(\beta\)) represents the strength of association between the variables or factors. A factor loading is a regression path from a latent factor to an observed (manifest) variable. The standardized factor loading represents the strength of association between the variable and the latent factor, where conceptually, it is intended to reflect the magnitude that the latent factor influences the observed variable. A residual is variance in a variable (or factor) that is unexplained by other variables or factors. A variable’s intercept is the expected value of the variable when the factor(s) (onto which it loads) is equal to zero. A covariance is the unstandardized index of the strength of association between between two variables (or factors), and it is depicted with a double-headed arrow.
Because a covariance is unstandardized, its scale depends on the scale of the variables. The covariance between two variables is the average product of their deviations from their respective means, as in Equation 10.1. The covariance of a variable with itself is equivalent to its variance, as in Equation 10.2. By contrast, a correlation is a standardized index of the strength of association between two variables. Because a correlation is standardized (fixed between [−1,1]), its scale does not depend on the scales of the variables. Because a covariance is unstandardized, its scale depends on the scale of the variables. A covariance path between two variables represents omitted shared cause(s) of the variables. For instance, if you depict a covariance path between two variables, it means that there is a shared cause of the two variables that is omitted from the model (for instance, if the common cause is not known or was not assessed).
In factor analysis, the relation between an indicator (\(\text{X}\)) and its underlying latent factor(s) (\(\text{F}\)) can be represented with a regression formula as in Equation 22.1:
\[ X = \lambda \cdot \text{F} + \text{Item Intercept} + \text{Error Term} \tag{22.1}\]
where:
- \(\text{X}\) is the observed value of the indicator
- \(\lambda\) is the factor loading, indicating the strength of the association between the indicator and the latent factor(s)
- \(\text{F}\) is the person’s value on the latent factor(s)
- \(\text{Item Intercept}\) represents the constant term that accounts for the expected value of the indicator when the latent factor(s) are zero
- \(\text{Error Term}\) is the residual, indicating the extent of variance in the indicator that is not explained by the latent factor(s)
When the latent factors are uncorrelated, the (standardized) error term for an indicator is calculated as 1 minus the sum of squared standardized factor loadings for a given item (including cross-loadings). A cross-loading is when a variable loads onto more than one latent factor.
Factor analysis is a powerful technique to help identify the factor structure that underlies a measure or construct. However, given the extensive method variance that influences scores on measure, factor analysis (and principal component analysis) tends to extract method factors. Method factors are factors that are related to the methods being assessed rather than the construct of interest. To better estimate construct factors, it is sometimes necessary to estimate both construct and method factors.
22.3 Factor Analysis and Structural Equation Modeling
Factor analysis forms the measurement model component of a structural equation model (SEM). The measurement model is what we settle on as the estimation of each construct before we add the structural component to estimate the relations among latent variables. Basically, in a structural equation model, we add the structural component onto the measurement model. For instance, our measurement model (i.e., based on factor analyis) might be to estimate, from a set of items, three latent factors: usage, aggressiveness, and performance. Our structural model then may examine what processes (e.g., sport drink consumption or sleep) influence these latent factors, how the latent factors influence each other, and what the latent factors influence (e.g., fantasy points). SEM is confirmatory factor analysis with regression paths that specify hypothesized causal relations between the latent variables (the structural component of the model). Exploratory structural equation modeling (ESEM) is a form of SEM that allows for a combination of exploratory factor analysis and confirmatory factor analysis to estimate latent variables and the relations between them.
22.4 Path Diagrams
A key tool when designing a factor analysis or structural equation model is a conceptual depiction of the hypothesized causal processes. A path diagram depicts the hypothesized causal processes that link two or more variables. Path diagrams are an example of a causal diagram and are similar to directed acyclic graphs discussed in Section 13.6. Karch (2025a) provides a tool to create lavaan R syntax from a path analytic diagram: https://lavaangui.org.
In a path analysis diagram, rectangles represent variables we observe, and circles represent latent (i.e., unobserved) variables. Single-headed arrows indicate regression paths, where conceptually, one variable is thought to influence another variable. Double-headed arrows indicate covariance paths, where conceptually, two variables are associated for some unknown reason (i.e., an omitted shared cause).
22.5 Decisions in Factor Analysis
There are five primary decisions to make in factor analysis:
- what variables to include in the model and how to scale them
- method of factor extraction: whether to use exploratory or confirmatory factor analysis
- if using exploratory factor analysis, whether and how to rotate factors
- how many factors to retain (and what variables load onto which factors)
- how to interpret and use the factors
The answer you get can differ highly depending on the decisions you make. Below, we provide guidance for each of these decisions.
22.5.1 1. Variables to Include and their Scaling
The first decision when conducting a factor analysis is which variables to include and the scaling of those variables. What factors you extract can differ widely depending on what variables you include in the analysis. For example, if you include many variables from the same source (e.g., self-report), it is possible that you will extract a factor that represents the common variance among the variables from that source (i.e., the self-reported variables). This would be considered a method factor, which works against the goal of estimating latent factors that represent the constructs of interest (as opposed to the measurement methods used to estimate those constructs).
An additional consideration is the scaling of the variables: whether to use raw variables, standardized variables, or dividing some variables by a constant to make the variables’ variances more similar. Before performing a principal component analysis (PCA), it is generally important to ensure that the variables included in the PCA are on the same scale. PCA seeks to identify components that explain variance in the data, so if the variables are not on the same scale, some variables may contribute considerably more variance than others. A common way of ensuring that variables are on the same scale is to standardize them using, for example, z scores that have a mean of zero and standard deviation of one. By contrast, factor analysis can better accommodate variables that are on different scales.
22.5.2 2. Method of Factor Extraction
22.5.2.1 Exploratory Factor Analysis
Exploratory factor analysis (EFA) is used if you have no a priori hypotheses about the factor structure of the model, but you would like to understand the latent variables represented by your items.
EFA is partly induced from the data. You feed in the data and let the program build the factor model. You can set some parameters going in, including how to extract or rotate the factors. The factors are extracted from the data without specifying the number and pattern of loadings between the items and the latent factors (Bollen, 2002). All cross-loadings are freely estimated.
22.5.2.2 Confirmatory Factor Analysis
Confirmatory factor analysis (CFA) is used to (dis)confirm a priori hypotheses about the factor structure of the model. CFA is a test of the hypothesis. In CFA, you specify the model and ask how well this model represents the data. The researcher specifies the number, meaning, associations, and pattern of free parameters in the factor loading matrix (Bollen, 2002). A key advantage of CFA is the ability to directly compare alternative models (i.e., factor structures), which is valuable for theory testing (Strauss & Smith, 2009). For instance, you could use CFA to test whether the variance in several measures’ scores is best explained with one factor or two factors. In CFA, cross-loadings are not estimated unless the researcher specifies them.
22.5.3 3. Factor Rotation
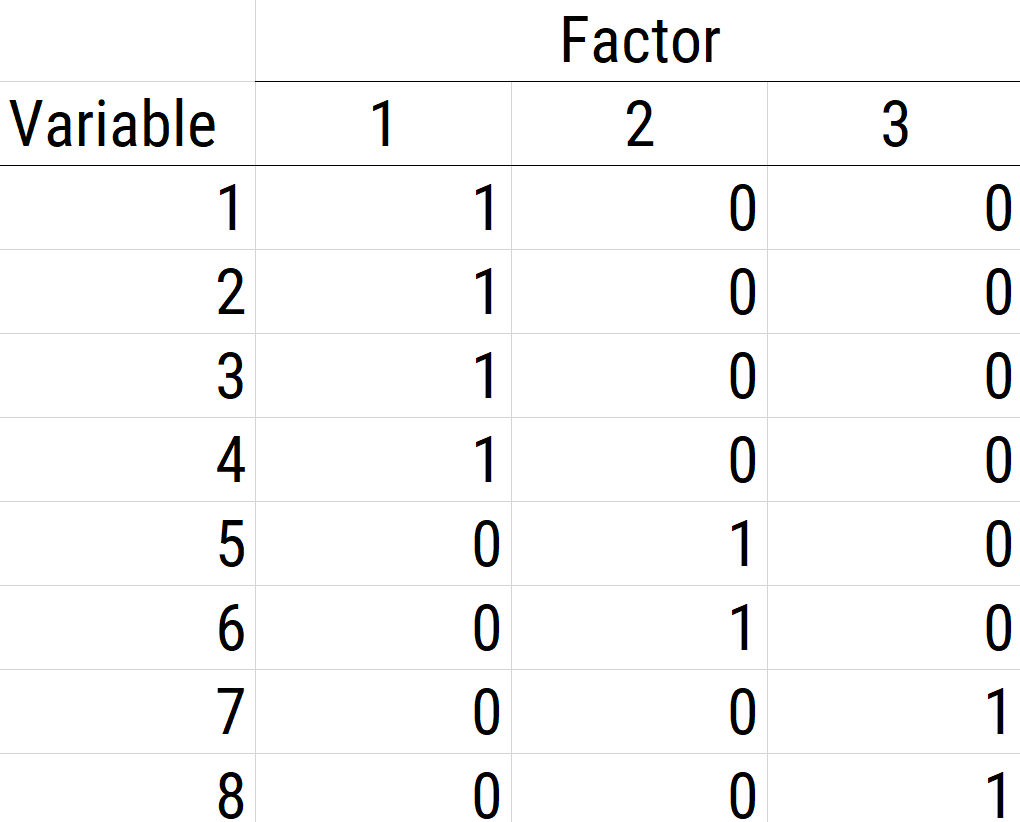
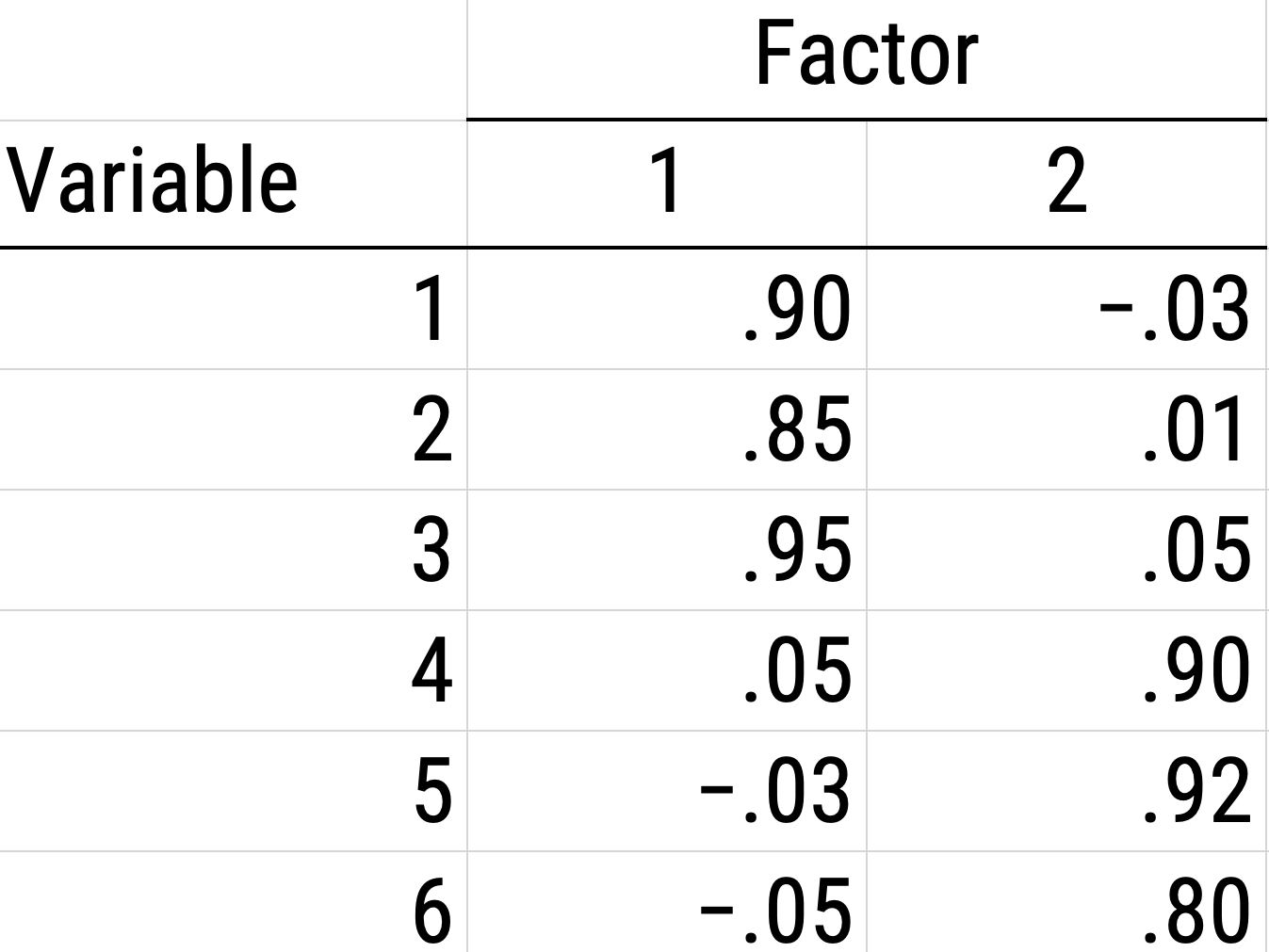
When using EFA or principal component analysis, an important step is, possibly, to rotate the factors to make them more interpretable and simple, which is the whole goal. To interpret the results of a factor analysis, we examine the factor matrix. The columns refer to the different factors; the rows refer to the different observed variables. The cells in the table are the factor loadings—they are basically the correlation between the variable and the factor. Our goal is to achieve a model with simple structure because it is easily interpretable. Simple structure means that every variable loads perfectly on one and only one factor, as operationalized by a matrix of factor loadings with values of one and zero and nothing else. An example of a factor matrix that follows simple structure is depicted in Figure 22.1.
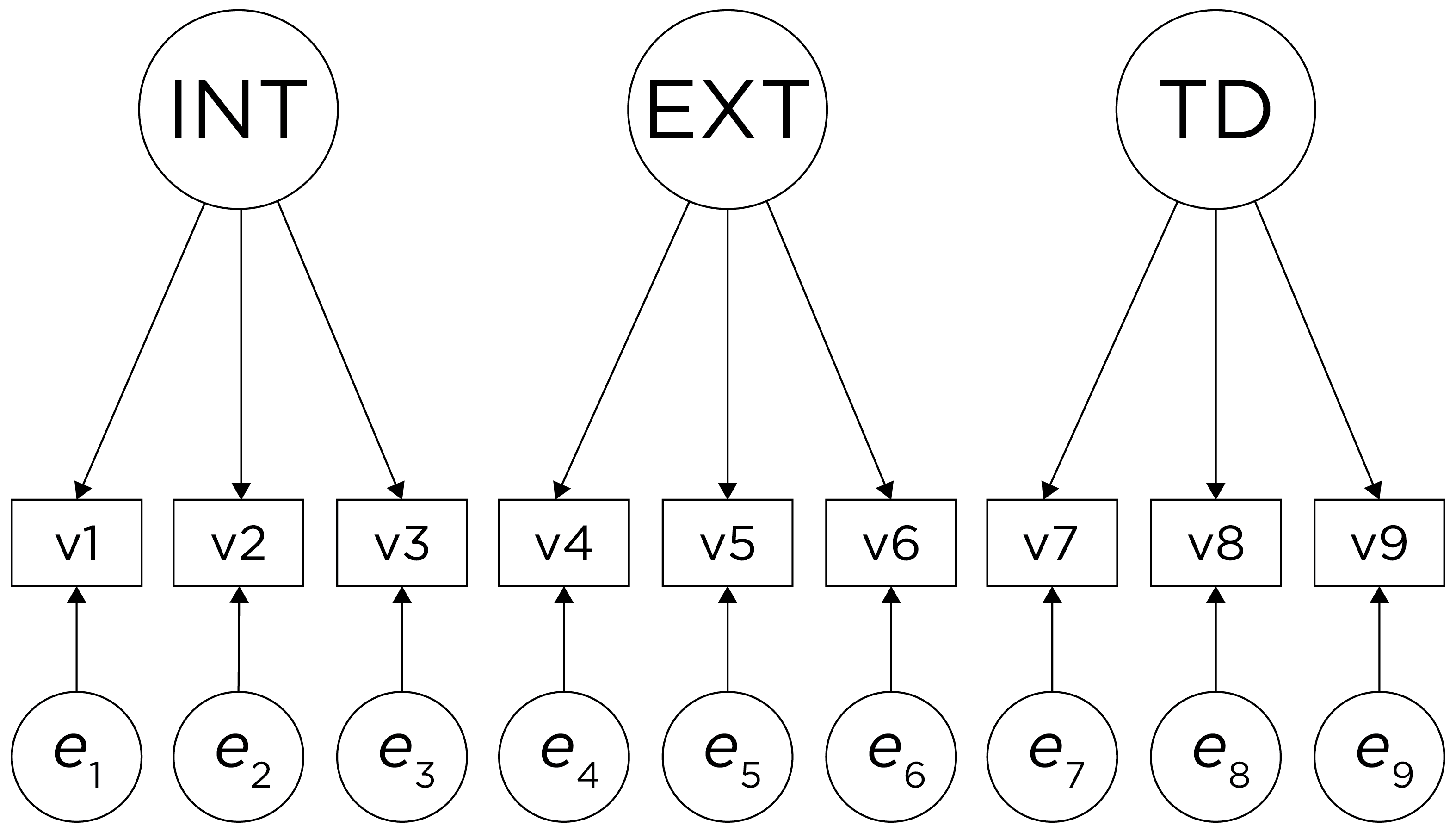
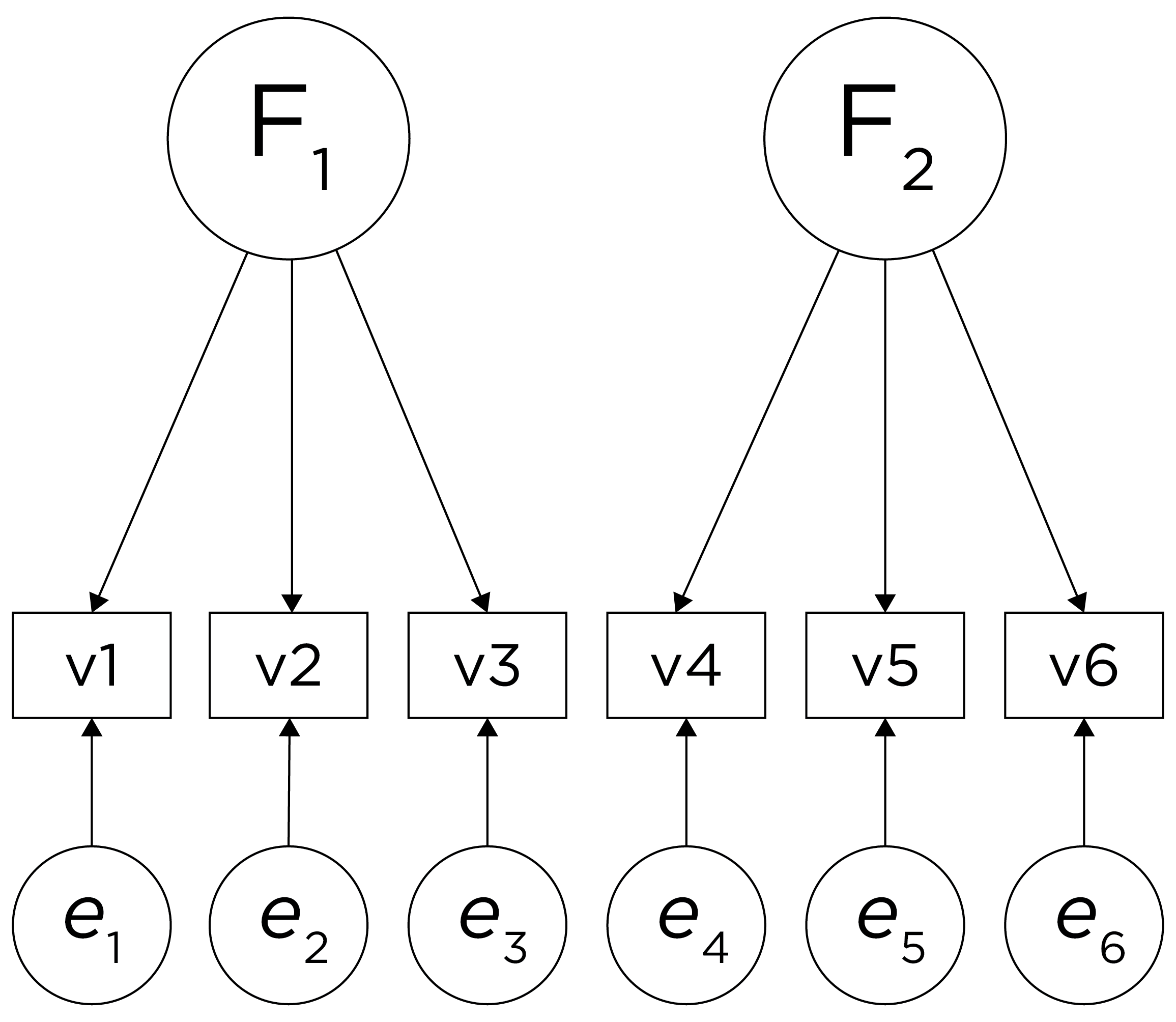
An example of a factor analysis model that follows simple structure is depicted in Figure 22.2. Each variable loads onto one and only one factor, which makes it easy to interpret the meaning of each factor, because a given factor represents the common variance among the items that load onto it.
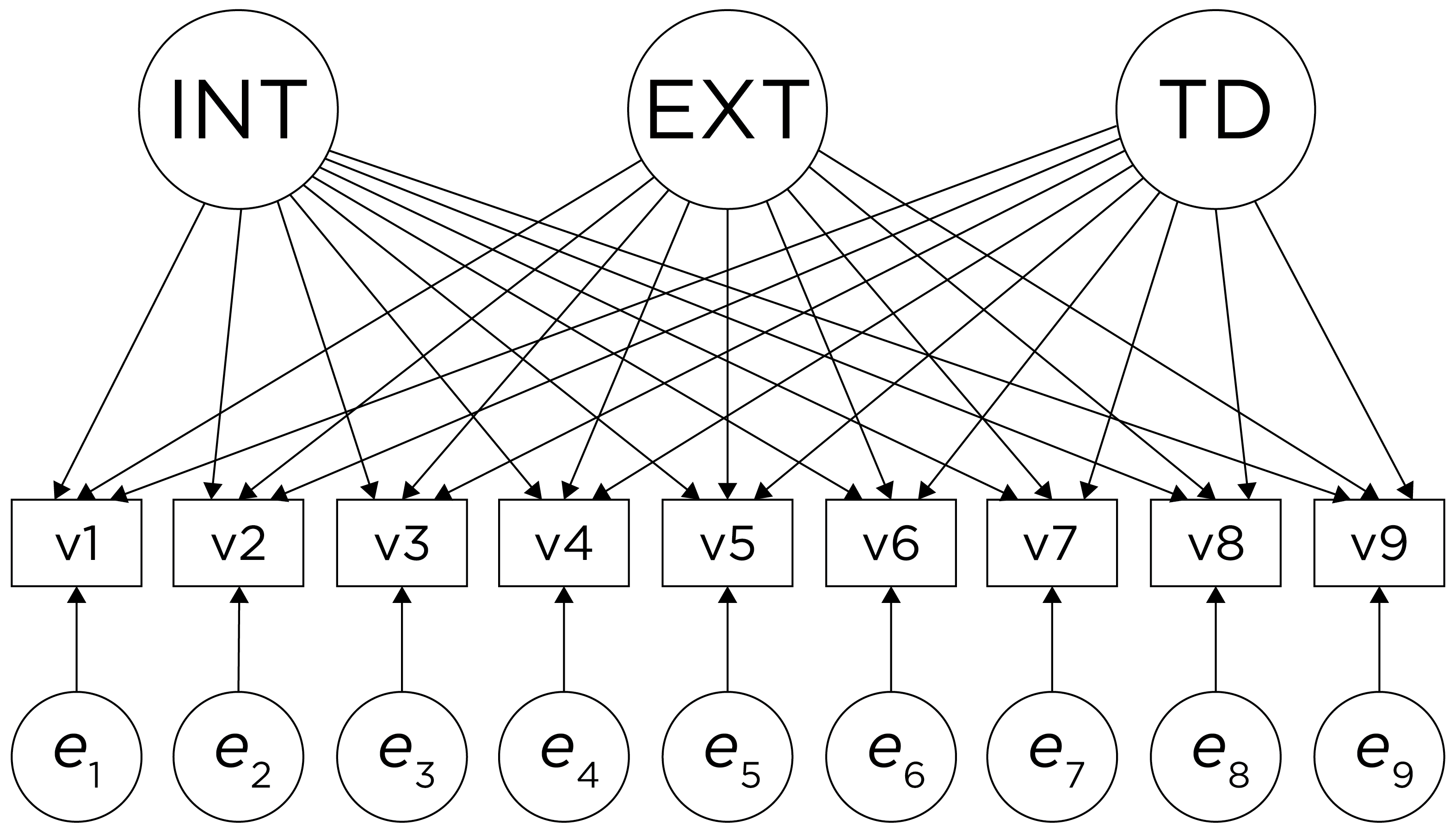
However, pure simple structure only occurs in simulations, not in real-life data. In reality, our unrotated factor analysis model might look like the model in Figure 22.3. In this example, the factor analysis model does not show simple structure because the items have cross-loadings—that is, the items load onto more than one factor. The cross-loadings make it difficult to interpret the factors, because all of the items load onto all of the factors, so the factors are not very distinct from each other, which makes it difficult to interpret what the factors mean.
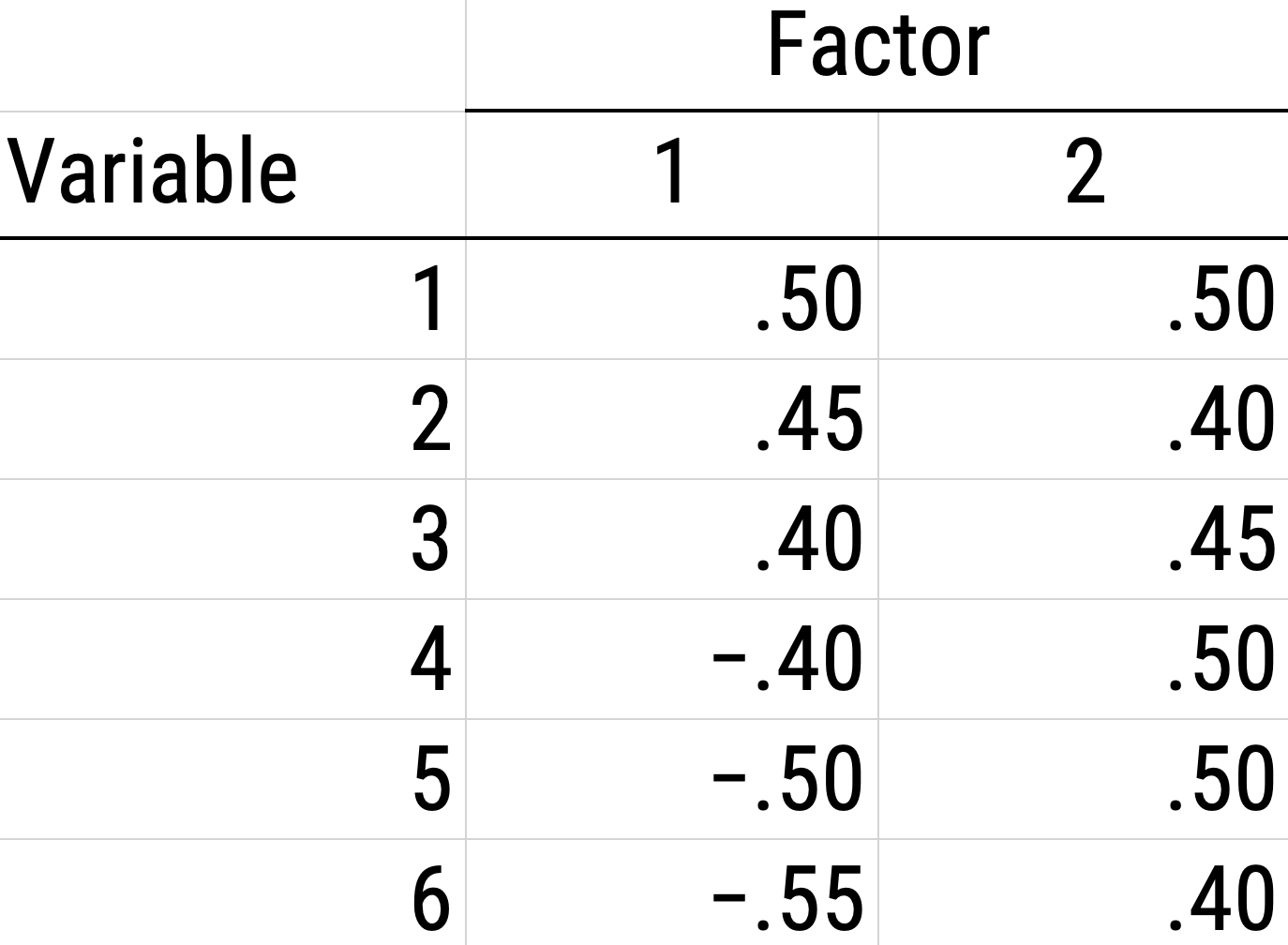
As a result of the challenges of interpretability caused by cross-loadings, factor rotations are often performed. An example of an unrotated factor matrix is in Figure 22.4.
In the example factor matrix in Figure 22.5, the factor analysis is not very helpful—it tells us very little because it did not distinguish between the two factors. The variables have similar loadings on Factor 1 and Factor 2. An example of a unrotated factor solution is in Figure 22.5. In the figure, all of the variables are in the midst of the quadrants—they are not on the factors’ axes. Thus, the factors are not very informative.
As a result, to improve the interpretability of the factor analysis, we can do what is called rotation. Rotation leverages the idea that there are infinite solutions to the factor analysis model that fit equally well. Rotation involves changing the orientation of the factors by changing the axes so that variables end up with very high (close to one or negative one) or very low (close to zero) loadings, so that it is clear which factors include which variables. That is, rotation rescales the factors and tries to identify the ideal solution (factor) for each variable. It searches for simple structure and keeps searching until it finds a minimum. After rotation, if the rotation was successful for imposing simple structure, each factor will have loadings close to one (or negative one) for some variables and close to zero for other variables. The goal of factor rotation is to achieve simple structure, to help make it easier to interpret the meaning of the factors.
To perform factor rotation, orthogonal rotations are often used. Orthogonal rotations make the rotated factors uncorrelated. An example of a commonly used orthogonal rotation is varimax rotation. Varimax rotation maximizes the sum of the variance of the squared loadings (i.e., so that items have either a very high or very low loading on a factor) and yields axes with a 90-degree angle.
An example of a factor matrix following an orthogonal rotation is depicted in Figure 22.6. An example of a factor solution following an orthogonal rotation is depicted in Figure 22.7.
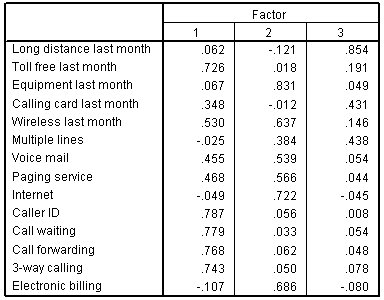
An example of a factor matrix from SPSS following an orthogonal rotation is depicted in Figure 22.8.
An example of a factor structure from an orthogonal rotation is in Figure 22.9.
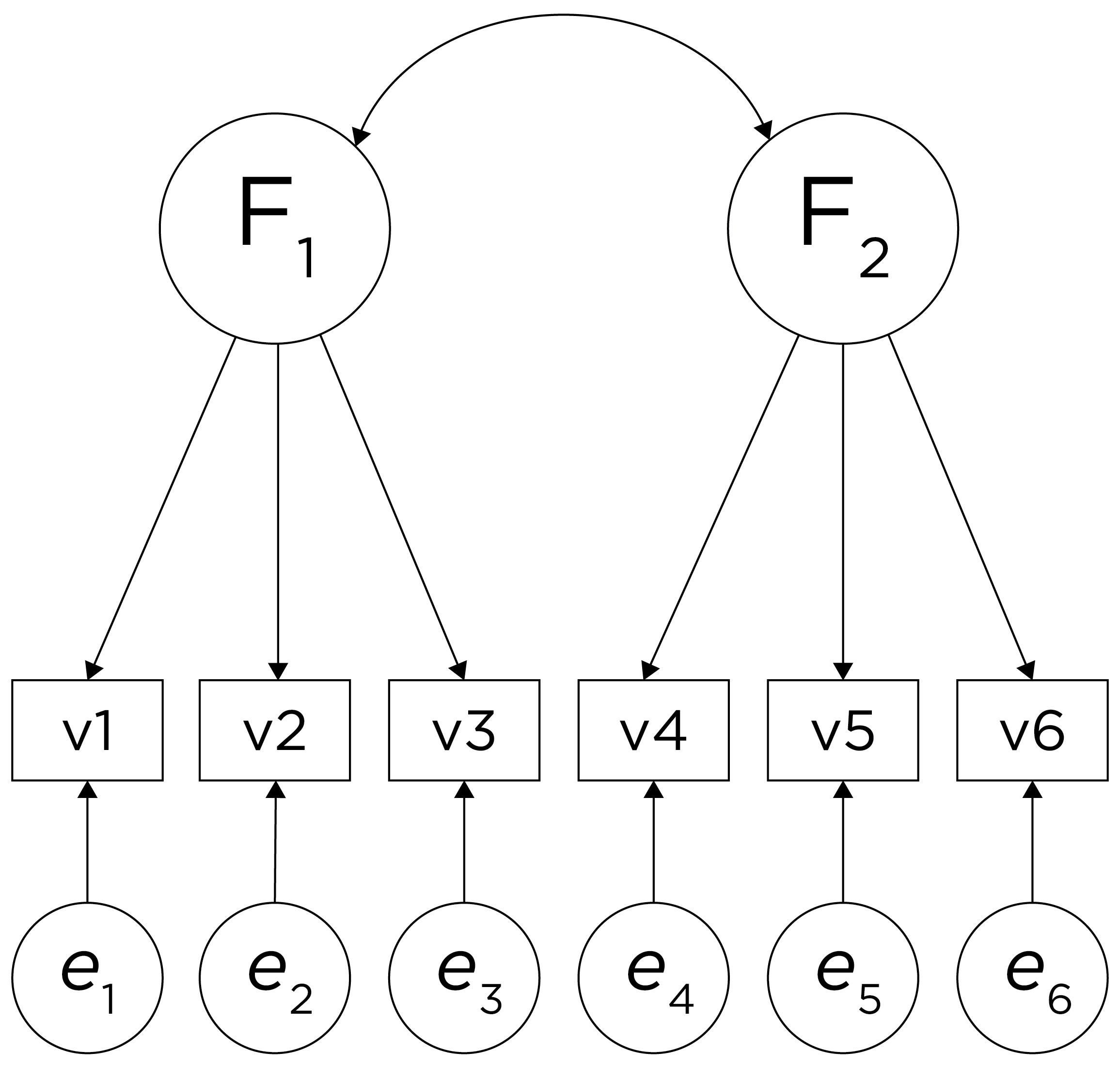
Sometimes, however, the two factors and their constituent variables may be correlated. Examples of two correlated factors may be depression and anxiety. When the two factors are correlated in reality, if we make them uncorrelated, this would result in an inaccurate model. Oblique rotation allows for factors to be correlated and yields axes with less an angle of less than 90 degrees. However, if the factors have low correlation (e.g., .2 or less), you can likely continue with orthogonal rotation. Nevertheless, just because an oblique rotation allows for correlated factors does not mean that the factors will be correlated, so oblique rotation provides greater flexibility than orthogonal rotation. An example of a factor structure from an oblique rotation is in Figure 22.10. Results from an oblique rotation are more complicated than orthogonal rotation—they provide lots of output and are more complicated to interpret. In addition, oblique rotation might not yield a smooth answer if you have a relatively small sample size.
As an example of rotation based on interpretability, consider the Five-Factor Model of Personality (the Big Five), which goes by the acronym, OCEAN: Openness, Conscientiousness, Extraversion, Agreeableness, and Neuroticism. Although the five factors of personality are somewhat correlated, we can use rotation to ensure they are maximally independent. Upon rotation, extraversion and neuroticism are essentially uncorrelated, as depicted in Figure 22.11. The other pole of extraversion is intraversion and the other pole of neuroticism might be emotional stability or calmness.
Simple structure is achieved when each variable loads highly onto as few factors as possible (i.e., each item has only one significant or primary loading). Oftentimes this is not the case, so we choose our rotation method in order to decide if the factors can be correlated (an oblique rotation) or if the factors will be uncorrelated (an orthogonal rotation). If the factors are not correlated with each other, use an orthogonal rotation. The correlation between an item and a factor is a factor loading, which is simply a way to ask how much a variable is correlated with the underlying factor. However, its interpretation is more complicated if there are correlated factors!
An orthogonal rotation (e.g., varimax) can help with simplicity of interpretation because it seeks to yield simple structure without cross-loadings. Cross-loadings are instances where a variable loads onto multiple factors. My recommendation would always be to use an orthogonal rotation if you have reason to believe that finding simple structure in your data is possible; otherwise, the factors are extremely difficult to interpret—what exactly does a cross-loading even mean? However, you should always try an oblique rotation, too, to see how strongly the factors are correlated. Examples of oblique rotations include oblimin and promax.
22.5.4 4. Determining the Number of Factors to Retain
A goal of factor analysis and principal component analysis is simplification or parsimony, while still explaining as much variance as possible. The hope is that you can have fewer factors that explain the associations between the variables than the number of observed variables. It does not make sense to replace 18 variables with 18 latent factors because that would not result in any simplification. But how do you decide on the number of factors?
There are a number of criteria that one can use to help determine how many factors/components to keep:
- Kaiser-Guttman criterion: factors with eigenvalues greater than zero
- or, for principal component analysis, components with eigenvalues greater than 1
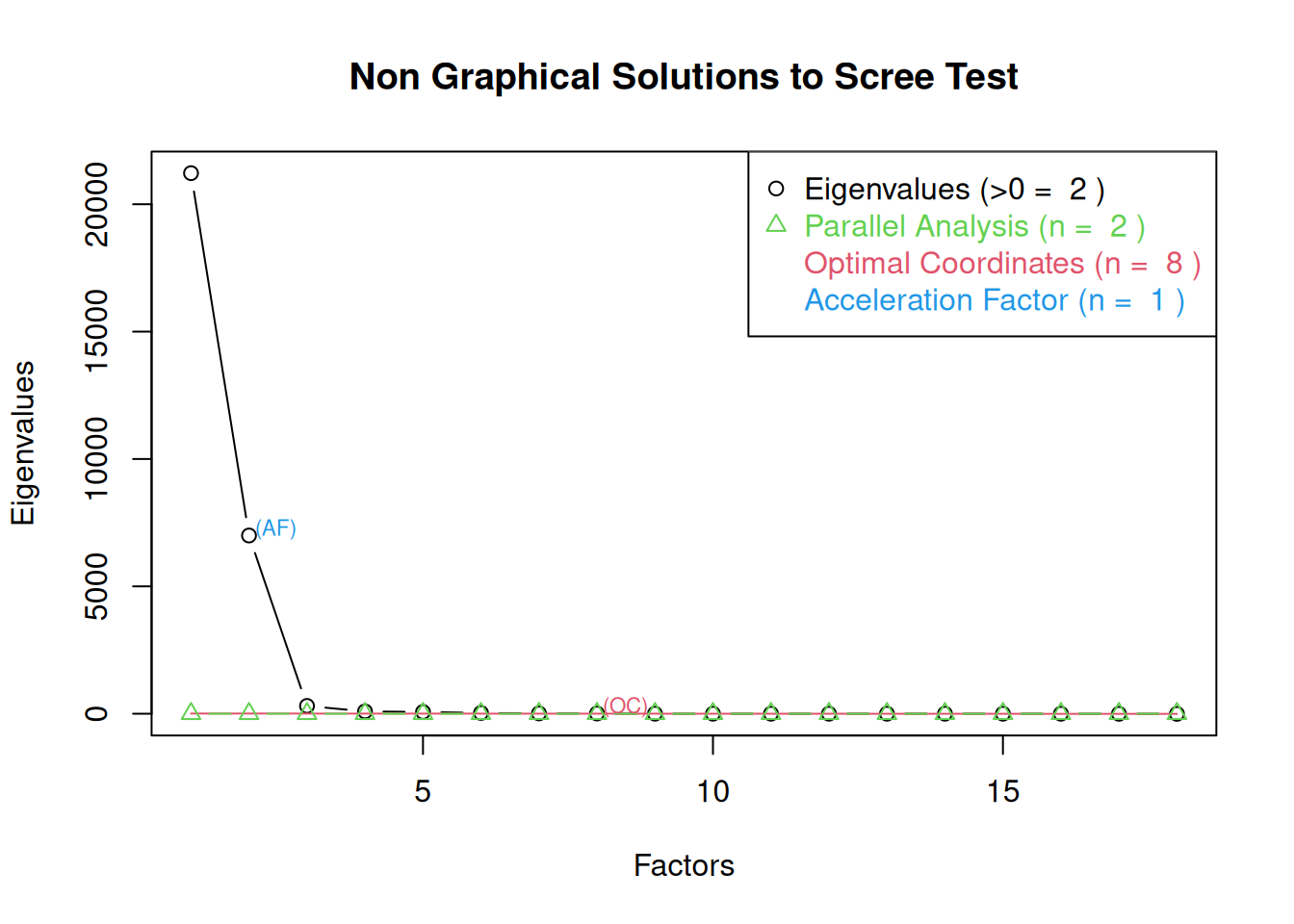
- Cattell’s scree test: the “elbow” in a scree plot minus one; sometimes operationalized with optimal coordinates (OC) or the acceleration factor (AF)
- Parallel analysis: factors that explain more variance than randomly simulated data
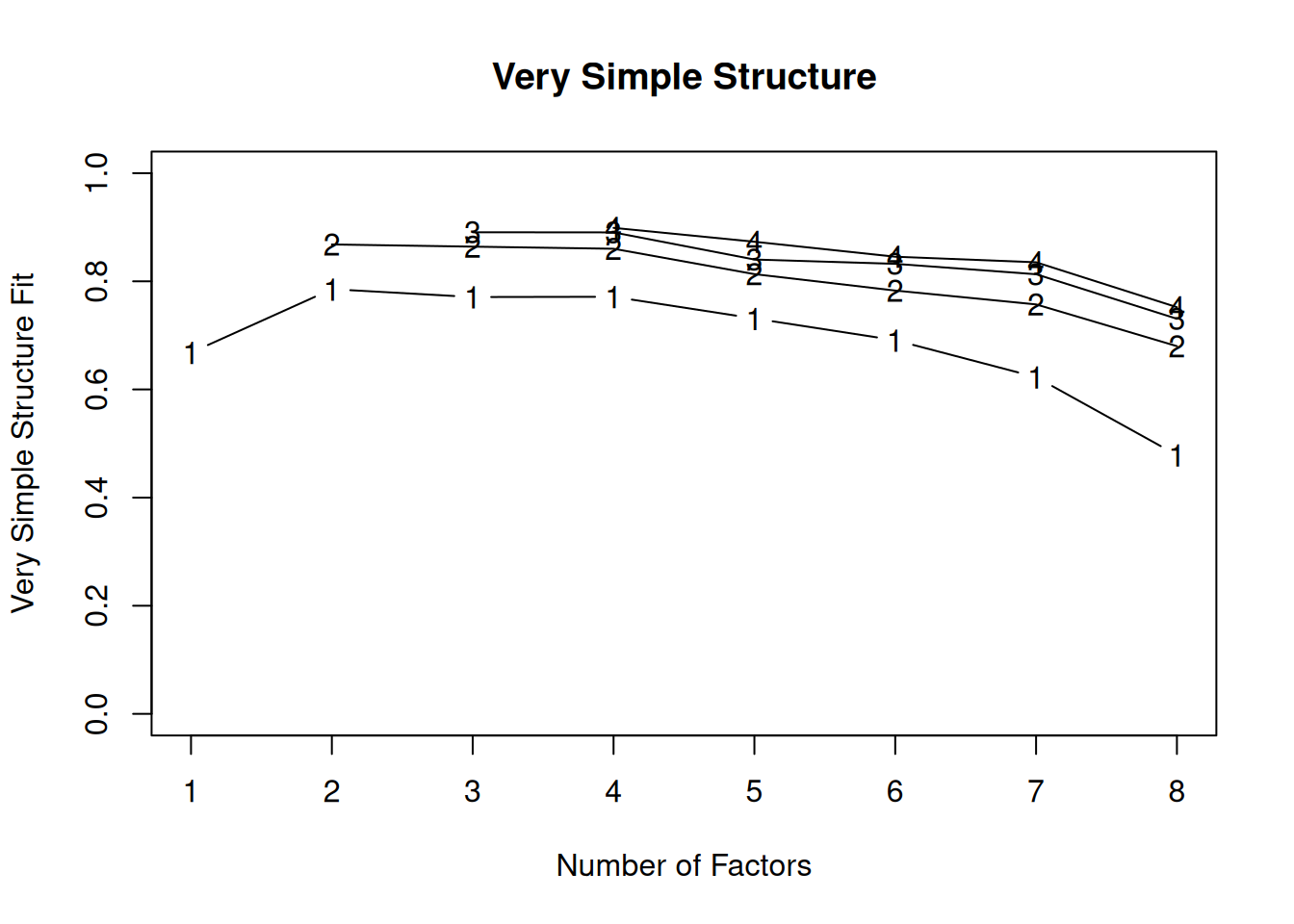
- Very simple structure (VSS) criterion: larger is better
- Velicer’s minimum average partial (MAP) test: smaller is better
- Akaike information criterion (AIC): smaller is better
- Bayesian information criterion (BIC): smaller is better
- Sample size-adjusted BIC (SABIC): smaller is better
- Root mean square error of approximation (RMSEA): smaller is better
- Chi-square difference test: smaller is better; a significant test indicates that the more complex model is significantly better fitting than the less complex model
- Standardized root mean square residual (SRMR): smaller is better
- Comparative Fit Index (CFI): larger is better
- Tucker Lewis Index (TLI): larger is better
There is not necessarily a “correct” criterion to use in determining how many factors to keep, so it is generally recommended that researchers use multiple criteria in combination with theory and interpretability.
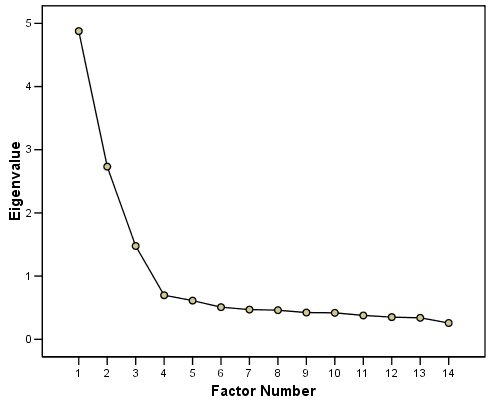
A scree plot provides lots of information. A scree plot has the factor number on the x-axis and the eigenvalue on the y-axis. The eigenvalue is the variance accounted for by a factor; when using a varimax (orthogonal) rotation, an eigenvalue (or factor variance) is calculated as the sum of squared standardized factor (or component) loadings on that factor. An example of a scree plot is in Figure 22.12.
The total variance is equal to the number of variables you have, so one eigenvalue is approximately one variable’s worth of variance. The first factor accounts for the most variance, the second factor accounts for the second-most variance, and so on. The more factors you add, the less variance is explained by the additional factor.
One criterion for how many factors to keep is the Kaiser-Guttman criterion. According to the Kaiser-Guttman criterion, you should keep any factors whose eigenvalue is greater than 1. That is, for the sake of simplicity, parsimony, and data reduction, you should take any factors that explain more than a single variable would explain. According to the Kaiser-Guttman criterion, we would keep three factors from Figure 22.12 that have eigenvalues greater than 1. The default in SPSS is to retain factors with eigenvalues greater than 1. However, keeping factors whose eigenvalue is greater than 1 is not the most correct rule. If you let SPSS do this, you may get many factors with eigenvalues around 1 (e.g., factors with an eigenvalue ~ 1.0001) that are not adding so much that it is worth the added complexity. The Kaiser-Guttman criterion usually results in keeping too many factors. Factors with small eigenvalues around 1 could reflect error shared across variables. For instance, factors with small eigenvalues could reflect method variance (i.e., method factor), such as a self-report factor that turns up as a factor in factor analysis, but that may be useless to you as a conceptual factor of a construct of interest.
Another criterion is Cattell’s scree test, which involves selecting the number of factors from looking at the scree plot. “Scree” refers to the rubble of stones at the bottom of a mountain. According to Cattell’s scree test, you should keep the factors before the last steep drop in eigenvalues—i.e., the factors before the rubble, where the slope approaches zero. The beginning of the scree (or rubble), where the slope approaches zero, is called the “elbow” of a scree plot. Using Cattell’s scree test, you retain the number of factors that explain the most variance prior to the explained variance drop-off, because, ultimately, you want to include only as many factors in which you gain substantially more by the inclusion of these factors. That is, you would keep the number of factors at the elbow of the scree plot minus one. If the last steep drop occurs from Factor 4 to Factor 5 and the elbow is at Factor 5, we would keep four factors. In Figure 22.12, the last steep drop in eigenvalues occurs from Factor 3 to Factor 4; the elbow of the scree plot occurs at Factor 4. We would keep the number of factors at the elbow minus one. Thus, using Cattell’s scree test, we would keep three factors based on Figure 22.12.
There are more sophisticated ways of using a scree plot, but they usually end up at a similar decision. Examples of more sophisticated tests include parallel analysis and very simple structure (VSS) plots. In a parallel analysis, you examine where the eigenvalues from observed data and random data converge, so you do not retain a factor that explains less variance than would be expected by random chance. Using the VSS criterion, the optimal number of factors to retain is the number of factors that maximizes the VSS criterion (Revelle & Rocklin, 1979). The VSS criterion is evaluated with models in which factor loadings for a given item that are less than the maximum factor loading for that item are suppressed to zero, thus forcing simple structure (i.e., no cross-loadings). The goal is finding a factor structure with interpretability so that factors are clearly distinguishable. Thus, we want to identify the number of factors with the highest VSS criterion.
In general, my recommendation is to use Cattell’s scree test, and then test the factor solutions with plus or minus one factor, in addition to examining model fit. You should never accept factors with eigenvalues less than zero (or components from PCA with eigenvalues less than one), because they are likely to be largely composed of error. If you are using maximum likelihood factor analysis, you can compare the fit of various models with model fit criteria to see which model fits best for its parsimony. A model will always fit better when you add additional parameters or factors, so you examine if there is significant improvement in model fit when adding the additional factor—that is, we keep adding complexity until additional complexity does not buy us much. Always try a factor solution that is one less and one more than suggested by Cattell’s scree test to buffer your final solution because the purpose of factor analysis is to explain things and to have interpretability. Even if all rules or indicators suggest to keep X number of factors, maybe \(\pm\) one factor helps clarify things. Even though factor analysis is empirical, theory and interpretatability should also inform decisions.
22.5.4.1 Model Fit Indices
In factor analysis, we fit a model to observed data, or to the variance-covariance matrix, and we evaluate the degree of model misfit. That is, fit indices evaluate how likely it is that a given causal model gave rise to the observed data. Various model fit indices can be used for evaluating how well a model fits the data and for comparing the fit of two competing models. Fit indices known as absolute fit indices compare whether the model fits better than the best-possible fitting model (i.e., a saturated model). Examples of absolute fit indices include the chi-square test, root mean square error of approximation (RMSEA), and the standardized root mean square residual (SRMR).
The chi-square test evaluates whether the model has a significant degree of misfit relative to the best-possible fitting model (a saturated model that fits as many parameters as possible; i.e., as many parameters as there are degrees of freedom); the null hypothesis of a chi-square test is that there is no difference between the predicted data (i.e., the data that would be observed if the model were true) and the observed data. Thus, a non-significant chi-square test indicates good model fit. However, because the null hypothesis of the chi-square test is that the model-implied covariance matrix is exactly equal to the observed covariance matrix (i.e., a model of perfect fit), this may be an unrealistic comparison. Models are simplifications of reality, and our models are virtually never expected to be a perfect description of reality. Thus, we would say a model is “useful” and partially validated if “it helps us to understand the relation between variables and does a ‘reasonable’ job of matching the data…A perfect fit may be an inappropriate standard, and a high chi-square estimate may indicate what we already know—that the hypothesized model holds approximately, not perfectly.” (Bollen, 1989, p. 268). The power of the chi-square test depends on sample size, and a large sample will likely detect small differences as significantly worse than the best-possible fitting model (Bollen, 1989).
RMSEA is an index of absolute fit. Lower values indicate better fit.
SRMR is an index of absolute fit with no penalty for model complexity. Lower values indicate better fit.
There are also various fit indices known as incremental, comparative, or relative fit indices that compare whether the model fits better than the worst-possible fitting model (i.e., a “baseline” or “null” model). Incremental fit indices include a chi-square difference test, the comparative fit index (CFI), and the Tucker-Lewis index (TLI). Unlike the chi-square test comparing the model to the best-possible fitting model, a significant chi-square test of the relative fit index indicates better fit—i.e., that the model fits better than the worst-possible fitting model.
CFI is another relative fit index that compares the model to the worst-possible fitting model. Higher values indicate better fit.
TLI is another relative fit index. Higher values indicate better fit.
Parsimony fit include fit indices that use information criteria fit indices, including the Akaike Information Criterion (AIC) and the Bayesian Information Criterion (BIC). BIC penalizes model complexity more so than AIC. Lower AIC and BIC values indicate better fit.
Chi-square difference tests and CFI can be used to compare two nested models. AIC and BIC can be used to compare two non-nested models.
Criteria for acceptable fit and good fit of SEM models are in Table 22.1. In addition, dynamic fit indexes have been proposed based on simulation to identify fit index cutoffs that are tailored to the characteristics of the specific model and data (McNeish & Wolf, 2023); dynamic fit indexes are available via the dynamic package (Wolf & McNeish, 2022) or with a webapp.
| SEM Fit Index | Acceptable Fit | Good Fit |
|---|---|---|
| RMSEA | \(\leq\) .08 | \(\leq\) .05 |
| CFI | \(\geq\) .90 | \(\geq\) .95 |
| TLI | \(\geq\) .90 | \(\geq\) .95 |
| SRMR | \(\leq\) .10 | \(\leq\) .08 |
However, good model fit does not necessarily indicate a true model.
In addition to global fit indices, it can also be helpful to examine evidence of local fit, such as the residual covariance matrix. The residual covariance matrix represents the difference between the observed covariance matrix and the model-implied covariance matrix (the observed covariance matrix minus the model-implied covariance matrix). These difference values are called covariance residuals. Standardizing the covariance matrix by converting each to a correlation matrix can be helpful for interpreting the magnitude of any local misfit. This is known as a residual correlation matrix, which is composed of correlation residuals. Correlation residuals greater than |.10| are possible evidence for poor local fit (Kline, 2023). If a correlation residual is positive, it suggests that the model underpredicts the observed association between the two variables (i.e., the observed covariance is greater than the model-implied covariance). If a correlation residual is negative, it suggests that the model overpredicts their observed association between the two variables (i.e., the observed covariance is smaller than the model-implied covariance). If the two variables are connected by only indirect pathways, it may be helpful to respecify the model with direct pathways between the two variables, such as a direct effect (i.e., regression path) or a covariance path. For guidance on evaluating local fit, see Kline (2024).
22.5.5 5. Interpreting and Using Latent Factors
The next step is interpreting the model and latent factors. One data matrix can lead to many different (correct) models—you must choose one based on the factor structure and theory. Use theory to interpret the model and label the factors. In latent variable models, factors have meaning. You can use them as predictors, mediators, moderators, or outcomes. When possible, it is preferable to use the factors by examining their associations with other variables in the same model. You can extract factor scores, if necessary, for use in other analyses; however, it is preferable to examine the associations between factors and other variables in the same model if possible. And, using latent factors helps disattenuate associations for measurement error, to identify what the association is between variables when removing random measurement error.
22.6 Example of Exploratory Factor Analysis
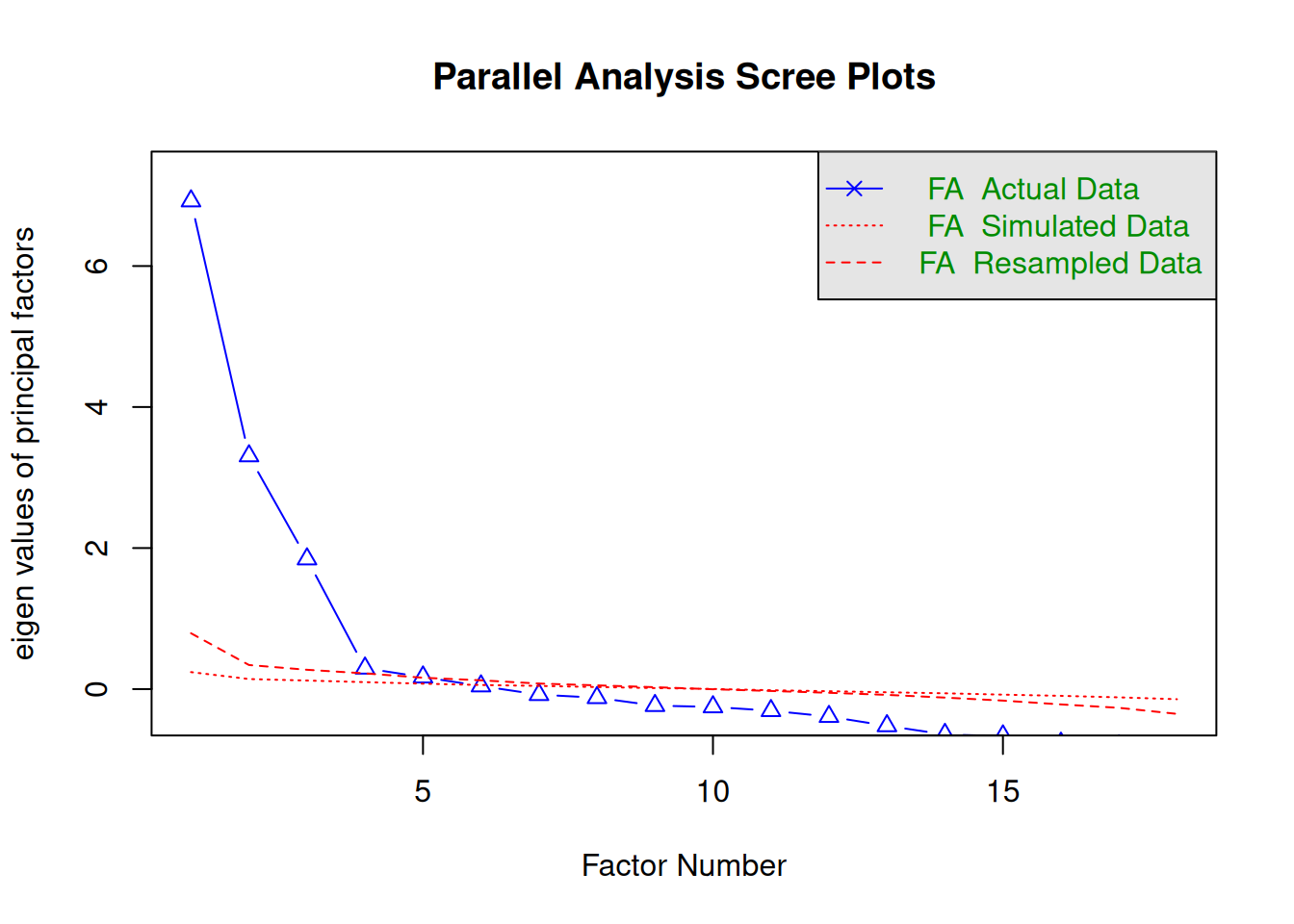
We generated the scree plot in Figure 22.13 using the psych::fa.parallel() function of the psych package (Revelle, 2025). The optimal coordinates and the acceleration factor attempt to operationalize the Cattell scree test: i.e., the “elbow” of the scree plot (Ruscio & Roche, 2012). The optimal coordinators factor is quantified using a series of linear equations to determine whether observed eigenvalues exceed the predicted values. The acceleration factor is quantified using the acceleration of the curve, that is, the second derivative. The Kaiser-Guttman rule states to keep principal components whose eigenvalues are greater than 1. However, for exploratory factor analysis (as opposed to PCA), the criterion is to keep the factors whose eigenvalues are greater than zero (i.e., not the factors whose eigenvalues are greater than 1) (Dinno, 2014).
The number of factors to keep would depend on which criteria one uses. Based on the rule to keep factors whose eigenvalues are greater than zero and based on the parallel test, we would keep five factors. However, based on the Cattell scree test (the “elbow” of the screen plot minus one), we would keep three factors. If using the optimal coordinates, we would keep eight factors; if using the acceleration factor, we would keep one factor. Therefore, interpretability of the factors would be important for deciding how many factors to keep.
Code
Parallel analysis suggests that the number of factors = 5 and the number of components = NA 
We generated the scree plot in Figure 22.14 using the nFactors::nScree() and nFactors::plotnScree() functions of the nFactors package (Raiche & Magis, 2025).
Code
#screeDataEFA <- nFactors::nScree(
# x = cor( # throws error with correlation matrix, so use covariance instead (below)
# dataForFA[faVars],
# use = "pairwise.complete.obs"),
# model = "factors")
screeDataEFA <- nFactors::nScree(
x = cov(
dataForFA[faVars],
use = "pairwise.complete.obs"),
cor = FALSE,
model = "factors")
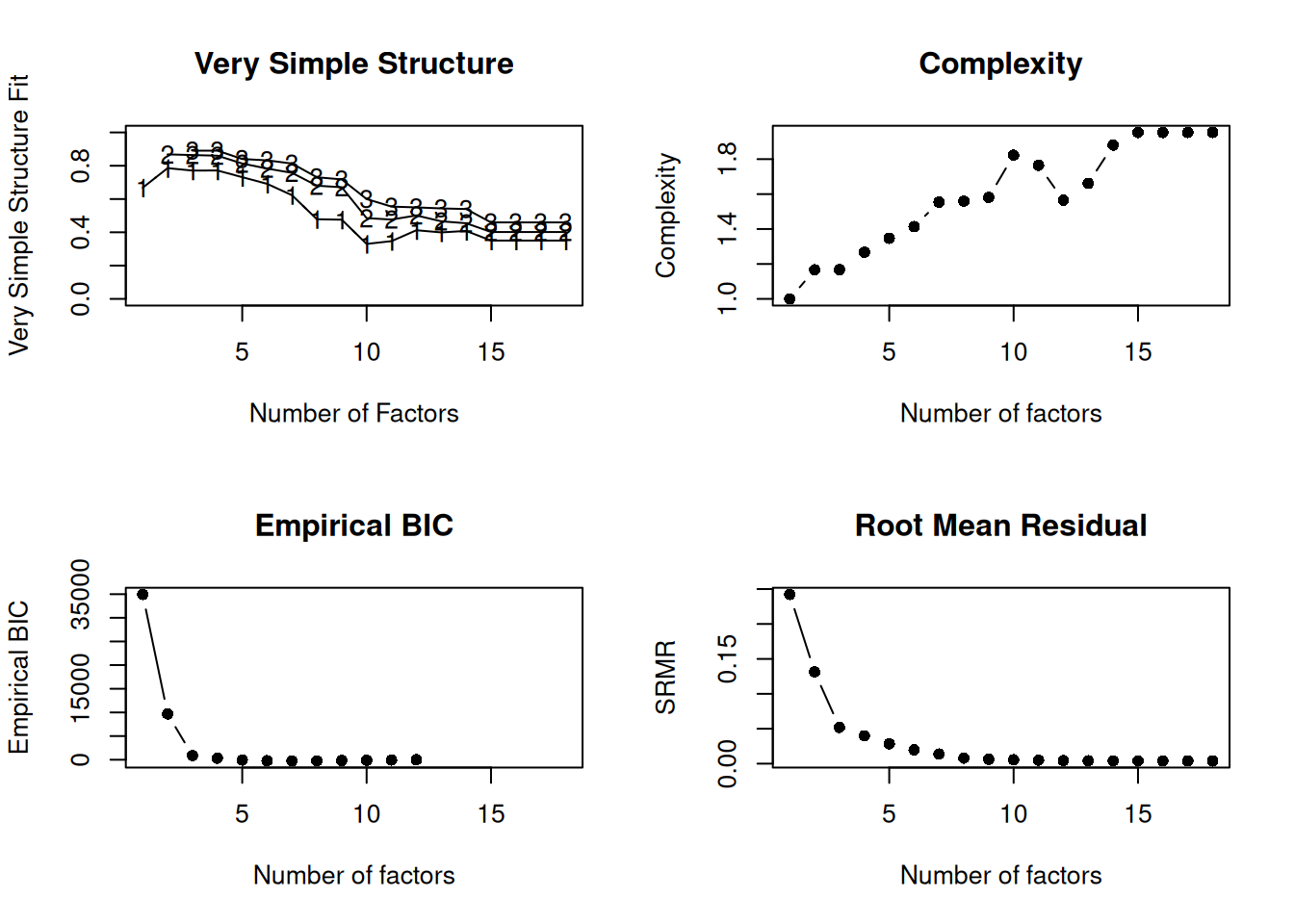
nFactors::plotnScree(screeDataEFA)
We generated the very simple structure (VSS) plots in Figures 22.15 and 22.16 using the psych::vss() and psych::nfactors() functions of the psych package (Revelle, 2025). In addition to VSS plots, the output also provides additional criteria by which to determine the optimal number of factors, each for which lower values are better, including the Velicer minimum average partial (MAP) test, the Bayesian information criterion (BIC), the sample size-adjusted BIC (SABIC), and the root mean square error of approximation (RMSEA). Depending on the criterion, the optimal number of factors extracted varies between 2 and 8 factors.
Very Simple Structure
Call: psych::vss(x = dataForFA[faVars], rotate = "oblimin", fm = "minres")
VSS complexity 1 achieves a maximimum of 0.79 with 2 factors
VSS complexity 2 achieves a maximimum of 0.87 with 2 factors
The Velicer MAP achieves a minimum of 0.13 with 3 factors
BIC achieves a minimum of 121337.1 with 8 factors
Sample Size adjusted BIC achieves a minimum of 121454.6 with 8 factors
Statistics by number of factors
vss1 vss2 map dof chisq prob sqresid fit RMSEA BIC SABIC complex
1 0.67 0.00 0.19 135 150953 0 26.4 0.67 0.75 149927 150356 1.0
2 0.79 0.87 0.16 118 137866 0 10.5 0.87 0.76 136969 137344 1.2
3 0.77 0.86 0.13 102 NaN NaN 8.6 0.89 NA NA NA 1.2
4 0.77 0.86 0.14 87 132838 0 8.0 0.90 0.87 132176 132453 1.3
5 0.73 0.81 0.30 73 150832 0 10.0 0.87 1.02 150277 150509 1.3
6 0.69 0.79 0.45 60 NaN NaN 11.6 0.85 NA NA NA 1.4
7 0.62 0.76 1.28 48 NaN NaN 13.1 0.84 NA NA NA 1.6
8 0.48 0.68 NaN 37 121618 0 17.6 0.78 1.28 121337 121455 1.6
eChisq SRMR eCRMS eBIC
1 35900 0.242 0.258 34874
2 10587 0.132 0.150 9690
3 1660 0.052 0.064 885
4 978 0.040 0.053 317
5 495 0.028 0.041 -60
6 240 0.020 0.032 -216
7 116 0.014 0.025 -248
8 39 0.008 0.016 -242
Code
Number of factors
Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm,
n.obs = n.obs, plot = FALSE, title = title, use = use, cor = cor)
VSS complexity 1 achieves a maximimum of 0.79 with 2 factors
VSS complexity 2 achieves a maximimum of 0.87 with 2 factors
The Velicer MAP achieves a minimum of 0.13 with 3 factors
Empirical BIC achieves a minimum of -248.29 with 7 factors
Sample Size adjusted BIC achieves a minimum of 107165.5 with 9 factors
Statistics by number of factors
vss1 vss2 map dof chisq prob sqresid fit RMSEA BIC SABIC complex
1 0.67 0.00 0.19 135 150953 0 26.4 0.67 0.75 149927 150356 1.0
2 0.79 0.87 0.16 118 137866 0 10.5 0.87 0.76 136969 137344 1.2
3 0.77 0.86 0.13 102 NaN NaN 8.6 0.89 NA NA NA 1.2
4 0.77 0.86 0.14 87 132838 0 8.0 0.90 0.87 132176 132453 1.3
5 0.73 0.81 0.30 73 150832 0 10.0 0.87 1.02 150277 150509 1.3
6 0.69 0.79 0.45 60 NaN NaN 11.6 0.85 NA NA NA 1.4
7 0.62 0.76 1.28 48 NaN NaN 13.1 0.84 NA NA NA 1.6
8 0.48 0.68 NaN 37 121618 0 17.6 0.78 1.28 121337 121455 1.6
9 0.48 0.67 NaN 27 107285 0 18.7 0.76 1.41 107080 107166 1.6
10 0.33 0.49 NaN 18 135089 0 27.9 0.65 1.94 134953 135010 1.8
11 0.32 0.46 NaN 10 NaN NaN 31.3 0.61 NA NA NA 1.8
12 0.37 0.46 NaN 3 NaN NaN 31.0 0.61 NA NA NA 1.6
13 0.42 0.48 NaN -3 NaN NA 29.7 0.63 NA NA NA 1.7
14 0.42 0.45 NaN -8 NaN NA 30.7 0.61 NA NA NA 1.9
15 0.25 0.33 NaN -12 NaN NA 40.2 0.49 NA NA NA 2.3
16 0.25 0.33 NaN -15 NaN NA 40.2 0.49 NA NA NA 2.3
17 0.25 0.33 NaN -17 NaN NA 40.2 0.49 NA NA NA 2.3
18 0.25 0.33 NA -18 NaN NA 40.2 0.49 NA NA NA 2.3
eChisq SRMR eCRMS eBIC
1 35900.3 0.2424 0.258 34874
2 10586.6 0.1316 0.150 9690
3 1660.4 0.0521 0.064 885
4 978.2 0.0400 0.053 317
5 495.2 0.0285 0.041 -60
6 239.8 0.0198 0.032 -216
7 116.5 0.0138 0.025 -248
8 39.3 0.0080 0.016 -242
9 25.3 0.0064 0.015 -180
10 18.8 0.0055 0.016 -118
11 14.7 0.0049 0.019 -61
12 12.3 0.0045 0.032 -11
13 10.3 0.0041 NA NA
14 9.9 0.0040 NA NA
15 9.8 0.0040 NA NA
16 9.8 0.0040 NA NA
17 9.8 0.0040 NA NA
18 9.8 0.0040 NA NA
We fit EFA models using the lavaan::efa() function of the lavaan package (Rosseel, 2012; Rosseel et al., 2024).
The model fits well according to CFI with 5 or more factors; the model fits well according to RMSEA with 6 or more factors. However, 5+ factors does not represent much of a simplification (relative to the 18 variables included). Moreover, in the model with four factors, only one variable had a significant loading on Factor 1. Thus, even with four factors, one of the factors does not seem to represent the aggregation of multiple variables. For these reasons, and because the “elbow test” for the scree plot suggested three factors, we decided to retain three factors and to see if we could achieve better fit by making additional model modifications (e.g., correlated residuals). Correlated residuals may be necessary, for example, when variables are correlated for reasons other than the latent factors.
This is lavaan 0.6-19 -- running exploratory factor analysis
Estimator ML
Rotation method GEOMIN OBLIQUE
Geomin epsilon 0.001
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 1997
Number of missing patterns 4
Overview models:
aic bic sabic chisq df pvalue cfi rmsea
nfactors = 1 124823.3 125125.6 124954.1 9257.081 135 0 0.222 0.568
nfactors = 2 117633.1 118030.6 117805.1 5228.488 118 0 0.666 0.402
nfactors = 3 113620.9 114108.0 113831.6 3182.380 102 0 0.731 0.398
nfactors = 4 110556.7 111127.8 110803.8 1451.176 87 0 0.898 0.283
nfactors = 5 109508.1 110157.6 109789.1 746.215 73 0 0.998 0.125
nfactors = 6 109268.7 109991.1 109581.2 502.433 60 0 1.000 0.044
nfactors = 7 108877.6 109667.1 109219.2 474.036 48 0 1.000 0.000
Eigenvalues correlation matrix:
ev1 ev2 ev3 ev4 ev5 ev6 ev7 ev8
6.62289 6.52671 2.96433 0.53788 0.40121 0.33897 0.21006 0.11017
ev9 ev10 ev11 ev12 ev13 ev14 ev15 ev16
0.08214 0.05588 0.04133 0.03158 0.02365 0.02080 0.01566 0.00891
ev17 ev18
0.00583 0.00201
Number of factors: 1
Standardized loadings: (* = significant at 1% level)
f1 unique.var communalities
completionsPerGame 0.987* 0.027 0.973
attemptsPerGame 0.974* 0.051 0.949
passing_yardsPerGame 0.994* 0.012 0.988
passing_tdsPerGame 0.864* 0.254 0.746
passing_air_yardsPerGame 0.692* 0.522 0.478
passing_yards_after_catchPerGame 0.771* 0.406 0.594
passing_first_downsPerGame 0.992* 0.016 0.984
avg_completed_air_yards .* 0.919 0.081
avg_intended_air_yards . 0.977 0.023
aggressiveness 0.997 0.003
max_completed_air_distance 0.472* 0.777 0.223
avg_air_distance 1.000 0.000
max_air_distance 0.367* 0.866 0.134
avg_air_yards_to_sticks .* 0.955 0.045
passing_cpoe .* 0.915 0.085
pass_comp_pct .* 0.914 0.086
passer_rating 0.627* 0.606 0.394
completion_percentage_above_expectation 0.519* 0.731 0.269
f1
Sum of squared loadings 7.057
Proportion of total 1.000
Proportion var 0.392
Cumulative var 0.392
Number of factors: 2
Standardized loadings: (* = significant at 1% level)
f1 f2 unique.var
completionsPerGame 0.986* 0.029
attemptsPerGame 0.974* * 0.050
passing_yardsPerGame 0.996* 0.008
passing_tdsPerGame 0.863* 0.255
passing_air_yardsPerGame 0.723* 0.695* 0.033
passing_yards_after_catchPerGame 0.748* -0.613* 0.029
passing_first_downsPerGame 0.990* 0.019
avg_completed_air_yards 0.965* 0.070
avg_intended_air_yards * 0.998* 0.002
aggressiveness . 0.785* 0.366
max_completed_air_distance .* 0.813* 0.288
avg_air_distance * 0.979* 0.032
max_air_distance .* 0.850* 0.260
avg_air_yards_to_sticks 0.991* 0.017
passing_cpoe 0.317* -0.345* 0.772
pass_comp_pct .* 0.917
passer_rating 0.614* . 0.614
completion_percentage_above_expectation 0.487* . 0.730
communalities
completionsPerGame 0.971
attemptsPerGame 0.950
passing_yardsPerGame 0.992
passing_tdsPerGame 0.745
passing_air_yardsPerGame 0.967
passing_yards_after_catchPerGame 0.971
passing_first_downsPerGame 0.981
avg_completed_air_yards 0.930
avg_intended_air_yards 0.998
aggressiveness 0.634
max_completed_air_distance 0.712
avg_air_distance 0.968
max_air_distance 0.740
avg_air_yards_to_sticks 0.983
passing_cpoe 0.228
pass_comp_pct 0.083
passer_rating 0.386
completion_percentage_above_expectation 0.270
f2 f1 total
Sum of sq (obliq) loadings 6.891 6.620 13.511
Proportion of total 0.510 0.490 1.000
Proportion var 0.383 0.368 0.751
Cumulative var 0.383 0.751 0.751
Factor correlations: (* = significant at 1% level)
f1 f2
f1 1.000
f2 -0.038 1.000
Number of factors: 3
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 unique.var
completionsPerGame 0.978* * 0.025
attemptsPerGame 0.993* * * 0.038
passing_yardsPerGame 0.987* * 0.010
passing_tdsPerGame 0.833* * .* 0.257
passing_air_yardsPerGame 0.791* 0.732* 0.022
passing_yards_after_catchPerGame 0.697* -0.603* 0.031
passing_first_downsPerGame 0.979* * 0.020
avg_completed_air_yards 0.784* 0.332* 0.043
avg_intended_air_yards 0.887* .* 0.002
aggressiveness 0.796* 0.349
max_completed_air_distance .* 0.662* 0.379* 0.181
avg_air_distance * 0.871* .* 0.024
max_air_distance .* 0.806* . 0.219
avg_air_yards_to_sticks 0.861* .* 0.012
passing_cpoe 1.001* 0.021
pass_comp_pct -0.474* 1.055* 0.107
passer_rating * 0.930* 0.090
completion_percentage_above_expectation 0.964* 0.046
communalities
completionsPerGame 0.975
attemptsPerGame 0.962
passing_yardsPerGame 0.990
passing_tdsPerGame 0.743
passing_air_yardsPerGame 0.978
passing_yards_after_catchPerGame 0.969
passing_first_downsPerGame 0.980
avg_completed_air_yards 0.957
avg_intended_air_yards 0.998
aggressiveness 0.651
max_completed_air_distance 0.819
avg_air_distance 0.976
max_air_distance 0.781
avg_air_yards_to_sticks 0.988
passing_cpoe 0.979
pass_comp_pct 0.893
passer_rating 0.910
completion_percentage_above_expectation 0.954
f2 f1 f3 total
Sum of sq (obliq) loadings 6.033 5.746 4.724 16.503
Proportion of total 0.366 0.348 0.286 1.000
Proportion var 0.335 0.319 0.262 0.917
Cumulative var 0.335 0.654 0.917 0.917
Factor correlations: (* = significant at 1% level)
f1 f2 f3
f1 1.000
f2 -0.145 1.000
f3 0.158 0.446 1.000
Number of factors: 4
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 f4
completionsPerGame 0.971* * *
attemptsPerGame * 1.025*
passing_yardsPerGame .* 0.901*
passing_tdsPerGame 0.381* 0.666*
passing_air_yardsPerGame 0.821* 0.733*
passing_yards_after_catchPerGame .* 0.598* -0.607*
passing_first_downsPerGame .* 0.904* *
avg_completed_air_yards .* 0.960*
avg_intended_air_yards 1.024*
aggressiveness 0.816*
max_completed_air_distance .* .* 0.777*
avg_air_distance 0.995*
max_air_distance .* 0.869*
avg_air_yards_to_sticks 1.003*
passing_cpoe .* 0.917*
pass_comp_pct -0.449* 1.065*
passer_rating .* 0.801*
completion_percentage_above_expectation .* 0.891*
unique.var communalities
completionsPerGame 0.015 0.985
attemptsPerGame 0.001 0.999
passing_yardsPerGame 0.001 0.999
passing_tdsPerGame 0.206 0.794
passing_air_yardsPerGame 0.015 0.985
passing_yards_after_catchPerGame 0.023 0.977
passing_first_downsPerGame 0.023 0.977
avg_completed_air_yards 0.067 0.933
avg_intended_air_yards 0.003 0.997
aggressiveness 0.322 0.678
max_completed_air_distance 0.293 0.707
avg_air_distance 0.034 0.966
max_air_distance 0.238 0.762
avg_air_yards_to_sticks 0.018 0.982
passing_cpoe 0.037 0.963
pass_comp_pct 0.074 0.926
passer_rating 0.148 0.852
completion_percentage_above_expectation 0.028 0.972
f3 f2 f4 f1 total
Sum of sq (obliq) loadings 6.953 5.369 3.406 0.726 16.454
Proportion of total 0.423 0.326 0.207 0.044 1.000
Proportion var 0.386 0.298 0.189 0.040 0.914
Cumulative var 0.386 0.685 0.874 0.914 0.914
Factor correlations: (* = significant at 1% level)
f1 f2 f3 f4
f1 1.000
f2 0.391 1.000
f3 -0.006 -0.171 1.000
f4 0.279 0.130 0.433 1.000
Number of factors: 5
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 f4 f5
completionsPerGame 0.952* * * .*
attemptsPerGame 0.979* *
passing_yardsPerGame 0.864* .* * *
passing_tdsPerGame 0.646* 0.439* * *
passing_air_yardsPerGame 0.801* * 0.760* *
passing_yards_after_catchPerGame 0.527* 0.301* -0.611* .* *
passing_first_downsPerGame 0.878* .* *
avg_completed_air_yards * 1.007* .* .*
avg_intended_air_yards 1.005* *
aggressiveness .* 0.792*
max_completed_air_distance .* .* 0.734*
avg_air_distance * 0.943* .*
max_air_distance .* 0.662* .* .*
avg_air_yards_to_sticks 0.974* *
passing_cpoe .* * 0.899*
pass_comp_pct -0.302* 1.038*
passer_rating 0.320* * 0.758*
completion_percentage_above_expectation .* 0.851*
unique.var communalities
completionsPerGame 0.008 0.992
attemptsPerGame 0.005 0.995
passing_yardsPerGame 0.003 0.997
passing_tdsPerGame 0.189 0.811
passing_air_yardsPerGame 0.016 0.984
passing_yards_after_catchPerGame 0.000 1.000
passing_first_downsPerGame 0.018 0.982
avg_completed_air_yards 0.037 0.963
avg_intended_air_yards 0.002 0.998
aggressiveness 0.432 0.568
max_completed_air_distance 0.343 0.657
avg_air_distance 0.048 0.952
max_air_distance 0.300 0.700
avg_air_yards_to_sticks 0.027 0.973
passing_cpoe 0.017 0.983
pass_comp_pct 0.100 0.900
passer_rating 0.136 0.864
completion_percentage_above_expectation 0.039 0.961
f3 f1 f5 f2 f4 total
Sum of sq (obliq) loadings 6.505 5.147 3.356 1.000 0.272 16.280
Proportion of total 0.400 0.316 0.206 0.061 0.017 1.000
Proportion var 0.361 0.286 0.186 0.056 0.015 0.904
Cumulative var 0.361 0.647 0.834 0.889 0.904 0.904
Factor correlations: (* = significant at 1% level)
f1 f2 f3 f4 f5
f1 1.000
f2 0.371 1.000
f3 -0.121 0.090 1.000
f4 0.189 0.090 0.020 1.000
f5 0.121 0.381 0.446 0.278 1.000
Number of factors: 6
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 f4 f5
completionsPerGame * 0.778* * .*
attemptsPerGame * 0.662* 0.433* .*
passing_yardsPerGame .* 0.651* * .* *
passing_tdsPerGame 0.434* 0.606*
passing_air_yardsPerGame 0.870* 0.631*
passing_yards_after_catchPerGame 0.313* .* 0.688* *
passing_first_downsPerGame .* 0.725* .*
avg_completed_air_yards .* * -0.571* 0.673*
avg_intended_air_yards 0.860* .*
aggressiveness .* 0.463* .*
max_completed_air_distance 0.675*
avg_air_distance 0.911* .*
max_air_distance 0.963* 0.483*
avg_air_yards_to_sticks 0.801* .*
passing_cpoe .* *
pass_comp_pct -0.303*
passer_rating .*
completion_percentage_above_expectation * .*
f6 unique.var communalities
completionsPerGame * 0.010 0.990
attemptsPerGame 0.000 1.000
passing_yardsPerGame 0.002 0.998
passing_tdsPerGame 0.199 0.801
passing_air_yardsPerGame .* 0.012 0.988
passing_yards_after_catchPerGame * 0.000 1.000
passing_first_downsPerGame * 0.019 0.981
avg_completed_air_yards * 0.000 1.000
avg_intended_air_yards 0.002 0.998
aggressiveness 0.445 0.555
max_completed_air_distance .* 0.340 0.660
avg_air_distance 0.048 0.952
max_air_distance . 0.291 0.709
avg_air_yards_to_sticks 0.027 0.973
passing_cpoe 0.908* 0.018 0.982
pass_comp_pct 1.013* 0.094 0.906
passer_rating 0.795* 0.146 0.854
completion_percentage_above_expectation 0.901* 0.038 0.962
f3 f2 f6 f4 f5 f1 total
Sum of sq (obliq) loadings 4.249 3.944 3.558 1.827 1.700 1.031 16.309
Proportion of total 0.261 0.242 0.218 0.112 0.104 0.063 1.000
Proportion var 0.236 0.219 0.198 0.102 0.094 0.057 0.906
Cumulative var 0.236 0.455 0.653 0.754 0.849 0.906 0.906
Factor correlations: (* = significant at 1% level)
f1 f2 f3 f4 f5 f6
f1 1.000
f2 0.443 1.000
f3 -0.158 -0.009 1.000
f4 0.429 0.642 -0.616 1.000
f5 0.100 0.369 0.818 -0.276 1.000
f6 0.324 0.259 0.472 -0.003 0.390 1.000
Number of factors: 7
Standardized loadings: (* = significant at 1% level)
f1 f2 f3 f4 f5
completionsPerGame 0.804* * 0.412* *
attemptsPerGame 0.759* * 0.462* *
passing_yardsPerGame 0.927* .* .* *
passing_tdsPerGame 0.954* * *
passing_air_yardsPerGame 0.477* 0.512* 0.370* .* *
passing_yards_after_catchPerGame 0.851* -0.430* *
passing_first_downsPerGame 0.931* .* * *
avg_completed_air_yards 0.533* 0.460*
avg_intended_air_yards 0.546* 0.513*
aggressiveness .* 0.720*
max_completed_air_distance 0.733*
avg_air_distance * 0.589* 0.453*
max_air_distance 0.682*
avg_air_yards_to_sticks * 0.452* 0.630*
passing_cpoe * *
pass_comp_pct -0.491*
passer_rating 0.354* .* *
completion_percentage_above_expectation *
f6 f7 unique.var
completionsPerGame .* 0.010
attemptsPerGame * 0.003
passing_yardsPerGame * 0.002
passing_tdsPerGame * 0.194
passing_air_yardsPerGame 0.008
passing_yards_after_catchPerGame * .* 0.000
passing_first_downsPerGame * * 0.017
avg_completed_air_yards 0.025
avg_intended_air_yards 0.001
aggressiveness 0.429
max_completed_air_distance 0.844* 0.000
avg_air_distance * 0.047
max_air_distance 0.445* 0.162
avg_air_yards_to_sticks 0.028
passing_cpoe 0.936* 0.019
pass_comp_pct 0.955* 0.041
passer_rating 0.728* 0.142
completion_percentage_above_expectation 0.973* 0.046
communalities
completionsPerGame 0.990
attemptsPerGame 0.997
passing_yardsPerGame 0.998
passing_tdsPerGame 0.806
passing_air_yardsPerGame 0.992
passing_yards_after_catchPerGame 1.000
passing_first_downsPerGame 0.983
avg_completed_air_yards 0.975
avg_intended_air_yards 0.999
aggressiveness 0.571
max_completed_air_distance 1.000
avg_air_distance 0.953
max_air_distance 0.838
avg_air_yards_to_sticks 0.972
passing_cpoe 0.981
pass_comp_pct 0.959
passer_rating 0.858
completion_percentage_above_expectation 0.954
f1 f7 f5 f2 f4 f3 f6 total
Sum of sq (obliq) loadings 5.204 3.416 2.537 2.471 1.308 1.043 0.846 16.826
Proportion of total 0.309 0.203 0.151 0.147 0.078 0.062 0.050 1.000
Proportion var 0.289 0.190 0.141 0.137 0.073 0.058 0.047 0.935
Cumulative var 0.289 0.479 0.620 0.757 0.830 0.888 0.935 0.935
Factor correlations: (* = significant at 1% level)
f1 f2 f3 f4 f5 f6 f7
f1 1.000
f2 0.009 1.000
f3 0.228 0.185 1.000
f4 -0.077 0.749 0.157 1.000
f5 -0.380 0.683 0.013 0.787 1.000
f6 0.385 0.155 -0.087 -0.198 -0.068 1.000
f7 0.204 0.611 -0.229 0.226 0.179 0.436 1.000A path diagram of the three-factor EFA model in Figure 22.17 was created using the lavaanPlot::lavaanPlot() function of the lavaanPlot package (Lishinski, 2024).
To make the plot interactive for editing, you can use the lavaangui::plot_lavaan() function of the lavaangui package (Karch, 2025b; Karch, 2025a):
Here is the syntax for estimating a three-factor EFA using exploratory structural equation modeling (ESEM). Estimating the model in a ESEM framework allows us to make modifications to the model, such as adding correlated residuals, and adding predictors or outcomes of the latent factors. The syntax below represents the same model (with the same fit indices) as the three-factor EFA model above.
Code
efa3factor_syntax <- '
# EFA Factor Loadings
efa("efa1")*f1 +
efa("efa1")*f2 +
efa("efa1")*f3 =~ completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame +
avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks + passing_cpoe + pass_comp_pct +
passer_rating + completion_percentage_above_expectation
'To fit the ESEM model, we use the lavaan::sem() function of the lavaan package (Rosseel, 2012; Rosseel et al., 2024).
The fit indices suggests that the model does not fit well to the data and that additional model modifications are necessary. The fit indices are below.
lavaan 0.6-19 ended normally after 1972 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 93
Row rank of the constraints matrix 30
Rotation method GEOMIN OBLIQUE
Geomin epsilon 0.001
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 1997
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 5446.238 3182.380
Degrees of freedom 102 102
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.711
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 23496.779
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.828
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.875 0.868
Tucker-Lewis Index (TLI) 0.813 0.802
Robust Comparative Fit Index (CFI) 0.731
Robust Tucker-Lewis Index (TLI) 0.597
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -56723.436 -56723.436
Scaling correction factor 1.784
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 1.745
for the MLR correction
Akaike (AIC) 113620.871 113620.871
Bayesian (BIC) 114108.019 114108.019
Sample-size adjusted Bayesian (SABIC) 113831.616 113831.616
Root Mean Square Error of Approximation:
RMSEA 0.162 0.123
90 Percent confidence interval - lower 0.158 0.120
90 Percent confidence interval - upper 0.166 0.126
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 1.000 1.000
Robust RMSEA 0.398
90 Percent confidence interval - lower 0.374
90 Percent confidence interval - upper 0.422
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.469 0.469
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 =~ efa1
completinsPrGm 7.843 0.092 84.934 0.000 7.843 0.978
attemptsPerGam 12.462 0.137 90.850 0.000 12.462 0.993
pssng_yrdsPrGm 91.612 1.051 87.181 0.000 91.612 0.987
passng_tdsPrGm 0.574 0.011 53.581 0.000 0.574 0.833
pssng_r_yrdsPG 95.681 1.913 50.010 0.000 95.681 0.791
pssng_yrds__PG 45.672 0.988 46.236 0.000 45.672 0.697
pssng_frst_dPG 4.445 0.053 84.193 0.000 4.445 0.979
avg_cmpltd_r_y 0.016 0.048 0.341 0.733 0.016 0.004
avg_ntndd_r_yr -0.043 0.043 -1.007 0.314 -0.043 -0.009
aggressiveness -0.289 0.381 -0.759 0.448 -0.289 -0.037
mx_cmpltd_r_ds 1.678 0.427 3.929 0.000 1.678 0.156
avg_air_distnc -0.212 0.075 -2.837 0.005 -0.212 -0.048
max_air_distnc 1.683 0.433 3.891 0.000 1.683 0.183
avg_r_yrds_t_s 0.005 0.042 0.130 0.897 0.005 0.001
passing_cpoe -0.486 0.224 -2.167 0.030 -0.486 -0.035
pass_comp_pct 0.000 0.001 0.674 0.500 0.000 0.003
passer_rating 2.776 0.956 2.905 0.004 2.776 0.085
cmpltn_prcnt__ -0.433 0.294 -1.476 0.140 -0.433 -0.036
f2 =~ efa1
completinsPrGm 0.024 0.030 0.789 0.430 0.024 0.003
attemptsPerGam 0.441 0.077 5.711 0.000 0.441 0.035
pssng_yrdsPrGm -0.299 0.289 -1.032 0.302 -0.299 -0.003
passng_tdsPrGm -0.032 0.009 -3.493 0.000 -0.032 -0.047
pssng_r_yrdsPG 88.473 1.714 51.627 0.000 88.473 0.732
pssng_yrds__PG -39.512 0.936 -42.207 0.000 -39.512 -0.603
pssng_frst_dPG -0.029 0.014 -2.084 0.037 -0.029 -0.006
avg_cmpltd_r_y 3.212 0.183 17.505 0.000 3.212 0.784
avg_ntndd_r_yr 4.141 0.192 21.602 0.000 4.141 0.887
aggressiveness 6.305 0.899 7.011 0.000 6.305 0.796
mx_cmpltd_r_ds 7.115 0.801 8.880 0.000 7.115 0.662
avg_air_distnc 3.836 0.213 18.021 0.000 3.836 0.871
max_air_distnc 7.399 0.747 9.907 0.000 7.399 0.806
avg_r_yrds_t_s 4.070 0.232 17.507 0.000 4.070 0.861
passing_cpoe -0.197 0.359 -0.549 0.583 -0.197 -0.014
pass_comp_pct -0.062 0.003 -19.422 0.000 -0.062 -0.474
passer_rating 0.515 0.711 0.725 0.469 0.515 0.016
cmpltn_prcnt__ 0.460 0.516 0.891 0.373 0.460 0.038
f3 =~ efa1
completinsPrGm 0.412 0.050 8.228 0.000 0.412 0.051
attemptsPerGam -0.681 0.079 -8.584 0.000 -0.681 -0.054
pssng_yrdsPrGm 4.081 0.458 8.908 0.000 4.081 0.044
passng_tdsPrGm 0.076 0.009 8.787 0.000 0.076 0.110
pssng_r_yrdsPG -2.190 1.615 -1.356 0.175 -2.190 -0.018
pssng_yrds__PG 0.357 0.473 0.754 0.451 0.357 0.005
pssng_frst_dPG 0.257 0.026 9.799 0.000 0.257 0.057
avg_cmpltd_r_y 1.359 0.216 6.299 0.000 1.359 0.332
avg_ntndd_r_yr 0.975 0.180 5.420 0.000 0.975 0.209
aggressiveness 0.088 0.585 0.151 0.880 0.088 0.011
mx_cmpltd_r_ds 4.079 0.945 4.317 0.000 4.079 0.379
avg_air_distnc 0.920 0.199 4.627 0.000 0.920 0.209
max_air_distnc 1.386 0.795 1.743 0.081 1.386 0.151
avg_r_yrds_t_s 1.148 0.208 5.513 0.000 1.148 0.243
passing_cpoe 13.717 0.570 24.081 0.000 13.717 1.001
pass_comp_pct 0.138 0.005 26.786 0.000 0.138 1.055
passer_rating 30.269 2.174 13.923 0.000 30.269 0.930
cmpltn_prcnt__ 11.669 0.674 17.315 0.000 11.669 0.964
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
f1 ~~
f2 -0.145 -0.145 -0.145
f3 0.158 0.158 0.158
f2 ~~
f3 0.446 NA 0.446 0.446
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.179 73.894 0.000 13.257 1.654
.attemptsPerGam 21.899 0.281 77.987 0.000 21.899 1.745
.pssng_yrdsPrGm 148.475 2.078 71.456 0.000 148.475 1.599
.passng_tdsPrGm 0.850 0.015 55.064 0.000 0.850 1.232
.pssng_r_yrdsPG 133.536 2.706 49.349 0.000 133.536 1.104
.pssng_yrds__PG 87.878 1.466 59.924 0.000 87.878 1.341
.pssng_frst_dPG 7.166 0.102 70.504 0.000 7.166 1.578
.avg_cmpltd_r_y 3.688 0.163 22.637 0.000 3.688 0.901
.avg_ntndd_r_yr 5.718 0.160 35.717 0.000 5.718 1.225
.aggressiveness 13.715 0.555 24.705 0.000 13.715 1.731
.mx_cmpltd_r_ds 33.432 0.628 53.242 0.000 33.432 3.109
.avg_air_distnc 19.136 0.170 112.818 0.000 19.136 4.344
.max_air_distnc 42.843 0.658 65.139 0.000 42.843 4.668
.avg_r_yrds_t_s -3.302 0.194 -17.052 0.000 -3.302 -0.699
.passing_cpoe -6.307 0.415 -15.184 0.000 -6.307 -0.460
.pass_comp_pct 0.591 0.003 191.608 0.000 0.591 4.523
.passer_rating 71.677 1.492 48.057 0.000 71.677 2.202
.cmpltn_prcnt__ -5.709 0.499 -11.453 0.000 -5.709 -0.472
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 1.618 0.117 13.850 0.000 1.618 0.025
.attemptsPerGam 6.034 0.385 15.676 0.000 6.034 0.038
.pssng_yrdsPrGm 87.431 8.326 10.501 0.000 87.431 0.010
.passng_tdsPrGm 0.122 0.006 20.582 0.000 0.122 0.257
.pssng_r_yrdsPG 327.643 29.177 11.230 0.000 327.643 0.022
.pssng_yrds__PG 132.016 8.865 14.892 0.000 132.016 0.031
.pssng_frst_dPG 0.413 0.026 15.885 0.000 0.413 0.020
.avg_cmpltd_r_y 0.717 0.074 9.648 0.000 0.717 0.043
.avg_ntndd_r_yr 0.033 0.014 2.432 0.015 0.033 0.002
.aggressiveness 21.887 NA 21.887 0.349
.mx_cmpltd_r_ds 20.925 NA 20.925 0.181
.avg_air_distnc 0.470 0.470 0.024
.max_air_distnc 18.462 NA 18.462 0.219
.avg_r_yrds_t_s 0.272 NA 0.272 0.012
.passing_cpoe 3.920 NA 3.920 0.021
.pass_comp_pct 0.002 0.002 0.107
.passer_rating 95.570 NA 95.570 0.090
.cmpltn_prcnt__ 6.744 NA 6.744 0.046
f1 1.000 1.000 1.000
f2 1.000 1.000 1.000
f3 1.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.975
attemptsPerGam 0.962
pssng_yrdsPrGm 0.990
passng_tdsPrGm 0.743
pssng_r_yrdsPG 0.978
pssng_yrds__PG 0.969
pssng_frst_dPG 0.980
avg_cmpltd_r_y 0.957
avg_ntndd_r_yr 0.998
aggressiveness 0.651
mx_cmpltd_r_ds 0.819
avg_air_distnc 0.976
max_air_distnc 0.781
avg_r_yrds_t_s 0.988
passing_cpoe 0.979
pass_comp_pct 0.893
passer_rating 0.910
cmpltn_prcnt__ 0.954Code
chisq df pvalue
5446.238 102.000 0.000
chisq.scaled df.scaled pvalue.scaled
3182.380 102.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.711 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.162 0.875
tli srmr rmsea.robust
0.813 0.469 0.398
cfi.robust tli.robust
0.731 0.597 $type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame 0.020 0.000
passing_yardsPerGame -0.004 -0.007 0.000
passing_tdsPerGame -0.022 -0.043 0.014 0.000
passing_air_yardsPerGame 0.003 0.007 0.001 -0.011
passing_yards_after_catchPerGame -0.006 0.001 0.006 0.001
passing_first_downsPerGame 0.000 -0.006 0.003 0.019
avg_completed_air_yards -0.103 -0.084 -0.056 -0.018
avg_intended_air_yards -0.083 -0.073 -0.052 -0.022
aggressiveness -0.044 -0.013 -0.031 -0.021
max_completed_air_distance 0.088 0.111 0.135 0.157
avg_air_distance -0.086 -0.072 -0.054 -0.025
max_air_distance 0.038 0.042 0.053 0.069
avg_air_yards_to_sticks -0.082 -0.070 -0.048 -0.010
passing_cpoe 0.022 0.022 0.027 0.024
pass_comp_pct 0.012 0.009 0.000 -0.016
passer_rating 0.070 0.065 0.105 0.184
completion_percentage_above_expectation 0.000 -0.003 0.000 -0.004
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame -0.008 0.000
passing_first_downsPerGame -0.003 -0.002 0.000
avg_completed_air_yards -0.071 -0.041 -0.066 0.000
avg_intended_air_yards -0.064 -0.010 -0.058 -0.017
aggressiveness -0.168 0.112 -0.021 -0.120
max_completed_air_distance -0.062 0.226 0.100 -0.185
avg_air_distance -0.085 0.010 -0.065 -0.038
max_air_distance -0.018 0.113 0.037 -0.133
avg_air_yards_to_sticks -0.072 0.003 -0.050 -0.024
passing_cpoe -0.026 0.061 0.025 -0.392
pass_comp_pct 0.003 0.000 0.001 -0.412
passer_rating -0.181 0.288 0.099 -0.601
completion_percentage_above_expectation -0.001 -0.001 0.001 -0.305
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness -0.129 0.000
max_completed_air_distance -0.238 -0.295 0.000
avg_air_distance -0.012 -0.134 -0.214 0.000
max_air_distance -0.090 -0.232 -0.010 -0.080 0.000
avg_air_yards_to_sticks -0.007 -0.122 -0.228 -0.019 -0.100
passing_cpoe -0.332 -0.421 -0.285 -0.345 -0.187
pass_comp_pct -0.341 -0.368 -0.237 -0.361 -0.148
passer_rating -0.582 -0.601 -0.370 -0.592 -0.371
completion_percentage_above_expectation -0.253 -0.298 -0.250 -0.266 -0.137
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe -0.350 0.000
pass_comp_pct -0.368 0.027 0.000
passer_rating -0.591 -0.085 0.079 0.000
completion_percentage_above_expectation -0.274 -0.003 -0.011 -0.132 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 0.423
avg_intended_air_yards aggressiveness
0.298 0.290
max_completed_air_distance avg_air_distance
0.441 0.310
max_air_distance avg_air_yards_to_sticks
0.155 0.361
passing_cpoe pass_comp_pct
0.039 -0.002
passer_rating completion_percentage_above_expectation
0.265 0.020 We can examine the model modification indices to identify parameters that, if estimated, would substantially improve model fit. For instance, the modification indices below indicate additional correlated residuals that could substantially improve model fit. However, it is generally not recommended to blindly estimate additional parameters solely based on modification indices, which can lead to data dredging and overfitting. Rather, it is generally advised to consider modification indices in light of theory. Based on the modification indices, we will add several correlated residuals to the model, to help account for why variables are associated with each other for reasons other than their underlying latent factors.
Below are factor scores from the model for the first six players:
f1 f2 f3
[1,] -0.09754741 -1.27792287 0.3402417
[2,] 0.22104543 -1.66217512 -0.9854985
[3,] 0.43811956 -1.83306001 -1.2122419
[4,] 0.06686317 0.08889638 0.7651668
[5,] 0.89608439 1.16088374 0.4625349
[6,] -0.02801652 0.13318370 -0.2137673A path diagram of the three-factor ESEM model is in Figure 22.18.
To make the plot interactive for editing, you can use the lavaangui::plot_lavaan() function of the lavaangui package (Karch, 2025b; Karch, 2025a):
Below is a modification of the three-factor model with correlated residuals. For instance, it makes sense that passing completions and attempts are related to each other (even after accounting for their latent factor).
Code
efa3factorModified_syntax <- '
# EFA Factor Loadings
efa("efa1")*F1 +
efa("efa1")*F2 +
efa("efa1")*F3 =~ completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame +
avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks + passing_cpoe + pass_comp_pct +
passer_rating + completion_percentage_above_expectation
# Correlated Residuals
completionsPerGame ~~ attemptsPerGame
passing_yardsPerGame ~~ passing_yards_after_catchPerGame
attemptsPerGame ~~ passing_yardsPerGame
attemptsPerGame ~~ passing_air_yardsPerGame
passing_air_yardsPerGame ~~ passing_yards_after_catchPerGame
passing_yards_after_catchPerGame ~~ avg_completed_air_yards
passing_tdsPerGame ~~ passer_rating
completionsPerGame ~~ passing_air_yardsPerGame
max_completed_air_distance ~~ max_air_distance
aggressiveness ~~ completion_percentage_above_expectation
'lavaan 0.6-19 ended normally after 370 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 103
Row rank of the constraints matrix 40
Rotation method GEOMIN OBLIQUE
Geomin epsilon 0.001
Rotation algorithm (rstarts) GPA (30)
Standardized metric TRUE
Row weights None
Number of observations 1997
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 1398.863 844.271
Degrees of freedom 92 92
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.657
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 23496.779
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.828
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.969 0.968
Tucker-Lewis Index (TLI) 0.949 0.946
Robust Comparative Fit Index (CFI) 0.948
Robust Tucker-Lewis Index (TLI) 0.913
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -54699.748 -54699.748
Scaling correction factor 1.828
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 1.745
for the MLR correction
Akaike (AIC) 109593.497 109593.497
Bayesian (BIC) 110136.639 110136.639
Sample-size adjusted Bayesian (SABIC) 109828.465 109828.465
Root Mean Square Error of Approximation:
RMSEA 0.084 0.064
90 Percent confidence interval - lower 0.080 0.061
90 Percent confidence interval - upper 0.088 0.067
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 0.967 0.000
Robust RMSEA 0.188
90 Percent confidence interval - lower 0.160
90 Percent confidence interval - upper 0.217
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.141 0.141
Parameter Estimates:
Standard errors Sandwich
Information bread Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~ efa1
completinsPrGm 7.797 0.093 83.643 0.000 7.797 0.972
attemptsPerGam 12.288 0.142 86.820 0.000 12.288 0.980
pssng_yrdsPrGm 91.931 1.029 89.340 0.000 91.931 0.990
passng_tdsPrGm 0.589 0.010 58.196 0.000 0.589 0.854
pssng_r_yrdsPG 89.910 1.782 50.446 0.000 89.910 0.744
pssng_yrds__PG 47.857 0.939 50.948 0.000 47.857 0.730
pssng_frst_dPG 4.468 0.052 86.490 0.000 4.468 0.984
avg_cmpltd_r_y 0.012 0.075 0.160 0.873 0.012 0.004
avg_ntndd_r_yr -0.059 0.070 -0.849 0.396 -0.059 -0.017
aggressiveness 0.017 0.185 0.094 0.925 0.017 0.003
mx_cmpltd_r_ds 1.694 0.463 3.661 0.000 1.694 0.200
avg_air_distnc -0.239 0.087 -2.753 0.006 -0.239 -0.073
max_air_distnc 1.460 0.427 3.420 0.001 1.460 0.197
avg_r_yrds_t_s 0.006 0.074 0.088 0.930 0.006 0.002
passing_cpoe -0.845 0.262 -3.232 0.001 -0.845 -0.058
pass_comp_pct 0.001 0.002 0.568 0.570 0.001 0.008
passer_rating 2.986 0.882 3.383 0.001 2.986 0.111
cmpltn_prcnt__ -0.693 0.324 -2.135 0.033 -0.693 -0.056
F2 =~ efa1
completinsPrGm -0.096 0.040 -2.401 0.016 -0.096 -0.012
attemptsPerGam 0.085 0.092 0.924 0.355 0.085 0.007
pssng_yrdsPrGm 0.880 0.327 2.692 0.007 0.880 0.009
passng_tdsPrGm -0.001 0.007 -0.199 0.842 -0.001 -0.002
pssng_r_yrdsPG 83.739 1.816 46.117 0.000 83.739 0.693
pssng_yrds__PG -36.815 0.947 -38.895 0.000 -36.815 -0.561
pssng_frst_dPG -0.000 0.016 -0.017 0.986 -0.000 -0.000
avg_cmpltd_r_y 2.950 0.129 22.781 0.000 2.950 0.954
avg_ntndd_r_yr 3.498 0.133 26.358 0.000 3.498 1.013
aggressiveness 5.141 0.728 7.062 0.000 5.141 0.791
mx_cmpltd_r_ds 5.949 0.654 9.103 0.000 5.949 0.702
avg_air_distnc 3.205 0.155 20.661 0.000 3.205 0.975
max_air_distnc 6.190 0.635 9.751 0.000 6.190 0.834
avg_r_yrds_t_s 3.413 0.173 19.747 0.000 3.413 0.986
passing_cpoe 0.921 0.594 1.551 0.121 0.921 0.063
pass_comp_pct -0.069 0.004 -17.051 0.000 -0.069 -0.531
passer_rating -0.462 0.385 -1.199 0.230 -0.462 -0.017
cmpltn_prcnt__ 0.971 0.529 1.835 0.067 0.971 0.078
F3 =~ efa1
completinsPrGm 0.430 0.088 4.864 0.000 0.430 0.054
attemptsPerGam -0.645 0.149 -4.344 0.000 -0.645 -0.051
pssng_yrdsPrGm 2.834 1.051 2.696 0.007 2.834 0.031
passng_tdsPrGm 0.053 0.011 5.014 0.000 0.053 0.077
pssng_r_yrdsPG 0.740 0.860 0.861 0.389 0.740 0.006
pssng_yrds__PG -1.842 1.405 -1.312 0.190 -1.842 -0.028
pssng_frst_dPG 0.201 0.054 3.751 0.000 0.201 0.044
avg_cmpltd_r_y 0.064 0.126 0.506 0.613 0.064 0.021
avg_ntndd_r_yr -0.116 0.067 -1.734 0.083 -0.116 -0.034
aggressiveness -2.492 0.704 -3.539 0.000 -2.492 -0.383
mx_cmpltd_r_ds 1.793 0.831 2.158 0.031 1.793 0.211
avg_air_distnc -0.051 0.091 -0.558 0.577 -0.051 -0.015
max_air_distnc -0.418 0.666 -0.627 0.531 -0.418 -0.056
avg_r_yrds_t_s 0.017 0.098 0.178 0.859 0.017 0.005
passing_cpoe 14.087 0.596 23.633 0.000 14.087 0.963
pass_comp_pct 0.142 0.005 27.409 0.000 0.142 1.090
passer_rating 24.552 1.832 13.399 0.000 24.552 0.910
cmpltn_prcnt__ 11.768 0.683 17.234 0.000 11.768 0.950
Covariances:
Estimate Std.Err z-value P(>|z|)
.completionsPerGame ~~
.attemptsPerGam 3.305 0.162 20.439 0.000
.passing_yardsPerGame ~~
.pssng_yrds__PG 92.975 7.878 11.801 0.000
.attemptsPerGame ~~
.pssng_yrdsPrGm 3.470 0.579 5.994 0.000
.pssng_r_yrdsPG 52.748 2.895 18.222 0.000
.passing_air_yardsPerGame ~~
.pssng_yrds__PG -231.835 11.670 -19.866 0.000
.passing_yards_after_catchPerGame ~~
.avg_cmpltd_r_y -6.025 0.424 -14.219 0.000
.passing_tdsPerGame ~~
.passer_rating 1.760 0.142 12.418 0.000
.completionsPerGame ~~
.pssng_r_yrdsPG 12.979 1.190 10.911 0.000
.max_completed_air_distance ~~
.max_air_distnc 9.119 0.882 10.341 0.000
.aggressiveness ~~
.cmpltn_prcnt__ 5.907 0.733 8.056 0.000
F1 ~~
F2 -0.096
F3 0.174
F2 ~~
F3 0.464
Std.lv Std.all
3.305 0.778
92.975 0.607
3.470 0.128
52.748 0.598
-231.835 -0.466
-6.025 -0.435
1.760 0.518
12.979 0.308
9.119 0.455
5.907 0.531
-0.096 -0.096
0.174 0.174
0.464 0.464
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.179 73.894 0.000 13.257 1.654
.attemptsPerGam 21.899 0.281 77.987 0.000 21.899 1.746
.pssng_yrdsPrGm 148.475 2.078 71.456 0.000 148.475 1.599
.passng_tdsPrGm 0.850 0.015 55.064 0.000 0.850 1.232
.pssng_r_yrdsPG 133.536 2.706 49.349 0.000 133.536 1.105
.pssng_yrds__PG 87.878 1.466 59.924 0.000 87.878 1.340
.pssng_frst_dPG 7.166 0.102 70.504 0.000 7.166 1.578
.avg_cmpltd_r_y 4.330 0.119 36.329 0.000 4.330 1.401
.avg_ntndd_r_yr 6.466 0.113 57.225 0.000 6.466 1.872
.aggressiveness 15.249 0.489 31.177 0.000 15.249 2.346
.mx_cmpltd_r_ds 34.809 0.512 68.017 0.000 34.809 4.105
.avg_air_distnc 19.834 0.122 163.126 0.000 19.834 6.033
.max_air_distnc 44.247 0.539 82.055 0.000 44.247 5.965
.avg_r_yrds_t_s -2.545 0.142 -17.947 0.000 -2.545 -0.735
.passing_cpoe -7.195 0.494 -14.570 0.000 -7.195 -0.492
.pass_comp_pct 0.591 0.003 189.418 0.000 0.591 4.527
.passer_rating 74.014 1.181 62.674 0.000 74.014 2.743
.cmpltn_prcnt__ -6.332 0.470 -13.465 0.000 -6.332 -0.511
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 2.029 0.103 19.769 0.000 2.029 0.032
.attemptsPerGam 8.890 0.348 25.558 0.000 8.890 0.057
.pssng_yrdsPrGm 83.182 8.537 9.744 0.000 83.182 0.010
.passng_tdsPrGm 0.115 0.006 19.546 0.000 0.115 0.241
.pssng_r_yrdsPG 876.335 5.872 149.236 0.000 876.335 0.060
.pssng_yrds__PG 281.884 11.072 25.459 0.000 281.884 0.066
.pssng_frst_dPG 0.318 0.027 11.879 0.000 0.318 0.015
.avg_cmpltd_r_y 0.680 0.063 10.844 0.000 0.680 0.071
.avg_ntndd_r_yr 0.005 0.014 0.370 0.712 0.005 0.000
.aggressiveness 21.544 21.544 0.510
.mx_cmpltd_r_ds 21.394 21.394 0.298
.avg_air_distnc 0.480 0.480 0.044
.max_air_distnc 18.762 18.762 0.341
.avg_r_yrds_t_s 0.286 0.286 0.024
.passing_cpoe 6.089 6.089 0.028
.pass_comp_pct 0.001 0.000 1431.338 0.000 0.001 0.064
.passer_rating 100.731 100.731 0.138
.cmpltn_prcnt__ 5.735 5.735 0.037
F1 1.000 1.000 1.000
F2 1.000 1.000 1.000
F3 1.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.968
attemptsPerGam 0.943
pssng_yrdsPrGm 0.990
passng_tdsPrGm 0.759
pssng_r_yrdsPG 0.940
pssng_yrds__PG 0.934
pssng_frst_dPG 0.985
avg_cmpltd_r_y 0.929
avg_ntndd_r_yr 1.000
aggressiveness 0.490
mx_cmpltd_r_ds 0.702
avg_air_distnc 0.956
max_air_distnc 0.659
avg_r_yrds_t_s 0.976
passing_cpoe 0.972
pass_comp_pct 0.936
passer_rating 0.862
cmpltn_prcnt__ 0.963The model fits substantially better (though not perfectly) with the additional correlated residuals. Below are the model fit indices:
Code
chisq df pvalue
1398.863 92.000 0.000
chisq.scaled df.scaled pvalue.scaled
844.271 92.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.657 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.084 0.969
tli srmr rmsea.robust
0.949 0.141 0.188
cfi.robust tli.robust
0.948 0.913 $type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame 0.000 0.000
passing_yardsPerGame -0.001 -0.001 0.000
passing_tdsPerGame -0.030 -0.047 0.004 0.000
passing_air_yardsPerGame 0.004 0.003 -0.001 -0.036
passing_yards_after_catchPerGame -0.004 -0.002 0.001 0.017
passing_first_downsPerGame 0.001 0.000 0.000 0.007
avg_completed_air_yards -0.052 -0.045 -0.025 0.004
avg_intended_air_yards -0.046 -0.041 -0.035 -0.017
aggressiveness -0.025 -0.021 -0.032 -0.022
max_completed_air_distance 0.059 0.079 0.090 0.110
avg_air_distance -0.037 -0.029 -0.025 -0.010
max_air_distance 0.043 0.042 0.039 0.047
avg_air_yards_to_sticks -0.053 -0.047 -0.040 -0.012
passing_cpoe 0.050 0.054 0.055 0.053
pass_comp_pct 0.002 0.000 0.001 -0.002
passer_rating 0.038 0.037 0.072 0.064
completion_percentage_above_expectation 0.016 0.019 0.016 0.013
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame 0.001 0.000
passing_first_downsPerGame -0.002 0.003 0.000
avg_completed_air_yards -0.054 0.006 -0.027 0.000
avg_intended_air_yards -0.045 -0.011 -0.033 -0.009
aggressiveness -0.024 -0.031 -0.013 0.048
max_completed_air_distance -0.058 0.157 0.061 -0.076
avg_air_distance -0.049 0.011 -0.028 -0.020
max_air_distance 0.035 0.044 0.029 -0.050
avg_air_yards_to_sticks -0.061 -0.003 -0.033 -0.007
passing_cpoe -0.065 0.131 0.055 -0.233
pass_comp_pct 0.002 0.000 0.000 -0.127
passer_rating -0.190 0.251 0.069 -0.353
completion_percentage_above_expectation -0.029 0.044 0.019 -0.131
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness 0.039 0.000
max_completed_air_distance -0.144 -0.047 0.000
avg_air_distance -0.002 0.043 -0.110 0.000
max_air_distance -0.012 -0.039 -0.028 0.010 0.000
avg_air_yards_to_sticks -0.002 0.056 -0.134 -0.002 -0.019
passing_cpoe -0.225 -0.097 -0.191 -0.243 -0.057
pass_comp_pct -0.111 -0.026 -0.092 -0.142 0.040
passer_rating -0.378 -0.225 -0.223 -0.391 -0.179
completion_percentage_above_expectation -0.127 -0.028 -0.144 -0.145 0.010
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe -0.246 0.000
pass_comp_pct -0.145 0.067 0.000
passer_rating -0.394 -0.044 0.088 0.000
completion_percentage_above_expectation -0.151 -0.004 0.008 -0.099 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 0.182
avg_intended_air_yards aggressiveness
0.078 0.059
max_completed_air_distance avg_air_distance
0.242 0.093
max_air_distance avg_air_yards_to_sticks
-0.032 0.129
passing_cpoe pass_comp_pct
0.106 -0.001
passer_rating completion_percentage_above_expectation
0.174 0.073 Below are factor scores from the model for the first six players:
Code
F1 F2 F3
[1,] -0.04015747 -0.92275825 0.3926962
[2,] 0.18405090 -1.63622767 -1.0333355
[3,] 0.42256884 -2.26494492 -1.5053879
[4,] 0.15119168 0.28877489 0.7973461
[5,] 0.83159338 1.09556751 0.4306327
[6,] -0.13577151 0.08173552 -0.1962239The path diagram of the modified ESEM model with correlated residuals is in Figure 22.19.
Model fit of nested models can be compared with a chi-square difference test. This allows us to evaluate whether the more complex model fits signficantly better than the less complex model. In this case, our more complex model is the three-factor model with correlated residuals; the less complex model is the three-factor model without correlated residuals. The modified model with the correlated residuals and the original model are considered “nested” models. The original model is nested within the modified model because the modified model includes all of the terms of the original model along with additional terms.
In this case, the model with the correlated residuals fit significantly better (i.e., has a significantly smaller chi-square value) than the model without the correlated residuals.
Here are the variables that had a standardized loading greater than 0.3 on each of the factors:
Code
factor1vars <- c(
"completionsPerGame","attemptsPerGame","passing_yardsPerGame","passing_tdsPerGame",
"passing_air_yardsPerGame","passing_yards_after_catchPerGame","passing_first_downsPerGame")
factor2vars <- c(
"avg_completed_air_yards","avg_intended_air_yards","aggressiveness","max_completed_air_distance",
"avg_air_distance","max_air_distance","avg_air_yards_to_sticks")
factor3vars <- c(
"passing_cpoe","pass_comp_pct","passer_rating","completion_percentage_above_expectation")The variables that loaded most strongly onto factor 1 appear to reflect Quarterback usage: completions per game, passing attempts per game, passing yards per game, passing touchdowns per game, passing air yards (total horizontal distance the ball travels on all pass attempts) per game, passing yards after the catch per game, and first downs gained per game by passing. Quarterbacks who tend to throw more tend to have higher levels on those variables. Thus, we label component 1 as “Usage”, which reflects total Quarterback involvement, regardless of efficiency or outcome.
The variables that loaded most strongly onto factor 2 appear to reflect Quarterback aggressiveness: average air yards on completed passes, average air yards on all attempted passes, aggressiveness (percentage of passing attempts thrown into tight windows, where there is a defender within one yard or less of the receiver at the time of the completion or incompletion), average amount of air yards ahead of or behind the first down marker on passing attempts, average air distance (the true three-dimensional distance the ball travels in the air), maximum air distance, and maximum air distance on completed passes. Quarterbacks who throw the ball farther and into tighter windows tend to have higher values on those variables. Thus, we label component 2 as “Aggressiveness”, which reflects throwing longer, more difficult passes with a tight window.
The variables that loaded most strongly onto factor 3 appear to reflect Quarterback performance: passing completion percentage above expectation, pass completion percentage, and passer rating. Quarterbacks who perform better tend to have higher values on those variables. Thus, we label component 3 as “Performance”.
Here are the players and seasons that showed the highest levels of Quarterback “Usage”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Usage”:
Code
Here are the players and seasons that showed the highest levels of Quarterback “Aggressiveness”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Aggressiveness”:
Code
Here are the players and seasons that showed the highest levels of Quarterback “Performance”:
Code
If we restrict it to Quarterbacks who played at least 10 games in the season, here are the players and seasons that showed the highest levels of Quarterback “Performance”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Performance”:
Code
If we restrict it to Quarterbacks who played at least 10 games in the season, here are the players and seasons that showed the lowest levels of Quarterback “Performance”:
22.7 Example of Confirmatory Factor Analysis
We fit CFA models using the lavaan::cfa() function of the lavaan package (Rosseel, 2012; Rosseel et al., 2024). We compare one-, two-, and three-factor CFA models.
Below is the syntax for the one-factor CFA model:
Code
cfa1factor_syntax <- '
#Factor loadings
F1 =~ completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame +
avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks + passing_cpoe + pass_comp_pct +
passer_rating + completion_percentage_above_expectation
'lavaan 0.6-19 ended normally after 200 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 54
Row rank of the constraints matrix 36
Number of observations 1997
Number of clusters [player_id] 397
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 16714.647 8844.907
Degrees of freedom 135 135
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.890
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 22341.153
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.922
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.613 0.607
Tucker-Lewis Index (TLI) 0.561 0.555
Robust Comparative Fit Index (CFI) 0.222
Robust Tucker-Lewis Index (TLI) 0.119
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -62357.640 -62357.640
Scaling correction factor 2.558
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 2.081
for the MLR correction
Akaike (AIC) 124823.280 124823.280
Bayesian (BIC) 125125.648 125125.648
Sample-size adjusted Bayesian (SABIC) 124954.087 124954.087
Root Mean Square Error of Approximation:
RMSEA 0.248 0.180
90 Percent confidence interval - lower 0.245 0.177
90 Percent confidence interval - upper 0.251 0.182
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 1.000 1.000
Robust RMSEA 0.568
90 Percent confidence interval - lower 0.550
90 Percent confidence interval - upper 0.585
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.378 0.378
Parameter Estimates:
Standard errors Robust.cluster
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~
completinsPrGm 7.910 0.123 64.369 0.000 7.910 0.987
attemptsPerGam 12.223 0.170 71.817 0.000 12.223 0.974
pssng_yrdsPrGm 92.316 1.484 62.197 0.000 92.316 0.994
passng_tdsPrGm 0.596 0.019 31.441 0.000 0.596 0.864
pssng_r_yrdsPG 83.627 3.622 23.090 0.000 83.627 0.692
pssng_yrds__PG 50.523 1.525 33.131 0.000 50.523 0.771
pssng_frst_dPG 4.505 0.079 56.960 0.000 4.505 0.992
avg_cmpltd_r_y 0.410 0.105 3.913 0.000 0.410 0.284
avg_ntndd_r_yr 0.212 0.107 1.977 0.048 0.212 0.152
aggressiveness -0.274 0.477 -0.574 0.566 -0.274 -0.053
mx_cmpltd_r_ds 2.798 0.423 6.618 0.000 2.798 0.472
avg_air_distnc 0.029 0.115 0.250 0.803 0.029 0.020
max_air_distnc 1.952 0.435 4.489 0.000 1.952 0.367
avg_r_yrds_t_s 0.316 0.114 2.784 0.005 0.316 0.213
passing_cpoe 3.463 0.520 6.657 0.000 3.463 0.292
pass_comp_pct 0.039 0.005 7.468 0.000 0.039 0.294
passer_rating 11.654 1.169 9.972 0.000 11.654 0.627
cmpltn_prcnt__ 2.980 0.412 7.241 0.000 2.980 0.519
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.391 33.868 0.000 13.257 1.654
.attemptsPerGam 21.899 0.581 37.714 0.000 21.899 1.745
.pssng_yrdsPrGm 148.475 4.622 32.121 0.000 148.475 1.599
.passng_tdsPrGm 0.850 0.036 23.842 0.000 0.850 1.232
.pssng_r_yrdsPG 133.536 5.766 23.158 0.000 133.536 1.104
.pssng_yrds__PG 87.878 2.982 29.472 0.000 87.878 1.341
.pssng_frst_dPG 7.166 0.228 31.455 0.000 7.166 1.578
.avg_cmpltd_r_y 5.555 0.100 55.687 0.000 5.555 3.851
.avg_ntndd_r_yr 7.934 0.107 74.362 0.000 7.934 5.669
.aggressiveness 16.707 0.418 39.977 0.000 16.707 3.249
.mx_cmpltd_r_ds 37.862 0.434 87.240 0.000 37.862 6.387
.avg_air_distnc 21.196 0.108 196.598 0.000 21.196 14.668
.max_air_distnc 46.728 0.425 109.894 0.000 46.728 8.775
.avg_r_yrds_t_s -1.077 0.113 -9.561 0.000 -1.077 -0.726
.passing_cpoe -2.755 0.429 -6.419 0.000 -2.755 -0.232
.pass_comp_pct 0.589 0.004 142.846 0.000 0.589 4.473
.passer_rating 79.852 1.208 66.096 0.000 79.852 4.300
.cmpltn_prcnt__ -2.411 0.411 -5.868 0.000 -2.411 -0.420
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 1.707 0.123 13.838 0.000 1.707 0.027
.attemptsPerGam 8.050 0.457 17.633 0.000 8.050 0.051
.pssng_yrdsPrGm 99.776 9.145 10.911 0.000 99.776 0.012
.passng_tdsPrGm 0.121 0.007 17.385 0.000 0.121 0.254
.pssng_r_yrdsPG 7628.828 517.086 14.753 0.000 7628.828 0.522
.pssng_yrds__PG 1742.218 130.951 13.304 0.000 1742.218 0.406
.pssng_frst_dPG 0.336 0.025 13.212 0.000 0.336 0.016
.avg_cmpltd_r_y 1.914 0.157 12.167 0.000 1.914 0.919
.avg_ntndd_r_yr 1.914 0.170 11.281 0.000 1.914 0.977
.aggressiveness 26.371 3.308 7.973 0.000 26.371 0.997
.mx_cmpltd_r_ds 27.315 2.789 9.793 0.000 27.315 0.777
.avg_air_distnc 2.087 0.175 11.912 0.000 2.087 1.000
.max_air_distnc 24.547 2.486 9.876 0.000 24.547 0.866
.avg_r_yrds_t_s 2.102 0.210 10.026 0.000 2.102 0.955
.passing_cpoe 128.838 13.709 9.398 0.000 128.838 0.915
.pass_comp_pct 0.016 0.001 11.749 0.000 0.016 0.914
.passer_rating 209.102 20.025 10.442 0.000 209.102 0.606
.cmpltn_prcnt__ 24.102 2.730 8.830 0.000 24.102 0.731
F1 1.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.973
attemptsPerGam 0.949
pssng_yrdsPrGm 0.988
passng_tdsPrGm 0.746
pssng_r_yrdsPG 0.478
pssng_yrds__PG 0.594
pssng_frst_dPG 0.984
avg_cmpltd_r_y 0.081
avg_ntndd_r_yr 0.023
aggressiveness 0.003
mx_cmpltd_r_ds 0.223
avg_air_distnc 0.000
max_air_distnc 0.134
avg_r_yrds_t_s 0.045
passing_cpoe 0.085
pass_comp_pct 0.086
passer_rating 0.394
cmpltn_prcnt__ 0.269The one-factor model did not fit well according to the fit indices:
Code
chisq df pvalue
16714.647 135.000 0.000
chisq.scaled df.scaled pvalue.scaled
8844.907 135.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.890 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.248 0.613
tli srmr rmsea.robust
0.561 0.378 0.568
cfi.robust tli.robust
0.222 0.119 $type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame 0.023 0.000
passing_yardsPerGame -0.003 -0.003 0.000
passing_tdsPerGame -0.026 -0.050 0.011 0.000
passing_air_yardsPerGame 0.012 0.009 0.003 -0.021
passing_yards_after_catchPerGame -0.008 0.014 0.009 0.005
passing_first_downsPerGame -0.001 -0.006 0.001 0.014
avg_completed_air_yards -0.401 -0.422 -0.368 -0.280
avg_intended_air_yards -0.302 -0.323 -0.283 -0.220
aggressiveness -0.117 -0.102 -0.113 -0.098
max_completed_air_distance -0.222 -0.239 -0.188 -0.112
avg_air_distance -0.210 -0.230 -0.190 -0.141
max_air_distance -0.205 -0.224 -0.201 -0.153
avg_air_yards_to_sticks -0.340 -0.362 -0.320 -0.241
passing_cpoe -0.091 -0.176 -0.098 -0.037
pass_comp_pct -0.001 -0.087 -0.020 0.021
passer_rating -0.274 -0.354 -0.252 -0.082
completion_percentage_above_expectation -0.351 -0.434 -0.364 -0.275
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame -0.430 0.000
passing_first_downsPerGame 0.000 -0.003 0.000
avg_completed_air_yards 0.357 -0.858 -0.371 0.000
avg_intended_air_yards 0.456 -0.789 -0.283 0.910
aggressiveness 0.333 -0.436 -0.099 0.647
max_completed_air_distance 0.286 -0.537 -0.216 0.547
avg_air_distance 0.489 -0.687 -0.196 0.913
max_air_distance 0.410 -0.614 -0.213 0.607
avg_air_yards_to_sticks 0.411 -0.802 -0.315 0.884
passing_cpoe 0.173 -0.335 -0.089 0.197
pass_comp_pct -0.030 -0.054 -0.010 -0.217
passer_rating -0.144 -0.282 -0.247 -0.135
completion_percentage_above_expectation 0.057 -0.604 -0.353 0.243
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness 0.671 0.000
max_completed_air_distance 0.553 0.377 0.000
avg_air_distance 0.971 0.651 0.621 0.000
max_air_distance 0.718 0.465 0.596 0.758 0.000
avg_air_yards_to_sticks 0.953 0.671 0.538 0.957 0.683
passing_cpoe 0.218 -0.051 0.262 0.231 0.231
pass_comp_pct -0.214 -0.354 -0.021 -0.205 -0.088
passer_rating -0.109 -0.232 0.007 -0.053 -0.078
completion_percentage_above_expectation 0.291 0.114 0.206 0.334 0.222
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe 0.205 0.000
pass_comp_pct -0.229 0.778 0.000
passer_rating -0.133 0.669 0.700 0.000
completion_percentage_above_expectation 0.261 0.811 0.641 0.466 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 -0.279
avg_intended_air_yards aggressiveness
-0.352 -0.161
max_completed_air_distance avg_air_distance
-0.200 -0.331
max_air_distance avg_air_yards_to_sticks
-0.363 -0.322
passing_cpoe pass_comp_pct
-0.228 0.013
passer_rating completion_percentage_above_expectation
-0.054 -0.262 Below are factor scores from the model for the first six players:
F1
[1,] -0.07070045
[2,] 0.15971691
[3,] 0.41749827
[4,] 0.11237086
[5,] 0.88378483
[6,] -0.07485071The path diagram of the one-factor CFA model is in Figure 22.20.
Below is the syntax for the two-factor CFA model:
Code
cfa2factor_syntax <- '
#Factor loadings
F1 =~ completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame
F2 =~ avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks + passing_cpoe + pass_comp_pct +
passer_rating + completion_percentage_above_expectation
'lavaan 0.6-19 ended normally after 334 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 55
Row rank of the constraints matrix 37
Number of observations 1997
Number of clusters [player_id] 397
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 13476.780 6885.368
Degrees of freedom 134 134
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.957
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 22341.153
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.922
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.688 0.696
Tucker-Lewis Index (TLI) 0.644 0.653
Robust Comparative Fit Index (CFI) 0.507
Robust Tucker-Lewis Index (TLI) 0.437
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -60738.707 -60738.707
Scaling correction factor 2.381
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 2.081
for the MLR correction
Akaike (AIC) 121587.413 121587.413
Bayesian (BIC) 121895.380 121895.380
Sample-size adjusted Bayesian (SABIC) 121720.643 121720.643
Root Mean Square Error of Approximation:
RMSEA 0.223 0.159
90 Percent confidence interval - lower 0.220 0.157
90 Percent confidence interval - upper 0.226 0.161
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 1.000 1.000
Robust RMSEA 0.454
90 Percent confidence interval - lower 0.436
90 Percent confidence interval - upper 0.472
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.343 0.343
Parameter Estimates:
Standard errors Robust.cluster
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~
completinsPrGm 7.900 0.122 64.949 0.000 7.900 0.987
attemptsPerGam 12.212 0.168 72.668 0.000 12.212 0.975
pssng_yrdsPrGm 92.101 1.471 62.601 0.000 92.101 0.994
passng_tdsPrGm 0.594 0.019 31.404 0.000 0.594 0.862
pssng_r_yrdsPG 83.486 3.587 23.277 0.000 83.486 0.691
pssng_yrds__PG 50.420 1.510 33.395 0.000 50.420 0.770
pssng_frst_dPG 4.495 0.079 57.239 0.000 4.495 0.992
F2 =~
avg_cmpltd_r_y 2.661 NA 2.661 0.951
avg_ntndd_r_yr 3.245 0.090 36.067 0.000 3.245 0.995
aggressiveness 4.684 0.645 7.257 0.000 4.684 0.702
mx_cmpltd_r_ds 6.873 0.563 12.209 0.000 6.873 0.817
avg_air_distnc 3.012 0.127 23.630 0.000 3.012 0.974
max_air_distnc 6.318 0.634 9.967 0.000 6.318 0.818
avg_r_yrds_t_s 3.255 NA 3.255 0.989
passing_cpoe 10.346 0.486 21.271 0.000 10.346 0.872
pass_comp_pct 0.109 0.005 22.026 0.000 0.109 0.842
passer_rating 7.181 2.706 2.653 0.008 7.181 0.396
cmpltn_prcnt__ 2.378 0.791 3.005 0.003 2.378 0.409
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 ~~
F2 0.283 0.040 7.112 0.000 0.283 0.283
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.391 33.868 0.000 13.257 1.657
.attemptsPerGam 21.899 0.581 37.714 0.000 21.899 1.748
.pssng_yrdsPrGm 148.475 4.622 32.121 0.000 148.475 1.602
.passng_tdsPrGm 0.850 0.036 23.842 0.000 0.850 1.234
.pssng_r_yrdsPG 133.536 5.766 23.158 0.000 133.536 1.105
.pssng_yrds__PG 87.878 2.982 29.472 0.000 87.878 1.342
.pssng_frst_dPG 7.166 0.228 31.455 0.000 7.166 1.581
.avg_cmpltd_r_y 5.110 0.111 46.052 0.000 5.110 1.826
.avg_ntndd_r_yr 7.248 0.136 53.337 0.000 7.248 2.223
.aggressiveness 15.430 0.353 43.690 0.000 15.430 2.313
.mx_cmpltd_r_ds 37.571 0.391 96.001 0.000 37.571 4.468
.avg_air_distnc 20.477 0.137 148.950 0.000 20.477 6.619
.max_air_distnc 46.154 0.409 112.855 0.000 46.154 5.977
.avg_r_yrds_t_s -1.714 0.132 -12.965 0.000 -1.714 -0.521
.passing_cpoe -3.269 0.375 -8.723 0.000 -3.269 -0.275
.pass_comp_pct 0.589 0.004 144.616 0.000 0.589 4.561
.passer_rating 83.867 1.225 68.468 0.000 83.867 4.626
.cmpltn_prcnt__ -1.517 0.360 -4.207 0.000 -1.517 -0.261
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 1.630 0.123 13.288 0.000 1.630 0.025
.attemptsPerGam 7.748 0.462 16.787 0.000 7.748 0.049
.pssng_yrdsPrGm 106.868 9.630 11.098 0.000 106.868 0.012
.passng_tdsPrGm 0.122 0.007 17.324 0.000 0.122 0.257
.pssng_r_yrdsPG 7625.681 0.352 21649.103 0.000 7625.681 0.522
.pssng_yrds__PG 1742.807 132.447 13.158 0.000 1742.807 0.407
.pssng_frst_dPG 0.344 0.027 12.931 0.000 0.344 0.017
.avg_cmpltd_r_y 0.749 0.078 9.588 0.000 0.749 0.096
.avg_ntndd_r_yr 0.097 0.027 3.538 0.000 0.097 0.009
.aggressiveness 22.575 2.997 7.532 0.000 22.575 0.507
.mx_cmpltd_r_ds 23.491 2.118 11.089 0.000 23.491 0.332
.avg_air_distnc 0.501 0.042 11.867 0.000 0.501 0.052
.max_air_distnc 19.727 2.181 9.044 0.000 19.727 0.331
.avg_r_yrds_t_s 0.230 0.039 5.854 0.000 0.230 0.021
.passing_cpoe 33.805 3.145 10.748 0.000 33.805 0.240
.pass_comp_pct 0.005 0.000 11.396 0.000 0.005 0.292
.passer_rating 277.145 23.550 11.768 0.000 277.145 0.843
.cmpltn_prcnt__ 28.150 2.897 9.719 0.000 28.150 0.833
F1 1.000 1.000 1.000
F2 1.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.975
attemptsPerGam 0.951
pssng_yrdsPrGm 0.988
passng_tdsPrGm 0.743
pssng_r_yrdsPG 0.478
pssng_yrds__PG 0.593
pssng_frst_dPG 0.983
avg_cmpltd_r_y 0.904
avg_ntndd_r_yr 0.991
aggressiveness 0.493
mx_cmpltd_r_ds 0.668
avg_air_distnc 0.948
max_air_distnc 0.669
avg_r_yrds_t_s 0.979
passing_cpoe 0.760
pass_comp_pct 0.708
passer_rating 0.157
cmpltn_prcnt__ 0.167The two-factor model did not fit well according to the fit indices:
Code
chisq df pvalue
13476.780 134.000 0.000
chisq.scaled df.scaled pvalue.scaled
6885.368 134.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.957 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.223 0.688
tli srmr rmsea.robust
0.644 0.343 0.454
cfi.robust tli.robust
0.507 0.437 $type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame 0.022 0.000
passing_yardsPerGame -0.003 -0.003 0.000
passing_tdsPerGame -0.024 -0.049 0.013 0.000
passing_air_yardsPerGame 0.012 0.009 0.004 -0.019
passing_yards_after_catchPerGame -0.008 0.014 0.011 0.007
passing_first_downsPerGame -0.002 -0.007 0.002 0.016
avg_completed_air_yards -0.387 -0.408 -0.353 -0.267
avg_intended_air_yards -0.431 -0.450 -0.412 -0.332
aggressiveness -0.366 -0.347 -0.363 -0.316
max_completed_air_distance 0.015 -0.005 0.051 0.096
avg_air_distance -0.463 -0.480 -0.445 -0.362
max_air_distance -0.072 -0.093 -0.067 -0.036
avg_air_yards_to_sticks -0.407 -0.428 -0.387 -0.299
passing_cpoe -0.047 -0.133 -0.054 0.003
pass_comp_pct 0.053 -0.033 0.035 0.070
passer_rating 0.235 0.147 0.260 0.363
completion_percentage_above_expectation 0.046 -0.042 0.036 0.074
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame -0.429 0.000
passing_first_downsPerGame 0.001 -0.002 0.000
avg_completed_air_yards 0.367 -0.847 -0.357 0.000
avg_intended_air_yards 0.366 -0.889 -0.412 0.006
aggressiveness 0.159 -0.630 -0.349 -0.036
max_completed_air_distance 0.452 -0.352 0.022 -0.096
avg_air_distance 0.312 -0.884 -0.450 -0.007
max_air_distance 0.503 -0.510 -0.080 -0.067
avg_air_yards_to_sticks 0.364 -0.854 -0.382 0.004
passing_cpoe 0.204 -0.301 -0.045 -0.549
pass_comp_pct 0.009 -0.011 0.045 -0.934
passer_rating 0.212 0.115 0.264 -0.333
completion_percentage_above_expectation 0.336 -0.294 0.047 0.002
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness -0.036 0.000
max_completed_air_distance -0.189 -0.222 0.000
avg_air_distance 0.005 -0.033 -0.166 0.000
max_air_distance -0.041 -0.129 0.101 -0.031 0.000
avg_air_yards_to_sticks 0.000 -0.034 -0.170 -0.002 -0.048
passing_cpoe -0.606 -0.678 -0.313 -0.612 -0.375
pass_comp_pct -1.008 -0.961 -0.570 -1.019 -0.669
passer_rating -0.408 -0.544 -0.020 -0.426 -0.172
completion_percentage_above_expectation -0.037 -0.201 0.116 -0.054 0.078
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe -0.595 0.000
pass_comp_pct -0.999 0.130 0.000
passer_rating -0.392 0.507 0.551 0.000
completion_percentage_above_expectation -0.034 0.606 0.450 0.630 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 -0.111
avg_intended_air_yards aggressiveness
-0.151 0.032
max_completed_air_distance avg_air_distance
-0.158 -0.107
max_air_distance avg_air_yards_to_sticks
-0.287 -0.127
passing_cpoe pass_comp_pct
-0.189 0.009
passer_rating completion_percentage_above_expectation
-0.210 -0.339 Below are factor scores from the model for the first six players:
F1 F2
[1,] -0.07860797 0.7872457
[2,] 0.15963421 -0.1818889
[3,] 0.42522065 -0.2978590
[4,] 0.10540880 0.6674248
[5,] 0.88641294 0.1166437
[6,] -0.07102630 -0.4041747The path diagram of the two-factor CFA model is in Figure 22.21.
Because the one-factor model is nested within the two-factor model, we can compare them using a chi-square difference test. The two factor model fit considerably better than the one-factor model in terms of a lower chi-square value:
Below is the syntax for the three-factor model:
Code
cfa3factor_syntax <- '
#Factor loadings
F1 =~ completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame
F2 =~ avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks
F3 =~ passing_cpoe + pass_comp_pct + passer_rating + completion_percentage_above_expectation
'lavaan 0.6-19 ended normally after 4554 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 57
Row rank of the constraints matrix 39
Number of observations 1997
Number of clusters [player_id] 397
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 10891.311 5784.359
Degrees of freedom 132 132
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.883
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 22341.153
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.922
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.749 0.745
Tucker-Lewis Index (TLI) 0.709 0.705
Robust Comparative Fit Index (CFI) 0.713
Robust Tucker-Lewis Index (TLI) 0.667
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -59445.973 -59445.973
Scaling correction factor 2.539
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 2.081
for the MLR correction
Akaike (AIC) 119005.945 119005.945
Bayesian (BIC) 119325.111 119325.111
Sample-size adjusted Bayesian (SABIC) 119144.019 119144.019
Root Mean Square Error of Approximation:
RMSEA 0.202 0.146
90 Percent confidence interval - lower 0.199 0.144
90 Percent confidence interval - upper 0.205 0.149
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 1.000 1.000
Robust RMSEA 0.349
90 Percent confidence interval - lower 0.331
90 Percent confidence interval - upper 0.368
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.324 0.324
Parameter Estimates:
Standard errors Robust.cluster
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~
completinsPrGm 7.904 0.121 65.467 0.000 7.904 0.987
attemptsPerGam 12.218 0.168 72.739 0.000 12.218 0.975
pssng_yrdsPrGm 92.158 1.463 62.997 0.000 92.158 0.994
passng_tdsPrGm 0.594 0.019 31.607 0.000 0.594 0.862
pssng_r_yrdsPG 83.535 3.579 23.342 0.000 83.535 0.691
pssng_yrds__PG 50.449 1.515 33.293 0.000 50.449 0.770
pssng_frst_dPG 4.498 0.078 57.603 0.000 4.498 0.992
F2 =~
avg_cmpltd_r_y 1.111 0.064 17.452 0.000 1.111 0.781
avg_ntndd_r_yr 1.388 0.064 21.820 0.000 1.388 0.992
aggressiveness 2.008 0.300 6.689 0.000 2.008 0.390
mx_cmpltd_r_ds 2.680 0.277 9.685 0.000 2.680 0.475
avg_air_distnc 1.273 0.066 19.210 0.000 1.273 0.877
max_air_distnc 2.618 0.298 8.778 0.000 2.618 0.506
avg_r_yrds_t_s 1.383 0.079 17.476 0.000 1.383 0.937
F3 =~
passing_cpoe 12.045 0.482 25.013 0.000 12.045 0.997
pass_comp_pct 0.119 0.005 24.550 0.000 0.119 0.919
passer_rating 25.689 25.689 0.919
cmpltn_prcnt__ 10.144 0.525 19.313 0.000 10.144 0.966
Covariances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 ~~
F2 0.154 0.076 2.035 0.042 0.154 0.154
F3 0.302 0.037 8.066 0.000 0.302 0.302
F2 ~~
F3 0.072 0.132 0.546 0.585 0.072 0.072
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.391 33.868 0.000 13.257 1.656
.attemptsPerGam 21.899 0.581 37.714 0.000 21.899 1.747
.pssng_yrdsPrGm 148.475 4.622 32.121 0.000 148.475 1.601
.passng_tdsPrGm 0.850 0.036 23.842 0.000 0.850 1.233
.pssng_r_yrdsPG 133.536 5.766 23.158 0.000 133.536 1.105
.pssng_yrds__PG 87.878 2.982 29.472 0.000 87.878 1.342
.pssng_frst_dPG 7.166 0.228 31.455 0.000 7.166 1.580
.avg_cmpltd_r_y 5.672 0.095 59.955 0.000 5.672 3.988
.avg_ntndd_r_yr 7.931 0.108 73.627 0.000 7.931 5.665
.aggressiveness 16.416 0.295 55.593 0.000 16.416 3.191
.mx_cmpltd_r_ds 39.038 0.340 114.654 0.000 39.038 6.919
.avg_air_distnc 21.112 0.104 203.240 0.000 21.112 14.550
.max_air_distnc 47.490 0.332 143.039 0.000 47.490 9.176
.avg_r_yrds_t_s -1.028 0.110 -9.352 0.000 -1.028 -0.696
.passing_cpoe -3.494 0.376 -9.298 0.000 -3.494 -0.289
.pass_comp_pct 0.589 0.004 144.213 0.000 0.589 4.533
.passer_rating 80.620 0.994 81.092 0.000 80.620 2.885
.cmpltn_prcnt__ -2.910 0.353 -8.251 0.000 -2.910 -0.277
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 1.635 0.123 13.303 0.000 1.635 0.026
.attemptsPerGam 7.773 0.461 16.856 0.000 7.773 0.049
.pssng_yrdsPrGm 106.416 9.610 11.074 0.000 106.416 0.012
.passng_tdsPrGm 0.122 0.007 17.325 0.000 0.122 0.257
.pssng_r_yrdsPG 7625.668 0.351 21697.485 0.000 7625.668 0.522
.pssng_yrds__PG 1742.886 132.443 13.160 0.000 1742.886 0.406
.pssng_frst_dPG 0.343 0.026 12.950 0.000 0.343 0.017
.avg_cmpltd_r_y 0.787 0.084 9.389 0.000 0.787 0.389
.avg_ntndd_r_yr 0.033 0.021 1.540 0.123 0.033 0.017
.aggressiveness 22.424 2.889 7.762 0.000 22.424 0.848
.mx_cmpltd_r_ds 24.649 2.207 11.168 0.000 24.649 0.774
.avg_air_distnc 0.484 0.037 13.026 0.000 0.484 0.230
.max_air_distnc 19.929 2.186 9.117 0.000 19.929 0.744
.avg_r_yrds_t_s 0.268 0.043 6.167 0.000 0.268 0.123
.passing_cpoe 0.908 1.098 0.827 0.408 0.908 0.006
.pass_comp_pct 0.003 0.000 7.732 0.000 0.003 0.155
.passer_rating 120.960 17.218 7.025 0.000 120.960 0.155
.cmpltn_prcnt__ 7.377 1.161 6.355 0.000 7.377 0.067
F1 1.000 1.000 1.000
F2 1.000 1.000 1.000
F3 1.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.974
attemptsPerGam 0.951
pssng_yrdsPrGm 0.988
passng_tdsPrGm 0.743
pssng_r_yrdsPG 0.478
pssng_yrds__PG 0.594
pssng_frst_dPG 0.983
avg_cmpltd_r_y 0.611
avg_ntndd_r_yr 0.983
aggressiveness 0.152
mx_cmpltd_r_ds 0.226
avg_air_distnc 0.770
max_air_distnc 0.256
avg_r_yrds_t_s 0.877
passing_cpoe 0.994
pass_comp_pct 0.845
passer_rating 0.845
cmpltn_prcnt__ 0.933The three-factor model did not fit well according to fit indices:
Code
chisq df pvalue
10891.311 132.000 0.000
chisq.scaled df.scaled pvalue.scaled
5784.359 132.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.883 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.202 0.749
tli srmr rmsea.robust
0.709 0.324 0.349
cfi.robust tli.robust
0.713 0.667 However, we know that the three-factor model fit improved considerably when accounting for correlated residuals. So, we plan to examine modification indices to see if we can account for covariances between variables that were not explained by their underlying latent factors.
$type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame 0.022 0.000
passing_yardsPerGame -0.003 -0.003 0.000
passing_tdsPerGame -0.024 -0.049 0.013 0.000
passing_air_yardsPerGame 0.012 0.009 0.004 -0.019
passing_yards_after_catchPerGame -0.008 0.014 0.010 0.007
passing_first_downsPerGame -0.002 -0.007 0.002 0.016
avg_completed_air_yards -0.240 -0.263 -0.205 -0.138
avg_intended_air_yards -0.303 -0.324 -0.284 -0.220
aggressiveness -0.229 -0.212 -0.225 -0.196
max_completed_air_distance 0.172 0.149 0.209 0.233
avg_air_distance -0.324 -0.342 -0.305 -0.240
max_air_distance 0.080 0.057 0.086 0.097
avg_air_yards_to_sticks -0.272 -0.295 -0.251 -0.182
passing_cpoe -0.101 -0.186 -0.108 -0.044
pass_comp_pct 0.014 -0.071 -0.004 0.036
passer_rating 0.071 -0.014 0.096 0.220
completion_percentage_above_expectation -0.128 -0.213 -0.139 -0.078
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame -0.429 0.000
passing_first_downsPerGame 0.000 -0.002 0.000
avg_completed_air_yards 0.470 -0.732 -0.209 0.000
avg_intended_air_yards 0.455 -0.789 -0.284 0.178
aggressiveness 0.255 -0.523 -0.212 0.327
max_completed_air_distance 0.562 -0.230 0.180 0.310
avg_air_distance 0.410 -0.775 -0.310 0.233
max_air_distance 0.610 -0.392 0.073 0.315
avg_air_yards_to_sticks 0.459 -0.749 -0.247 0.213
passing_cpoe 0.166 -0.343 -0.098 0.224
pass_comp_pct -0.018 -0.042 0.006 -0.185
passer_rating 0.098 -0.013 0.100 -0.008
completion_percentage_above_expectation 0.214 -0.429 -0.128 0.336
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness 0.276 0.000
max_completed_air_distance 0.153 0.166 0.000
avg_air_distance 0.104 0.308 0.213 0.000
max_air_distance 0.271 0.247 0.529 0.322 0.000
avg_air_yards_to_sticks 0.057 0.294 0.194 0.139 0.288
passing_cpoe 0.191 -0.094 0.365 0.174 0.302
pass_comp_pct -0.236 -0.396 0.086 -0.257 -0.014
passer_rating -0.080 -0.292 0.272 -0.099 0.118
completion_percentage_above_expectation 0.301 0.059 0.418 0.283 0.377
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe 0.200 0.000
pass_comp_pct -0.228 -0.053 0.000
passer_rating -0.062 -0.065 0.039 0.000
completion_percentage_above_expectation 0.306 0.000 -0.094 -0.096 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 -0.323
avg_intended_air_yards aggressiveness
-0.351 -0.117
max_completed_air_distance avg_air_distance
-0.370 -0.304
max_air_distance avg_air_yards_to_sticks
-0.465 -0.337
passing_cpoe pass_comp_pct
-0.173 0.012
passer_rating completion_percentage_above_expectation
-0.084 -0.219 Below are the modification indices, suggesting potential model modifications that would improve model fit such as correlated residuals and cross-loadings.
Below are factor scores from the model for the first six players:
F1 F2 F3
[1,] -0.07765670 0.01326596 0.8697502
[2,] 0.15942702 0.01740013 -0.2043168
[3,] 0.42439461 0.05197153 -0.3436464
[4,] 0.10579239 0.03359343 0.6454713
[5,] 0.88604619 0.13561583 0.2429619
[6,] -0.07133603 -0.02285548 -0.4424469The path diagram of the three-factor CFA model is in Figure 22.22.
Because the two-factor model is nested within the three-factor model, we can compare them using a chi-square difference test. The three factor model fit considerably better than the two-factor model in terms of a lower chi-square value:
Based on the model modifications suggested by the modification indices for the three-factor model, we modify the model to account for correlated residuals, using the syntax below:
Code
cfa3factorModified_syntax <- '
# Factor loadings
F1 =~ NA*completionsPerGame + attemptsPerGame + passing_yardsPerGame + passing_tdsPerGame +
passing_air_yardsPerGame + passing_yards_after_catchPerGame + passing_first_downsPerGame
F2 =~ NA*avg_completed_air_yards + avg_intended_air_yards + aggressiveness + max_completed_air_distance +
avg_air_distance + max_air_distance + avg_air_yards_to_sticks
F3 =~ NA*passing_cpoe + pass_comp_pct + passer_rating + completion_percentage_above_expectation
# Cross loadings
#F3 =~ attemptsPerGame
# Correlated residuals
passing_air_yardsPerGame ~~ passing_yards_after_catchPerGame
completionsPerGame ~~ attemptsPerGame
attemptsPerGame ~~ passing_yards_after_catchPerGame
passing_yards_after_catchPerGame ~~ passing_first_downsPerGame
completionsPerGame ~~ passing_first_downsPerGame
attemptsPerGame ~~ passing_tdsPerGame
completionsPerGame ~~ passing_tdsPerGame
passing_tdsPerGame ~~ passing_air_yardsPerGame
max_completed_air_distance ~~ max_air_distance
avg_completed_air_yards ~~ max_completed_air_distance
avg_completed_air_yards ~~ avg_air_distance
avg_completed_air_yards ~~ max_air_distance
avg_intended_air_yards ~~ max_completed_air_distance
completionsPerGame ~~ pass_comp_pct
passing_yardsPerGame ~~ avg_completed_air_yards
passing_yardsPerGame ~~ max_completed_air_distance
passing_tdsPerGame ~~ passer_rating
aggressiveness ~~ completion_percentage_above_expectation
# Variances
F1 ~~ 1*F1
F2 ~~ 1*F2
'lavaan 0.6-19 ended normally after 8537 iterations
Estimator ML
Optimization method NLMINB
Number of model parameters 76
Row rank of the constraints matrix 40
Number of observations 1997
Number of clusters [player_id] 397
Number of missing patterns 4
Model Test User Model:
Standard Scaled
Test Statistic 2226.535 1170.113
Degrees of freedom 113 113
P-value (Chi-square) 0.000 0.000
Scaling correction factor 1.903
Yuan-Bentler correction (Mplus variant)
Model Test Baseline Model:
Test statistic 42942.078 22341.153
Degrees of freedom 153 153
P-value 0.000 0.000
Scaling correction factor 1.922
User Model versus Baseline Model:
Comparative Fit Index (CFI) 0.951 0.952
Tucker-Lewis Index (TLI) 0.933 0.935
Robust Comparative Fit Index (CFI) 0.797
Robust Tucker-Lewis Index (TLI) 0.725
Loglikelihood and Information Criteria:
Loglikelihood user model (H0) -55113.584 -55113.584
Scaling correction factor 2.345
for the MLR correction
Loglikelihood unrestricted model (H1) -54000.317 -54000.317
Scaling correction factor 2.081
for the MLR correction
Akaike (AIC) 110379.168 110379.168
Bayesian (BIC) 110804.723 110804.723
Sample-size adjusted Bayesian (SABIC) 110563.267 110563.267
Root Mean Square Error of Approximation:
RMSEA 0.097 0.068
90 Percent confidence interval - lower 0.093 0.066
90 Percent confidence interval - upper 0.100 0.071
P-value H_0: RMSEA <= 0.050 0.000 0.000
P-value H_0: RMSEA >= 0.080 1.000 0.000
Robust RMSEA 0.317
90 Percent confidence interval - lower 0.296
90 Percent confidence interval - upper 0.339
P-value H_0: Robust RMSEA <= 0.050 0.000
P-value H_0: Robust RMSEA >= 0.080 1.000
Standardized Root Mean Square Residual:
SRMR 0.322 0.322
Parameter Estimates:
Standard errors Robust.cluster
Information Observed
Observed information based on Hessian
Latent Variables:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 =~
completinsPrGm 7.862 0.123 63.730 0.000 7.862 0.982
attemptsPerGam 12.158 0.171 70.949 0.000 12.158 0.968
pssng_yrdsPrGm 92.224 1.461 63.107 0.000 92.224 0.996
passng_tdsPrGm 0.595 0.018 32.321 0.000 0.595 0.872
pssng_r_yrdsPG 84.143 3.632 23.169 0.000 84.143 0.694
pssng_yrds__PG 51.005 1.527 33.409 0.000 51.005 0.778
pssng_frst_dPG 4.500 0.079 56.755 0.000 4.500 0.991
F2 =~
avg_cmpltd_r_y 1.107 0.061 18.103 0.000 1.107 0.809
avg_ntndd_r_yr 1.389 0.065 21.370 0.000 1.389 0.986
aggressiveness 1.733 0.297 5.829 0.000 1.733 0.343
mx_cmpltd_r_ds 2.871 0.280 10.256 0.000 2.871 0.507
avg_air_distnc 1.284 0.067 19.212 0.000 1.284 0.881
max_air_distnc 2.647 0.302 8.770 0.000 2.647 0.511
avg_r_yrds_t_s 1.399 0.080 17.492 0.000 1.399 0.942
F3 =~
passing_cpoe 2.665 0.113 23.593 0.000 12.149 0.990
pass_comp_pct 0.026 0.001 20.620 0.000 0.117 0.927
passer_rating 6.050 0.437 13.836 0.000 27.578 0.937
cmpltn_prcnt__ 2.404 0.130 18.528 0.000 10.957 0.974
Covariances:
Estimate Std.Err z-value P(>|z|)
.passing_air_yardsPerGame ~~
.pssng_yrds__PG -3502.485 26.180 -133.784 0.000
.completionsPerGame ~~
.attemptsPerGam 3.507 0.186 18.820 0.000
.attemptsPerGame ~~
.pssng_yrds__PG 15.530 1.041 14.915 0.000
.passing_yards_after_catchPerGame ~~
.pssng_frst_dPG -3.439 0.280 -12.301 0.000
.completionsPerGame ~~
.pssng_frst_dPG 0.127 0.027 4.716 0.000
.attemptsPerGame ~~
.passng_tdsPrGm -0.438 0.035 -12.565 0.000
.completionsPerGame ~~
.passng_tdsPrGm -0.153 0.015 -10.453 0.000
.passing_tdsPerGame ~~
.pssng_r_yrdsPG -2.834 0.301 -9.418 0.000
.max_completed_air_distance ~~
.max_air_distnc 11.322 1.522 7.438 0.000
.avg_completed_air_yards ~~
.mx_cmpltd_r_ds 1.266 0.234 5.413 0.000
.avg_air_distnc -0.111 0.024 -4.713 0.000
.max_air_distnc -0.404 0.150 -2.696 0.007
.avg_intended_air_yards ~~
.mx_cmpltd_r_ds -0.460 0.135 -3.412 0.001
.completionsPerGame ~~
.pass_comp_pct 0.020 0.002 11.084 0.000
.passing_yardsPerGame ~~
.avg_cmpltd_r_y 4.803 0.319 15.068 0.000
.mx_cmpltd_r_ds 17.208 1.452 11.850 0.000
.passing_tdsPerGame ~~
.passer_rating 1.315 0.135 9.770 0.000
.aggressiveness ~~
.cmpltn_prcnt__ 5.703 1.037 5.499 0.000
F1 ~~
F2 0.224 0.072 3.091 0.002
F3 1.427 0.171 8.332 0.000
F2 ~~
F3 0.408 0.604 0.677 0.499
Std.lv Std.all
-3502.485 -0.973
3.507 0.728
15.530 0.119
-3.439 -0.136
0.127 0.137
-0.438 -0.415
-0.153 -0.300
-2.834 -0.097
11.322 0.521
1.266 0.322
-0.111 -0.201
-0.404 -0.113
-0.460 -0.405
0.020 0.274
4.803 0.687
17.208 0.406
1.315 0.382
5.703 0.469
0.224 0.224
0.313 0.313
0.090 0.090
Intercepts:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
.completinsPrGm 13.257 0.391 33.868 0.000 13.257 1.655
.attemptsPerGam 21.899 0.581 37.714 0.000 21.899 1.743
.pssng_yrdsPrGm 148.475 4.622 32.121 0.000 148.475 1.603
.passng_tdsPrGm 0.850 0.036 23.842 0.000 0.850 1.245
.pssng_r_yrdsPG 133.536 5.766 23.158 0.000 133.536 1.102
.pssng_yrds__PG 87.878 2.982 29.472 0.000 87.878 1.340
.pssng_frst_dPG 7.166 0.228 31.455 0.000 7.166 1.578
.avg_cmpltd_r_y 5.646 0.090 62.992 0.000 5.646 4.125
.avg_ntndd_r_yr 7.886 0.104 75.535 0.000 7.886 5.600
.aggressiveness 16.380 0.292 56.193 0.000 16.380 3.243
.mx_cmpltd_r_ds 38.966 0.342 113.789 0.000 38.966 6.885
.avg_air_distnc 21.069 0.101 208.558 0.000 21.069 14.454
.max_air_distnc 47.401 0.331 143.259 0.000 47.401 9.145
.avg_r_yrds_t_s -1.075 0.107 -10.010 0.000 -1.075 -0.724
.passing_cpoe -3.322 0.376 -8.846 0.000 -3.322 -0.271
.pass_comp_pct 0.589 0.004 143.914 0.000 0.589 4.684
.passer_rating 80.685 1.150 70.138 0.000 80.685 2.740
.cmpltn_prcnt__ -2.939 0.370 -7.946 0.000 -2.939 -0.261
Variances:
Estimate Std.Err z-value P(>|z|) Std.lv Std.all
F1 1.000 1.000 1.000
F2 1.000 1.000 1.000
.completinsPrGm 2.322 0.112 20.801 0.000 2.322 0.036
.attemptsPerGam 9.986 0.449 22.263 0.000 9.986 0.063
.pssng_yrdsPrGm 75.344 6.410 11.753 0.000 75.344 0.009
.passng_tdsPrGm 0.112 0.007 17.058 0.000 0.112 0.240
.pssng_r_yrdsPG 7606.994 17.588 432.499 0.000 7606.994 0.518
.pssng_yrds__PG 1701.882 28.112 60.539 0.000 1701.882 0.395
.pssng_frst_dPG 0.374 0.029 12.748 0.000 0.374 0.018
.avg_cmpltd_r_y 0.648 0.064 10.190 0.000 0.648 0.346
.avg_ntndd_r_yr 0.054 0.020 2.662 0.008 0.054 0.027
.aggressiveness 22.513 2.923 7.701 0.000 22.513 0.882
.mx_cmpltd_r_ds 23.792 1.954 12.173 0.000 23.792 0.743
.avg_air_distnc 0.476 0.037 12.804 0.000 0.476 0.224
.max_air_distnc 19.859 2.180 9.111 0.000 19.859 0.739
.avg_r_yrds_t_s 0.247 0.038 6.533 0.000 0.247 0.112
.passing_cpoe 2.877 1.254 2.294 0.022 2.877 0.019
.pass_comp_pct 0.002 0.002 0.141
.passer_rating 106.300 15.497 6.859 0.000 106.300 0.123
.cmpltn_prcnt__ 6.565 1.003 6.543 0.000 6.565 0.052
F3 20.779 0.070 294.800 0.000 1.000 1.000
R-Square:
Estimate
completinsPrGm 0.964
attemptsPerGam 0.937
pssng_yrdsPrGm 0.991
passng_tdsPrGm 0.760
pssng_r_yrdsPG 0.482
pssng_yrds__PG 0.605
pssng_frst_dPG 0.982
avg_cmpltd_r_y 0.654
avg_ntndd_r_yr 0.973
aggressiveness 0.118
mx_cmpltd_r_ds 0.257
avg_air_distnc 0.776
max_air_distnc 0.261
avg_r_yrds_t_s 0.888
passing_cpoe 0.981
pass_comp_pct 0.859
passer_rating 0.877
cmpltn_prcnt__ 0.948The three-factor model with correlated residuals fit was acceptable according to CFI and TLI. The model fit was subpar for RMSEA and SRMR.
Code
chisq df pvalue
2226.535 113.000 0.000
chisq.scaled df.scaled pvalue.scaled
1170.113 113.000 0.000
chisq.scaling.factor baseline.chisq baseline.df
1.903 42942.078 153.000
baseline.pvalue rmsea cfi
0.000 0.097 0.951
tli srmr rmsea.robust
0.933 0.322 0.317
cfi.robust tli.robust
0.797 0.725 $type
[1] "cor.bollen"
$cov
cmplPG attmPG pssng_yPG pssng_tPG
completionsPerGame 0.000
attemptsPerGame -0.001 0.000
passing_yardsPerGame 0.001 0.002 0.000
passing_tdsPerGame -0.001 -0.001 0.001 0.000
passing_air_yardsPerGame 0.013 0.011 0.000 0.006
passing_yards_after_catchPerGame -0.011 -0.007 0.002 -0.007
passing_first_downsPerGame 0.001 0.001 0.001 0.007
avg_completed_air_yards -0.299 -0.321 -0.304 -0.192
avg_intended_air_yards -0.369 -0.389 -0.352 -0.281
aggressiveness -0.245 -0.228 -0.242 -0.211
max_completed_air_distance 0.133 0.111 0.136 0.197
avg_air_distance -0.384 -0.401 -0.367 -0.296
max_air_distance 0.044 0.022 0.049 0.064
avg_air_yards_to_sticks -0.337 -0.359 -0.318 -0.241
passing_cpoe -0.108 -0.192 -0.117 -0.055
pass_comp_pct -0.016 -0.081 -0.017 0.022
passer_rating 0.058 -0.027 0.080 0.139
completion_percentage_above_expectation -0.139 -0.224 -0.152 -0.092
pssng_r_PG p___PG pssng_f_PG avg_c__
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame 0.000
passing_yards_after_catchPerGame 0.004 0.000
passing_first_downsPerGame -0.002 0.003 0.000
avg_completed_air_yards 0.428 -0.780 -0.269 0.000
avg_intended_air_yards 0.407 -0.843 -0.351 0.155
aggressiveness 0.243 -0.536 -0.228 0.354
max_completed_air_distance 0.534 -0.262 0.140 0.108
avg_air_distance 0.366 -0.824 -0.372 0.262
max_air_distance 0.584 -0.421 0.037 0.355
avg_air_yards_to_sticks 0.412 -0.802 -0.313 0.183
passing_cpoe 0.160 -0.351 -0.107 0.208
pass_comp_pct -0.028 -0.053 -0.006 -0.201
passer_rating 0.086 -0.027 0.085 -0.024
completion_percentage_above_expectation 0.204 -0.441 -0.140 0.320
avg_n__ aggrss mx_c__ avg_r_ mx_r_d
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards 0.000
aggressiveness 0.325 0.000
max_completed_air_distance 0.182 0.178 0.000
avg_air_distance 0.105 0.348 0.183 0.000
max_air_distance 0.269 0.270 0.124 0.316 0.000
avg_air_yards_to_sticks 0.056 0.337 0.160 0.131 0.280
passing_cpoe 0.175 -0.096 0.354 0.159 0.293
pass_comp_pct -0.252 -0.398 0.076 -0.272 -0.023
passer_rating -0.097 -0.294 0.261 -0.114 0.109
completion_percentage_above_expectation 0.284 -0.044 0.406 0.267 0.368
av____ pssng_ pss_c_ pssr_r cmp___
completionsPerGame
attemptsPerGame
passing_yardsPerGame
passing_tdsPerGame
passing_air_yardsPerGame
passing_yards_after_catchPerGame
passing_first_downsPerGame
avg_completed_air_yards
avg_intended_air_yards
aggressiveness
max_completed_air_distance
avg_air_distance
max_air_distance
avg_air_yards_to_sticks 0.000
passing_cpoe 0.184 0.000
pass_comp_pct -0.244 -0.054 0.000
passer_rating -0.079 -0.076 0.016 0.000
completion_percentage_above_expectation 0.289 -0.002 -0.108 -0.120 0.000
$mean
completionsPerGame attemptsPerGame
0.000 0.000
passing_yardsPerGame passing_tdsPerGame
0.000 0.000
passing_air_yardsPerGame passing_yards_after_catchPerGame
0.000 0.000
passing_first_downsPerGame avg_completed_air_yards
0.000 -0.313
avg_intended_air_yards aggressiveness
-0.338 -0.112
max_completed_air_distance avg_air_distance
-0.360 -0.291
max_air_distance avg_air_yards_to_sticks
-0.453 -0.323
passing_cpoe pass_comp_pct
-0.186 0.011
passer_rating completion_percentage_above_expectation
-0.086 -0.217 Below are factor scores from the model for the first six players:
Code
F1 F2 F3
[1,] 0.15200282 0.05356329 4.3317332
[2,] 0.15623732 0.03110551 -0.5903088
[3,] 0.23959954 0.04849106 -0.7391809
[4,] 0.10324204 0.03623227 2.9108905
[5,] 0.97290979 0.21576230 0.9697629
[6,] -0.01518718 -0.01281245 -2.0036753The path diagram of the modified three-factor CFA model with correlated residuals is in Figure 22.23.
Here are the variables that loaded onto each of the factors:
Code
factor1vars <- c(
"completionsPerGame","attemptsPerGame","passing_yardsPerGame","passing_tdsPerGame",
"passing_air_yardsPerGame","passing_yards_after_catchPerGame","passing_first_downsPerGame")
factor2vars <- c(
"avg_completed_air_yards","avg_intended_air_yards","aggressiveness","max_completed_air_distance",
"avg_air_distance","max_air_distance","avg_air_yards_to_sticks")
factor3vars <- c(
"passing_cpoe","pass_comp_pct","passer_rating","completion_percentage_above_expectation")The variables that loaded most strongly onto factor 1 appear to reflect Quarterback usage: completions per game, passing attempts per game, passing yards per game, passing touchdowns per game, passing air yards (total horizontal distance the ball travels on all pass attempts) per game, passing yards after the catch per game, and first downs gained per game by passing. Quarterbacks who tend to throw more tend to have higher levels on those variables. Thus, we label component 1 as “Usage”, which reflects total Quarterback involvement, regardless of efficiency or outcome.
The variables that loaded most strongly onto factor 2 appear to reflect Quarterback aggressiveness: average air yards on completed passes, average air yards on all attempted passes, aggressiveness (percentage of passing attempts thrown into tight windows, where there is a defender within one yard or less of the receiver at the time of the completion or incompletion), average amount of air yards ahead of or behind the first down marker on passing attempts, average air distance (the true three-dimensional distance the ball travels in the air), maximum air distance, and maximum air distance on completed passes. Quarterbacks who throw the ball farther and into tighter windows tend to have higher values on those variables. Thus, we label component 2 as “Aggressiveness”, which reflects throwing longer, more difficult passes with a tight window.
The variables that loaded most strongly onto factor 3 appear to reflect Quarterback performance: passing completion percentage above expectation, pass completion percentage, and passer rating. Quarterbacks who perform better tend to have higher values on those variables. Thus, we label component 3 as “Performance”.
Here are the players and seasons that showed the highest levels of Quarterback “Usage”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Usage”:
Code
Here are the players and seasons that showed the highest levels of Quarterback “Aggressiveness”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Aggressiveness”:
Code
Here are the players and seasons that showed the highest levels of Quarterback “Performance”:
Code
If we restrict it to Quarterbacks who played at least 10 games in the season, here are the players and seasons that showed the highest levels of Quarterback “Performance”:
Code
Here are the players and seasons that showed the lowest levels of Quarterback “Performance”:
Code
If we restrict it to Quarterbacks who played at least 10 games in the season, here are the players and seasons that showed the lowest levels of Quarterback “Performance”:
22.8 Conclusion
Factor analysis is a class of latent variable models that aims to identify the optimal, parsimonious latent structure for a group of variables. Latent variables are ways of studying and operationalizing theoretical constructs that cannot be directly observed or quantified. Factor analysis encompasses two general types: confirmatory factor analysis and exploratory factor analysis. Exploratory factor analysis (EFA) is used when the researcher has no a priori hypotheses about how a set of variables is structured. Confirmatory factor analysis (CFA) is used when a researcher wants to evaluate how well a hypothesized model fits. A goal of factor analysis is to balance accuracy (i.e., variance accounted for) and parsimony (i.e., simplicity). Factor analysis estimates the latent factors as the common variance among the variables that load onto that factor and discards the remaining variance as “error”. There are many decisions to make in factor analysis. These decisions can have important impacts on the resulting solution. Thus, it can be helpful for theory and interpretability to help guide decision-making when conducting factor analysis. Using both exploratory and confirmatory factor analysis, we were able to identify three latent factors that accounted for considerable variance in the variables we examined, pertaining to Quarterbacks: 1) usage; 2) aggressiveness; 3) performance. We were then able to determine which players were highest and lowest on each of these factors.
22.9 Session Info
R version 4.5.1 (2025-06-13)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.3 LTS
Matrix products: default
BLAS: /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so; LAPACK version 3.12.0
locale:
[1] LC_CTYPE=C.UTF-8 LC_NUMERIC=C LC_TIME=C.UTF-8
[4] LC_COLLATE=C.UTF-8 LC_MONETARY=C.UTF-8 LC_MESSAGES=C.UTF-8
[7] LC_PAPER=C.UTF-8 LC_NAME=C LC_ADDRESS=C
[10] LC_TELEPHONE=C LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C
time zone: UTC
tzcode source: system (glibc)
attached base packages:
[1] stats graphics grDevices utils datasets methods base
other attached packages:
[1] lubridate_1.9.4 forcats_1.0.0 stringr_1.5.2 dplyr_1.1.4
[5] purrr_1.1.0 readr_2.1.5 tidyr_1.3.1 tibble_3.3.0
[9] ggplot2_4.0.0 tidyverse_2.0.0 lavaanPlot_0.8.1 lavaan_0.6-19
[13] nFactors_2.4.1.2 psych_2.5.6
loaded via a namespace (and not attached):
[1] GPArotation_2025.3-1 DiagrammeR_1.0.11 generics_0.1.4
[4] stringi_1.8.7 lattice_0.22-7 hms_1.1.3
[7] digest_0.6.37 magrittr_2.0.4 evaluate_1.0.5
[10] grid_4.5.1 timechange_0.3.0 RColorBrewer_1.1-3
[13] fastmap_1.2.0 jsonlite_2.0.0 scales_1.4.0
[16] pbivnorm_0.6.0 numDeriv_2016.8-1.1 mnormt_2.1.1
[19] cli_3.6.5 rlang_1.1.6 visNetwork_2.1.4
[22] withr_3.0.2 yaml_2.3.10 tools_4.5.1
[25] parallel_4.5.1 tzdb_0.5.0 vctrs_0.6.5
[28] R6_2.6.1 stats4_4.5.1 lifecycle_1.0.4
[31] htmlwidgets_1.6.4 MASS_7.3-65 pkgconfig_2.0.3
[34] pillar_1.11.0 gtable_0.3.6 glue_1.8.0
[37] xfun_0.53 tidyselect_1.2.1 rstudioapi_0.17.1
[40] knitr_1.50 farver_2.1.2 htmltools_0.5.8.1
[43] nlme_3.1-168 rmarkdown_2.29 compiler_4.5.1
[46] quadprog_1.5-8 S7_0.2.0