I need your help!

I want your feedback to make the book better for you and other readers. If you find typos, errors, or places where the text may be improved, please let me know. The best ways to provide feedback are by GitHub or hypothes.is annotations.

Opening an issue or submitting a pull request on GitHub: https://github.com/isaactpetersen/Fantasy-Football-Analytics-Textbook

Hypothesis Adding an annotation using hypothes.is. To add an annotation, select some text and then click the symbol on the pop-up menu. To see the annotations of others, click the symbol in the upper right-hand corner of the page.

13  Causal Inference

13.1 Getting Started

13.1.1 Load Packages

Code
library("dagitty")
library("ggdag")

13.2 Correlation Does Not Imply Causation

As described in Section 8.4.2.1, there are several reasons why two variables, X and Y, might be correlated:

  • X causes Y
  • Y causes X
  • X and Y are bidirectional: X causes Y and Y causes X
  • a third variable (i.e., confound), Z, influences both X and Y
  • the association between X and Y is spurious

13.3 Criteria for Causality

How do we know whether two processes are causally related? There are three criteria for establishing causality (Shadish et al., 2002):

  1. The cause (e.g., the independent or predictor variable) temporally precedes the effect (i.e., the dependent or outcome variable).
  2. The cause is related to (i.e., associated with) the effect.
  3. There are no other alternative explanations for the effect apart from the cause.

The first criterion for establishing causality involves temporal precedence. In order for a cause to influence an effect, the cause must occur before the effect. For instance, if sports drink consumption influences player performance, the sports drink consumption (that is presumed to influence performance) must occur prior to the performance improvement. Establishing the first criterion eliminates the possibility that the association between the purported cause and effect reflects reverse causation. Reverse causation occurs when the purported effect is actually the cause of the purported cause, rather than the other way around. For instance, if sports drink consumption occurs only once, and it occurs only before and not after performance, then we have ruled out the possibility of reverse causation (i.e., that better performance causes players to consume sports drink).

The second criterion involves association. The purported cause must be associated with the purported effect. Nevertheless, as the maxim goes, “correlation does not imply causation.” Just because two variables are correlated does not necessarily mean that they are causally related. However, correlation is useful because causality requires that the two processes be correlated. That is, correlation is a necessary but insufficient condition for causality. For instance, if sports drink consumption influences player performance, sports drink consumption must be associated with performance improvement.

The third criterion involves ruling out alternative reasons why the purported cause and effect may be related. As noted in Section 13.2, there are four reasons why X may be correlated with Y. If we meet the first criterion of causality, we have removed the possibility that Y causes X (i.e., reverse causality). To meet the third criterion of causality, we need to remove the possibility that the association reflects a third variable (confound) that influences both the cause and effect, and we need to remove the possibility that the association is spurious—the possibility that the association between the purported cause and effect is due to random chance.

There are multiple approaches to meeting the third criterion of causality, such as by use of experiments, longitudinal designs, control variables, within-subject designs, and genetically informed designs, as described in Section 13.4.

In general, to meet the third criterion of causality, one must consider the counterfactual. A counterfactual is what would have happened in the hypothetical scenario that the cause did not occur [i.e., what would have happened in the absence of the cause; Shadish et al. (2002)]. When engaging in causal inference, it is important to consider what would have happened if the hypothetical cause had actually not occurred. For instance, consider that we conduct an experiment to randomly assign some players to consume a sports drink before a game and other players to drink only water. In this case, our treatment/intervention group is the group of players that consumed a sports drink. The control group is the group players that drank only water. Now, consider that the players in the treatment group outperform the players in the the control group in their football game. In such a study, we observe what did happen when players received a treatment. The counterfactual is knowledge of what would have happened to those same players if they simultaneously had not received treatment (Shadish et al., 2002). The true causal effect, then, is the difference between what did happen and what would have happened. However, we cannot observe a counterfactual. That is, we do not know for sure what would have happened to the players who received treatment if those same players had actually not received treatment. We have a control group, but the control group does not have the same players as the intervention group, and it is impossible for a person to simultaneously receive and not receive treatment.

So, our goal in working toward causal inference as scientists is to create reasonable approximations to this impossible counterfactual (Shadish et al., 2002). For instance, if using a between-subject design, we want the two groups to be equivalent in every possible way except whether or not they receive the treatment, so we might stratify each group to be equivalent in terms of age, weight, position, experience, skill, etc. Or, we might test the same people using an A-B-A-B within-subject design. In an A-B-A-B within-subject design, players receive no treatment at baseline (timepoint 1: game 1), receive the treatment at timepoint 2 (game 2), receive no treatment at timepoint 3 (game 3), and receive the treatment at timepoint 4 (game 4). Neither of these approximations is a true counterfactual. In the between-subject design, the players differ between the two groups, so we cannot know how the individuals who received the treatment would have performed if they had actually not received the treatment. In the A-B-A-B within-subject design, the players are the same, but they timepoints that they receive or do not receive the treatment differ, and there can be carryover effects from one condition to the next. For instance, consuming sports drinks before game 2 might also help them be better hydrated in general, including, for subsequent games. Thus, we cannot know how a player would have performed in game 1 with treatment or in game 2 without treatment, etc. Nevertheless, it is important to be aware of the counterfactual and to engage in counterfactual reasoning to consider what would have happened if the supposed cause had not occurred. Considering the counterfactual is important for designing closer approximations to the counterfactual in studies for stronger research designs and stronger causal inference.

13.4 Approaches for Causal Inference

13.4.1 Experimental Designs

As described in Section 8.4.1, experimental designs are designs in which participants are randomly assigned to one or more levels of the independent variable to observe its effects on the dependent variable. Experimental designs provide the strongest tests of causality because they can rule out reverse causation and third variables. For instance, by manipulating sports drink consumption before the player performs, they can eliminate the possibility that reverse causation explains the effect of the independent variable on the dependent variable. Second, through randomly assigning players to consume or not consume sports drink, this holds everything else constant (so long as the groups are evenly distributed according to other factors, such as their age, weight, etc.) and thus removes the possibility that third variable confounds explain the effect of the independent variable on the dependent variable.

13.4.2 Quasi-Experimental Designs

Although experimental designs provide the strongest tests of causality, manytimes they are impossible, unethical, or impractical to conduct. For instance, it would likely not be practical to randomly assign National Football League (NFL) players to either consume or not consume sports drink before their games. Players have their pregame rituals and routines and many would likely not agree to participate in such a study. Thus, we often rely on quasi-experimental designs such as natural experiments and observational/correlational designs.

We cannot directly test or establish causality from a non-experimental research design. Nevertheless, we can leverage various design features that, in combination with other studies using different research methods, collectively strengthen our ability to make causal inferences. For instance, there are are no experiments in humans showing that smoking causes cancer—randomly assigning people to smoke or not smoke would not be ethical. The causal inference that smoking causes cancer was derived from a combination of experimental studies in rodents and observational studies in humans.

13.4.2.1 Longitudinal Designs

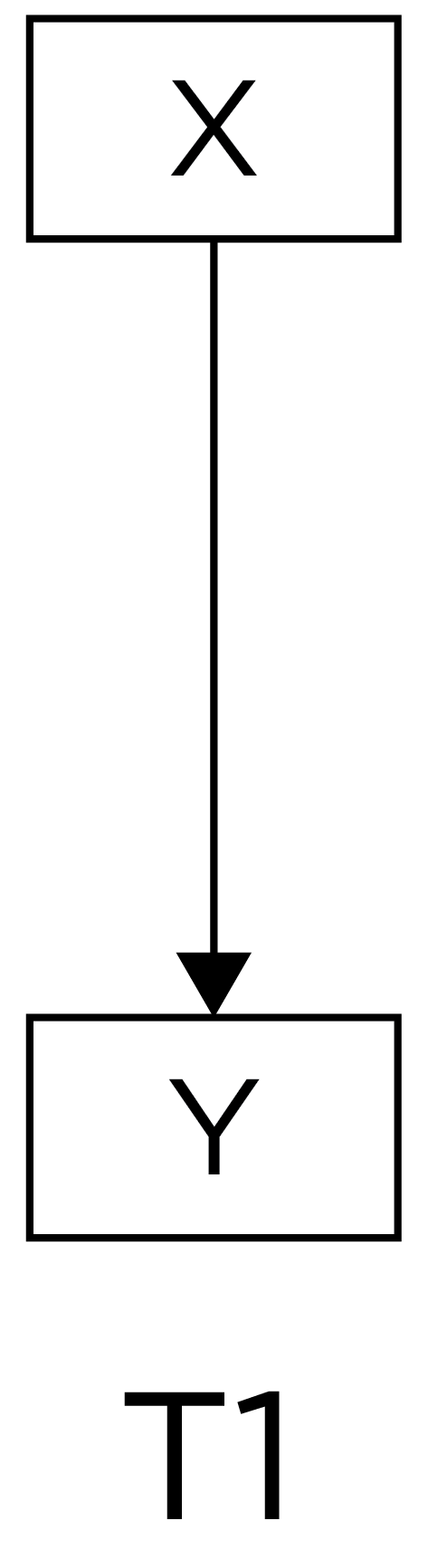
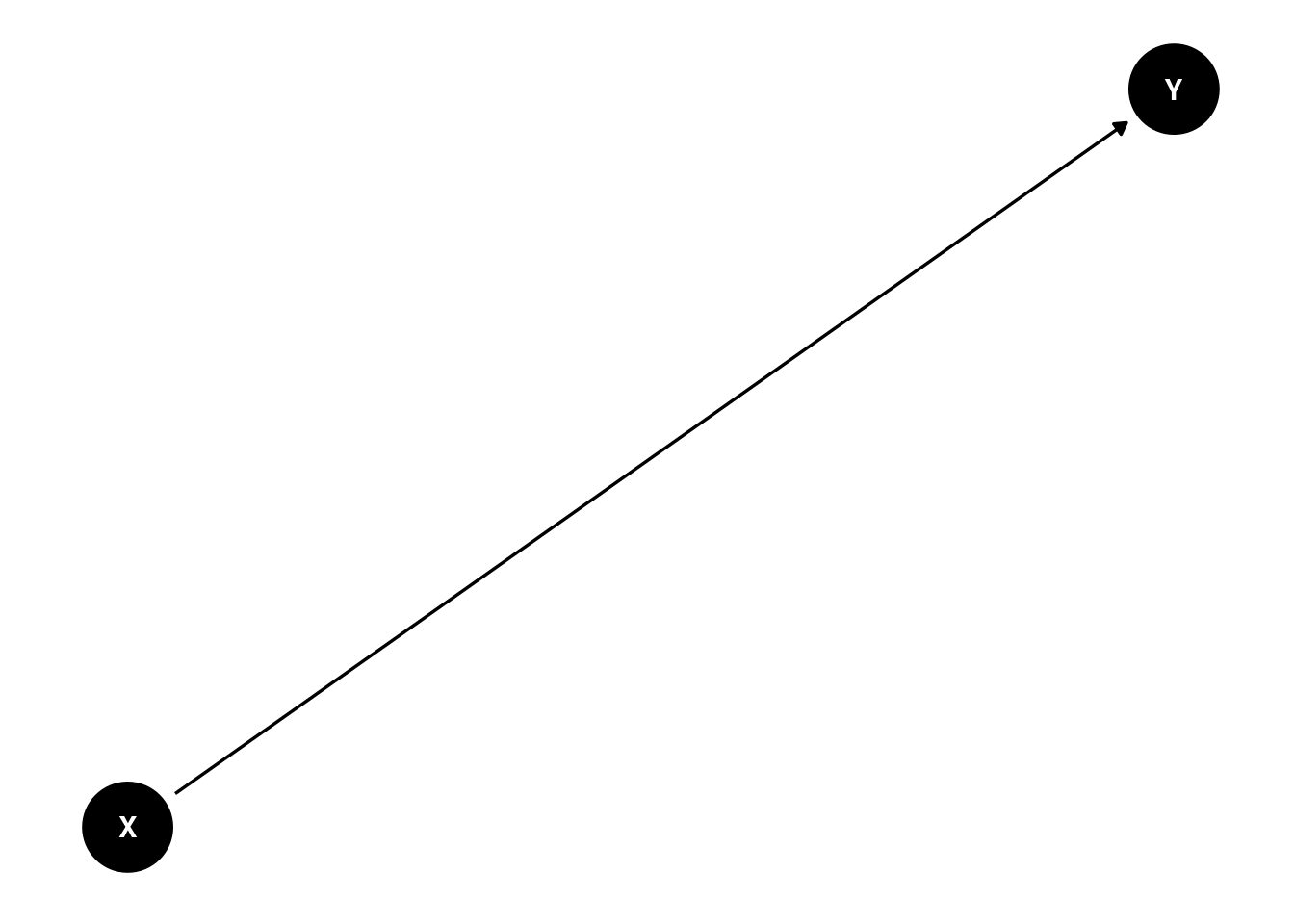
Research designs can be compared in terms of their internal validity—the extent to which we can be confident about causal inferences. A cross-sectional association is depicted in Figure 13.1:

Cross-Sectional Association. T1 = Timepoint 1. From @Petersen2024a and @PetersenPrinciplesPsychAssessment.
Figure 13.1: Cross-Sectional Association. T1 = Timepoint 1. From Petersen (2024a) and Petersen (2024b).

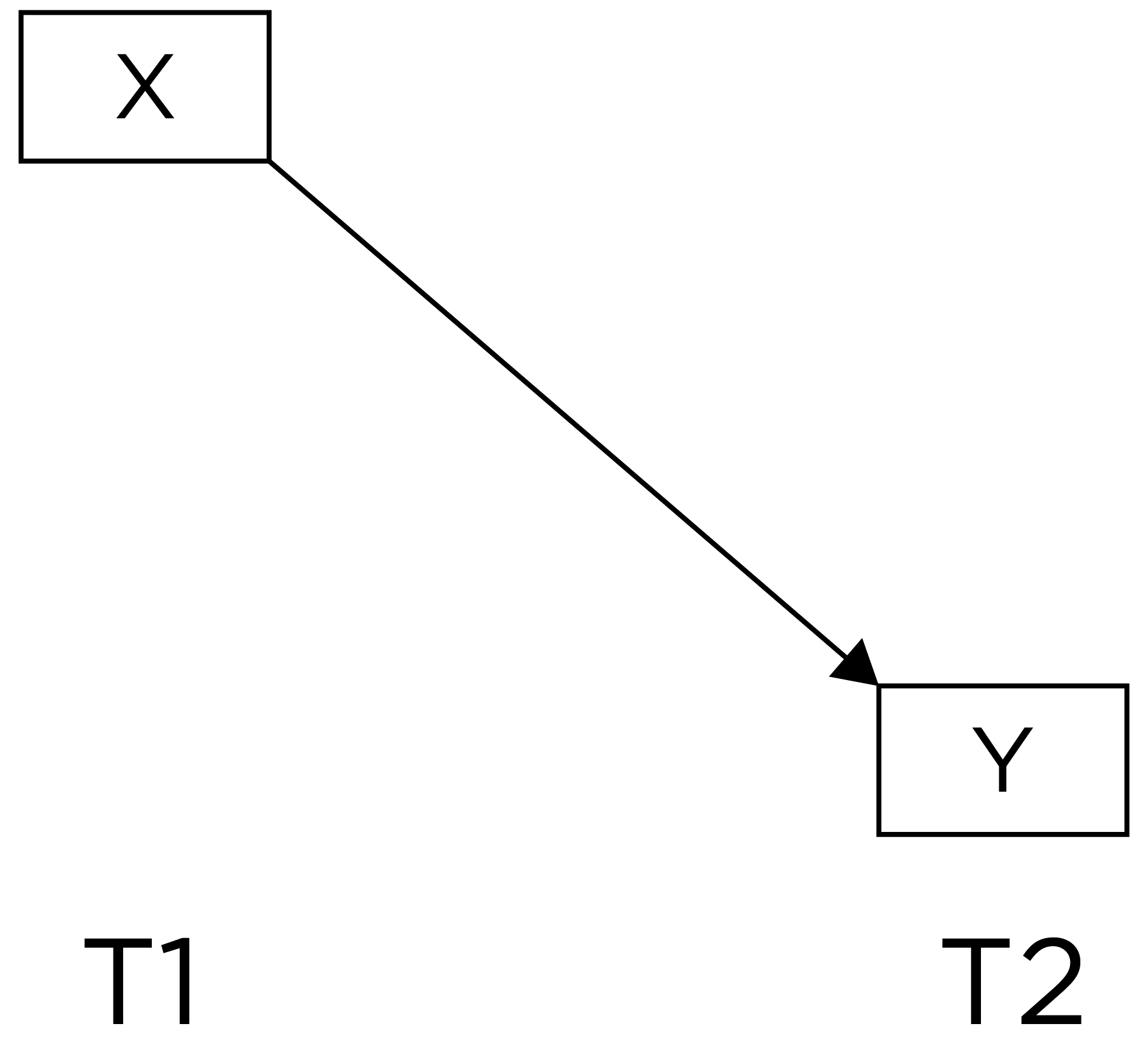
For instance, we might observe that sports drink consumptions is concurrently associated with better player performance. Among observational/correlational research designs, cross-sectional designs tend to have the weakest internal validity. For the reasons described in Section 13.2, if we observe a cross-sectional association between X (e.g., sports drink consumption) and Y (e.g., player performance), we have little confidence that X causes Y. As a result, longitudinal designs can be valuable for more closely approximating causality if an experimental designs is not possible. Consider a lagged association that might be observed in a longitudinal design, as in Figure 13.2, which is a slightly better approach than relying on cross-sectional associations:

Lagged Association. T1 = Timepoint 1. T2 = Timepoint 2. From @Petersen2024a and @PetersenPrinciplesPsychAssessment.
Figure 13.2: Lagged Association. T1 = Timepoint 1. T2 = Timepoint 2. From Petersen (2024a) and Petersen (2024b).

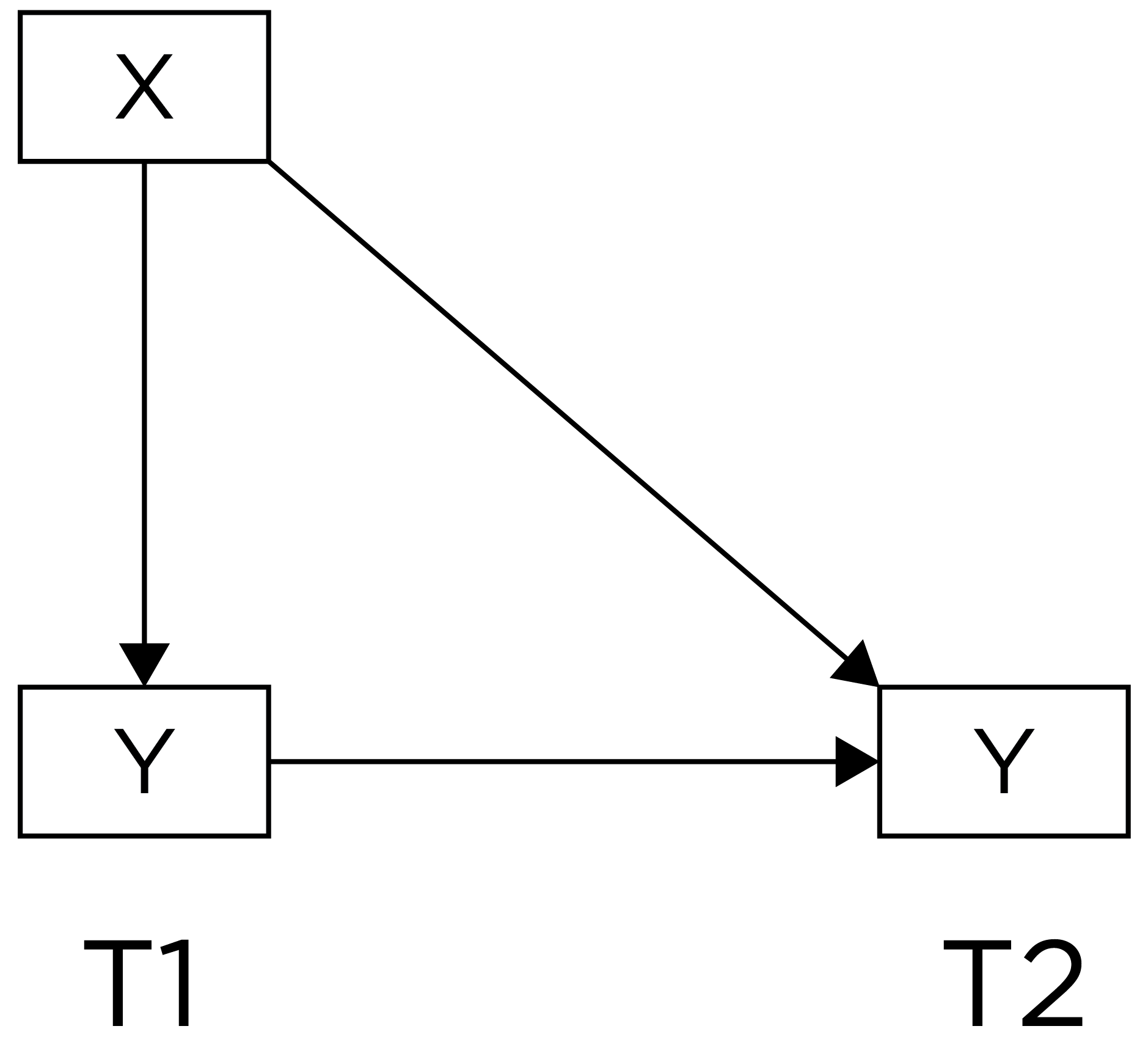
For instance, we might observe that sports drink performance before the game is associated with better player performance during the game. A lagged association has somewhat better internal validity than a cross-sectional association because we have greater evidence of temporal precedence—that the influence of the predictor precedes the outcome because the predictor was assessed before the outcome and it shows a predictive association. However, part of the association between the predictor with later levels of the outcome could be due to prior levels of the outcome that are stable across time. That is, it could be that better player performance leads players to consume more sports drink and that player performance is relatively stable across time. In such a case, it may be observed that sports drink consumption predicts later player performance even though player performance influences sports drink consumption, rather than the other way around Thus, consider an even stronger alternative—a lagged association that controls for prior levels of the outcome, as in Figure 13.3:

Lagged Association, Controlling for Prior Levels of the Outcome. T1 = Timepoint 1. T2 = Timepoint 2. From @Petersen2024a and @PetersenPrinciplesPsychAssessment.
Figure 13.3: Lagged Association, Controlling for Prior Levels of the Outcome. T1 = Timepoint 1. T2 = Timepoint 2. From Petersen (2024a) and Petersen (2024b).

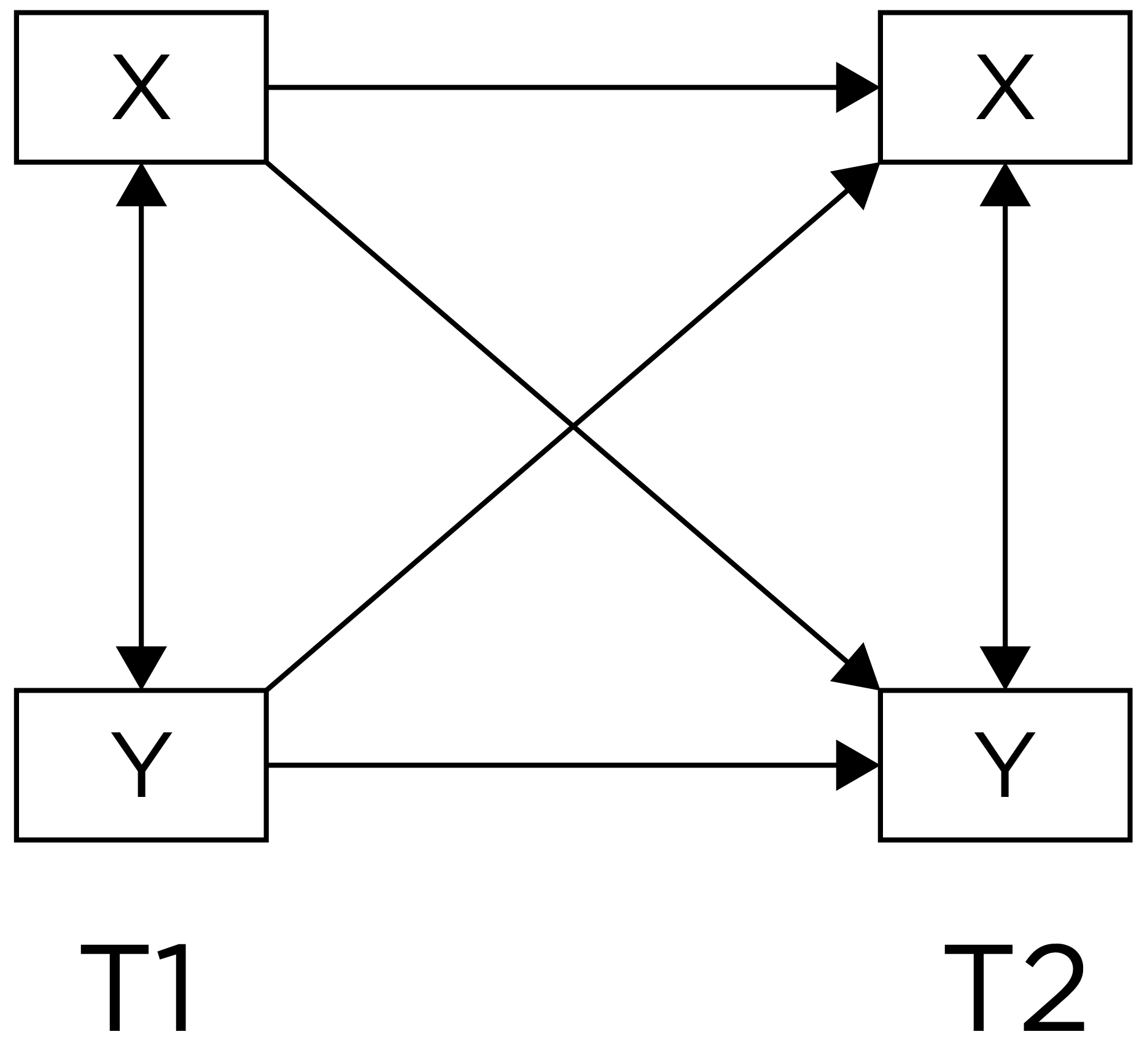
For instance, we might observe that sports drink performance before the game is associated with better player performance during the game, while controlling for prior player performance. A lagged association controlling for prior levels of the outcome has better internal validity than a lagged association that does not control for prior levels of the outcome. A lagged association that controls for prior levels further reduces the likelihood that the association owes to the reverse direction of effect, because earlier levels of the outcome are controlled. However, consider an even stronger alternative—lagged associations that control for prior levels of the outcome and that simultaneously test each direction of effect, as depicted in Figure 13.4:

Lagged Association, Controlling for Prior Levels of the Outcome, Simultaneously Testing Both Directions Of Effect. T1 = Timepoint 1. T2 = Timepoint 2. From @Petersen2024a and @PetersenPrinciplesPsychAssessment.
Figure 13.4: Lagged Association, Controlling for Prior Levels of the Outcome, Simultaneously Testing Both Directions Of Effect. T1 = Timepoint 1. T2 = Timepoint 2. From Petersen (2024a) and Petersen (2024b).

Lagged associations that control for prior levels of the outcome and that simultaneously test each direction of effect provide the strongest internal validity among observational/correlational designs. Such a design can help better clarify which among the variables is the chicken and the egg—which variable is more likely to be the cause and which is more likely to be the effect. If there are bidirectional effects, such a design can also help clarify the magnitude of each direction of effect. For instance, we can simultaneously evaluate the extent to which sports drink predicts later player performance (while controlling for prior performance) and the reverse—player performance predicting later sports drink consumption (while contorlling for prior sports drink consumption).

13.4.2.2 Within-Subject Analyses

Another design feature of longitudinal designs that can lead to greater internal validity is the use of within-subject analyses. Between-subject analyses, might examine, for instanc, whether players who consume more sports drink perform better on average compared to players who consume less sports drink. However, there are other between-person differences that could explain any observed between-subject associations between sports drink consumption and players performance. Another approach could be to apply within-subject analyses. For instance, you could examining whether, within the same individual, if a player consumes a sports drink, do they perform better compared to games in which they did not consume a sports drink. When we control for prior levels of the outcome in the prediction, we are evaluating whether the predictor is associated with witin-person change in the outcome. Predicting within-person change provides stronger evidence consistent with causality because it uses the individual as their own control and controls for many time-invariant confounds (i.e., confounds that do not change across time). However, predicting within-person change does not, by itself, control for time-varying confounds. So, it can also be useful to control for time-varying confounds, such as by use of control variables.

13.4.2.3 Control Variables

One of the plausible alternatives to the inference that X causes Y is that there are third variable confounds that influence both X and Y, thus explaining why X and Y are associated, as depicted in Figures 8.3 and 13.10. Thus, another approach that can help increase internal validity is to include plausible confounds as control variables. For instance, if a third variable such as education level might be a confound that influences both sports drink consumption and player performance, you could include education level as a covariate in the model. Inclusion of a covariate attempts to control for the variable by examining the association between the predictor variable and the outcome variable while holding the covariate variables constant. 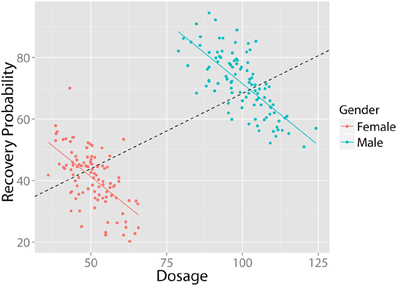For instance, such a model would examine whether, when accounting for education level, there is an association between sports drink consumption and player performance.

Failure to control for important third variables can lead to erroneous conclusions, as evidenced by the association depicted in Figure 13.5. In the example, if we did not control for gender, we would infer that there is a positive association between dosage and recovery probability. However, when we examine each men and women separately, we learn that the association between dosage and recovery probability is actually negative within each gender group. Thus, in this case, failure to control for gender would lead to false inferences about the association between dosage and recovery probability.

Example Where Failing to Control for a Variable (In This Case, Gender) Would Lead to False Inferences. In this example, the association between dosage and recovery probability is positive at the population level, but the association is negative among men and women separately. (Figure reprinted from @Kievit2013, Figure 1, p. 2. Kievit, R., Frankenhuis, W., Waldorp, L., & Borsboom, D. (2013). Simpson's paradox in psychological science: A practical guide. *Frontiers in Psychology*, *4*(513). https://doi.org/10.3389/fpsyg.2013.00513)
Figure 13.5: Example Where Failing to Control for a Variable (In This Case, Gender) Would Lead to False Inferences. In this example, the association between dosage and recovery probability is positive at the population level, but the association is negative among men and women separately. (Figure reprinted from Kievit et al. (2013), Figure 1, p. 2. Kievit, R., Frankenhuis, W., Waldorp, L., & Borsboom, D. (2013). Simpson’s paradox in psychological science: A practical guide. Frontiers in Psychology, 4(513). https://doi.org/10.3389/fpsyg.2013.00513)

However, it can be problematic to control for variables indiscriminantly (Spector & Brannick, 2010; Wysocki et al., 2022). The use of causal diagrams can inform which variables are important to be included as control variables, and—just as important—which variables not to include as control variables, as described in Section 13.5.

13.4.2.4 Genetically Informed Designs

Another approach to control for variables is to use genetically informed designs. Genetically informed designs allow controlling for potential genetic effects in order to more closely approximate the contributions of various environmental effects. Genetically informed designs exploit differing degrees of genetic relatedness among participants to capture the extent to which genetic factors may contribute to an outcome. The average percent of DNA shared between people of varying relationships is provided in Table 13.1 (https://isogg.org/wiki/Autosomal_DNA_statistics; archived at https://perma.cc/MK3D-DST8):

Table 13.1: Average Percent of Autosomal DNA Shared by Pairs of Relatives by Relationship Type.
Relationship Average Percent of Autosomal DNA Shared by Pairs of Relatives
Monozygotic (“identical”) twins 100%
Dizygotic (“fraternal”) twins 50%
Parent/child 50%
Full siblings 50%
Grandparent/grandchild 25%
Aunt-or-uncle/niece-or-nephew 25%
Half-siblings 25%
First cousin 12.5%
Great-grandparent/great-grandchild 12.5%

For instance, researchers may compare monozygotic twins versus dizygotic twins in some outcome—a so-called “twin study”. It is assumed that the trait/outcome is attributable to genetic factors to the extent that the monozygotic twins (who share 100% of their DNA) are more similar in the trait or outcome compared to the dizygotic twins (who share on average 50% of their DNA). Alternatively, researchers could compare full siblings versus half-siblings, or they could compare full siblings versus first cousins.

Genetically informed designs are not as relevant for fantasy football analytics, but they are useful to present as one of various design features that researchers can draw upon to strengthen their ability to make causal inferences.

13.5 Causal Diagrams

13.5.1 Overview

A key tool when describing a research question or hypothesis is to create a conceptual depiction of the hypothesized causal processes. A causal diagram depicts the hypothesized causal processes that link two or more variables. A common form of causal diagrams is the directed acyclic graph (DAG). DAGs provide a helpful tool to communicate about causal questions and help identify how to avoid bias (i.e., overestimation) in associations between variables due to confounding (i.e., common causes) (Digitale et al., 2022). For instance, from a DAG, it is possible to determine what variables it is important to control for in order to get unbiased estimates of the association between two variables of interest. To create DAGs, you can use the R package dagitty (Textor et al., 2017) or the associated browser-based extension, DAGitty: https://dagitty.net (archived at https://perma.cc/U9BY-VZE2). Examples of various causal diagrams that could explain why X is associated with Y are in Figures 13.6, 13.8 and 13.10.

Code
XCausesY <- dagitty::dagitty("dag{
  X -> Y
}")

plot(dagitty::graphLayout(XCausesY))

dagitty::impliedConditionalIndependencies(XCausesY)
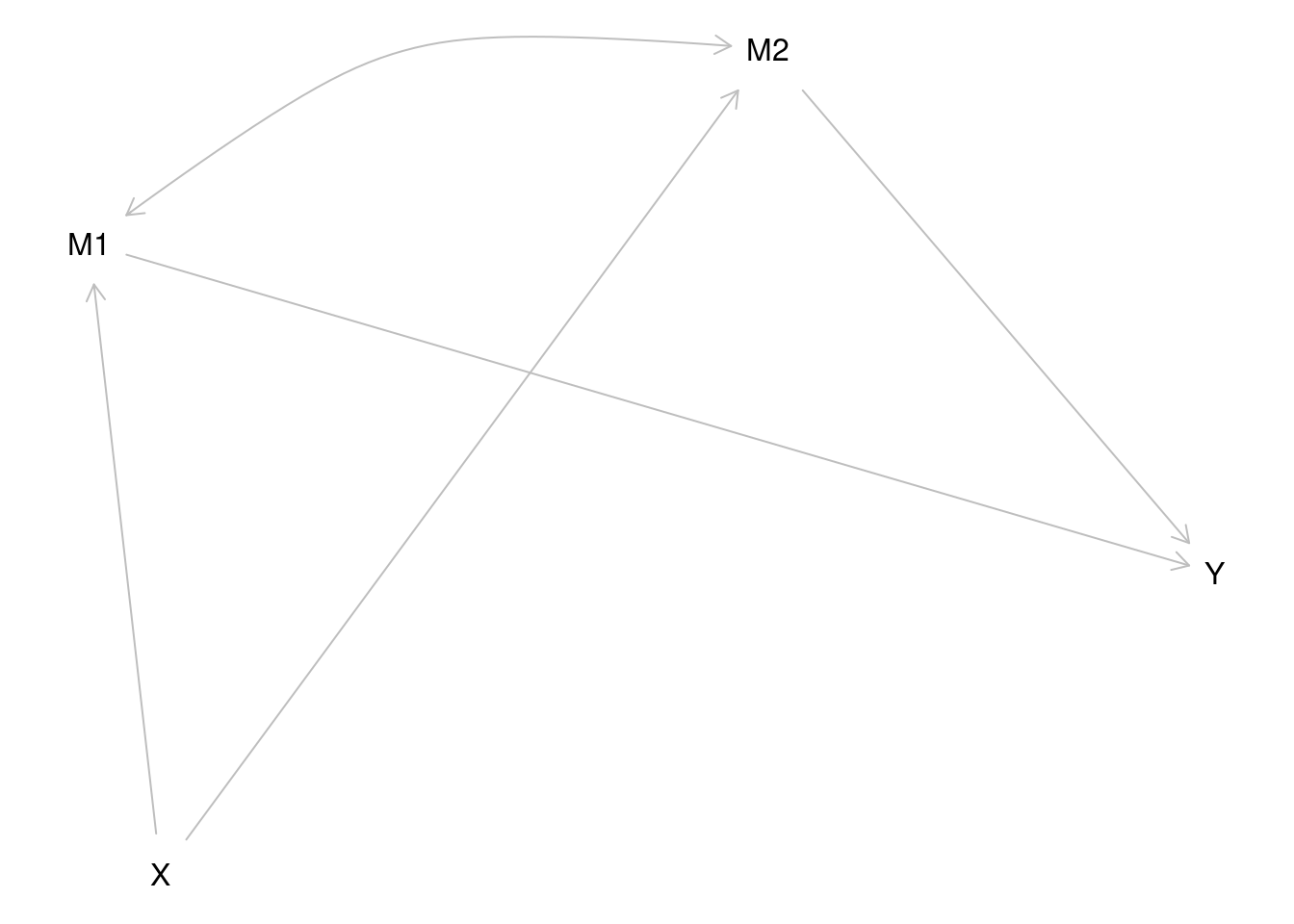
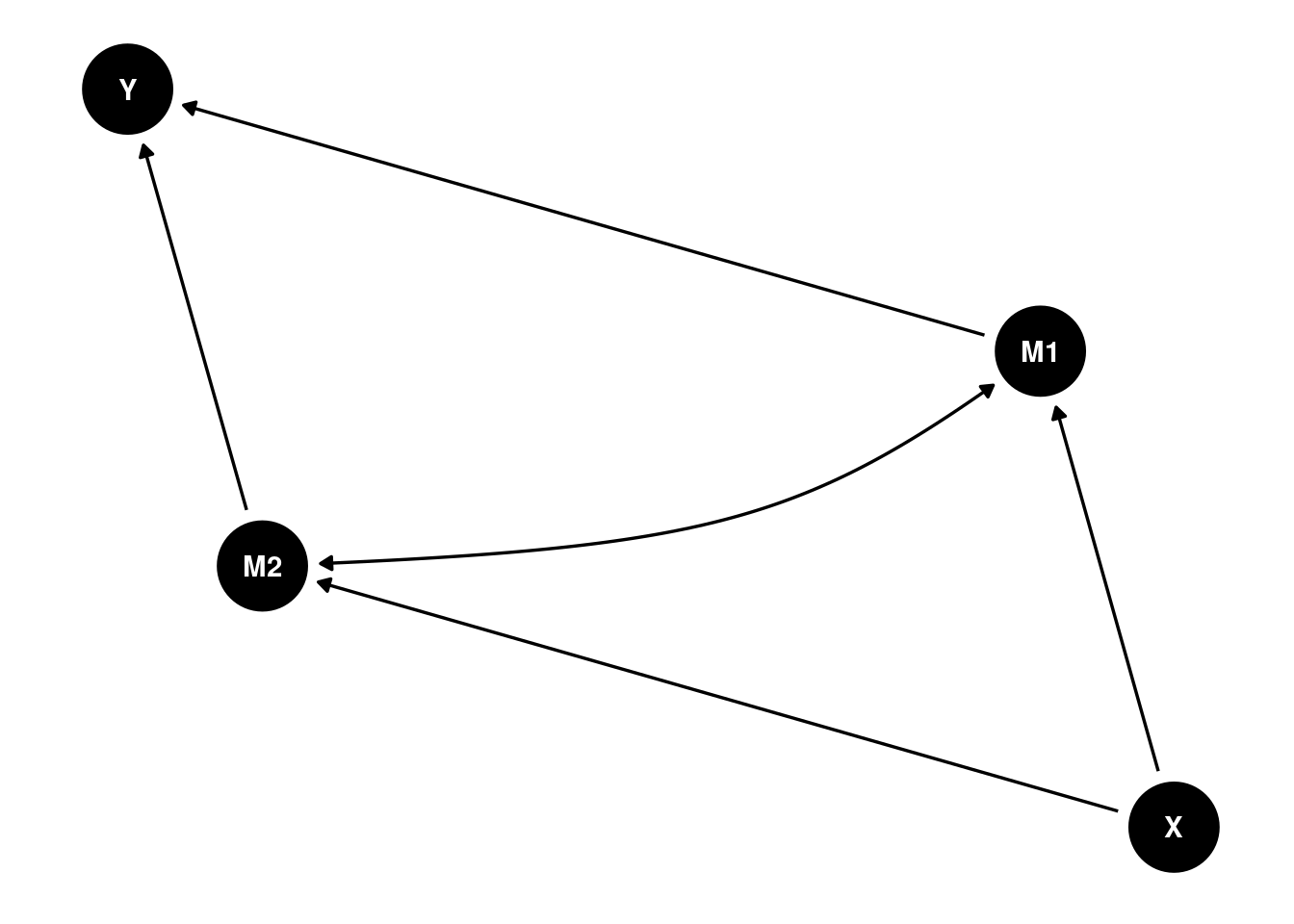
Causal Diagram (Directed Acyclic Graph) Depicting `X` Causing `Y`.
Figure 13.6: Causal Diagram (Directed Acyclic Graph) Depicting X Causing Y.

Here is an alternative way of specifying the same diagram (more similar to lavaan syntax):

Code
XCausesY_alt <- ggdag::dagify(
  Y ~ X
)

#plot(XCausesY_alt) # this creates the same plot as above
ggdag::ggdag(XCausesY_alt) + theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Depicting `X` Causing `Y`.
Figure 13.7: Causal Diagram (Directed Acyclic Graph) Depicting X Causing Y.
Code
YCausesX <- dagitty::dagitty("dag{
  Y -> X
}")

plot(dagitty::graphLayout(YCausesX))

dagitty::impliedConditionalIndependencies(YCausesX)
Causal Diagram (Directed Acyclic Graph) Depicting Reverse Causation: `Y` Causing `X`.
Figure 13.8: Causal Diagram (Directed Acyclic Graph) Depicting Reverse Causation: Y Causing X.

Here is an alternative way of specifying the same diagram (more similar to lavaan syntax):

Code
YCausesX_alt <- ggdag::dagify(
  X ~ Y
)

#plot(YCausesX_alt) # this creates the same plot as above
ggdag::ggdag(YCausesX_alt) + theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Depicting Reverse Causation: `Y` Causing `X`.
Figure 13.9: Causal Diagram (Directed Acyclic Graph) Depicting Reverse Causation: Y Causing X.
Code
ZCausesXandY <- dagitty::dagitty("dag{
  Z -> Y
  Z -> X
  X <-> Y
}")

plot(dagitty::graphLayout(ZCausesXandY))
Causal Diagram (Directed Acyclic Graph) Depicting a Third Variable Confound, `Z`, Causing `X` and `Y`, Thus Explaining Why `X` and `Y` are associated.
Figure 13.10: Causal Diagram (Directed Acyclic Graph) Depicting a Third Variable Confound, Z, Causing X and Y, Thus Explaining Why X and Y are associated.

Here is an alternative way of specifying the same diagram (more similar to lavaan syntax):

Code
ZCausesXandY_alt <- ggdag::dagify(
  X ~ Z,
  Y ~ Z,
  X ~~ Y
)

#plot(ZCausesXandY_alt) # this creates the same plot as above
ggdag::ggdag(ZCausesXandY_alt) + theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Depicting a Third Variable Confound, `Z`, Causing `X` and `Y`, Thus Explaining Why `X` and `Y` are associated.
Figure 13.11: Causal Diagram (Directed Acyclic Graph) Depicting a Third Variable Confound, Z, Causing X and Y, Thus Explaining Why X and Y are associated.

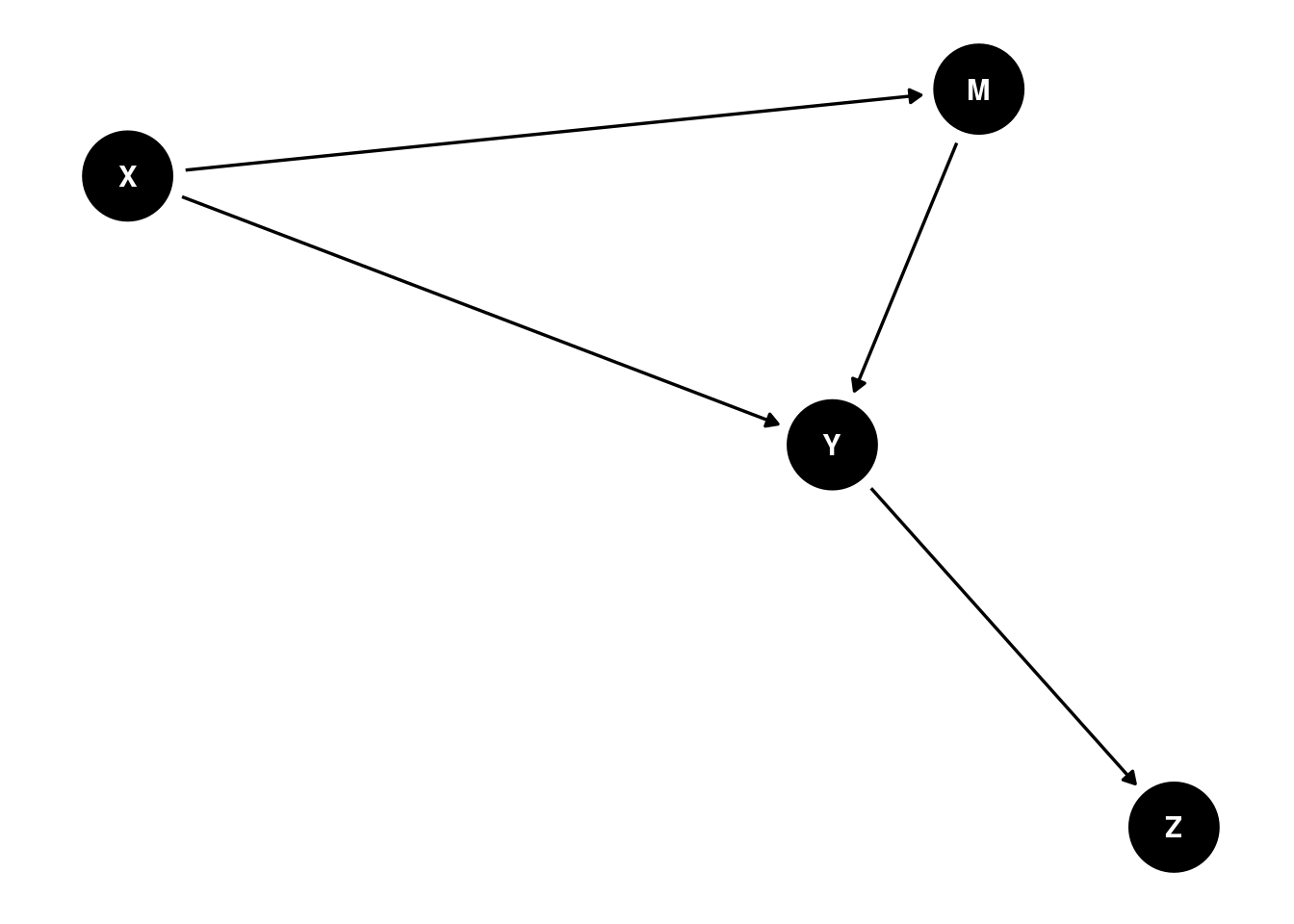
Consider another example in Figure 13.12:

Code
mediationDag <- dagitty::dagitty("dag{
  X -> M1
  X -> M2
  M1 -> Y
  M2 -> Y
  M1 <-> M2
}")

plot(dagitty::graphLayout(mediationDag))
Causal Diagram (Directed Acyclic Graph).
Figure 13.12: Causal Diagram (Directed Acyclic Graph).
Code
dagitty::impliedConditionalIndependencies(mediationDag)
X _||_ Y | M1, M2
Code
dagitty::adjustmentSets(
  mediationDag, 
  exposure = "M1",
  outcome = "Y",
  effect = "total")
{ M2 }

In this example, X influences Y via M1 and M2 (i.e., multiple mediators), and M1 is also associated with M2. The dagitty::impliedConditionalIndependencies() function identifies variables in the causal diagram that are conditionally independent (i.e., uncorrelated) after controlling for other variables in the model. For this causal diagram, X is conditionally independent with Y because X is independent with Y when controlling for M1 and M2.

The dagitty::adjustmentSets() function identifies variables that would be necessary to control for (i.e., to include as covariates) in order to identify an unbiased estimate of the association (whether the total effect, i.e., effect = "total"; or the direct effect, i.e., effect = "direct") between two variables (exposure and outcome). In this case, to identify the unbiased association between M1 and Y, it is important to control for M2.

Here is an alternative way of specifying the same diagram (more similar to lavaan syntax):

Code
mediationDag_alt <- ggdag::dagify(
  M1 ~ X,
  M2 ~ X,
  Y ~ M1,
  Y ~ M2,
  M1 ~~ M2
)

#plot(mediationDag_alt) # this creates the same plot as above
ggdag::ggdag(mediationDag_alt) + theme_dag_blank()
Causal Diagram (Directed Acyclic Graph).
Figure 13.13: Causal Diagram (Directed Acyclic Graph).

13.5.2 Confounding

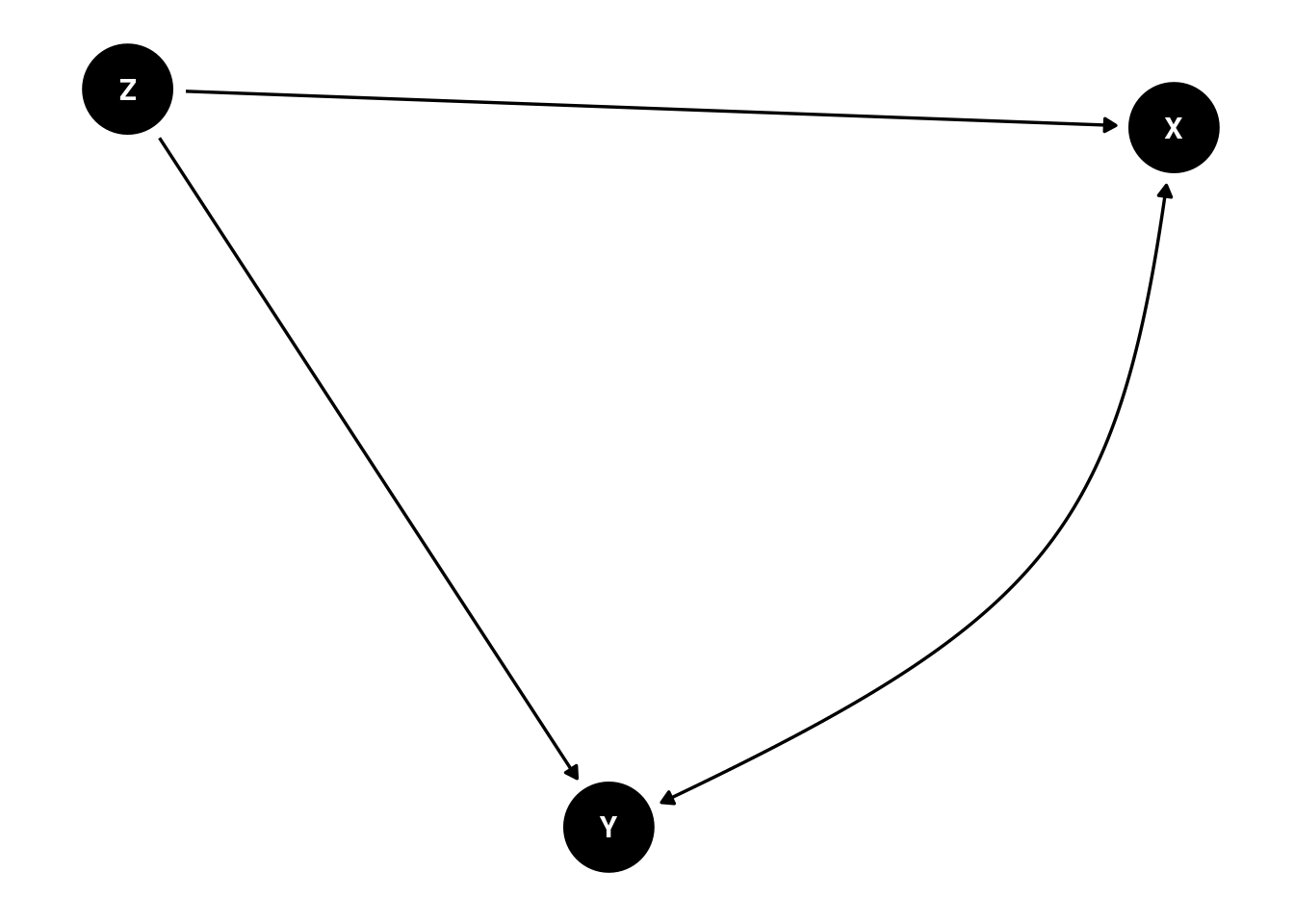
Confounding occurs when two variables—that are both caused by another variable(s)—have a spurious or noncausal association (D’Onofrio et al., 2020). That is, two variables share a common cause, and the common cause leads the variables to be associated even though they are not causally related. The common cause—i.e., the variable that influences the two variables—is known as a confound (or confounder). 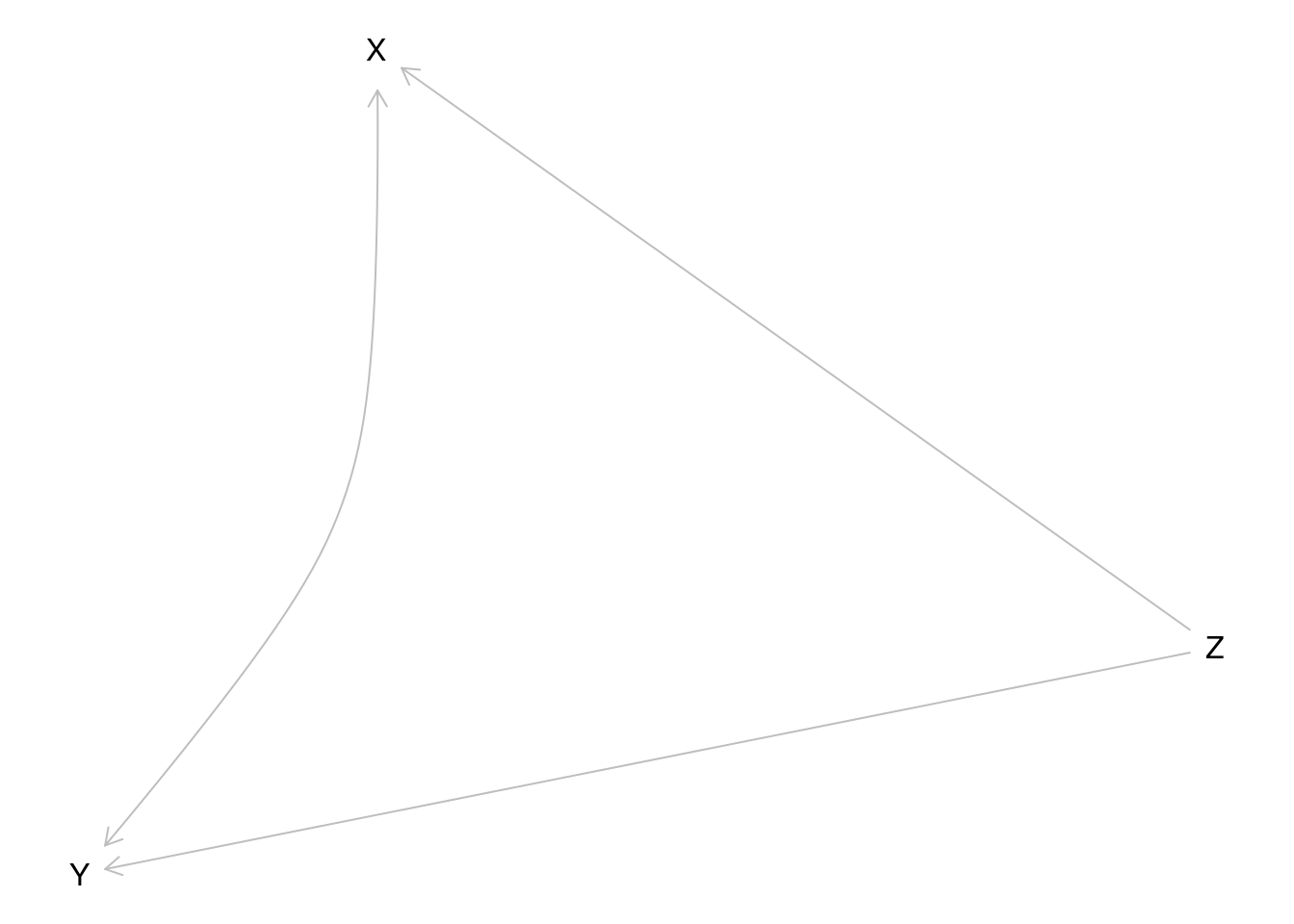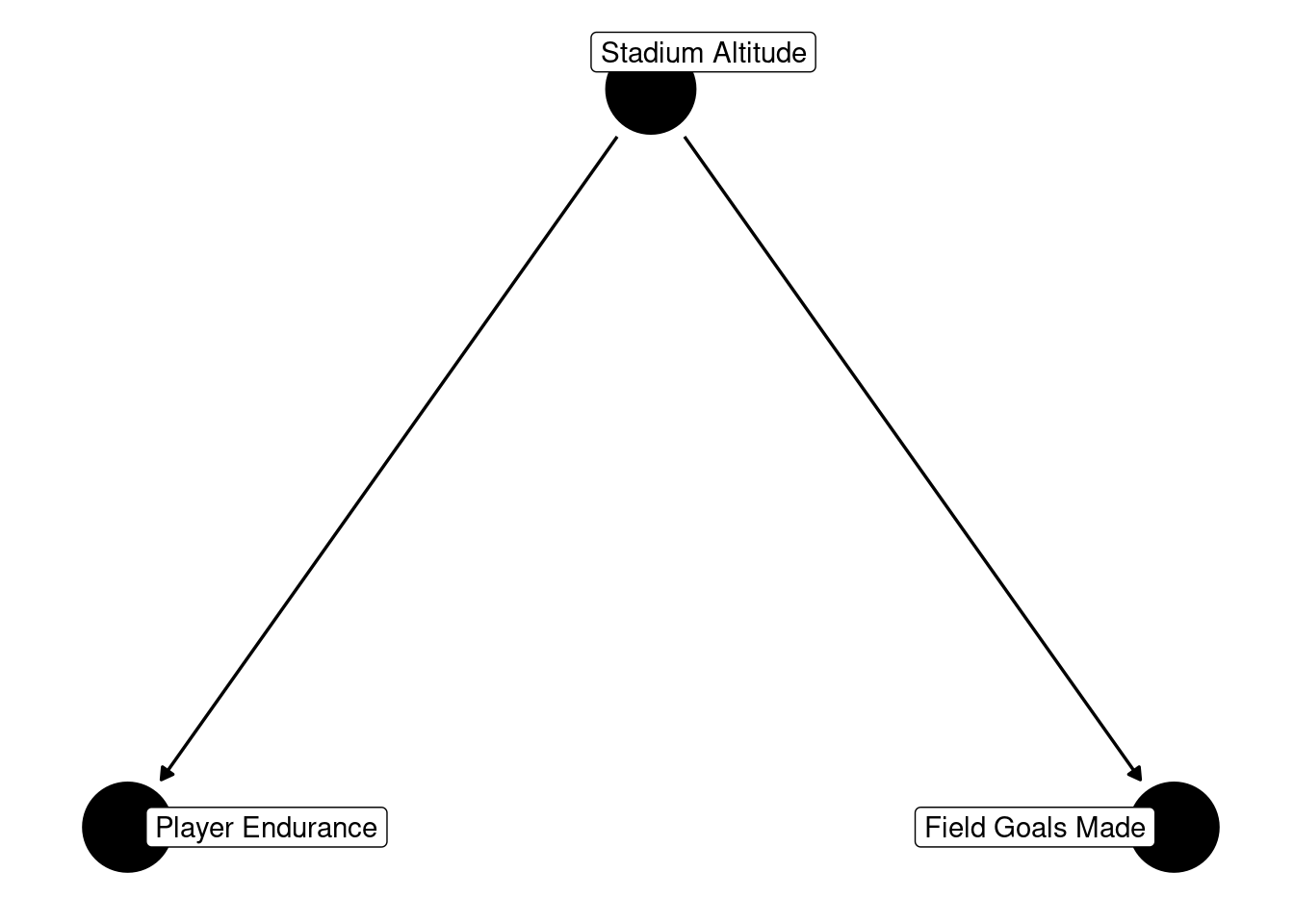An example of confounding is depicted in Figure 13.14:

Code
confounding <- ggdag::confounder_triangle(
  x = "Player Endurance",
  y = "Field Goals Made",
  z = "Stadium Altitude") 

confounding %>%
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Confounding.
Figure 13.14: Causal Diagram (Directed Acyclic Graph) Example of Confounding.
Code
dagitty::impliedConditionalIndependencies(confounding)
x _||_ y | z

The output indicates that player endurance (X) and field goals made (Y) are conditionally independent when accounting for stadium altitude (Z). Conditional independence refers to two variables being unassociated when controlling for other variables.

Code
dagitty::adjustmentSets(
  confounding, 
  exposure = "x",
  outcome = "y",
  effect = "total")
{ z }

The output indicates that, to obtain an unbiased estimate of the causal association between two variables, it is necessary to control for any confounding (Lederer et al., 2019). That is, to obtain an unbiased estimate of the causal association between player endurance (X) and field goals made (Y), it is necessary to control for stadium altitude (Z).

13.5.3 Mediation

Mediation can be divided into two types: full and partial. In full mediation, the mediator(s) fully account for the effect of the predictor variable on the outcome variable. In partial mediation, the mediator(s) partially but do not fully account for the effect of the predictor variable on the outcome variable.

13.5.3.1 Full Mediation

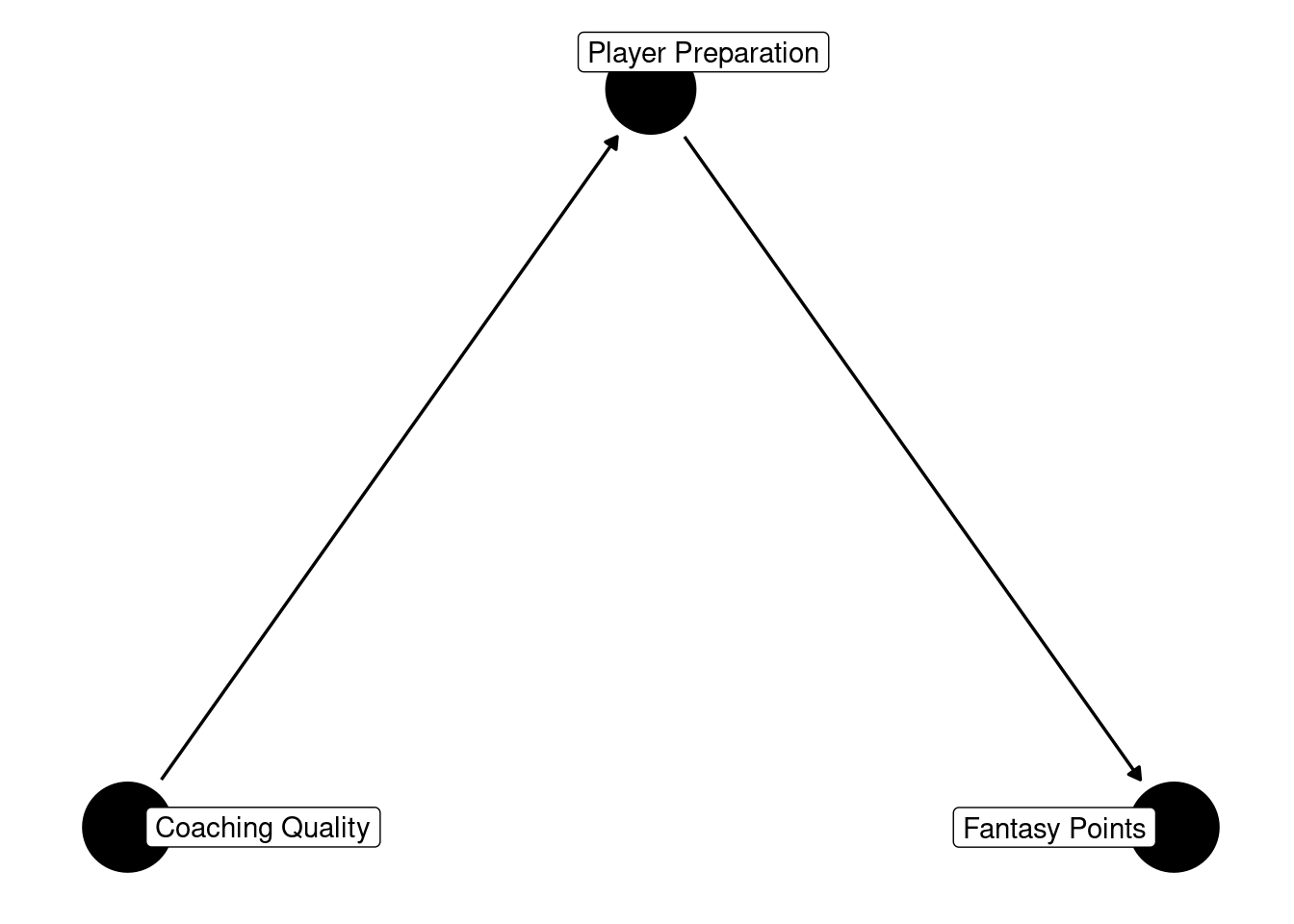
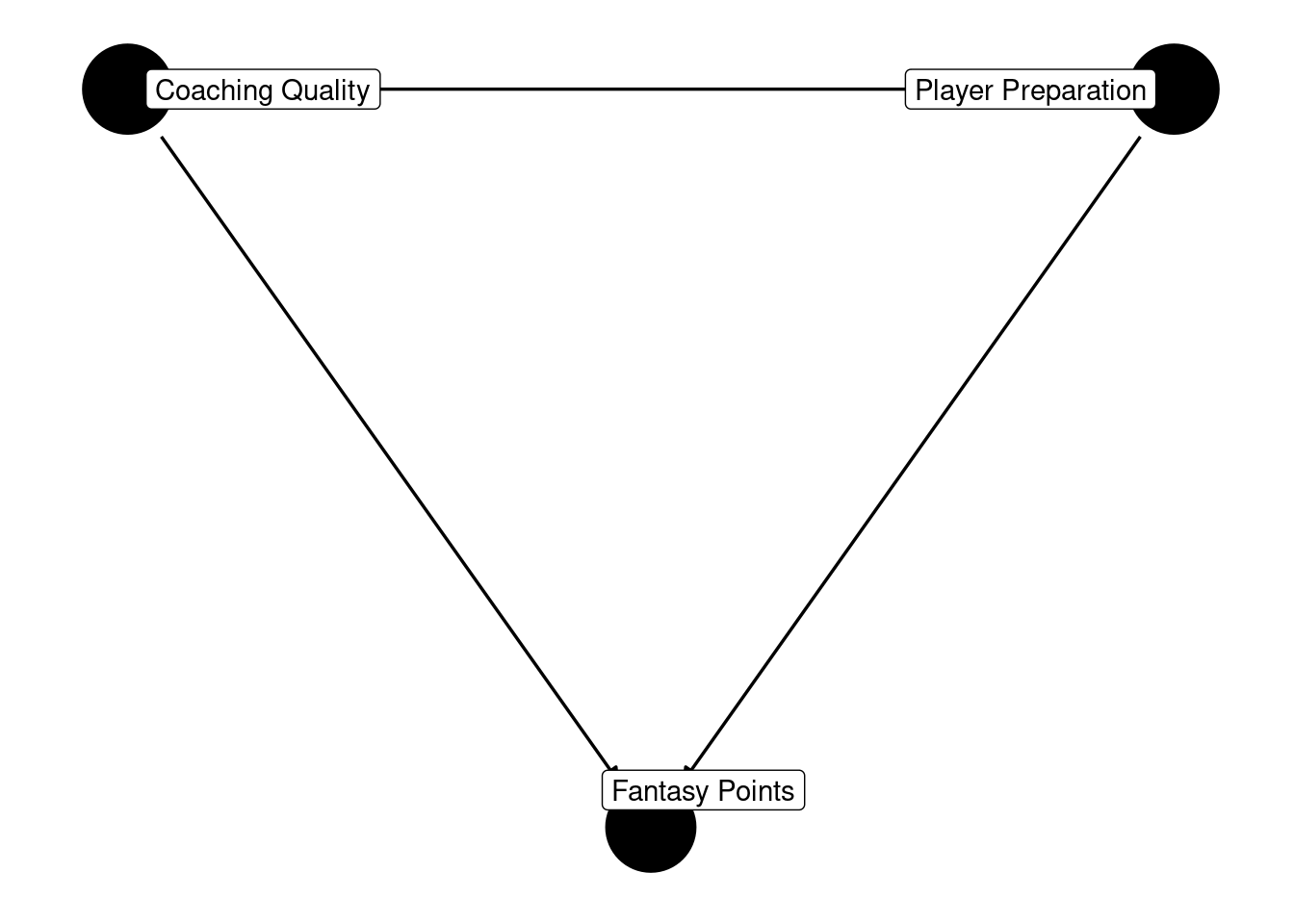
An example of full mediation is depicted in Figure 13.15:

Code
full_mediation <- ggdag::mediation_triangle(
  x = "Coaching Quality",
  y = "Fantasy Points",
  m = "Player Preparation")

full_mediation %>%
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Full Mediation.
Figure 13.15: Causal Diagram (Directed Acyclic Graph) Example of Full Mediation.
Code
dagitty::impliedConditionalIndependencies(full_mediation)
x _||_ y | m

In full mediation, X and Y are conditionally independent when accounting for the mediator (Z). In this case, coaching quality (X) and fantasy points (Y) are conditionally independent when accounting for player preparation (M). In other words, in this example, player preparation is the mechanism that fully (i.e., 100%) accounts for the effect of coaching quality on players’ fantasy points.

Code
dagitty::adjustmentSets(
  full_mediation, 
  exposure = "x",
  outcome = "y",
  effect = "direct")
{ m }

The output indicates that, to obtain an unbiased estimate of the direct causal association between coaching quality (X) and fantasy points (Y) (i.e., the effect that is not mediated through intermediate processes), it is necessary to control for player preparation (M).

Code
dagitty::adjustmentSets(
  full_mediation, 
  exposure = "x",
  outcome = "y",
  effect = "total")
 {}

However, to obtain an unbiased estimate of the total causal association between coaching quality (X) and fantasy points (Y) (i.e., including the portion of the effect that is mediated through intermediate processes), it is important not to control for player preparation (M). When the goal is to understand the (total) causal effect of coaching quality (X) and fantasy points (Y), controlling for the mediator (player preparation; M) would be inappropriate because doing so would remove the causal effect, thus artificially reducing the estimate of the association between coaching quality (X) and fantasy points (Y) (Lederer et al., 2019).

13.5.3.2 Partial Mediation

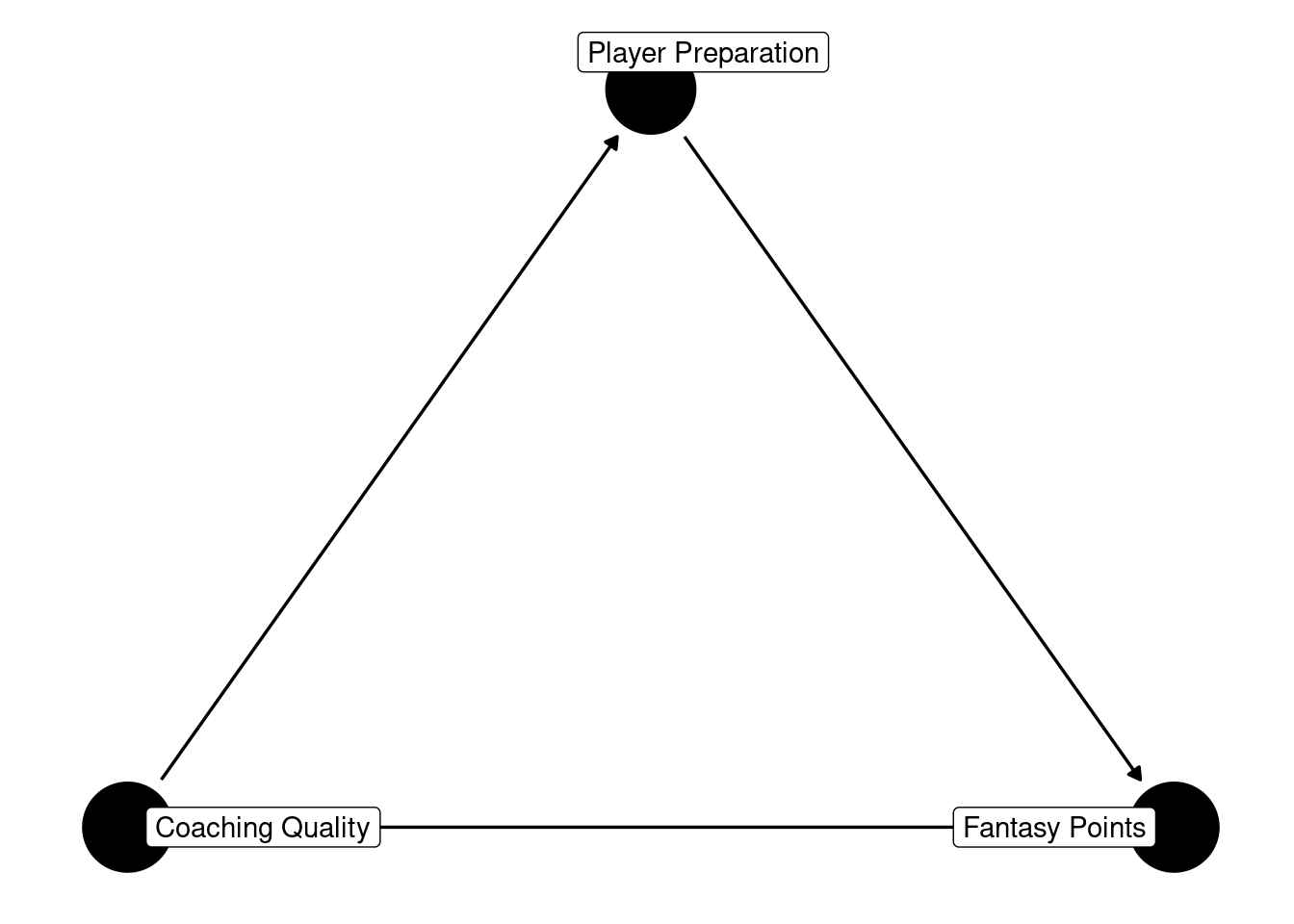
An example of partial mediation is depicted in Figure 13.16:

Code
partial_mediation <- ggdag::mediation_triangle(
  x = "Coaching Quality",
  y = "Fantasy Points",
  m = "Player Preparation",
  x_y_associated = TRUE)

partial_mediation %>%
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Partial Mediation.
Figure 13.16: Causal Diagram (Directed Acyclic Graph) Example of Partial Mediation.
Code
dagitty::impliedConditionalIndependencies(partial_mediation)

In partial mediation, X and Y are not conditionally independent when accounting for the mediator (Z). In this case, coaching quality (X) and fantasy points (Y) are still associated when accounting for player preparation (M). In other words, in this example, player preparation is a mechanism that partially but does not fully account for the effect of coaching quality on players’ fantasy points. That is, there are likely other mechanisms, in addition to player preparation, that collectively account for the effect of coaching quality on fantasy points. For instance, coaching quality could also influence player fantasy points through better play-calling.

Code
dagitty::adjustmentSets(
  partial_mediation, 
  exposure = "x",
  outcome = "y",
  effect = "direct")
{ m }

As with full mediation, the output indicates that, to obtain an unbiased estimate of the direct causal association between coaching quality (X) and fantasy points (Y) (i.e., the effect that is not mediated through intermediate processes), it is necessary to control for player preparation (M).

Code
dagitty::adjustmentSets(
  partial_mediation, 
  exposure = "x",
  outcome = "y",
  effect = "total")
 {}

However, as with full mediation, to obtain an unbiased estimate of the total causal association between coaching quality (X) and fantasy points (Y) (i.e., including the portion of the effect that is mediated through intermediate processes), it is important not to control for player preparation (M). When the goal is to understand the (total) causal effect of coaching quality (X) and fantasy points (Y), controlling for a mediator (player preparation; M) would be inappropriate because doing so would remove the causal effect, thus artificially reducing the estimate of the association between coaching quality (X) and fantasy points (Y) (Lederer et al., 2019).

13.5.4 Ancestors and Descendants

In a causal model, an ancestor is a variable that influences another variable, either directly or indirectly via another variable (Rohrer, 2018). A descendant is a variable that is influenced by another variable (Rohrer, 2018). In general, one should not control for descendants of the outcome variable, because doing so could eliminate the apparent effect of a legitimate cause on the outcome variable (Digitale et al., 2022). Moreover, as described above, when trying to understand the total causal effect of a predictor variable on an outcome variable, one should not control for descendants of the predictor variable that are also antecedents of the outcome variable (i.e., mediators of the effect of the predictor variable on the outcome variable) (Digitale et al., 2022).

Consider the example in Figure 13.17:

Code
descendentDag <- dagitty::dagitty("dag{
  X -> M
  M -> Y
  X -> Y
  Y -> Z
}")

#plot(dagitty::graphLayout(descendentDag))
ggdag::ggdag(descendentDag) + theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Ancestor (Mediation) and Descendant of Y.
Figure 13.17: Causal Diagram (Directed Acyclic Graph) Example of Ancestor (Mediation) and Descendant of Y.
Code
dagitty::impliedConditionalIndependencies(descendentDag)
M _||_ Z | Y
X _||_ Z | Y

In this example, X and M are conditionally independent with Z when accounting for the mediator (Y).

Code
dagitty::adjustmentSets(
  descendentDag, 
  exposure = "X",
  outcome = "Y",
  effect = "direct")
{ M }
Code
dagitty::adjustmentSets(
  descendentDag, 
  exposure = "X",
  outcome = "Y",
  effect = "total")
 {}

As indicated above, one should not control for the descendant of the outcome variable; thus, one should not control for Z when examining the association between X or M and Y.

13.5.5 Collider Bias

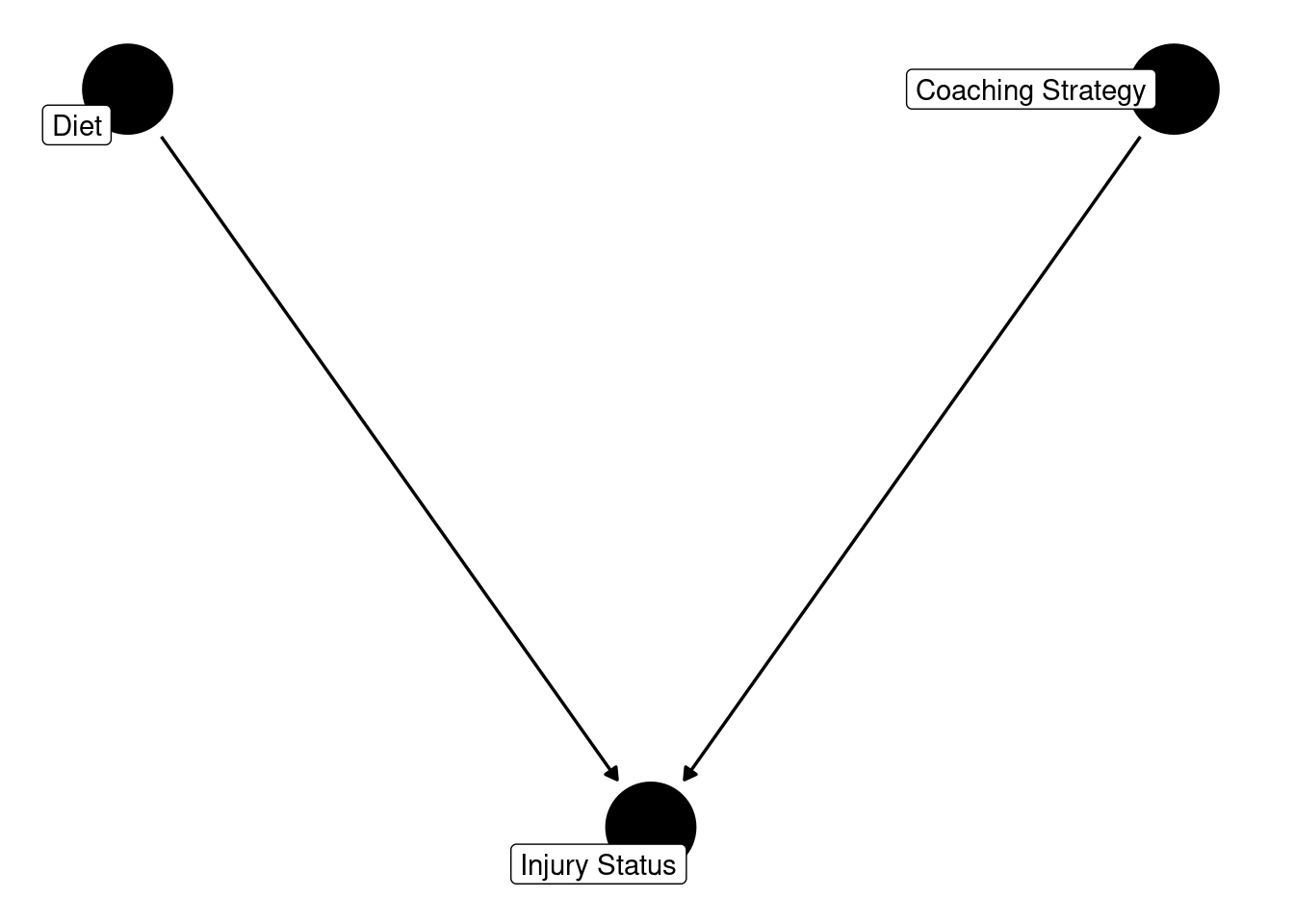
Collision occurs when two variables influence a third variable, the collider (D’Onofrio et al., 2020). That is, a collider is a variable that is caused by two other variables (i.e., a common effect). An example collision is depicted in Figures 13.18 and 13.19:

Code
colliderBias1 <- ggdag::collider_triangle(
  x = "Diet",
  y = "Coaching Strategy",
  m = "Injury Status")

colliderBias1 %>% 
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of a Collision with a Collider (Injury Status).
Figure 13.18: Causal Diagram (Directed Acyclic Graph) Example of a Collision with a Collider (Injury Status).
Code
dagitty::impliedConditionalIndependencies(colliderBias1)
x _||_ y

In this example collision, diet (X) and coaching strategy (Y) are independent.

Code
dagitty::adjustmentSets(
  colliderBias1, 
  exposure = "x",
  outcome = "y",
  effect = "total")
 {}

As the output indicates, we should not control for the collider when examining the association between the two causes of the collider. That is, we should not control for injury status (M) when examining the association between diet (X) and coaching strategy. Controlling for the collider leads to confounding and can artificially induce an association between the two causes of the collider despite no causal association between them (Lederer et al., 2019). Obtaining a distorted or artificial association between two variables due to inappropriately controlling for a collider is known as collider bias.

Consider another example:

Code
colliderBias2 <- ggdag::collider_triangle(
  x = "Coaching Quality",
  y = "Player Preparation",
  m = "Fantasy Points",
  x_y_associated = TRUE)

colliderBias2 %>% 
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Collider Bias.
Figure 13.19: Causal Diagram (Directed Acyclic Graph) Example of Collider Bias.
Code
dagitty::impliedConditionalIndependencies(colliderBias2)

In this example of collider bias, there are no conditional independencies.

Code
dagitty::adjustmentSets(
  colliderBias2, 
  exposure = "x",
  outcome = "y",
  effect = "total")
 {}

Again, it would be important not to control for the collider, fantasy points (M), when examining the association between coaching quality (X) and player preparation (Y). In this case, controlling for the collider would remove some of the causal effect of coaching quality on player preparation and could lead to an artificially smaller estimate of the causal effect between coaching quality and player preparation.

13.5.5.1 M-Bias

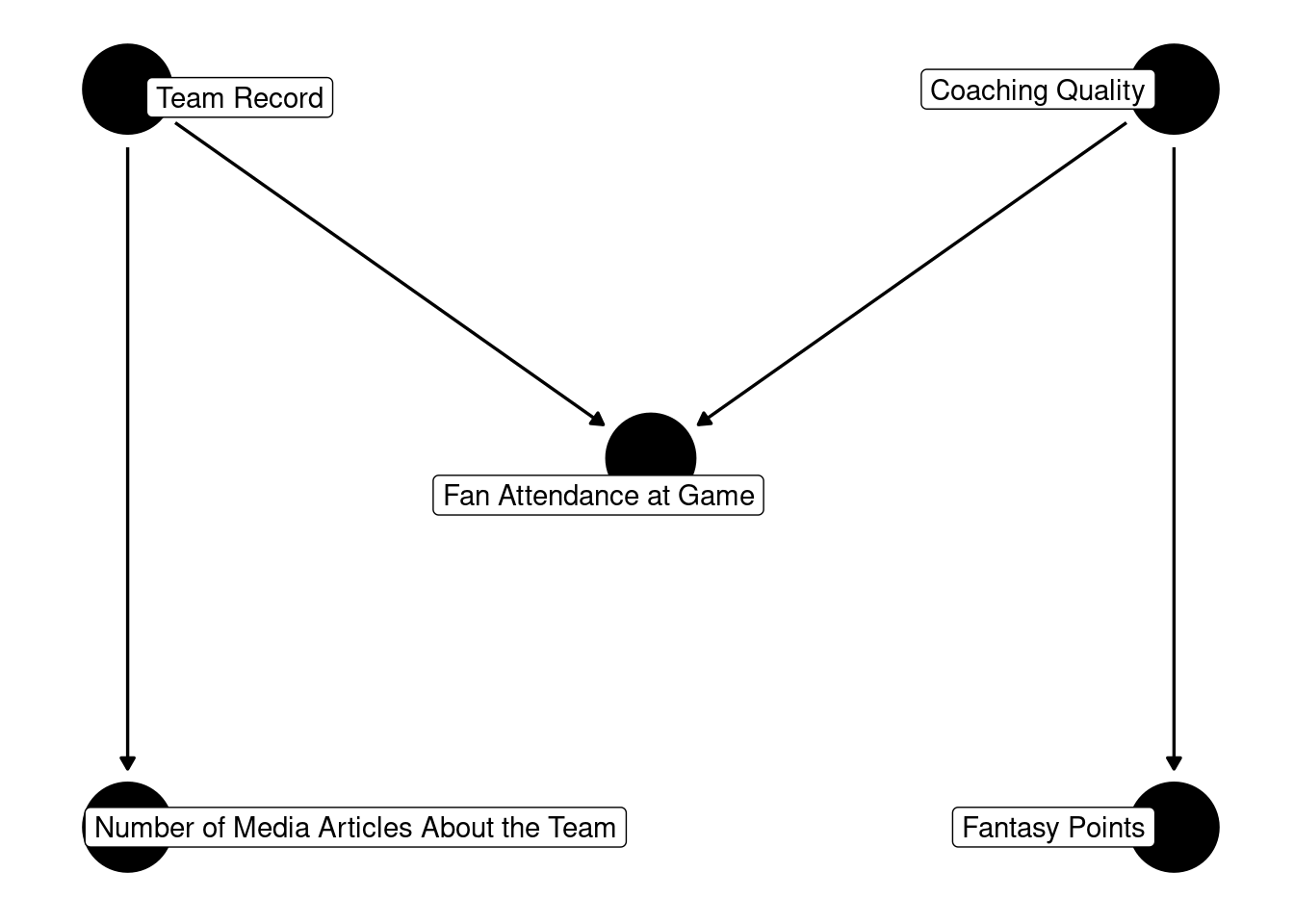
Collider bias may also occur when neither variable of interest is a direct cause of the collider (Lederer et al., 2019). M-bias is a form of collider bias that occurs when two variables that are not causally related, A and B, both influence a collider, M, and each (A and B) also influences a separate variable—e.g., A influences X and B influences Y. M-bias is so-named from the M-shape of the DAG. An example of M-bias is depicted in Figure 13.20:

Code
mBias <- ggdag::m_bias(
  x = "Number of Media Articles About the Team",
  y = "Fantasy Points",
  a = "Team Record",
  b = "Coaching Quality",
  m = "Fan Attendance at Game")

mBias %>% 
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of M-Bias.
Figure 13.20: Causal Diagram (Directed Acyclic Graph) Example of M-Bias.

In this example, fan attendance is the collider that is influenced separately by the team record and the coaching quality. This is a fictitious example for purposes of demonstration; in reality, coaching quality influences the team’s record.

Code
dagitty::impliedConditionalIndependencies(mBias)
a _||_ b
a _||_ y
b _||_ x
m _||_ x | a
m _||_ y | b
x _||_ y

As the output indicates, there are several conditional independencies.

Code
dagitty::adjustmentSets(
  mBias, 
  exposure = "x",
  outcome = "y",
  effect = "total")
 {}

It is important not to control for the collider (fan attendance). If you control for the collider, you can induce an artificial association between team record and coaching quality. Moreover, because doing so induces an artificial association between team record and coaching quality, it can also induce an artificial association between the effects of team record and coaching quality: number of media articles about the team and fantasy points, respectively. That is, controlling for the collider can lead to an artificial association between X and Y that does not reflect a causal process.

13.5.5.2 Butterfly Bias

Butterfly bias occurs when both confounding and M-bias are present. Butterfly bias (aka bow-tie bias) is so-named from the butterfly shape of the DAG. In butterfly bias, the following criteria are met:

  • Two variables (A and B) influence a collider (M).
  • The collider influences two variables, X and Y.
  • A also influences X.
  • B also influences Y.
  • A and B are not causally related.
  • X and Y are not causally related.

Or, more succinctly:

  • A influences M and X.
  • B influences M and Y.
  • M influences X and Y.

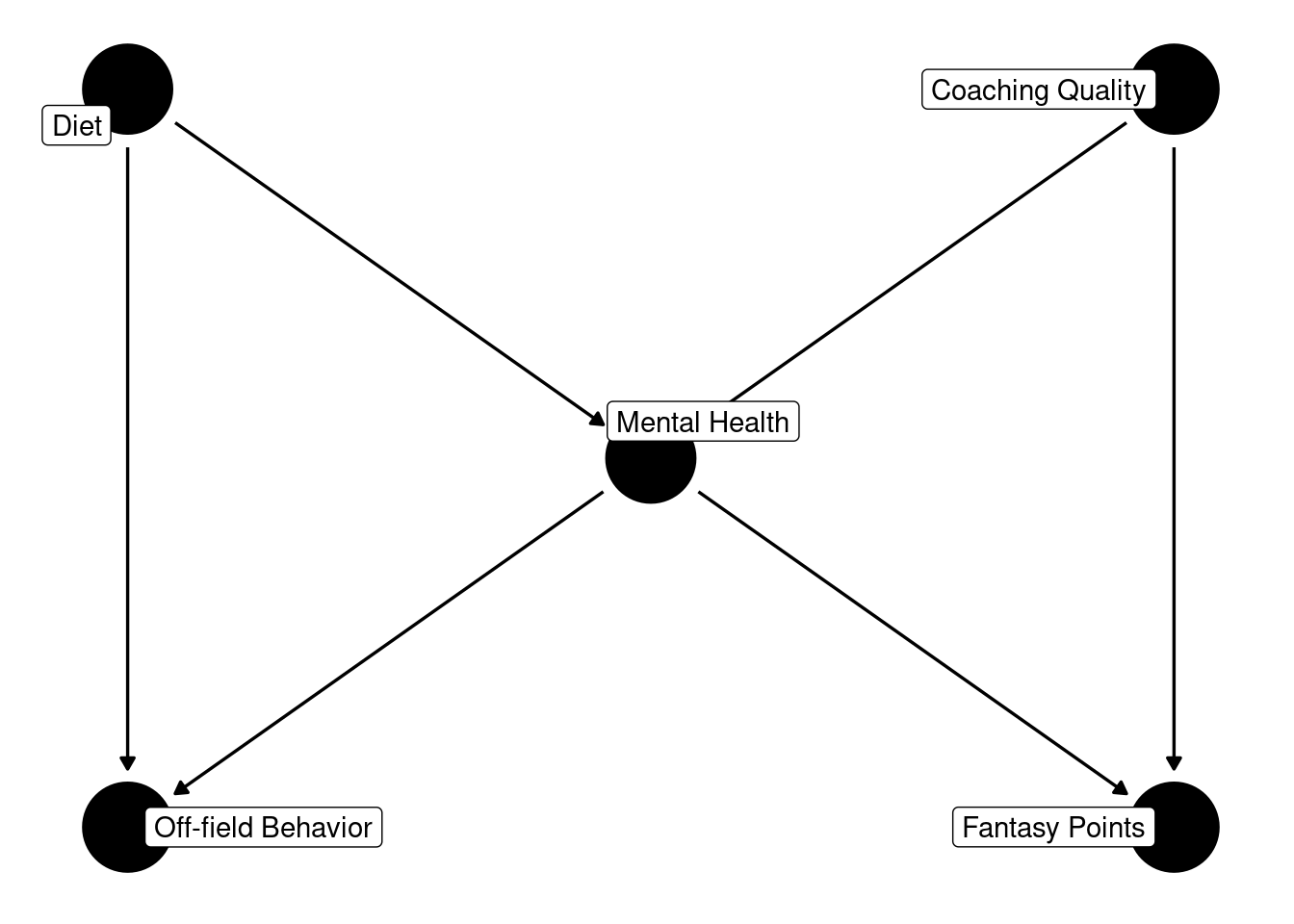
In butterfly bias, the collider (M) is also a confound. That is, a variable is both influenced by two variables and influences two variables. An example of butterfly bias is depicted in Figure 13.21:

Code
butterflyBias <- ggdag::butterfly_bias(
  x = "Off-field Behavior",
  y = "Fantasy Points",
  a = "Diet",
  b = "Coaching Quality",
  m = "Mental Health")

butterflyBias %>% 
  ggdag(
    text = FALSE,
    use_labels = "label") + 
  theme_dag_blank()
Causal Diagram (Directed Acyclic Graph) Example of Butterfly Bias.
Figure 13.21: Causal Diagram (Directed Acyclic Graph) Example of Butterfly Bias.

In this case, players’ mental health is a collider of their diet and the quality of the coaching they receive. In addition, players’ mental health is a confound of their off-field behavior and fantasy points.

Code
dagitty::impliedConditionalIndependencies(butterflyBias)
a _||_ b
a _||_ y | b, m
b _||_ x | a, m
x _||_ y | b, m
x _||_ y | a, m

As the output indicates, there are several conditional independencies.

Code
dagitty::adjustmentSets(
  butterflyBias, 
  exposure = "x",
  outcome = "y",
  effect = "total")
{ b, m }
{ a, m }

When dealing with a collider that is also a confound, controlling for either set, B and M or A and M, will provide an unbiased estimate of the association between X and Y. In this case, controlling for either a) coaching quality and mental health or b) diet and mental health—but not both sets—will yield an unbiased estimate of the association between off-field behavior and fantasy points.

13.5.6 Selection Bias

Selection bias occurs when the selection of participants or their inclusion in analyses depends on the variables being studied. For instance, if you are conducting a study on the extent to which sports drink consumption influences fantasy points, there would be selection bias if players are less likely to participate in the study if they score fewer fantasy points.

Now, consider a study in which you conduct a randomized controlled trial (RCT; i.e., an experiment) to evaluate the effect of a new medication on player performance. You randomly assign some players to take the medication and other players to take a placebo. Assume the new medication has side effects and leads many of the players who take it to drop out of the study. This is an example of attrition bias (i.e., systematic attrition). If you were to exclude these individuals from your analysis, it may make it appear that the medication led to better performance, because the players who experienced the side effect (and worse performance) dropped out of the study. Hence, conducting an analysis that excludes these players from the analysis would involve selection bias.

13.6 Conclusion

There are three criteria for establishing causality: 1) the cause precedes the effect. 2) The cause is related to the effect. 3) There are no other alternative explanations for the effect apart from the cause. In general, it is important to be aware of the counterfactual and to consider what would have happened if the supposed cause had not occurred. Various experimental and quasi-experimental designs and approaches can be leveraged to more closely approximate causal inferences. Longitudinal designs, within-subject analyses, inclusion of control variables, and genetically informed designs are all quasi-experimental designs that afford the researcher greater control over some possible third variable confounds. Causal diagrams can be a useful tool for identifying the proper variables to control for (and those not to control for). When confounding exists, it is important to control for the confound(s). It is important not to control for mediators when interested in the total effect of the predictor variable on the outcome variable. In addition, it is important not to control for descendants of the outcome variable. When there is a collision, it is important not to control for the collider (unless the collider is also a confound).

13.7 Session Info

Code
sessionInfo()
R version 4.4.2 (2024-10-31)
Platform: x86_64-pc-linux-gnu
Running under: Ubuntu 24.04.1 LTS

Matrix products: default
BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so;  LAPACK version 3.12.0

locale:
 [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
 [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
 [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
[10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   

time zone: UTC
tzcode source: system (glibc)

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
[1] ggdag_0.2.13  dagitty_0.3-4

loaded via a namespace (and not attached):
 [1] viridis_0.6.5      generics_0.1.3     tidyr_1.3.1        stringi_1.8.4     
 [5] digest_0.6.37      magrittr_2.0.3     evaluate_1.0.1     grid_4.4.2        
 [9] fastmap_1.2.0      jsonlite_1.8.9     ggrepel_0.9.6      gridExtra_2.3     
[13] purrr_1.0.2        viridisLite_0.4.2  scales_1.3.0       tweenr_2.0.3      
[17] cli_3.6.3          rlang_1.1.4        graphlayouts_1.2.1 polyclip_1.10-7   
[21] tidygraph_1.3.1    munsell_0.5.1      withr_3.0.2        cachem_1.1.0      
[25] yaml_2.3.10        tools_4.4.2        memoise_2.0.1      dplyr_1.1.4       
[29] colorspace_2.1-1   ggplot2_3.5.1      boot_1.3-31        curl_6.0.1        
[33] vctrs_0.6.5        R6_2.5.1           lifecycle_1.0.4    stringr_1.5.1     
[37] V8_6.0.0           htmlwidgets_1.6.4  MASS_7.3-61        ggraph_2.2.1      
[41] pkgconfig_2.0.3    pillar_1.10.0      gtable_0.3.6       glue_1.8.0        
[45] Rcpp_1.0.13-1      ggforce_0.4.2      xfun_0.49          tibble_3.2.1      
[49] tidyselect_1.2.1   knitr_1.49         farver_2.1.2       htmltools_0.5.8.1 
[53] igraph_2.1.2       labeling_0.4.3     rmarkdown_2.29     compiler_4.4.2

Feedback

Please consider providing feedback about this textbook, so that I can make it as helpful as possible. You can provide feedback at the following link: https://forms.gle/LsnVKwqmS1VuxWD18

Email Notification

The online version of this book will remain open access. If you want to know when the print version of the book is for sale, enter your email below so I can let you know.